论文阅读笔记：Ultra-Scalable Spectral Clustering and Ensemble Clustering

最新推荐文章于 2022-10-25 19:26:41 发布

塔_Tass

最新推荐文章于 2022-10-25 19:26:41 发布

阅读量561

点赞数

文章标签：论文阅读聚类机器学习

本文链接：https://blog.csdn.net/weixin_44876302/article/details/127161348

版权

Author: Dong Huang, Chang-Dong Wang, Jian-Sheng Wu, Jian-Huang Lai,
and Chee-Keong Kwoh

摘要

摘要本文重点研究了资源有限的超大规模数据集谱聚类的可扩展性和鲁棒性。提出了两种新的算法，即超可伸缩谱聚类（U-SPEC）和超可伸缩集成聚类（U-SENC）。在U-SPEC中，针对稀疏亲和子矩阵的构造，提出了一种混合代表选择策略和K近邻表示的快速逼近方法。通过将稀疏子矩阵解释为一个二部图，然后利用转移割(transfer cut)对该图进行有效划分，并获得聚类结果。在U-SENC中，多个U-SPEC聚类器进一步集成到集成聚类框架中，以增强U-SPEC的鲁棒性，同时保持高效。基于多个U-SEPC的集成生成，在对象和基簇之间构造一个新的二部图，然后有效地进行分区，以获得一致的聚类结果。值得注意的是，U-SPEC和U-SENC都具有近似线性的时间和空间复杂度，并且能够在具有64 GB内存的PC上对千万级非线性可分离数据集进行稳健高效的聚类。在各种大规模数据集上的实验证明了我们算法的可扩展性和鲁棒性。MATLAB代码和实验数据在

https://www.researchgate.net/publication/330760669

简介

聚类是数据挖掘和机器学习领域的一个基本问题，其目的是将一组对象划分为若干个同类组，每个组称为一个簇。在已经开发的大量聚类算法中，谱聚类由于其在处理非线性可分离数据集方面的良好能力，近年来受到了越来越多的关注。然而，传统谱聚类的一个关键限制在于其巨大的时间和空间复杂性，这严重限制了其在大规模问题中的应用。传统的谱聚类通常包括两个时间和内存消耗阶段，即Affinity矩阵构造和特征分解。通常需要 $\mathcal O(N^2d)$ 时间和 $\mathcal O(N^2)$ 内存来构造亲和矩阵，并需要 $\mathcal O(N^3)$ 时间和 $\mathcal O(N^2)$ 内存来解决特征分解问题，其中N是数据大小，d是维数。随着数据大小N的增加，谱聚类的计算负担急剧增加。例如，给定一个包含100万个对象的数据集，仅保存亲和矩阵就将消耗7450.58 GB内存（矩阵中的每个条目都存储为双精度值），这远远超出了通用机器的内存容量，更不用说特征分解的下一阶段了。

为了减轻谱聚类的巨大计算负担，常用的策略是稀疏化的亲和矩阵，并通过一些稀疏特征solver解决特征分解问题。矩阵稀疏化策略可以减少存储亲和矩阵的内存开销，方便特征分解，但仍需要计算原始亲和矩阵中的所有条目。除了矩阵稀疏化之外，另一种广泛研究的策略是基于子矩阵构造。Nystrom方法从原始数据集中随机选择p个代表（锚点），并构建 $N x p$ 的亲和子矩阵。Cai等人扩展了Nystrom方法并提出了基于锚点的谱聚类（LSC）方法，该方法对数据集执行k-means，以获得p个聚类中心作为p个代表。然而，这些基于子矩阵的谱聚类方法通常受到 $\mathcal O(Np)$ 复杂性瓶颈的限制，这是它们处理超大规模数据集的关键障碍，因为为了获得更优的近似值需要更大的p。此外这种代表的选择是一次性的，这给聚类的鲁棒性带来不稳定的因素。

有鉴于此，本文重点关注对于超大规模数据集的谱聚类可伸缩性和健壮性。在U-SPEC中，提出了一种新的混合代表选择策略有效地找到p代表，这减少了基于k-means选择的时间复杂度。然后，设计了一种K近邻表示的快速近似方法，以有效地构造具有 $\mathcal O(Np^{1/2}d)$ 时间和 $\mathcal O(Np^{1/2})$ 内存的稀疏子矩阵。以稀疏子矩阵作为交叉亲和矩阵，在数据集和代表集之间构造一个二部图。通过利用二部图结构，转移割被用来解决需要 $\mathcal O(NK(K+k)p^3)$ 时间的特征分解问题，其中k是类簇数，K是最近代表数。最后，采用k-means离散化方法从一组k个特征向量构造聚类结果，所需时间为 $\mathcal O(Nk^2t)$ 。一般地由于k和K远小于N，我们的U-SPEC算法的时间和空间复杂度分别由 $\mathcal O(Np^{1/2}d)$ 和 $\mathcal O(Np^{1/2})$ 主导。

此外，为了超越U-SPEC的一次性近似并提供更好的聚类鲁棒性，通过将多个U-SPEC聚类器集成到一个统一的集成聚类框架中，提出了U-SENC算法。在十个大型数据集（包括五个合成数据集和五个真实数据集）上进行了广泛的实验，结果表明，我们的U-SPEC和U-SENC算法在聚类鲁棒性和可扩展性方面都优于最先进的算法。

2 相关工作

2.1 可伸缩谱聚类

为了避免计算全亲和矩阵，基于子矩阵的近似已成为谱聚类的一个强大而有效的工具。Nystrom近似从数据集中随机选择p代表，并在N个对象和p个代表之间构建 $N\times p$ 的亲和子矩阵。

尽管随机代表选择非常有效，但就所选代表的质量而言，它通常是不稳定的。此外，虽然已经表明，较大的p通常有利于更好的近似，但在处理非常大的数据集时，子矩阵构造的内存成本仍然是一个关键瓶颈。为了解决随机选择的潜在不稳定性，Cai和Chen提出了LSC算法，该算法首先通过k-means将数据集划分为p个簇，然后以p个簇中心为代表。随着 $N\times p$ 子矩阵的构造，他们通过保留每行的K个最近代表并将其他的归零来进一步稀疏化。尽管与以前的方法相比取得了进步，LSC算法仍然存在三个计算瓶颈[4]。首先，尽管基于k-means的选择通常提供了一组更好的代表，但它在稀疏化之前，仍然需要计算 $N\times p$ 子矩阵中所有可能的项。

最近，He等人[5]没有使用p代表，而是使用傅里叶特征来表示核空间中的数据对象，并在N个对象和p个选定的傅里叶特性之间建立 $N\times p$ 子矩阵，在此基础上可以执行有效的特征分解。通过结合新设计的正Euler核，Wu等人提出了Euler谱聚类（EulerSC）方法，并证明了EulerSC等价于加权正Euler k-means。然而，EulerSC只能使用正的Euler核来定义成对相似性，对于具有其他相似性度量的一般谱聚类公式是不可行的。此外，它的聚类鲁棒性很大程度上依赖于正确选择Euler核参数，如果没有先验知识很难找到。

2.2 集成聚类

集合聚类是近年来流行的一种技术，其目的是将多个基本聚类组合成更好、更健壮的一致聚类。略，有兴趣请移步原文。

3. 框架

3.1 超可伸缩谱聚类 U-SPEC

第一步：我们提出了一种混合表示学习，在随机选择表示的高速性和使用k-means的有效性之间取得平衡。
第二步：我们开发了一种从粗到细的方法来有效地逼近每个数据对象的K最近邻表示，并在N个对象和p个代表之间构造一个稀疏的亲和子矩阵
第三步：这样的Nxp亲和度矩阵被看作一个二部图（bipartite），然后有效地进行分区

3.1.1 混合表示学习

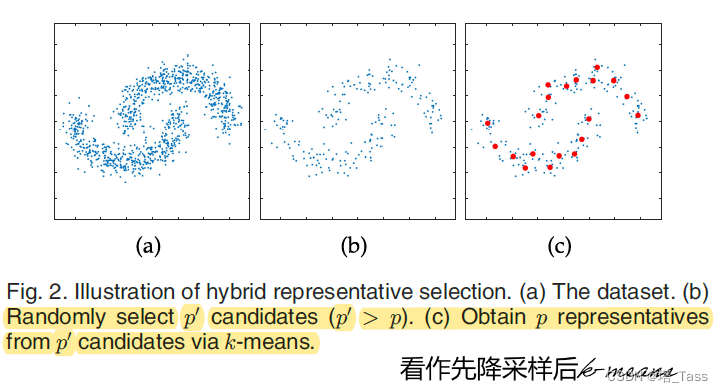
首先随机采样 $p^{'}$ 个候选点，其中 $p^{'}$ 远小于N，但是大于所需的p个代表，如 $p^{'} = 10 p$ 。然后对这 $p^{'}$ 个候选点进行k-means来获得p个cluster，并把聚类中心作为这p个代表。于是计算复杂度由 $\mathcal O(Npdt)$ 降为 $\mathcal O(p'pdt)$ ，如图1所示：

注意这里的p可不是真实的聚类数目，而是需要的代表个数！

在这里插入图片描述

3.1.2 对K近邻代表的近似

由第一步得到了p个最具有代表性的点。接下来是计算所有N个点和这p个代表集合之间的pair-wise相似性。尽管p很小，如取1000个点，但当N很大时，计算这样一个 $N\times p$ 的亲和度矩阵依然是开销很大的。

我们很自然可以想到取每个点的topK近邻，然后转化为稀疏矩阵，用稀疏特征求解器来计算特征值分解。但是注意到，所谓K近邻本质上就是取每一行最大的K个元素，但是所有个 $N\times p$ 的亲和度元素依然是要计算的。如在1000个代表中取5近邻的时候，只有0.5%的最大的元素是有效的，而剩下99.5%的元素是要被置零的，也就是说99.5%的时间和内存被浪费用来计算那些不会被用到的相似度！

与传统的K-NN近似场景不同，该场景主要处理具有 $N\times N$ 亲和矩阵的一般图，而我们是在具有 $N\times p$ 亲和子矩阵的严重不平衡二部图中找到K-最近邻。这种不平衡性对我们的K-最近代表近似问题至关重要。一方面，它使得传统的K-NN近似方法在这里不合适。另一方面，它也可能有助于设计我们的K最近代表逼近策略。具体来说，我们提出了一种由粗到细的策略，如下图：

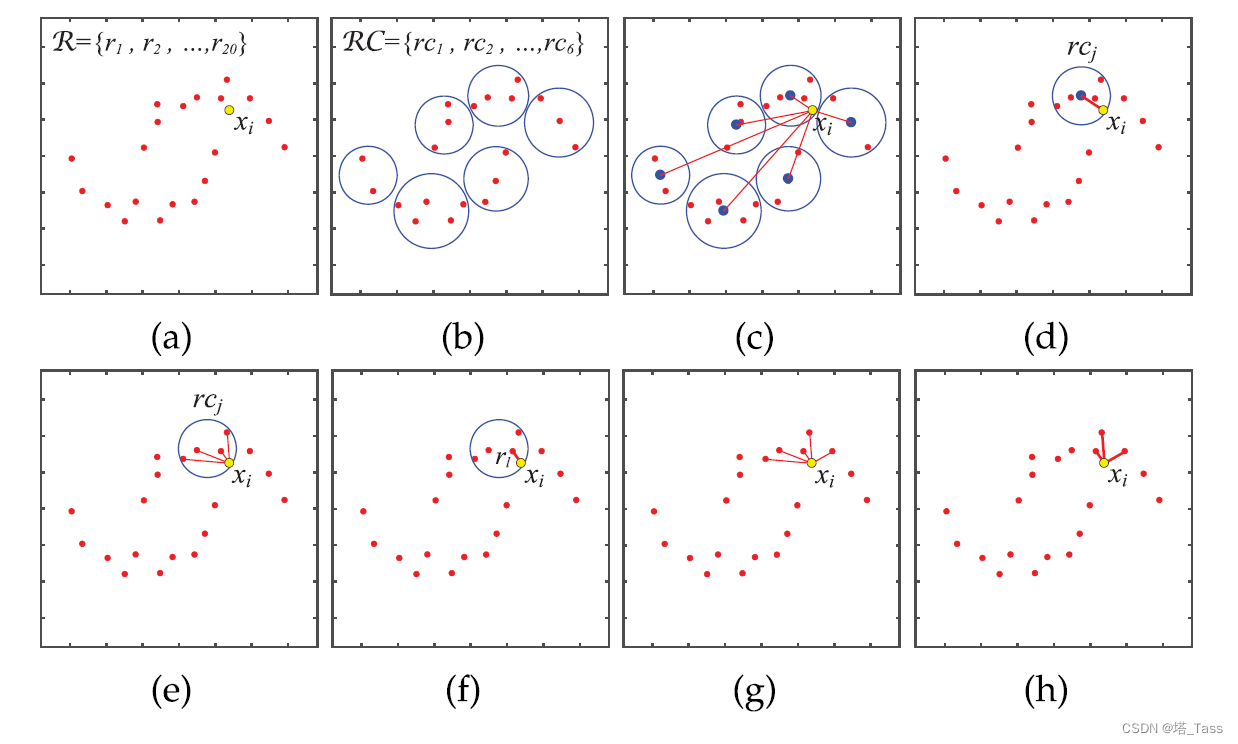
在这里插入图片描述
a) 给定20个代表和来自原始数据集的点 $x_i$
b) 将20个代表划分为6个粗粒度代表类簇（如使用k-means）
c) 计算 $x_i$ 和这六个类簇的聚类中心的距离。
d) 得到离聚类中心距离最近的那个类簇 $rc_j$
e) 再计算该类簇中所有点中离 $x_i$ 的距离
f) 取得最近的代表 $r_l$
g) 计算 $r_l$ 的K’个最近邻，K’>K
h) 计算 $x_i$ 和这K’个点之间的距离，然后从K’中取最近的K个点。

这样一来，我们需要储存和计算的点对相似度信息大大减少了。

3.1.3 二部图划分

亲和子矩阵 $B$ 反映了数据 $\mathcal X$ 与代表 $\mathcal R$ 之间的关系，可以自然地解释为二部图 $G=\{\mathcal X, \mathcal R, B\}$ ，那么 $\mathcal X$ 就是是节点集，B是交叉亲和矩阵（如图4所示）。通过利用二部图结构，transfer cut可以用于有效地划分图并获得最终聚类结果。
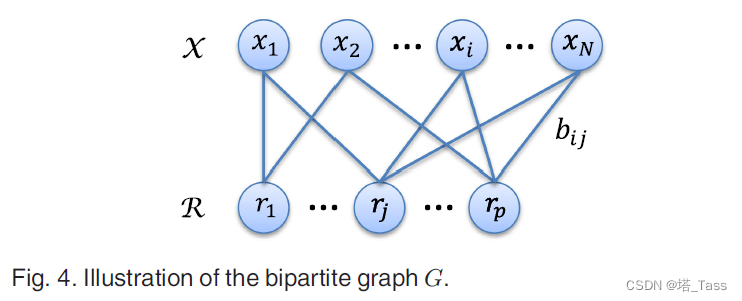
在这里插入图片描述
假如我们把图G看作具有N+p个节点的一般图，那么整个affinity矩阵可以写作：

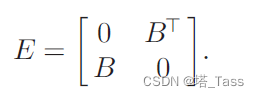
那么谱聚类求解该问题的方法为：
$Lu=\gamma D u \quad\quad (1)$
其中L为E的图拉普拉斯，D为E的 $N + p$ 维度矩阵。通过利用二部结构，我们借助transfer cut将图 $G$ （具有 $N + p$ 个节点）上的特征问题方程（8）简化为更小图 $G_\mathcal R$ （具有 $p$ 个节点）的特征问题。具体来说，图GR被构造为 $G_\mathcal R=\{\mathcal R, E_\mathcal R\}$ ，其中 $\mathcal R$ 是代表节点子集， $E_\mathcal R = B^\top D_\mathcal X^{-1}B$ 是亲和矩阵（其计算需要 $\mathcal O(NK^2)$ 时间），度矩阵 $D_\mathcal X \in \mathbb R^{n\times n}$ 是一个对角阵，第i项为B第i行的和（B是Nxp维的）。于是，在图 $G_\mathcal R$ 上的广义本征问题可以表示为
$L_\mathcal Rv=\lambda D_\mathcal R v \quad\quad (2)$

其中 $\lambda$ 和 $v$ 为特征值和特征向量。已有论文证明了求解公式1和2是等价的。假设求解1得到的topk个最小特征值及其对应的特征向量 $\{\gamma_i, u_i\}^k_{i=1}$ 和求解2得到的 $\{\lambda_i, v_i\}^k_{i=1}$ ，有：
$\gamma_i(2-\gamma_i) =\lambda_i$
$u_i=\left[\begin{array}{l} h_i \\ v_i \end{array} \right], h_i = \frac{1}{1-\gamma_i}Tv_i \quad \quad(3)$
其中 $T=D^{-1}_\mathcal X B$ 为转移概率矩阵。这样一来，只需要计算公式2的特征分解就可以得到所需的特征向量 $u_i$ ，计算复杂度为 $\mathcal O(p^3)$ 。

总共的计算复杂度：
计算亲和矩阵 $E_\mathcal R$ 需要 $O(NK^2)$ ，计算 $E_\mathcal R$ 上的特征分解需要 $\mathcal O(p^3)$ ，由 $v_i$ 作公式3的变换需要k次$ $\mathcal O(NK)$ ，即 $\mathcal O(NKk)$ ，总计为 $\mathcal O(NK(K+k)+p^3)$

3.2 超可伸缩集成聚类 U-SENC

将多个超可伸缩谱聚类 U-SPEC进行集成，略。

4. 实验

4.1 数据集

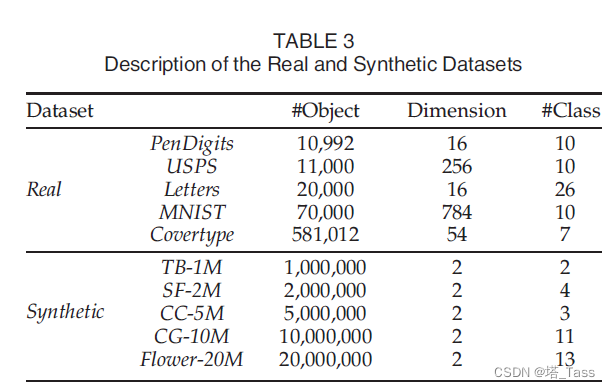
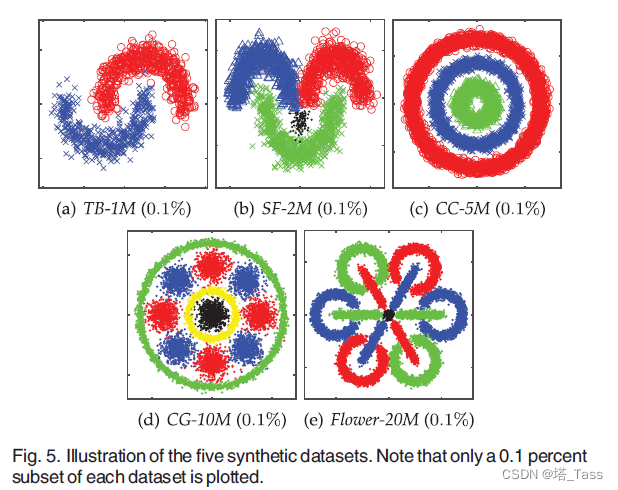
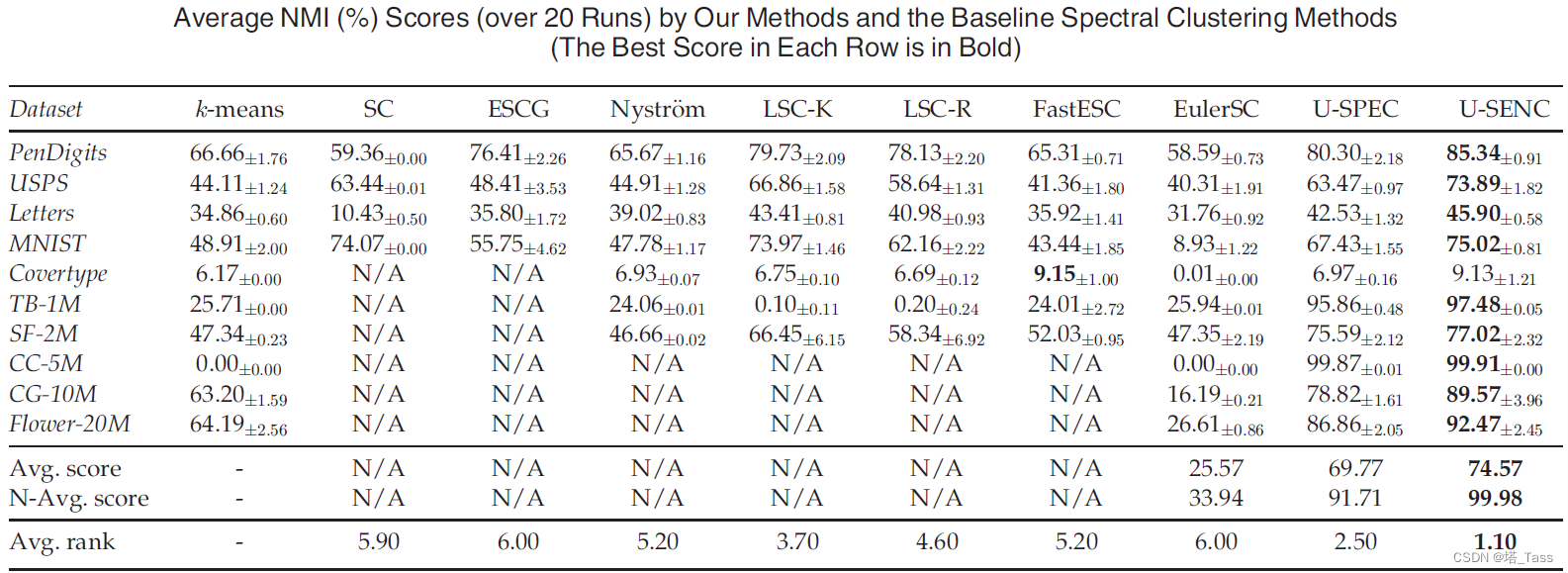
在这里插入图片描述

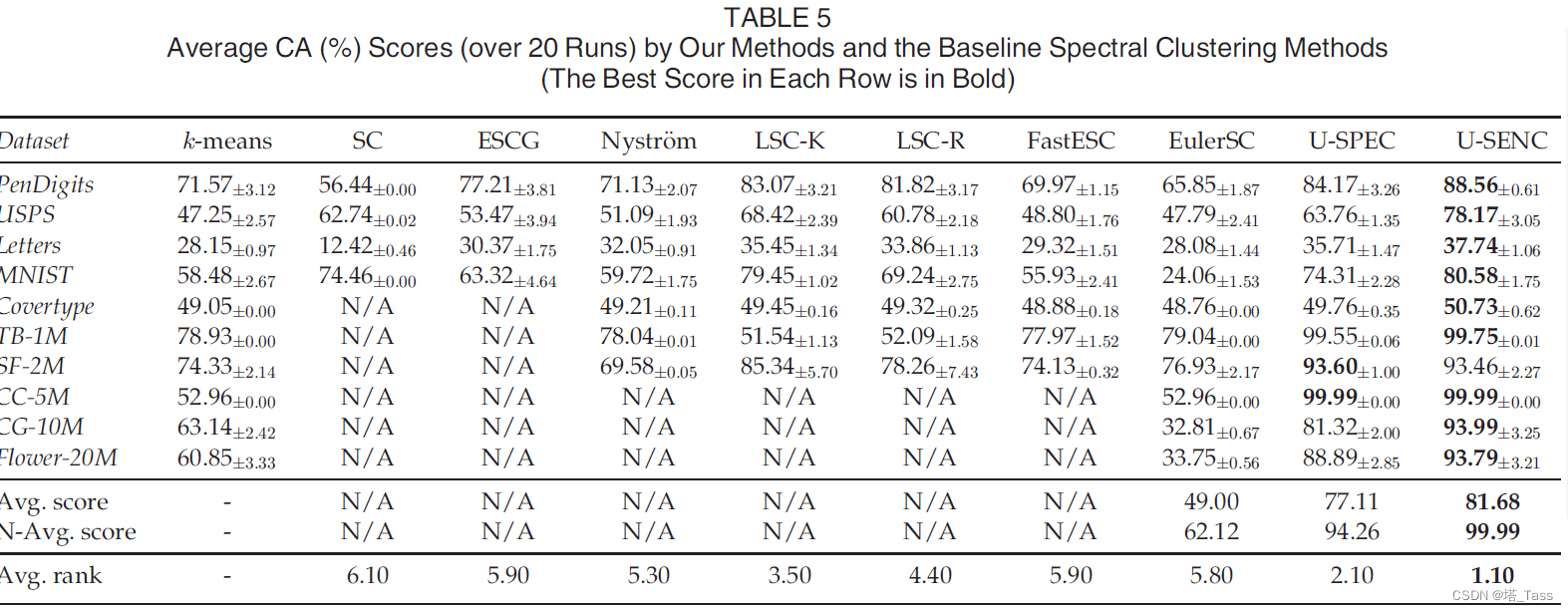
ACC & NMI

在这里插入图片描述

Time Cost

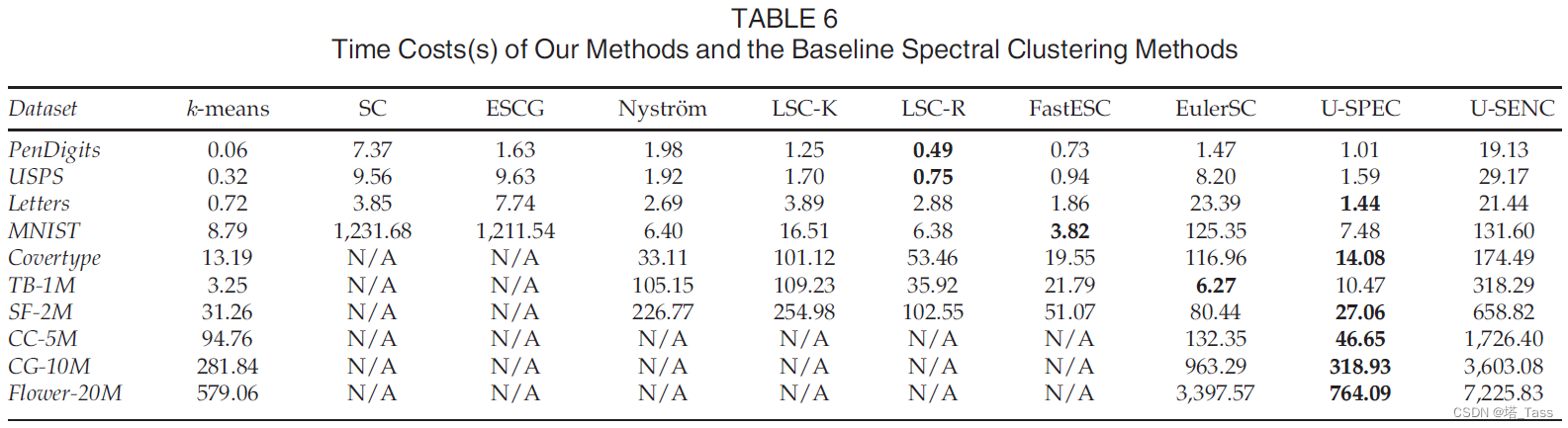
在这里插入图片描述

Number of Representative $p$

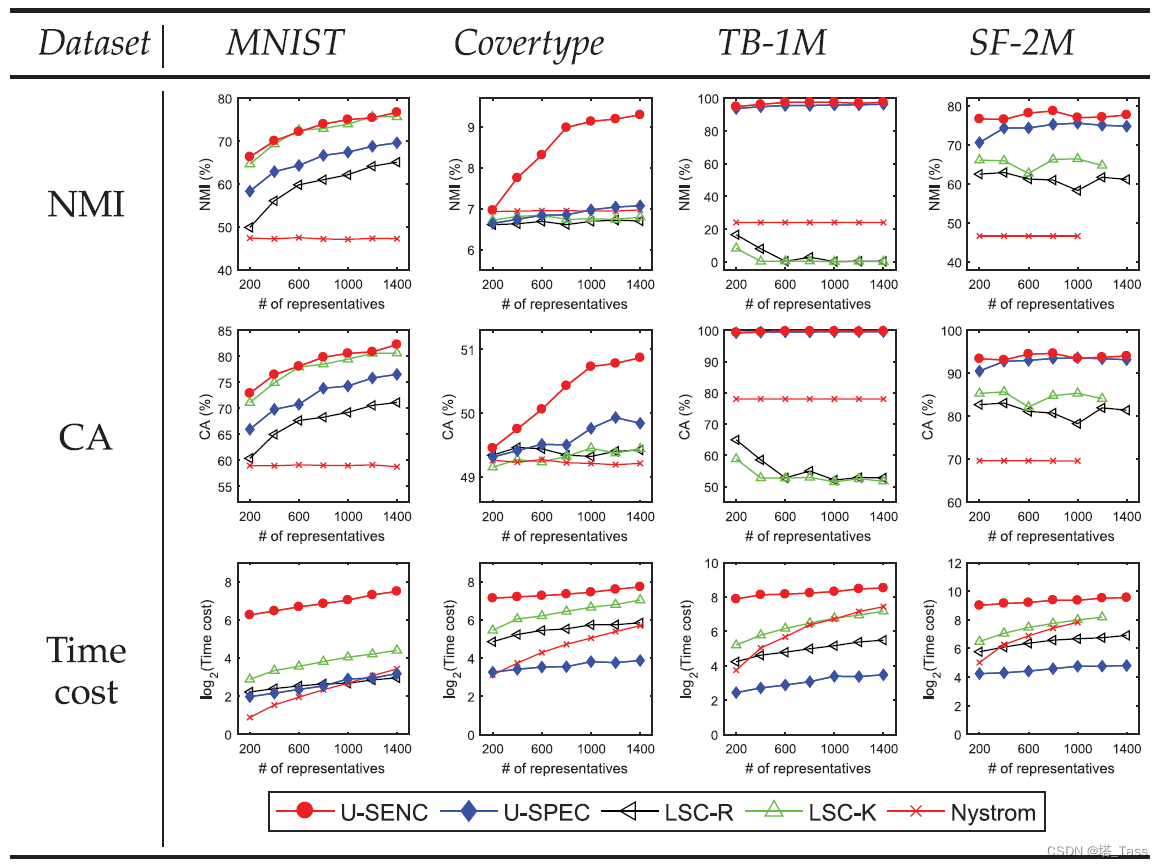
在这里插入图片描述

Number of Nearest Neighbors $K$

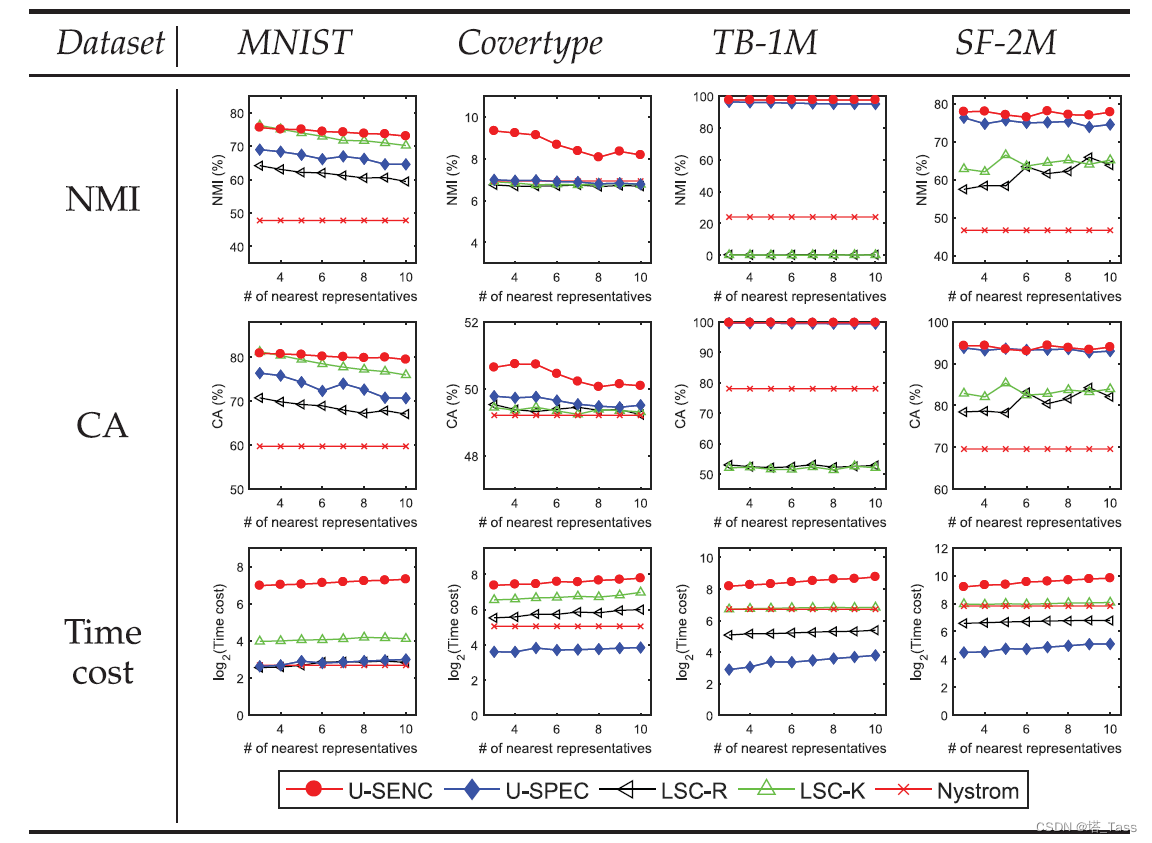
在这里插入图片描述

波动情况

在这里插入图片描述

塔_Tass

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
1
评论
论文阅读笔记：Ultra-Scalable Spectral Clustering and Ensemble Clustering

本文重点研究了资源有限的超大规模数据集谱聚类的可扩展性和鲁棒性。提出了两种新的算法，即超可伸缩谱聚类（U-SPEC）和超可伸缩集成聚类（U-SENC）。在U-SPEC中，针对稀疏亲和子矩阵的构造，提出了一种混合代表选择策略和K近邻表示的快速逼近方法。通过将稀疏子矩阵解释为一个二部图，然后利用转移割(transfer cut)对该图进行有效划分，并获得聚类结果。在U-SENC中，多个U-SPEC聚类器进一步集成到集成聚类框架中，以增强U-SPEC的鲁棒性，同时保持高效。
复制链接

扫一扫