网络结构
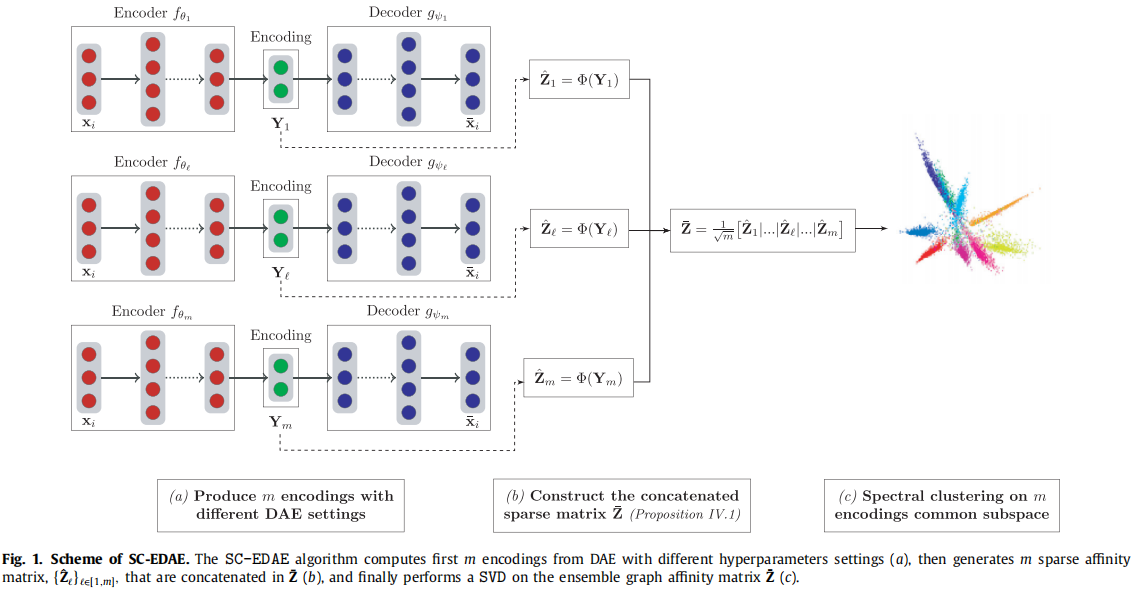
给定数据矩阵
X
∈
R
n
×
d
X \in R^{n×d}
X∈Rn×d,首先使用
m
m
m个不同超参数的AutoEncoder(由PCA构建)进行训练,得到中间层表示
{
Y
l
}
l
∈
[
1
,
m
]
\{Y_l \}_{l \in [1, m]}
{Yl}l∈[1,m]。然后通过每个
Y
l
Y_l
Yl构造一个图相似度矩阵
S
l
S_l
Sl并将其融合成一个集成的图相似矩阵
S
ˉ
\bar S
Sˉ。最后,在
S
ˉ
\bar S
Sˉ上应用谱聚类方法。
接下来我们从谱聚类切入,详细介绍相似矩阵的构建过程。
谱聚类
这里使用的是对称拉普拉斯矩阵。
L
s
y
m
=
D
−
1
/
2
L
D
−
1
/
2
=
I
−
D
−
1
/
2
W
D
−
1
/
2
L_{sym} =D^{−1/2}LD^{−1/2} = I - D^{−1/2}WD^{−1/2}
Lsym=D−1/2LD−1/2=I−D−1/2WD−1/2
对于无向图 G G G的切图,我们的目标是将图 G ( V , E ) G(V,E) G(V,E)切成相互没有连接的k个子图,每个子图点的集合为: A 1 , A 2 , . . . , A k A_1,A_2,...,A_k A1,A2,...,Ak,它们满足 A i ∩ A j = ∅ A_i∩A_j=∅ Ai∩Aj=∅,且 A 1 ∪ A 2 ∪ . . . ∪ A k = V A_1∪A_2∪...∪A_k=V A1∪A2∪...∪Ak=V.
对于任意两个子图点的集合
A
,
B
⊂
V
,
A
∩
B
=
∅
A,B⊂V, A∩B=∅
A,B⊂V,A∩B=∅, 我们定义
A
A
A和
B
B
B之间的切图权重为:
W
(
A
,
B
)
=
∑
i
∈
A
,
j
∈
B
w
i
j
W(A, B) = \sum\limits_{i \in A, j \in B}w_{ij}
W(A,B)=i∈A,j∈B∑wij
那么对于我们
k
k
k个子图点的集合:
A
1
,
A
2
,
.
.
.
,
A
k
A_1,A_2,...,A_k
A1,A2,...,Ak,我们定义切图cut为:
c
u
t
(
A
1
,
A
2
,
.
.
.
A
k
)
=
1
2
∑
i
=
1
k
W
(
A
i
,
A
‾
i
)
cut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}W(A_i, \overline{A}_i )
cut(A1,A2,...Ak)=21i=1∑kW(Ai,Ai)
其中 A ˉ i \bar A_i Aˉi为 A i A_i Ai的补集,意为除 A i A_i Ai子集外其他 V V V的子集的并集。
那么如何切图可以让子图内的点权重和高,子图间的点权重和低呢?一个自然的想法就是最小化
c
u
t
(
A
1
,
A
2
,
.
.
.
,
A
k
)
cut(A_1,A_2,...,A_k)
cut(A1,A2,...,Ak), 但是可以发现,这种极小化的切图存在问题,如下图
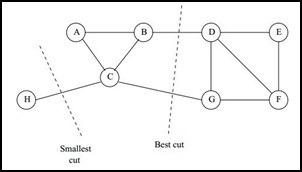
我们选择一个权重最小的边缘的点,比如C和H之间进行cut,这样可以最小化
c
u
t
(
A
1
,
A
2
,
.
.
.
,
A
k
)
cut(A_1,A_2,...,A_k)
cut(A1,A2,...,Ak), 但是却不是最优的切图,如何避免这种切图,并且找到类似图中"Best Cut"这样的最优切图呢,可以用下面的Ncut的切图方法。
Ncut切图
对每个切图,不光考虑最小化cut(A1,A2,…Ak),它还同时考虑最大化每个子图点的权重
N
C
u
t
(
A
1
,
A
2
,
.
.
.
A
k
)
=
1
2
∑
i
=
1
k
W
(
A
i
,
A
‾
i
)
v
o
l
(
A
i
)
NCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i )}{vol(A_i)}
NCut(A1,A2,...Ak)=21i=1∑kvol(Ai)W(Ai,Ai)
那么怎么最小化这个Ncut函数呢?牛人们发现,Ncut函数可以通过如下方式表示。
我们引入指示向量
h
j
∈
{
h
1
,
h
2
,
.
.
.
,
h
k
}
h_j∈\{h_1,h_2,...,h_k\}
hj∈{h1,h2,...,hk},
j
=
1
,
2
,
.
.
.
k
,
j=1,2,...k,
j=1,2,...k,对于任意一个向量
h
j
h_j
hj, 它是一个n维向量(n为样本数),我们定义
h
i
j
h_{ij}
hij为:
h
i
j
=
{
0
v
i
∉
A
j
1
v
o
l
(
A
j
)
v
i
∈
A
j
h_{ij}= \begin{cases} 0& { v_i \notin A_j}\\ \frac{1}{\sqrt{vol(A_j)}}& { v_i \in A_j} \end{cases}
hij={0vol(Aj)1vi∈/Ajvi∈Aj
那么我们对于
h
i
T
L
h
i
h_i^TLh_i
hiTLhi,我们有
 我们的优化目标是
我们的优化目标是
N
C
u
t
(
A
1
,
A
2
,
.
.
.
A
k
)
=
∑
i
=
1
k
h
i
T
L
h
i
=
∑
i
=
1
k
(
H
T
L
H
)
i
i
=
t
r
(
H
T
L
H
)
NCut(A_1,A_2,...A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = tr(H^TLH)
NCut(A1,A2,...Ak)=i=1∑khiTLhi=i=1∑k(HTLH)ii=tr(HTLH)
但是此时我们的
H
T
H
≠
I
H^TH \neq I
HTH=I,而是
H
T
D
H
=
I
H^TDH = I
HTDH=I。推导如下:
h
i
T
D
h
i
=
∑
j
=
1
n
h
i
j
2
d
j
=
1
v
o
l
(
A
i
)
∑
j
∈
A
i
d
j
=
1
v
o
l
(
A
i
)
v
o
l
(
A
i
)
=
1
h_i^TDh_i = \sum\limits_{j=1}^{n}h_{ij}^2d_j =\frac{1}{vol(A_i)}\sum\limits_{j \in A_i}d_j= \frac{1}{vol(A_i)}vol(A_i) =1
hiTDhi=j=1∑nhij2dj=vol(Ai)1j∈Ai∑dj=vol(Ai)1vol(Ai)=1
也就是说,此时我们的优化目标最终为
a
r
g
m
i
n
⏟
H
t
r
(
H
T
L
H
)
s
.
t
.
H
T
D
H
=
I
\underbrace{arg\;min}_H\; tr(H^TLH) \;\; s.t.\;H^TDH=I
H
argmintr(HTLH)s.t.HTDH=I
此时我们的H中的指示向量h并不是标准正交基,所以将指示向量矩阵H做一个小小的转化。
我们令
H
=
D
−
1
/
2
F
H = D^{-1/2}F
H=D−1/2F,则
H
T
L
H
=
F
T
D
−
1
/
2
L
D
−
1
/
2
F
,
H
T
D
H
=
F
T
F
=
I
H^TLH = F^TD^{-1/2}LD^{-1/2}F, H^TDH=F^TF = I
HTLH=FTD−1/2LD−1/2F,HTDH=FTF=I,也就是说优化目标变成了:
a
r
g
m
i
n
⏟
F
t
r
(
F
T
D
−
1
/
2
L
D
−
1
/
2
F
)
s
.
t
.
F
T
F
=
I
\underbrace{arg\;min}_F\; tr(F^TD^{-1/2}LD^{-1/2}F) \;\; s.t.\;F^TF=I
F
argmintr(FTD−1/2LD−1/2F)s.t.FTF=I
求出
D
−
1
/
2
L
D
−
1
/
2
D^{-1/2}LD^{-1/2}
D−1/2LD−1/2的最小的前
k
k
k个特征值,然后求出对应的特征向量,并标准化,得到最后的特征矩阵
F
F
F,最后对F进行一次传统的聚类(比如K-Means)即可。
一般来说,
D
−
1
/
2
L
D
−
1
/
2
D^{-1/2}LD^{-1/2}
D−1/2LD−1/2相当于对拉普拉斯矩阵L做了一次标准化,即
L
i
j
d
i
∗
d
j
\frac{L_{ij}}{\sqrt{d_i*d_j}}
di∗djLij。
回归本文
L
s
y
m
=
D
−
1
/
2
L
D
−
1
/
2
=
I
−
D
−
1
/
2
W
D
−
1
/
2
L_{sym} =D^{−1/2}LD^{−1/2} = I - D^{−1/2}WD^{−1/2}
Lsym=D−1/2LD−1/2=I−D−1/2WD−1/2
最小化
L
s
y
m
L_{sym}
Lsym就是最大化
D
−
1
/
2
W
D
−
1
/
2
D^{−1/2}WD^{−1/2}
D−1/2WD−1/2

(1)的解是S的最大k个特征值,B是其对应的最大k个特征向量,对B的每一行进行归一化后再使用K-means分类。
构建邻接矩阵
使用Landmark 和AnchorGraph的思想对原始的n个表示进行了转换。
利用K-Means选取p个点作为landmark;计算landmark与剩余数据之间相似度矩阵Z,用p线性表示n个数据。
邻接矩阵
S
l
S_l
Sl用
Z
l
Z_l
Zl表示:
S
l
=
Z
l
Λ
−
1
Z
l
T
Λ
=
∑
i
=
1
n
Z
i
j
l
S_l = Z_l \Lambda ^{-1} Z_l^T \\ \Lambda = \sum^n_{ i=1} Z^l_{ij}
Sl=ZlΛ−1ZlTΛ=i=1∑nZijl
进一步表示:

最终整体的方式采用多个亲和度矩阵平均的方法: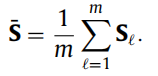
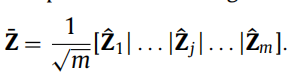
优化算法
不直接求B对应的最大k个特征向量,而是求U
最小化
∣
∣
Z
−
B
B
T
Z
∣
∣
F
2
||Z − BB^TZ||^2_F
∣∣Z−BBTZ∣∣F2,就是最大化
∣
∣
B
B
T
Z
∣
∣
F
2
||BB^TZ||^2_F
∣∣BBTZ∣∣F2,根据
∣
∣
M
∣
∣
F
2
=
T
r
[
M
T
M
]
||M||^2_F=Tr[M^TM]
∣∣M∣∣F2=Tr[MTM],
所以
∣
∣
B
B
T
Z
∣
∣
F
2
=
T
r
[
(
B
B
T
Z
)
T
(
B
B
T
Z
)
]
=
T
r
[
Z
T
B
B
T
B
B
T
Z
]
=
T
r
[
Z
T
B
B
T
Z
]
||BB^TZ||^2_F = Tr[(BB^TZ)^T(BB^TZ)] \\ \qquad \qquad \qquad \quad=Tr[Z^TBB^TBB^TZ] \\ \qquad \qquad \qquad \quad=Tr[Z^TBB^TZ]
∣∣BBTZ∣∣F2=Tr[(BBTZ)T(BBTZ)]=Tr[ZTBBTBBTZ]=Tr[ZTBBTZ]
根据
T
r
[
A
B
]
=
T
r
[
B
A
]
Tr[AB]=Tr[BA]
Tr[AB]=Tr[BA] 得到
T
r
[
Z
T
B
B
T
Z
]
=
T
r
[
B
T
Z
Z
T
B
]
Tr[Z^TBB^TZ]=Tr[B^TZZ^TB]
Tr[ZTBBTZ]=Tr[BTZZTB]


参考链接:
Large Scale Spectral Clustering with Landmark-Based Representation (in Julia)
Large Scale Spectral Clustering with Landmark-Based Representation
Large Graph Construction for Scalable Semi-Supervised Learning
谱聚类(spectral clustering)原理总结-刘建平






















 2507
2507











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








