Author:Jeff Z. HaoChen,Colin Wei, Tengyu Ma et.al.
Arxiv: 2106.04156
Stanford University
待写部分为泛化性和误差边界的理论分析
Abstract
最近的自监督学习方面的工作主要依赖对比学习范式:该范式通过正样本对来学习表征,同时保持负对距离很远。尽管经验上取得了成功,但理论基础是有限的——假设正样本对的条件独立,而实际中是高度相关的(即,相同图像的Augmentation)。本工作分析了对比学习,且不需要假设条件独立,使用一个新的概念的增强图(Augmentation graph)。这个图中的边连接了相同数据点的Augmentation,而这些来自增强样本的groud-truth自然地形成了连接的子图。在增强图上执行谱分解的损失可以简洁地等价为神经网络表示上的对比学习目标。最小化这一目标会导致在线性评估下具有可证明的精度保证的特征。
1. Introduction
计算机视觉中的自监督信号通常是通过使用数据增强来产生同一图像的多个视图来定义的,鼓励比随机抽样数据点的增强视图对更紧凑的表示。尽管取得了经验上的成功,但对于为什么自监督学习到的表征可以适应下游任务(如使用线性头)的理论理解有限。最近对比学习的数学分析提供了一个假设,即标签或隐藏变量在某种程度上是有条件独立的。然而,在实际应用来中,来自同一图像的两种增强视图表现出很强的相关性,它们不是独立于标签的。因此,现有的理论似乎并不能解释自监督学习的成功。
本文提出了一个不需要条件独立性假设的理论框架。我们设计了一个有原则的,实际的损失函数来学习神经网络表示,它类似于最先进的对比学习方法。我们所利用的是在同一个类中的总体数据的连续性的概念。虽然来自同一类的随机图像对可能相距很远,但这对图像通常由(许多)自然图像序列连接,其中序列中的连续图像是同一类中的近邻。如图1所示,两只非常不同的法国斗牛犬可以通过一系列法国斗牛犬连接起来(它们可能不在训练集中,但支持种群分布)。之前的工作(Wei et al.,2020)通过经验证明了这种类型的连通性特性,并将其用于伪标记算法的分析。当一个示例的邻域包含许多不同类型的增强时,这个属性就更加显著。
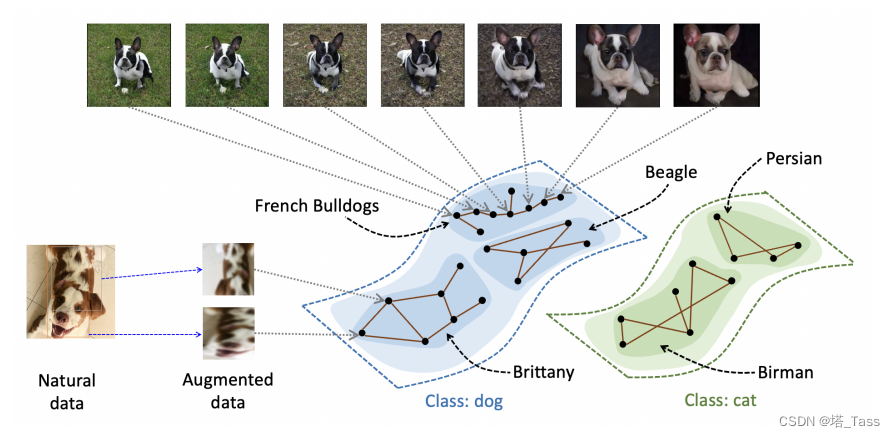
图1(1):如果两个增强数据是同一自然数据点的视图,则会连接它们。在下游任务中,来自不同类的数据增强被假定是几乎断开的,而在同一个类中有更多的连接。我们允许在一个与潜在的子类对应的类中存在不连通的子图。
更正式地,我们定义了population augmentation graph,其顶点都是族群分布中所有的增广样本。如果两个顶点是同一张图像的增广,则它们有一条edge相连。我们的主要假设是,对于一些适当的 m ∈ Z + m∈\mathcal Z^+ m∈Z+,我们不能将图划分为互相有很少连接的 m + 1 m + 1 m+1个子图。换句话说,这直观地说明了在population augmentation graph中最多有 m m m个类簇。这个假设可以看作是关于族群分布的连续性假设的一个图论版本。我们还假设在不同的ground-truth类中只有很少的边连接。图1说明了一个现实的场景,其中狗和猫是真实的类别,它们之间几乎没有edge。每个细粒度类形成一个子图,有足够的内部连通性。
上述假设从不需要基于类的正样本对的独立性,并且可以允许类内断开的子图。下游任务中的类也可以更加灵活,只要它们在augmentation graph中断开连接。例如,当augmentation graph由 m m m个对应于细粒度类的不连通子图组成时,我们的假设允许下游任务将 r ≤ m r≤m r≤m个(包含这些细粒度类的) 粗粒度类作为子分区。之前关于伪标记算法的工作(Wei et al.,2020)基本上需要子图和下游类(即r = m)之间的精确对齐。他们面临着这一限制,因为他们的分析需要在未标记的数据上拟合离散的伪标签。我们避免了这个困难,因为我们考虑直接学习未标记数据上的连续表示。
本文的主要观点是,对比学习可以看作是谱聚类的一种参数化形式。具体地说,假设我们将谱分解或谱聚类用在上定义的邻接矩阵。我们形成一个top-k个特征向量作为列的矩阵,并将矩阵的每一行解释为一个样本的表示(在
R
k
\mathbb R^k
Rk中)。有些令人惊讶的是,我们证明了这个特征提取器也可以通过最小化以下总体目标来恢复(直到一些线性变换),这是标准对比损失的一个变体:
L
(
f
)
=
−
2
⋅
E
x
,
x
+
[
f
(
x
)
⊤
f
(
x
+
)
]
+
E
x
,
x
−
[
(
f
(
x
)
⊤
f
(
x
−
)
)
2
]
\mathcal L(f)=-2\cdot \mathbb E_{x,x^+}[f(x)^\top f(x^+)]+\mathbb E_{x,x^-}[\left(f(x)^\top f(x^-)\right )^2]
L(f)=−2⋅Ex,x+[f(x)⊤f(x+)]+Ex,x−[(f(x)⊤f(x−))2]
其中
x
,
x
+
x,x^+
x,x+是同一数据点的一对增广,(x,x−)是一对独立的随机增广数据,f是从增广数据到
R
k
\mathbb R^k
Rk空间的参数化映射。下图说明了特征向量矩阵和学习到的表示之间的关系。我们称之为种群谱对比损失population spectral contrastive loss。
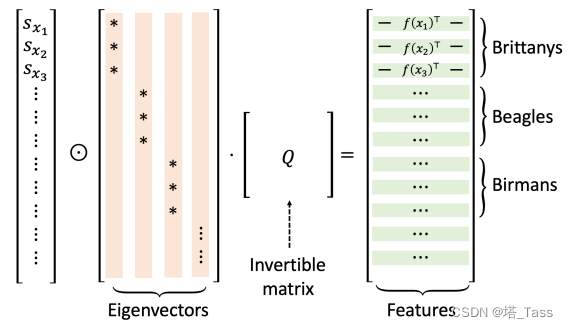
图1(2):对学习到的表征的分解。通过最小化族群谱对比损失学习到的表示(右式的行)可以分解为左式。标量
s
x
i
s_{x_i}
sxi对于每个增强的数据点
x
i
x_i
xi都为正。标记为“特征向量”的矩阵的列是增强图的归一化邻接矩阵的top特征向量。将每个
s
x
i
s_{x_i}
sxi与特征向量矩阵的第
x
x
x行相乘。当类(或子类)在增强图中完全断开时,特征向量是稀疏的,并与子类结构对齐。可逆Q矩阵不影响下游线性评估的性能。
我们的主要结果(定理3.8)表明,当表征维数超过不连通子图的最大数量时,具有学习表示的线性分类保证有一个较小的误差。我们的定理揭示了一个趋势,即当有更多的不连通子图时,需要更大的表示维数。我们的分析依赖于针对线性评估性能的新技术,据我们所知,在谱图理论界尚未对其进行过研究。
谱对比损失也适用于经验数据。我们的方法优化参数化损失函数,因此可以使用现成的泛化边界转换为有限的样本结果。端到端结果(定理4.3)表明,下游标记的样本数量只需要在表示维度(亦即子图总数)上是线性的。这表明对比学习减少了所需的标记例子的数量。
1.1 Contribution
- 受谱分解启发,我们基于族群增强图提出谱对比损失,学习到的表征提供了下游分类保证。
- 我们的分析很容易通过现成的泛化边界适用于具有多项式无标记样本的深度网络。我们的理论框架可以看作是包含两个阶段:我们首先分析使损失最小化的表征,然后研究经验损失,该表征是用一个有界容量的神经网络学习的。
- 我们在标准视觉基准数据集上实现并测试了所提出的谱对比损失。我们的算法很简单,并且不依赖于停止梯度等技巧。
2. Related empirical work
自我监督学习算法已被证明能够成功学习表示有利于下游任务。许多最近的自监督学习算法:
- 通过暹罗网络学习特征,其中两个共享权值的神经网络被应用于增广数据对。
- 在暹罗网络中引入不对称性或使用BYOL,或对SimSiam等暹罗网络的一个分支使用stop gradient,已被证明可以有效地避免特征坍缩。
- 对比方法将InfoNCE损失最小化,即对相同数据的两个视图被吸引,而来自不同数据的视图被拒绝。
3. Spectral contrastive learning on population data
3.1 notation
X ‾ \mathcal {\overline X} X来表示所有原始数据的集合。假设 x ‾ ∈ X ‾ \overline x ∈ \mathcal {\overline X} x∈X属于r个类中的一个, y : X ‾ → [ r ] y: \mathcal {\overline X}→[r] y:X→[r]表示gound-truth标记函数。设 P X ‾ \mathcal P_{\mathcal {\overline X}} PX是 X ‾ \mathcal {\overline X} X上的总体分布,我们从中提取训练数据并测试我们的最终性能。
对于给定 x ‾ ∈ X ‾ \overline x ∈ \mathcal {\overline X} x∈X, 我们用 A ( ⋅ ∣ x ‾ ) \mathcal A(\cdot | \overline x) A(⋅∣x)表示它的增广样本分布。于是, X \mathcal { X} X来表示所有增广数据的集合,他也是所有 A ( ⋅ ∣ x ‾ ) \mathcal A(\cdot | \overline x) A(⋅∣x)支撑集的并集。
我们假设 X ‾ \mathcal {\overline X} X和 X \mathcal {X} X都是有限但指数级大的集合(如,所有 R d \mathbb R^d Rd中的实向量具有有界精度)。我们的理论分析不依赖数据集的大小,但这允许我们使用累和而不是积分。
我们学习特征映射函数
f
:
X
→
R
k
f: \mathcal {X}\rightarrow \mathbb R^k
f:X→Rk, 然后通过使用线性分类器来评估其质量。线性分类器的权值
B
∈
R
k
×
r
B\in\mathbb R^{k\times r}
B∈Rk×r,则预测结果为:
g
f
,
B
(
x
)
=
arg
max
i
∈
[
r
]
(
f
(
x
)
⊤
B
)
i
g_{f,B}(x)=\arg\max_{i\in[r]}\big(f(x)^\top B\big)_i
gf,B(x)=argmaxi∈[r](f(x)⊤B)i。然后,给定一个原始数据样本
X
‾
\mathcal {\overline X}
X,我们对增强数据的预测进行集成,并预测:
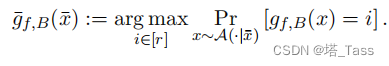
表征和线性头的误差为:
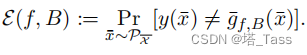
将线性误差定义为该表征可能的最佳线性分类器的误差:
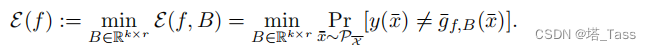
3.2 Augmentation graph and spectral decomposition
我们用增广样本构成的
G
(
X
,
w
)
G(\mathcal X,w)
G(X,w)表示增强图,
w
w
w为定义的边权值。对于任意两个增强数据
x
,
x
′
∈
X
x,x'∈\mathcal X
x,x′∈X,将权重
w
x
x
′
w_{xx'}
wxx′定义为从随机原始数据
x
‾
\overline x
x生成
x
,
x
′
x,x'
x,x′的边际概率:
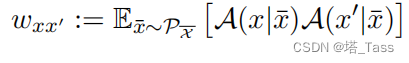
因此,权重之和为1。相对幅度直观地捕捉到了
x
,
x
′
x,x'
x,x′的增广变换之间的接近程度。对于大多数不相关的
x
,
x
′
x,x'
x,x′,
w
x
x
′
w_{xx'}
wxx′的值将显著小于平均值。例如,当
x
x
x和
x
′
x'
x′分别是猫和狗的随机增广时,
w
x
x
′
w_{xx'}
wxx′基本上是零,因为没有哪个自然数据可以
x
‾
\overline x
x同时增强到
x
x
x和
x
′
x'
x′。反之
w
x
x
′
w_{xx'}
wxx′则是非零的,我们说
x
x
x和
x
′
x'
x′有一条边连接。
3.3 一个具有高斯扰动的简化例子。
假设原始数据的支撑流形在欧几里得空间,且数据增广添加的随机噪声采样 N ( 0 , σ 2 ⋅ I d × d ) \mathcal N(0,σ^2\cdot I_{d×d}) N(0,σ2⋅Id×d)的量级远小于原始数据。那么两个增强数据点之间的边的权重接近于零,除非两个数据点的 ℓ 2 \ell_2 ℓ2距离小。因此,所得到的图本质上是欧几里得空间中的 ϵ − b a l l \epsilon-ball ϵ−ball图。
我们将把特征分解应用于 population augmentation graph,然后使用线性分类。记
w
x
=
∑
x
′
∈
X
w
x
x
′
w_x = \sum_{x'\in\mathcal X}w_{xx'}
wx=∑x′∈Xwxx′是与
x
x
x相关的总权值,这通常被视为加权图中
x
x
x的度的模拟。谱图理论中的一个中心对象是归一化邻接矩阵:
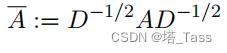
其中,邻接矩阵的元素为
A
x
x
′
=
w
x
x
′
A_{xx'}=w_{xx'}
Axx′=wxx′,度矩阵的对角元素
D
x
x
=
w
x
D_{xx}=w_x
Dxx=wx。
3.4 From spectral decomposition to spectral contrastive learning
我们将把特征向量矩阵
F
∗
F^*
F∗的行参数化为一个神经网络函数,并假设嵌入
u
x
∗
u^∗_x
ux∗可以用
f
(
x
)
∈
F
f(x)\in\mathcal F
f(x)∈F表示,其中
F
\mathcal F
F是包含神经网络的假设类。这允许我们利用神经网络的外推能力,并学习在有限数据集上的表示。
我们采用以下基于矩阵分解的特征向量目标:
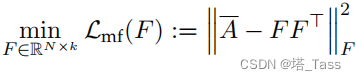
根据经典理论低秩近似,任何最小化
L
m
f
\mathcal L_{mf}
Lmf得到的
F
^
\hat F
F^包含
A
‾
\overline A
A的最大特征向量缩放到正确
F
∗
F^*
F∗的变换——对于一些标准正交矩阵
R
∈
R
k
×
k
R∈\mathbb R^{k\times k}
R∈Rk×k,我们有
F
^
=
F
∗
⋅
d
i
a
g
(
[
γ
1
,
…
,
γ
k
]
)
⋅
R
\hat F= F^∗·diag([\sqrt{γ_1},…,\sqrt{γ_k}])\cdot R
F^=F∗⋅diag([γ1,…,γk])⋅R。幸运的是,将嵌入矩阵乘以右边的任何矩阵和左边的对角矩阵不会改变其线性分类性能,因为线性估计输出的每个维度都被同等地缩放因而不改变
arg
max
\arg\max
argmax的结果。
注意到 u x u_x ux是 F F F的行, F F ⊤ FF^\top FF⊤的每个元素为 u x ⊤ u x u^\top_x u_x ux⊤ux,因此 L m f \mathcal L_{mf} Lmf可以分解成 N 2 N^2 N2个 u x ⊤ u x u^\top_x u_x ux⊤ux之和。有趣的是,如果我们用 w x f ( x ) \sqrt w_x f (x) wxf(x)重参数化每行 u x u_x ux,我们将得到一个非常相似的f损失函数,它类似于实践中使用的对比学习损失,如下引理所示。
Lemma 3.2 (spectral contrasitive loss)
损失函数
L
m
f
\mathcal L_{mf}
Lmf等价于一个特殊的对比学习损失
L
\mathcal L
L和一个加性常数: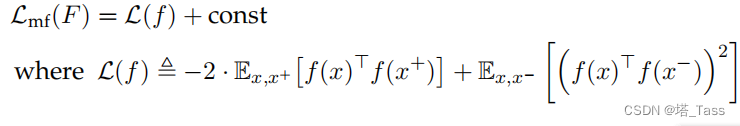
Proof of Lemma 3.2
L
m
f
\mathcal L_{mf}
Lmf可以写成:
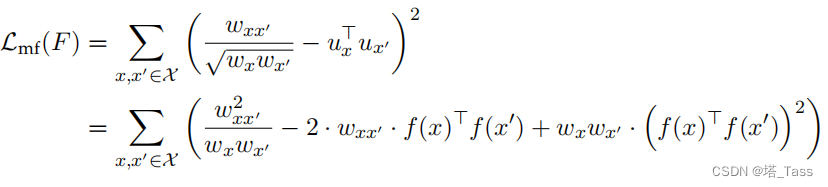
第一项是一个常数,它只依赖于图而不是网络
f
f
f。根据增广图的定义,
w
x
x
′
w_{xx'}
wxx′是随机增广
x
x
x和
x
′
x'
x′为正样本对的概率,而
w
x
w_x
wx是随机增广数据点为
x
x
x的概率。因此,我们可以将方程中最后两项的和重写为引理中的
E
x
,
x
+
\mathbb E_{x,x^+}
Ex,x+和
E
x
,
x
−
\mathbb E_{x,x^-}
Ex,x−。
谱对比损失与许多流行的对比损失相似。例如,SimCLR中的对比损失可以使用简单的代数操作重写为:
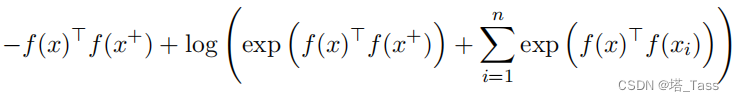
谱对比损失具有与SimCLR相似的经验性能,而不需要大批量的批处理。
3.5 Theoretical guarantees for spectral contrastive loss on population data
为了使 G G G不能被划分为太多的不连通子图的思想形式化,我们引入了狄利克雷电导 (Dirichlet conductance) 和最稀疏m划分 (sparsest m m m-partition) 的概念,这是谱图理论中的标准概念。Dirichlet conductance表示从 S S S到其补集的边的比例:
Definition 3.3 (Dirichlet conductance)
For graph
G
=
(
X
,
w
)
G=(X,w)
G=(X,w) and a subset
S
⊆
X
S ⊆\mathcal X
S⊆X , we define the Dirichlet conductance of
S
S
S as:
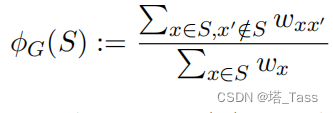 □
\square
□
□
\square
□
当
S
S
S是单例时,根据
w
x
w_x
wx的定义有
ϕ
G
(
S
)
=
1
\phi_G (S) = 1
ϕG(S)=1。对于
i
∈
Z
+
i∈\mathbb Z+
i∈Z+,我们引入sparsest
m
m
m-partition来表示
i
i
i个不相交子集之间的边数。
Definition 3.4 (sparsest
i
i
i-partition)
For
G
=
(
X
,
w
)
G=(X,w)
G=(X,w) and integer
i
∈
[
2
,
∣
X
∣
]
i ∈[2,|X|]
i∈[2,∣X∣], we define the sparsest i-partition as:
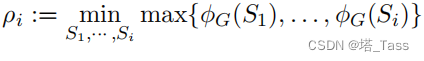
where
S
1
,
⋯
,
S
i
S_1,\cdots, S_i
S1,⋯,Si are non-empty sets that form a partition of
X
\mathcal X
X.
□
\square
□
我们注意到 ρ i ρ_i ρi随着 i i i的增加而增大。当r是基本类的数量时,我们可能期望 ρ r ≈ 0 ρ_r≈0 ρr≈0,因为来自不同类的增广几乎组成了一个不相交的rway分区。然而,对于 i > r i > r i>r,我们可以期望 ρ i ρ_i ρi会大得多。例如,在极端情况下,当 i = ∣ X ∣ = N i = |X | = N i=∣X∣=N时,每个集合 S j S_j Sj都是一个单例,这意味着 ρ N = 1 ρ_N = 1 ρN=1。更一般地说,当 i i i大于数据中底层语义类的数量时,ρi可以期望在数据维数上至少是逆多项式。
Assumption 3.5 (at most
m
m
m clusters).
我们假设
ρ
m
+
1
≥
ρ
ρ_{m+1}≥ρ
ρm+1≥ρ。一个典型的情况是,在增强图中最多有
m
m
m个簇,每个簇都不能被分成两个狄利克雷电导都小于
ρ
ρ
ρ的子集。
□
\square
□
当有m个类簇有足够的内部连接时,我们期望 ρ m + 1 ρ_{m+1} ρm+1比 ρ m ρ_m ρm大得多,因为任何 m + 1 m+1 m+1分区都需要将一个子图额外分解成两部分并产生很大的狄利克雷电导。换句话说,假设图由 m m m个类簇组成, ρ ρ ρ描述了每个类簇内部连接的程度。实际上,我们将通过增强强度和亚种群分布的Cheeger常数(命题3.9)的乘积来正式降低 ρ m + 1 ρ_{m+1} ρm+1。
上述假设也暗示了图谱的性质。 γ i γ_i γi是归一化邻接矩阵 A A A和 γ 1 = 1 γ1 = 1 γ1=1的第i个最大特征值。根据Cheeger不等式, γ 2 m ≤ 1 − Ω ( ρ 2 / log m ) γ_{2m}≤1−Ω(ρ^2/ \log m) γ2m≤1−Ω(ρ2/logm),这表明 γ 1 γ_1 γ1和 γ 2 m γ_{2m} γ2m之间存在差距,这在我们的分析中很有用。
Assumption 3.6(标签可从其增广中恢复)
给定
x
‾
∈
P
X
‾
\overline x ∈ \mathcal P_\mathcal {\overline X}
x∈PX和它的标签
y
(
x
‾
)
y(\overline x)
y(x)。增广样本
x
∼
A
(
⋅
∣
x
‾
)
x \sim \mathcal A(\cdot | \overline x)
x∼A(⋅∣x)。我们假设存在一个分类器
g
g
g,它可以预测给定的
g
(
x
)
=
y
(
x
‾
)
g(x)=y(\overline x)
g(x)=y(x)的误差最多为
α
α
α。即正确概率至少为
1
−
α
1−α
1−α。
□
\square
□
假设3.6中的一个小的 α α α意味着不同的类是分离的的,因为来自不同类的数据只有很少个(最多O(α))共享数据增强。或者,我们可以将这个假设视为假设增强图可以划分为 r r r个簇,每个簇对应于一个类的增强,并且在簇中最多有O(α)边。这通常是正确的真实世界图像数据像ImageNet,因为任何两个图像从不同的类(例如,哈士奇和伯曼猫),使用典型的数据增广只能以指数的小概率 α α α得到相同的增强图像。
通常,Assumption 3.5 中的 ρ ρ ρ和Assumption 3.6中的 α α α都是远小于1的正值。然而, ρ ρ ρ可以比 α α α大得多。回想一下, ρ ρ ρ在维数上至少是反多项式。相比之下, α α α描述了类之间的分离,在典型情况下预计呈指数级小。例如,在使用高斯扰动增广的简单例子中,如果 σ d σ\sqrt d σd小于两个亚种群之间的最小距离,我们很少可以将来自不同亚种群的两个数据点增强为共享增强,因此α预计呈指数小。我们下面的分析是在ρ2大于α的合理状态下运行的,这直观地意味着集群内的内部连接大于集群之间的分离。我们还引入了以下假设,即假设类可以实现族群谱对比损失的最小化。
Assumption 3.7(假设类的表达性)。令 F \mathcal F F是一个包含从 X \mathcal X X到 R k \mathbb R^k Rk所有函数的假设类。我们假设 L ( f ) \mathcal L (f) L(f)的全局最小值中至少有一个属于 F \mathcal F F。
我们的主要定理依据上述最小化谱对比损失学习到特征的线性分类误差。在之后的定理中,我们将这个结果扩展到特征和线性头部都是从经验数据集中学习的情况。
Theorem 3.8(主要定理)。假设表征维数
k
≥
2
r
k≥2r
k≥2r且Assumption 3.6适用于
α
>
0
α > 0
α>0。设
F
\mathcal F
F是一个满足Assumption 3.7的假设类,
f
p
o
p
∗
=
min
f
L
(
f
)
f^∗_{pop}=\min_f \mathcal L (f)
fpop∗=minfL(f)。有:
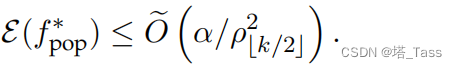
对于Assumption 3.5中
k
>
2
m
k>2m
k>2m,有
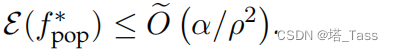 □
\square
□
□
\square
□
这里我们使用 O ( ⋅ ) \mathcal O(\cdot) O(⋅)来隐藏 k k k中的通用常数因子和对数因子。我们注意到,当来自不同类的增强在增强图中完全断开时, α = 0 α = 0 α=0,在这种情况下,上述定理保证了ground-truth的精确恢复。我们期望 α α α是一个非常(指数)小的、独立于 k k k的常数,而 ρ k / 2 ρ_{ k/2} ρk/2随着 k k k增加,当k相当大时,至少可以是逆多项式,因此比 α \sqrt α α大得多。我们将在下一小节中描述更具体分布上 ρ k ρ_k ρk的增长。当 k > 2 m k>2m k>2m时, α < < ρ 2 ≤ ρ m + 1 2 α <<ρ^2≤ρ^2_{m+1} α<<ρ2≤ρm+12,因此误差 α / ρ 2 α/ρ^2 α/ρ2足够小。
4. 待写
5. 待写
6. Experiment
6.1 Pseudo-code

注:常数项不需要优化,对于当前点
x
x
x,随机在mini batch中找到来自同意原始数据另一个增广点的期望为
1
/
N
1/N
1/N,在2N个增广样本中随机增广到当前点
x
x
x的期望
1
N
(
N
−
1
)
\frac{1}{N(N-1)}
N(N−1)1
6.2 Architecture
Encoder. 编码器f包含三个组成部分:
- Backbone是标准的ResNet-18 (CIFAR10/100)和ResNet-50(TinyImageNet & ImageNet)。
- Projection head是隐藏层和输出维度都为1000的2层MLP(CIFAR10/100)和隐藏和输出维度为8192的3层MLP(TinyImageNet & ImageNet),每一层都应用BatchNorm,除最后一层外,每一层都用ReLU激活。
- 投影函数取一个向量并将其投影到一个半径为
µ
\sqrt µ
µ的球面上,其中µ>0是我们在实验中调整的超参数。我们发现投影函数可以提高性能。一般设置
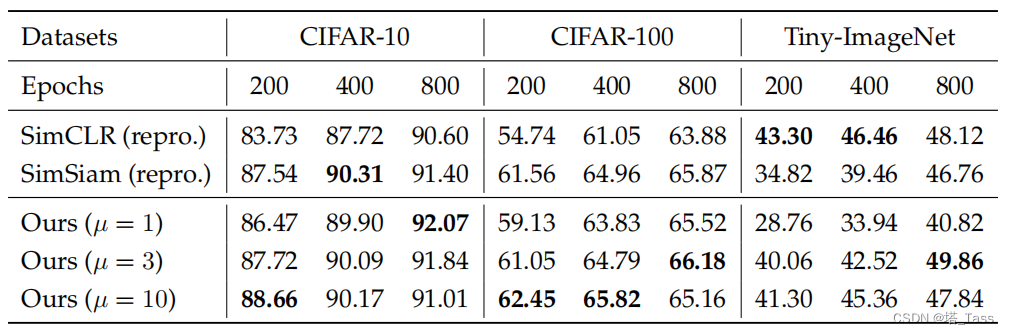
µ
∈
1
,
3
,
10
µ∈{1,3,10}
µ∈1,3,10,如以下消融实验所示:
Linear evaluation. 用得到的表征训练一个有监督的线性分类器,这些冻结的特征来自ResNet的全局平均池化层。
6.3 Results
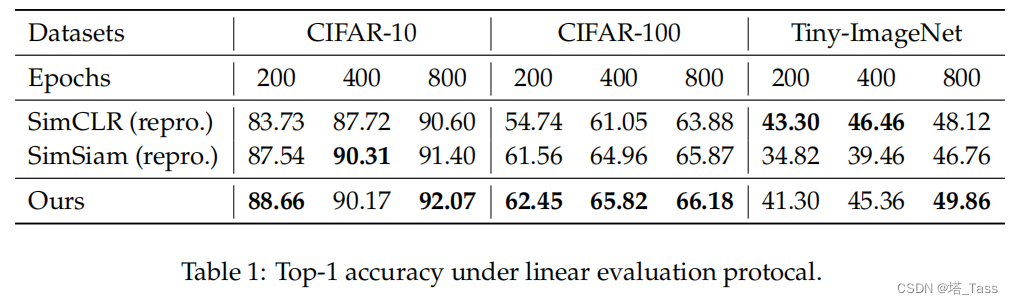
我们在表1中报告了CIFAR-10/100和TinyImageNet的准确性。我们的算法比以前的方法更有原则,不依赖大批量或额外的技巧如stop-gradient。





















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








