线性反馈移位寄存器（LFSR）和 Berlekamp-Massey 算法

应用密码学课上学习了 BM 算法，林老师说期末必考。做课后题时，让求解一个20长序列的 LFSR，本人算了两大页纸，还算错了两遍 (╬￣皿￣)

这里仔细研究下，谈谈我自己对它的理解。

LFSR

线性反馈移位寄存器（Linear-feedback shift register）可用于产生随机序列。有限域 $\mathbb{F}$ 上的 $n$ 级（包含$n$长的状态） LFSR 的结构如下：

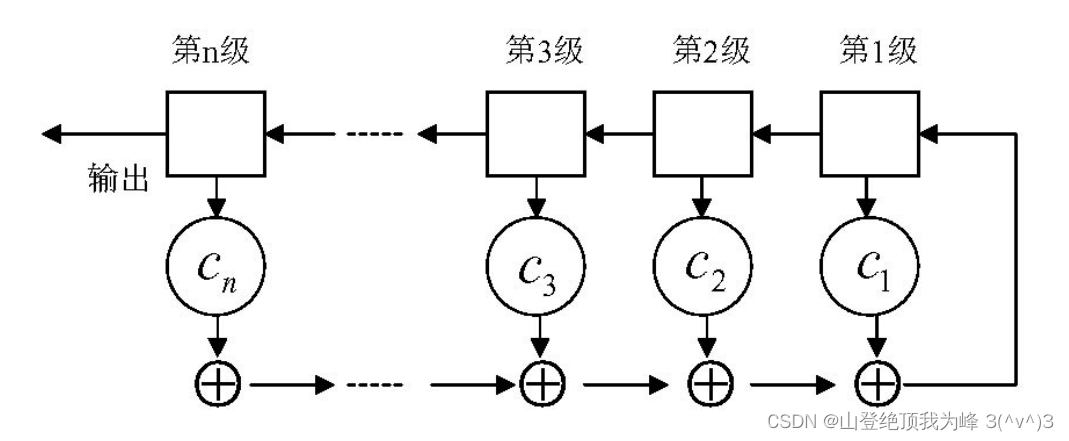
其中 $c_i\in \mathbb{F}$。如果$c_n=0$，那么是退化的 LFSR。反馈逻辑为线性递推关系：
$$a_k=\sum _{i+1}^n{c}_i{a}_{k-i}$$

特征多项式为：
$$f(x)=x^n+\sum _{i=1}^n{c}_i{x}^{n-i}$$

联接多项式为：
$$\tilde{f}(x)=1+\sum _{i=1}^n{c}_i{x}^i$$

易知，$\mathrm{deg}f=n$，$\mathrm{deg}\tilde{f}\le n$

用 $G(f)$ 表示由特征多项式 $f$ 可以生成的所有序列的集合，可以视为 $\mathbb{F}$上的$n$ 维向量空间。若 $\text{a}$ 是 $F_2$ 上的周期序列，那么当仅当存在一个多项式 $f$（极小多项式），使得 $\text{a}\in G(h)$ $⟺$ $h\in (f)$，这里 $(f)\subseteq F_2[x]$ 是个主理想。即，$f$ 是可以生成 $\text{a}$ 的次数最低的特征多项式，对应的 LFSR 的级数 $\mathrm{deg}f$ 叫做序列 $\text{a}$ 的线性复杂度。同时，周期 $p(\text{a})=p(f)$，这里 $p(f)$ 是满足 $x^e\equiv 1\mathrm{mod}f$ 的最小整数（多项式的阶，order）。

Berlekamp-Massey 算法

如果给定一个长度为 $N$ 的序列片段 $\text{a}=a_1{a}_2\cdots a_N\in {\mathbb{F}}^N$，已知它是由线性递归关系生成的。如何计算出生成它的最短的 LFSR ？

我们使用联接多项式 $f$ 以及阶数 $l$ 来描述 LFSR。我们将 $(f_N,l_N)$ 称作 $\text{a}$ 的线性综合解，如果 $f_N$ 对应的 $l_N$ 级 LFSR 是可以生成 $\text{a}$ 的阶数最小的 LFSR。

多项式乘积

给定序列 $\text{a}=a_1{a}_2\cdots a_n$，我们定义下述多项式
$$A(x)=1+a_{1}x+a_2{x}^2+\cdots a_n{x}^n\in {\mathbb{F}}^N$$

假设一个 $l_n$级的 LFSR 可以生成这个序列，对应的联接多项式为
$$f(x)=c_{l_n}{x}^{l_n}+\cdots +c_{1}x+1\in \mathbb{F}[x]$$

那么对于 $l_n+1\le k\le n$，要满足约束：
$$a_k+\sum _{i=1}^{l_n}{c}_i{a}_{k-i}=0\in \mathbb{F}$$

注意到 $a_k+{\sum }_{i=1}^{l_n}{c}_i{a}_{k-i}$ 就是 $f\cdot A$ 的单项 $x^k$ 的系数，也就是说：
$$f(x)\cdot A(x)=tai{l}_n(x)\mathrm{mod}{x}^{n+1}$$

这里 $tai{l}_n(x)$ 是多项式截尾，明显满足 $\mathrm{deg}(tai{l}_n)\le l_n$，这对应到 $f(x)$ 无法约束的可生成 $\text{a}[1:n]$ 所需的初始状态 $\text{a}[1:l_n]$（是自由的，无法被 LFSR 约束）

所以，我们想要找出最短的 LFSR，只需找出满足上述约束的联接多项式 $f(x)$。给定序列 $\text{a}$，BM 算法的思路是：迭代地构造一系列 $f_n$，使得 $(f_n,l_n)$ 是可以生成 $\text{a}[1:n]$ 的线性综合解，当 $n=N$ 时结束迭代。

思路

假设我们获得了 $(f_n,l_n)$，满足
$$f_n(x)\cdot A(x)=tai{l}_n(x)\mathrm{mod}{x}^{n+1}$$

也就是 $f_n$ 可以约束 $\text{a}[1:n]$

如果
$$f_n(x)\cdot A(x)=tai{l}_n(x)\mathrm{mod}{x}^{n+2}$$

那么 $f_n$ 依然可以约束 $\text{a}[1:n+1]$，从而 $(f_{n+1},l_{n+1}):=(f_n,l_n)$

如果
$$f_n(x)\cdot A(x)=tai{l}_n(x)+d_{n+1}{x}^{n+1}\mathrm{mod}{x}^{n+2}$$

其中 $d_{n+1}\ne 0\in \mathbb{F}$，那么说明 $f_n$ 无法约束 $\text{a}[1:n+1]$ 了，我们需要对它做调整。

我们寻找一个 $(f_m,l_m)$，它无法约束 $\text{a}[1:m+1]$，即
$$f_m(x)\cdot A(x)=tai{l}_m(x)+d_{m+1}{x}^{m+1}\mathrm{mod}{x}^{m+2}$$

那么，我们令
$$f_{n+1}(x)=f_n(x)-d_{n+1}{d}_{m+1}^{-1}{x}^{m-n}{f}_m(x)$$

画的草图：

可以验证：
$$\begin{array}{rl}{f}_{n+1}(x)\cdot A(x)& =f_n(x)\cdot A(x)-d_{n+1}{d}_{m+1}^{-1}{x}^{n-m}{f}_m(x)\cdot A(x)\\ & =tai{l}_n(x)+d_{n+1}{x}^{n+1}-d_{n+1}{d}_{m+1}^{-1}{d}_{m+1}{x}^{m+1}{x}^{n-m}-d_{n+1}{d}_{m+1}^{-1}{x}^{n-m}tai{l}_m(x)\\ & =tai{l}_n(x)-d_{n+1}{d}_{m+1}^{-1}{x}^{n-m}tai{l}_m(x)\mathrm{mod}{x}^{n+2}\end{array}$$

对应的 $tai{l}_{n+1}=tai{l}_n(x)-d_{n+1}{d}_{m+1}^{-1}{x}^{n-m}tai{l}_m(x)$，其度数为 $\mathrm{deg}(tai{l}_{n+1})\le \max (l_n,n-m+l_m)$

多项式选取

给定序列 $\text{a}=a_1{a}_2\cdots a_N\in {\mathbb{F}}^N$，我们首先找到第一个非零元素 $a_{n_0}\ne 0$

• 设置 $f_0=1$，对应的 $l_0=0$ 级的 LFSR 可以生成空序列。

• 对于 $1\le i<n_0$，明显 $\text{a}[1:i]=0^i$ 是零序列，从而可以由 $f_i(x)=1$ 的 $l_i=0$ 级的 LFSR 来生成。

• 对于 $i=n_0\ge 1$，序列 $\text{a}[1:n_0]=0^{n_0-1}\Vert 1$ 可以由任意的 $l_{n_0}=n_0$ 级的 LFSR 生成，方便起见选取：
  $$f_{n_0}=1-a_{n_0}{x}^{n_0}$$

容易看出，这些 $(f_i,l_i)$ 都是最短的 LFSR。易知，$l_{n_0}=\max (l_{n_0-1},n_0-l_{n_0-1})$，因为 $l_{n_0-1}=0$

后续将证明，每一次对 LFSR 的修正，从 $(f_m,l_m)$ 到 $(f_{m+1},l_{m+1})$，都会满足
$$l_{m+1}=\max (l_m,m+1-l_m)$$

这样，我们就获得了最初的 $(f_{n_0},l_{n_0})$，这个 LFSR 满足
$$f_{n_0}(x)\cdot A(x)=tai{l}_{n_0}(x)=0\mathrm{mod}{x}^{n_0+1}$$

也就是 $f_{n_0}$ 可以约束 $\text{a}[1:n_0]$，然后我们就可以迭代计算后续所有的 $(f_n,l_n)$ 了。

当我们遇到 $d_{n+1}\ne 0$ 时，我们可以这么选取 $f_m$：

1. 找到 $l_m<l_{m+1}=\cdots =l_n$，此时必然有 $f_m$ 无法约束 $\text{a}[1:m+1]$，于是存在对应的 $d_{m+1}\ne 0$ 是可逆元

2. 由于 $l_n=l_{m+1}=\max (l_m,m+1-l_m)>l_m$，因此必然有 $l_n=m+1-l_m$，从而 $n-m+l_m=n+1-l_n$，即
   $$\mathrm{deg}(tai{l}_n(x)-d_{n+1}{d}_{m+1}^{-1}{x}^{n-m}tai{l}_m(x))\le \max (l_n,n+1-l_n)$$

   因此，我们设置 LFSR 的级数为 $l_{n+1}=\max (l_n,n+1-l_n)$

定理 1：如果 $(f,l)$ 可以约束前 $n$ 项，而无法约束第 $n+1$ 项。那么对于可以生成前 $n+1$ 项的 LFSR，它的级数必然满足：
$$l^{\prime }\ge n+1-l$$

因此，上述的 $f_m$ 的选择就是最优的。使用其他的选择，得到的 LFSR $(f_{n+1},l_{n+1})$ 的级数不会更短。于是 BM 算法产生的每个 $(f_n,l_n)$ 就是可以生成 $a_1{a}_2\cdots a_n$ 的（不一定唯一）最短 LFSR。

定理 2：如果 $(f,l)$ 可以约束 $N$ 长的序列 $\mathbf{a}$ 的线性综合解，那么它是唯一解 $⟺2l\le N$

也就是说，如果求解的最终结果满足 $l_n\le n/2$，那么它就是唯一解，与一开始的 $f_{n_0}$ 的选择无关。但如果不是，那么选择其他的 $f_{n_0}$ 结果就可能会不一样（为了考试！），当然它们都是正确的 LFSR。

BM 算法

给定序列 $\text{a}=a_1{a}_2\cdots a_N\in {\mathbb{F}}^N$，算法如下：

1. 初始化步骤

   1. 设置 $d_0=0$，$f_0=1$，$l_0=0$
   2. 如果 $a_i=0,\forall 1\le i<n_0$，那么设置 $d_i=0$，$f_i=1$，$l_i=0$
   3. 设置 $d_{n_0}=a_{n_0}$，$f_{n_0}=1-d_{n_0}{x}^{n_0}$，$l_{n_0}=n_0$

2. 迭代步骤

   1. 假设已经获得了 $(f_n,l_n)$，那么计算 $d_{n+1}=a_{n+1}+{\sum }_{i=1}^{l_n}{c}_i{a}_{n+1-i}$
   2. 如果 $d_{n+1}=0$，那么设置 $f_{n+1}=f_n$，$l_{n+1}=l_n$
   3. 如果 $d_{n+1}\ne 0$，那么
      1. 寻找 $l_m<l_{m+1}=\cdots =l_n$ 的 $m$ 对应的 $f_m$ 和 $d_{m+1}\ne 0$
      2. 设置 $f_{n+1}=f_n-d_{n+1}{d}_{m+1}^{-1}{x}^{n-m}{f}_m$，$l_{n+1}=\max (l_n,n+1-l_n)$
   4. 当 $n+1=N$ 时，结束迭代，输出 $(f_N,l_N)$

例子