人工智能-作业3：使用backward()例题程序复现

最新推荐文章于 2025-12-02 15:55:42 发布

原创

最新推荐文章于 2025-12-02 15:55:42 发布 · 873 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #pytorch #深度学习

本文通过对比手动反向传播和PyTorch的backward()函数，探讨两者在神经网络训练中的差异。作者展示了如何使用backward()进行梯度计算，并讨论了ReLU激活函数、损失函数的选择及其对训练的影响。实验结果表明，虽然手动计算可能出错，但backward()能准确记录计算图，简化编程过程。

使用pytorch复现例题

将反向传播的过程用backward()实现，并且在每次计算梯度之后记得清除梯度。

import torch

def sigmoid(z):
    a = 1 / (1 + torch.exp(-z))
    return a

def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8):
    in_h1 = w1 * x1 + w3 * x2  # 隐藏层
    out_h1 = sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)

    in_o1 = w5 * out_h1 + w7 * out_h2  # out
    out_o1 = sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)

    print("正向计算：o1 ,o2")  # 输出本轮进入损失函数之前的数值out1、out2
    print(out_o1.data, out_o2.data)  # round()舍入化整，round(x,y),y表保留小数后几位，此处保留5位小数
    # 损失函数MSE 均方误差：1/n * sum((y^-y)**2)
    # 此处只有2个y，所以n=2
    error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2

    print("损失函数：均方误差")  # 输出本轮损失函数
    print(error.data)
    return error

if __name__ == "__main__":
    w1 = torch.Tensor([0.2])
    w2 = torch.Tensor([-0.4])
    w3 = torch.Tensor([0.5])
    w4 = torch.Tensor([0.6])
    w5 = torch.Tensor([0.1])
    w6 = torch.Tensor([-0.5])
    w7 = torch.Tensor([-0.3])
    w8 = torch.Tensor([0.8])
    x1 = torch.tensor(0.5)
    x2 = torch.tensor(0.3)
    y1, y2 = 0.23, -0.07
    w1.requires_grad = True
    w2.requires_grad = True
    w3.requires_grad = True
    w4.requires_grad = True
    w5.requires_grad = True
    w6.requires_grad = True
    w7.requires_grad = True
    w8.requires_grad = True

    for i in range(100):
        print("=====第" + str(i) + "轮=====")
        error = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
        error.backward()
        print("反向传播：误差传给每个权值")
        print(w1.grad.data, w2.grad.data, w3.grad.data, w4.grad.data, w5.grad.data, w6.grad.data,
              w7.grad.data, w8.grad.data)
        w1.grad.item()# w.grad.data:获取梯度，用data计算，不会建立计算图，每次获取叠加到grad
        w2.grad.item()
        w3.grad.item()
        w4.grad.item()
        w5.grad.item()
        w6.grad.item()
        w7.grad.item()
        w8.grad.item()
        # 修正一次w,步长为step
        step = 1
        w1.data = w1.data - step * w1.grad.data
        w2.data = w2.data - step * w2.grad.data
        w3.data = w3.data - step * w3.grad.data
        w4.data = w4.data - step * w4.grad.data
        w5.data = w5.data - step * w5.grad.data
        w6.data = w6.data - step * w6.grad.data
        w7.data = w7.data - step * w7.grad.data
        w8.data = w8.data - step * w8.grad.data
        print("更新后的权值")
        print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
        w1.grad.data.zero_()     # 注意:将w中记录的梯度清零，消除本次计算记录，只保留新的w，开启下一次前向传播
        w2.grad.data.zero_()
        w3.grad.data.zero_()
        w4.grad.data.zero_()
        w5.grad.data.zero_()
        w6.grad.data.zero_()
        w7.grad.data.zero_()
        w8.grad.data.zero_()

两个方法对比

我设计的是100轮（0~99），此时得到的结果是：

=第99轮=
正向计算：o1 ,o2
tensor([0.2378]) tensor([0.0736])
损失函数：均方误差
tensor([0.0103])
反向传播：误差传给每个权值
tensor([-0.0031]) tensor([-0.0015]) tensor([-0.0019]) tensor([-0.0009]) tensor([0.0010]) tensor([0.0067]) tensor([0.0007]) tensor([0.0052])
更新后的权值
tensor([0.9865]) tensor([-0.2037]) tensor([0.9719]) tensor([0.7178]) tensor([-0.8628]) tensor([-2.8459]) tensor([-1.0866]) tensor([-1.1112])

用上次手推法计算的结果得到的却是：

=第99轮=
正向计算：o1 ,o2
0.26472 0.11372
损失函数：均方误差
0.01748
反向传播：误差传给每个权值
0.00154 0.00133 0.00092 0.0008 0.00329 0.00901 0.0029 0.00794
更新后的权值
-0.25 -0.79 0.23 0.36 -0.99 -3.0 -1.26 -1.4

差的不是一般的多……这两种方法唯一的区别就在反向传播处，也就是说手推法的反向传播有地方算错了。
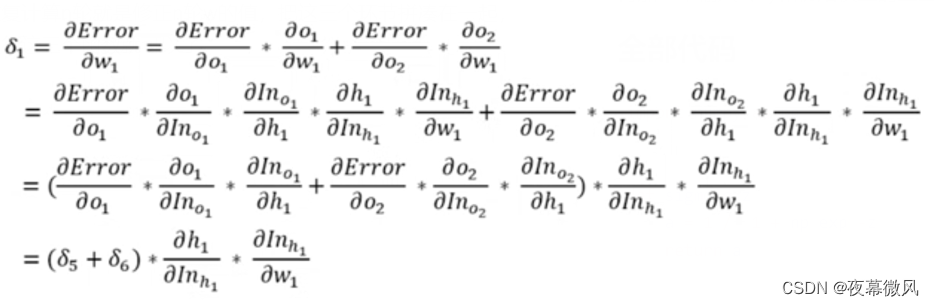
在这里插入图片描述
当时看这个的时候发现它没写h1是out还是in，感觉和我之前推的过程不一样，就没仔细算，直接拿来用了，结果果然出问题了（汗），事实证明人还是不能偷懒……
实际上应该是算成这样的：
$\frac{\partial error}{\partial w_1}= \frac{\partial error}{\partial out\_o_1}\cdot \frac{\partial out\_o_1}{\partial w_1}+ \frac{\partial error}{\partial out\_o_2}\cdot \frac{\partial out\_o_2}{\partial w_1}$
$\frac{\partial error}{\partial out\_o_1}\cdot \frac{\partial out\_o_1}{\partial in\_o_1}\cdot \frac{\partial in\_o_1}{\partial out\_h_1}\cdot \frac{\partial out\_h_1}{\p$