单片空间后方交会 python实现

空间后方交会 python实现

在学校上摄影测量课时，老师给了c的代码来实现后方交会
自己也闲暇时间在学习python，所以自己编程实现空间后方交会求解六个外方位元素（三个线元素，三个角元素）
就用书上的例题得数据，存成了csv格式：

没有设置精度标准，但是可以自己定义迭代次数，需要精度评定的话可以加在循环里。
例题里是四个像点和地面控制点，但写程序得时候没有针对四个点编，如果有更多的点位也是可以的。才疏学浅，应有很多效率更高的法，日后学习了，再多多改进。

题中应用的空间后方交会公式：

共线方程结算外方位元素公式：

进行线性化后：

系数阵元素：

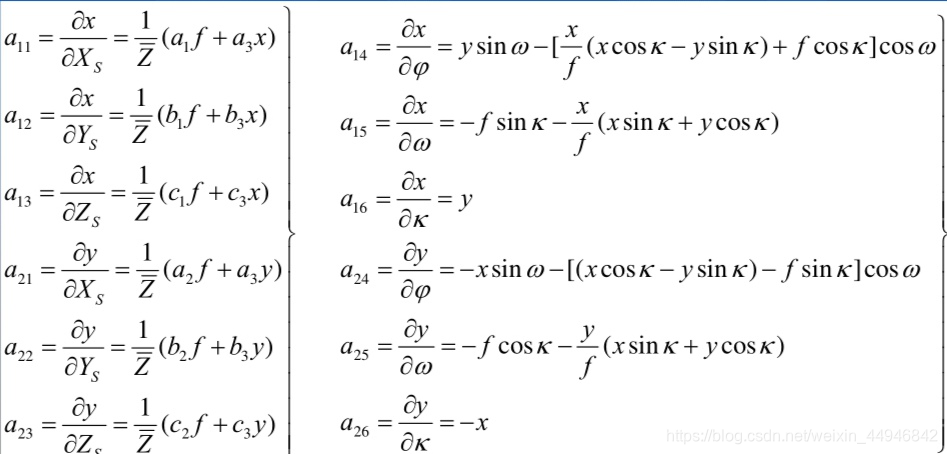
像片倾角小于3°，所以外方位角元素近似取为0，近似后如下：


通过公式进行平差计算：

代码如下：

import numpy as np
from math import*
print('请将数据命名为坐标数据并保存为CSV格式\n')
original_data=np.loadtxt(open('坐标数据.csv'),delimiter=",",skiprows=0)
#读取数据为矩阵形式
print('原始数据如下(x,y,X,Y,Z):\n',original_data)
m=eval(input("请输入比例尺（m）："))
f=eval(input("请输入主距（m）："))
x0,y0=eval(input("请输入x0，y0（以逗号分隔）："))
num=eval(input('请输入迭代次数：'))
xy=[]
XYZ=[]
fi,w,k=0,0,0  #一般相片倾角小于3°所以外方位元素近似取φ，ω，κ=0
#读取影像坐标，存到xy列表，相应地面点坐标存到XYZ列表
for i in range(len(original_data)):
    xy.append([original_data[i][0]/1000,original_data[i][1]/1000])
    XYZ.append([original_data[i][2],original_data[i][3],original_data[i][4]])
#定义系数矩阵A，常数项矩阵L
A = np.mat(np.zeros((len(xy*2),6)))
L = np.mat(np.zeros((len(xy*2),1)))
#将xy和XYZ列表转化为矩阵
xy=np.mat(xy)
XYZ=np.mat(XYZ)
XYZ_CHA=np.mat(np.zeros((len(xy),3)))    #便于推到偏导数建立的矩阵
sum_X=0
sum_Y=0
#Xs0 Ys0 取四个角上控制点坐标的平均值   Zs0=H=mf
for i in range(len(original_data)):    
    sum_X=original_data[i][2]+sum_X
    sum_Y=original_data[i][3]+sum_Y
Xs0=0.25*sum_X
Ys0=0.25*sum_Y
Zs0=m*f
diedai=0
while(diedai<num):
    #旋转矩阵
    a1=cos(fi)*cos(k)-sin(fi)*sin(w)*sin(k)
    a2=(-1.0) * cos(fi) * sin(k) - sin(fi) * sin(w) * cos(k)
    a3=(-1.0) * sin(fi) * cos(w)
    b1=cos(w) * sin(k)
    b2=cos(w) * cos(k)
    b3=(-1.0) * sin(w)
    c1=sin(fi) * cos(k) + cos(fi) * sin(w) * sin(k)
    c2=(-1.0) * sin(fi) * sin(k) + cos(fi) * sin(w) * cos(k)
    c3=cos(fi) * cos(w)
    xuanzhuan=np.mat([[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]])
    for i in range(len(XYZ)):
        XYZ_CHA[i,0]=XYZ[i,0]-Xs0
        XYZ_CHA[i,1]=XYZ[i,1]-Ys0
        XYZ_CHA[i,2]=XYZ[i,2]-Zs0
    XYZ_=xuanzhuan.T*XYZ_CHA.T
    for i in range(len(XYZ)):
#系数阵：
        A[i*2,0]=-f/(Zs0-XYZ[i,2])
        A[i*2,1]=0
        A[i*2,2]=-xy[i,0]/(Zs0-XYZ[i,2])
        A[i*2,3]=-f*(1+pow(xy[i,0],2)/pow(f,2))
        A[i*2,4]=-(xy[i,0]*xy[i,1])/f
        A[i*2,5]=xy[i,1]
        A[i*2+1,0]=0
        A[i*2+1,1]=-f/(Zs0-XYZ[i,2])
        A[i*2+1,2]=-xy[i,1]/(Zs0-XYZ[i,2])
        A[i*2+1,3]=-(xy[i,0]*xy[i,1])/f
        A[i*2+1,4]=-f*(1+pow(xy[i,1],2)/pow(f,2))
        A[i*2+1,5]=-xy[i,0]
#常数项：
        L[i * 2,0]=xy[i,0]+f*(XYZ_[0,i]/XYZ_[2,i])
        L[i * 2 + 1,0] =xy[i,1]+f*(XYZ_[1,i]/XYZ_[2,i])
#结果：
    Result=((A.T*A).I)*A.T*L
    Xs0+=Result[0]
    Ys0+=Result[1]
    Zs0+=Result[2]
    fi+=Result[3]
    w+=Result[4]
    k+=Result[5]
    diedai=diedai+1
a1=cos(fi)*cos(k)-sin(fi)*sin(w)*sin(k)
a2=(-1.0) * cos(fi) * sin(k) - sin(fi) * sin(w) * cos(k)
a3=(-1.0) * sin(fi) * cos(w)
b1=cos(w) * sin(k)
b2=cos(w) * cos(k)
b3=(-1.0) * sin(w)
c1=sin(fi) * cos(k) + cos(fi) * sin(w) * sin(k)
c2=(-1.0) * sin(fi) * sin(k) + cos(fi) * sin(w) * cos(k)
c3=cos(fi) * cos(w)
rotate=np.mat([[a1,a2,a3],[b1,b2,b3],[c1,c2,c3]])
print('计算结果\n',Xs0,'\n',Ys0,'\n',Zs0,'\n')
print('旋转矩阵\n',rotate)
print('迭代次数为：',diedai)
input()

运行结果：
刚学习python，边学边编，兴许有漏洞，算法还有改进空间，也参考了老师给的c代码得一些思路。仍有不足，还望读者多多包含。

参考文献：
[1]杨可明. 摄影测量学基础[M]. 北京：中国电力出版社,2011：38-50