- 学习网址:http://edu.mathor.com/course/292
- 资料下载:https://wws.lanzous.com/b01hntbsf 密码:850t
目 录
1.问题初步解析
分析题目:找关键词
找方法预测未来数据、控制疫情
预测模型:时间序列分析、线性拟合、非线性拟合、插值拟合、回归、人工神经网络、微分方程、偏微分方程(描述连续变化情况)、灰色预测
控制:动态调参过程、改变外在条件(参数)、控制疫情-->目标:感染人数越少越好 减少条件->优化 运筹学 规划:线性规划、非线性规划、整数规划
构建目标函数、约束条件 灵敏度分析:调参 观察改变参数后,结果是怎样的。
关键词:传染病------->国赛:非典问题
问题1分析
国家:庞大、包括很多城市、全局范围;城市:小区域、局部范围。
传染病模型:元胞自动机、微分方程模型(相对准确、完善的模型)、扩散机理、传播途径、致病机理
灰色预测:无法得知内在关联、无法从本质原理上解释
模型受到很多干扰情况、黑人...
微分方程模型:随时间、空间 有规律地变化 --》 算出变化率、构建微分方程组、解出函数表达式
问题2分析
SI、SIS、SIR
灵敏度分析:通过调参(改变参数数值),增加或减少10%、20%、30%...,观察结果的变化(可能是不同人群的数量的变化趋势)。
误差分析:与实际数据进行对比。不同参数情况下,与实际数据进行对比,看哪个参数对应的数据与实际数据最为吻合。得出相对误差
稳定性分析:结果(模型)是否稳定、看参数对模型结果的影响大不大、【大:不稳定;小:稳定】
问题2关键词:灵敏度分析
问题3分析
等待排队时间(买票、打饭):一般是泊松分布 负指数分布:
概率论数理统计问题
排队论求解
问题4分析
美赛:连环犯罪罪犯的寻找 给出凶杀案地理位置,找出罪犯的可能藏身地点 规律??? 溯源???
模型:圆的半径知识求解(以圆为半径,四周扩展)... 图论知识(案件地点:节点;找度最大的节点)
美赛:电话信息、短信-->搜索犯罪头目
问题5分析
可行性:灵敏度分析、溯源、隔离强度的调控、数学模型的分析->得出有效结论、评判建议的实施难易程度(增强隔离强度)、对每一条措施进行分析(可能性有多大)、
国赛:太阳影子定位
问题核心总结
问题核心总结:
- 微分方程
- 灵敏度分析
- 排队论与概率统计
- 溯源(土语网络模型、圆的知识、其他文献溯源方法)
- 建议与措施、可行性分析
2.模型假设
仅作参考
1.方便微分方程组的建立,di / dt
3.问题分析
数值解、解析解
4.模型的建立和求解
机理不同、模型假设不同
SEIR模型:考虑了隔离强度,相对简单。
5.传染病模型的建立
△t 很小很小:差分方程--转-->微分方程组
1、控制前阶段
2、控制后阶段
考虑隔离强度p
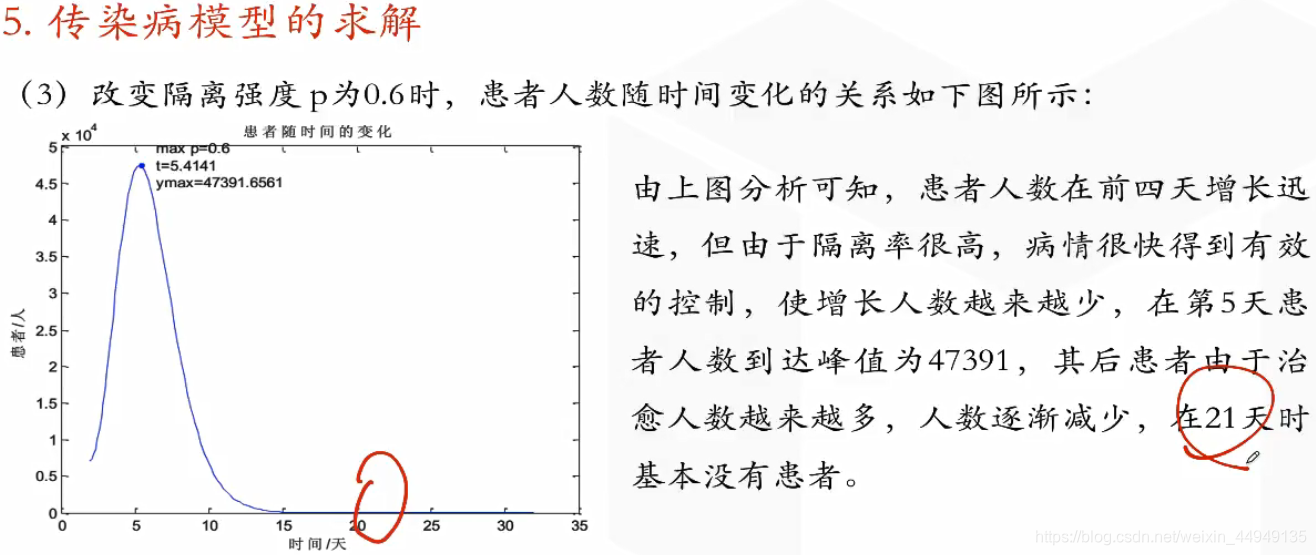
5.传染病模型的求解
1、控制前
2、控制后
3、控制前后模型总体
居家隔离
6.模型评价
优点
缺点
患者死亡概率
7.模型应用
问题5的建议
病毒特点:人传人、溯源之地、海鲜、病毒变异、野生动物、实验室原因
及时公开数据,避免造成人心惶惶... 科学引导
8.参考文献
9.附录
1.问题分析
2.模型假设
3.排队论模型的建立
4.排队论模型的求解
>1:超载
5.模型改进
6.附录
2. 模型一 圆周假设理论改进模型
3. 模型二 中心图解法
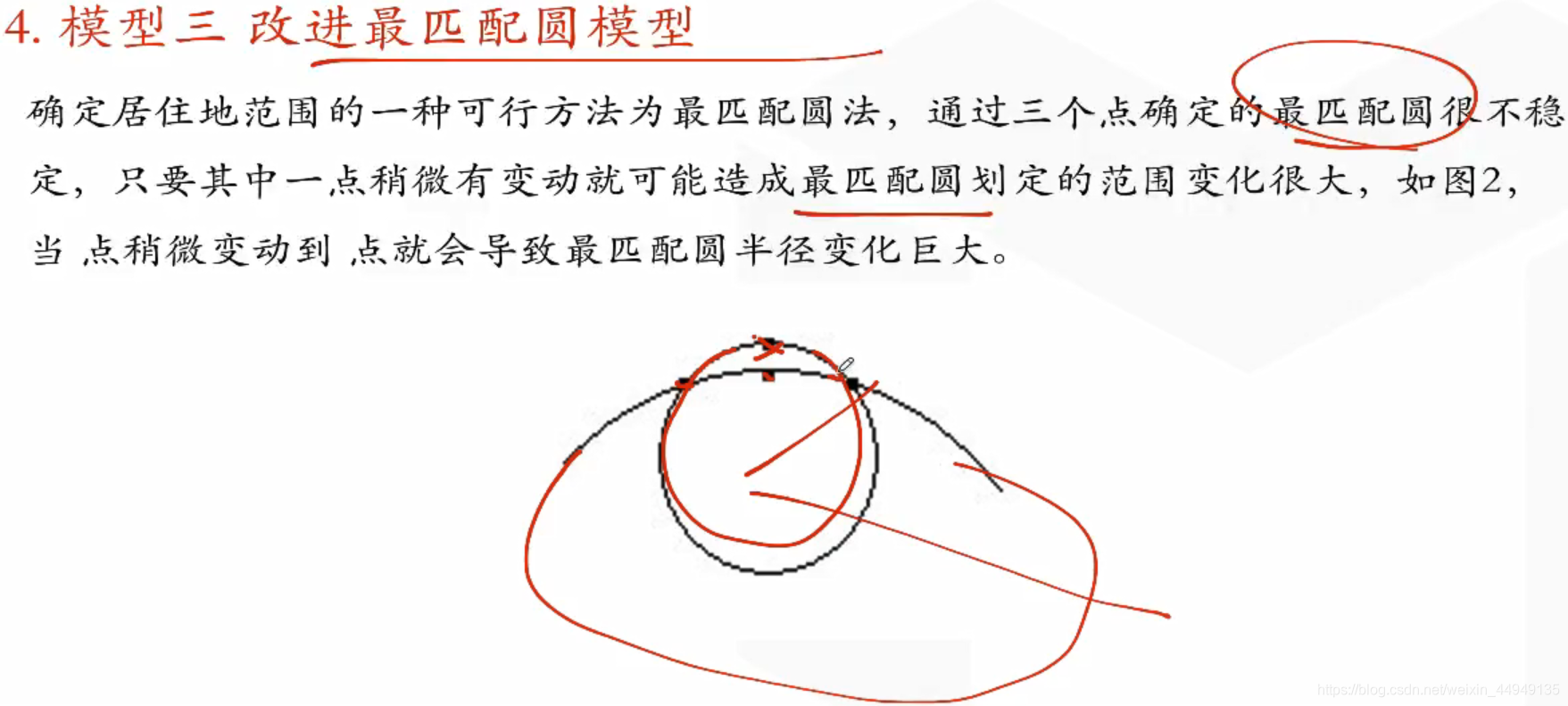
4. 模型三 改进最匹配圆模型
5. 模型四 Rossmo公式预测模型
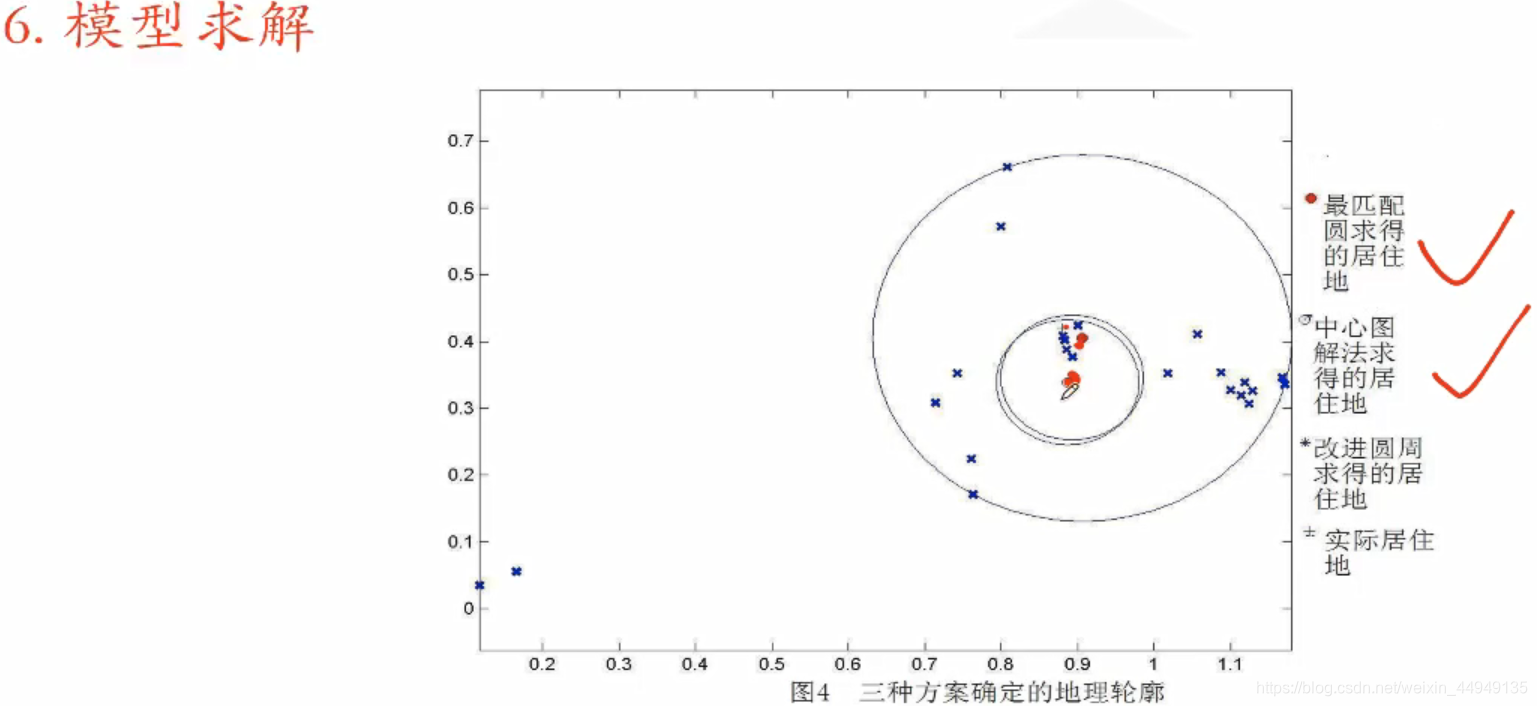
6.模型求解
7.参考文献
总结:微分方程、灵敏度分析、参数分析、优化、溯源、排队论、概率统计、写信、实际数据---非线性拟合







































































































 3023
3023

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










