Radar Toolbox第一讲——雷达增益与损失

最新推荐文章于 2024-08-19 10:02:21 发布

小学导航员

最新推荐文章于 2024-08-19 10:02:21 发布

阅读量1.9k

点赞数 3

文章标签：信号处理

原文链接：https://ww2.mathworks.cn/help/radar/ug/surveillance-radar-gains-and-losses.html

版权

Radar Toolbox第一讲——雷达增益与损失

为使用matlab对雷达性能进行仿真，自己造轮子，从信号产生开始，太麻烦了，偷懒的话可以直接从雷达工具箱开始。

雷达工具箱包括用于设计、模拟、分析和测试多功能雷达系统的算法和工具，可以进行链路分析和权衡，构建发射机、接收机、信道、目标、干扰等模型，并进行目标检测。

官网Radar Toolbox Documentation - MathWorks 中国

可用信噪比

雷达方程包含雷达系统的主要参数，决定了雷达系统的最大探测范围所需的峰值发射功率或最大可用信噪比。使用基本雷达方程，计算一定范围内的最大可用信噪比SNR是：

Pt是峰值发射功率

τ是发射的脉冲宽度

Gt是发射天线增益

Gr是接收天线增益

λ是雷达波长

σ是雷达目标散射截面（RCS）

k是玻尔兹曼常数

Ts是系统噪声温度

L是沿发射机-目标机-接收机路径组合损耗的一般损耗因子，可降低接收信号能量。

除目标RCS之外得参数都可以由设计人员决定，可以通过传输更多功率、增加天线尺寸、使用更低的频率或具有更灵敏的接收器来增加接收器上可用的信噪比

仿真使用3 GHz 频率运行的 S 波段脉冲雷达。峰值发射功率为0.2 MW，发射和接收天线增益为34 dB，脉冲持续时间为11Ms，噪声系数为4.1 dB。假设需要雷达探测距离100km的，RCS是1 m² 的目标。

lambda = freq2wavelen(3e9);         % Wavelength (m)
Pt = 0.2e6;                         % Peak power (W)
tau = 1.1e-5;                       % Pulse width (s)
G = 34;                             % Transmit and receive antenna gain (dB)
Ts = systemp(4.1);                  % System temperature (K) 
rcs = 1;                            % Target radar cross section (m^2)
Rm = 100e3;                         % Required maximum range (m)

首先，假设没有损失，也就是说L= 0 dB。使用基本雷达方程来计算接收机处的可用信噪比作为目标距离的函数。

%按照40m采样点计算，损失为0，计算每个距离对应所需要的SNR
L = 0;                              % Combined transmission line and propagation losses (dB)
R = (1:40:130e3).';                 % Range samples (m)
SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'Loss',L);

计算100km对应处可用SNR

SNRatRm = SNR(find(R>=Rm,1))

SNRatRm = 18.3169

绘制出按照距离衰减的的可用信噪比变化

radarmetricplot(R*1e-3,SNR,'MetricName','Available SNR','MaxRangeRequirement',Rm*1e-3,...
    'RangeUnit','km','MetricUnit','dB','RadarName',{'Surveillance Radar'});
legend('Location','best');

所需 SNR

根据计算的可用信噪比，判断其是否足够高满足检测。

雷达接收器处理的信号是发射波形和随机噪声的组合，因此能否检测到取决于所需的检测概率Pd，最大可接受的误报概率Pfa.

这些概率定义了所需的 SNR，也称为可检测性因子（或可检测性）。可检测性因子是声明具有指定检测概率和误报概率的检测所需的最小 SNR。它还取决于 RCS和探测器的类型。

目标检测原理

雷达信号判断目标是否存在，通常使用的是门限检测，即就是接收的信号有发射的波形和噪声，因此在接收端会存在四种情况

存在目标，判断为有目标——正确判断，称为发现，发现概率Pd

存在目标，判断为无目标——错误判断，称为漏报，漏报概率Pla

不存在目标，判断为有目标——错误判断，称为虚警，虚警概率Pfa

不存在目标，判断无有目标——正确判断，称为正确不发现，正确不发现概率Pan

Pd+Pla=1

Pfa+Pan=1

通常使用虚警概率和漏报概率

雷达检测性能有其发现概率和虚警概率来描述，Pd越大，发现目标的可能性越大，于此同时会希望Pfa的值不饿能超过允许值，接收机端的信号比和检测性能直接相关，因此需要在确定的Pd和Pfa情况下确定需要的SNR

目标截面积

雷达是利用目标散射功率来发现目标的，所以RCS也影响雷达得检测性能，目标的RCS和检测性能直接相关，日常使用中将给定目标的RCS定位常值，但是实际中其因为运动是在变化的，所以对于RCS的描述需要确定其概率密度函数和相关函数。通常从使用施维林起伏模型进行描述。

施维林起伏模型有两种不同的概率密度函数，又可以分为相关和不相关；

慢起伏：天线扫描器件回波起伏完全相关，扫描间完全不相关

快起伏：回波起伏在脉冲与脉冲之间完全相关。

仿真

假设Pd= 0.9 和Pfa=1e-6，使用Swerling 0模型目标，接收单个脉冲的可检测性因子：

Pd = 0.9;
Pfa = 1e-6;
D0 = detectability(Pd,Pfa,1,'Swerling0')
D0 = 13.1217

使用 Swerling 1模型目标计算的可检测性因子（该模型更准确），其单脉冲可探测因子明显更高。

D1 = detectability(Pd,Pfa,1,'Swerling1')
D1 = 21.1436

使用该模型计算的所需SNR 21.4 大于可用SNR 18.3，意味着单个脉冲将无法检测到 Swerling 1 目标。降低可检测性因子的常用方法是进行脉冲积分。计算N= 10 个非相干积分脉冲。

N = 10;
DN = detectability(Pd,Pfa,N,'Swerling1')
DN = 13.5033

非相关积累后的所需SNR13.5小于可用SNR 18.3所以可以在给定概率下可以检测到目标

Swerling 1 模型目标计算的可检测性因子和N脉冲结合了积分增益和波动损耗的影响。计算单次和脉冲积累前后的积分增益

Gi = detectability(Pd,Pfa,1,'Swerling0') - detectability(Pd,Pfa,N,'Swerling0')
Gi = 7.7881

起伏损失是检测起伏目标所需的信噪比与检测稳定目标所需的信噪比之间的差值。

Lf = detectability(Pd,Pfa,N,'Swerling1') - detectability(Pd,Pfa,N,'Swerling0')
Lf = 8.1696

使用radarbudgetplot函数说明可检测性因子的组成部分。

如果helperDetectabilityWaterfallPlot报错

就将 Modeling Radar Detectability Factors添加到路径

helperDetectabilityWaterfallPlot([D0 -Gi Lf], {'Single-pulse steady target','Pulse integration gain','Fluctuation loss'});
title('Detectability Factor')

计算出可检测因子后，代入雷达方程的距离形式，作为评估系统实际最大距离所需的最小信噪比。

radareqrng(lambda,DN,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'Loss',L,'unitstr','km')
ans = 131.9308

为清楚地指出所需的检测概率Pd和最大可接受的虚警概率Pfa的范围，将可检测性因子作为水平线添加到 SNR 与范围图中。

红色区域内无法检测指定的pd和pfa，

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(No Losses)'}]);
legend('Location','best');

超出所需最大范围的所有范围都显示为绿色，并标记为“通过”。

该分析假设零损耗，因此无法充分预测实际雷达系统的范围。由于以下原因，具有指定参数的真实雷达系统将具有较短的最大范围：

地球表面和大气层引起的传播效应。这些效应会减少接收器的可用信号能量。
整个雷达系统经历了各种损失。此类别中的某些损失会降低可用的信噪比，而其他损失则会导致可检测性因子增加。

以下各节更详细地考虑了属于第二类的损耗对雷达系统测距性能的影响。

距离相关因素

在设计监视雷达系统时，雷达方程中必须包括几个因素，以解释接收机可用信号能量的减少。

信号遮挡

脉冲雷达系统在脉冲传输过程中关闭接收器。因此，从距离雷达一个脉冲长度以内或在无模糊范围附近的一个脉冲长度范围内到达的目标回波将被发射的脉冲所掩盖，导致只有一小部分脉冲被接收和处理。本例中考虑的雷达系统的脉冲宽度为11μs，则可以接收全脉冲的最接近范围是最小范围R_min.

Rmin = time2range(tau)
Rmin = 1.6489e+03

则距离小于 1649 m 的目标的回波将在脉冲传输完成之前到达，对于位于无模糊范围的倍数或附近的目标，可以观察到类似的效果。假设脉冲重复频率为 1350 Hz（脉冲重复间隔T≈0.75 ms），计算系统的无模糊距离。

prf = 1350;                         % Pulse repetition frequency
Rua = time2range(1/prf)
Rua = 1.1103e+05

从距离*R_ua*±R_min到达的回波将被下一个发送的脉冲所遮盖。下图说明了脉冲遮蔽，箭头指示脉冲的前面

由于信号遮蔽，可用的SNR将在0距离和等于Rua的倍数的距离内具有较深的零陷。为了考虑由于脉冲遮蔽而导致的可用SNR损失，必须将遮蔽因子添加到雷达方程中。

Du = tau*prf;                       % Duty cycle
Fecl = eclipsingfactor(R,Du,prf);   % Eclipsing factor

SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'CustomFactor',Fecl,'Loss', L);

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With Eclipsing)'}]);
legend('Location','best');

真实世界的雷达系统利用PRF分集来防止遮挡损失并扩大系统的无模糊范围。

灵敏度时间控制（STC）

典型的监视雷达系统必须传输相当大的功率才能远距离探测目标。尽管可用能量会随着距离的增加而迅速衰减，但在非常近的距离内，由于高峰值发射功率，即使是小目标也可以获得非常强劲的回报。来自小型干扰目标（鸟类、昆虫）的强回波可能会导致不良检测，而常规大小的目标或附近的杂波可能会使接收器饱和。监视雷达系统非常希望避免这种干扰检测。为了解决这个问题，雷达系统使用STC。它将接收器增益扩展到截止范围R_STC在目标接近雷达时保持恒定的信号强度。

获取

Rstc = 60e3;                        % STC cutoff range (m)
Xstc = 4;                           % STC exponent selected to maintain target detectability at ranges below Rstc (since the signal power is inversely proportional to R^4)
Fstc = stcfactor(R,Rstc,Xstc);      % STC factor

SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'CustomFactor',Fecl+Fstc,'Loss',L);

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC and Eclipsing for 1 m^2 Target)'}]);
legend('Location','best');
ylim([-30 30])

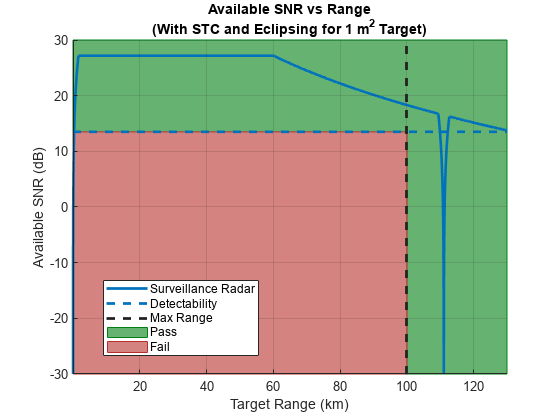
加上STC因子后，图中显示1 m2 的RCS目标仍然在最大范围内被检测到，但是RCS为0.03 m的小目标2将无法达到所需的Pd=0.9 在任何范围内，因此将被拒绝。

从图中可以清楚地看出，STC仅将可用的SNR扩展到指定的截止范围，而不会影响最大探测范围内的可用SNR。

扫描

雷达系统可以通过机械旋转天线或使用相控阵天线并执行电子扫描来扫描目标。天线波束的不完美形状以及波束在搜索体积上扫描的过程会给系统带来额外的损耗。

波束形状损失

雷达方程使用天线增益的峰值，假设每个接收的脉冲都具有最大振幅。实际上，当波束通过目标时，接收到的脉冲被扫描天线的双向模式调制，从而导致波束形状损失。计算这种损耗的确切值需要知道确切的天线方向图。在通常执行此类分析时，在雷达系统设计的早期阶段可能无法获得此信息。相反，典型实用天线的主瓣形状可以很好地近似于高斯形状。假设雷达系统在空间域内进行密集采样（波束移动小于半功率波束宽度的0.71），计算一维扫描的波束形状损失。

Lb = beamloss
Lb = 1.2338

如果雷达系统同时在方位角和仰角上进行扫描，波束形状损失会加倍。

beamloss(true)
ans = 2.4677

扫描扇区损失

假设雷达系统采用电子控制相控阵来执行扫描。使用相控阵天线将导致所需信噪比的增加，这是由于两个影响：

1）由于波束方向上的投影阵列面积减小而导致波束展宽，

2）在偏宽角下单个阵列元件的有效孔径面积减小。

考虑以上影响，将扫描扇区损失添加到可检测性因子中。假设示例中的系统仅在方位角维度上进行扫描，并且扫描扇区范围为 –60 到 60 度。计算由此产生的损失。

theta = [-60 60];
Larray = arrayscanloss(Pd,Pfa,N,theta,'Swerling1')
Larray = 2.7745

信号处理

在检测之前，接收到的雷达回波必须通过雷达信号处理链。信号处理链中不同组件的目的是保证所需的检测概率和误报，抑制杂波中不需要的回波，并考虑可变或非高斯噪声。我们进一步考虑了监视雷达系统中必须考虑的信号处理损耗的几个组成部分。

MTI

移动目标指示器（MTI）是一个拒绝固定或缓慢移动的杂波的过程，同时传递来自以显着速度移动的目标的回波。典型的 MTI 使用 2、3 或 4 脉冲消除器，该消除器实现高通滤波器以抑制低多普勒频移的回波。通过MTI脉冲消除器传递接收信号会引入噪声样本之间的相关性。这反过来又减少了可用于积分的独立噪声样本的总数，从而导致MTI噪声相关性损失。此外，MTI 消除器显着抑制速度接近其频率响应零点的目标，从而导致额外的 MTI 速度响应损失。假设使用 2 脉冲消除器，计算 MTI 损耗的这两个分量。

m = 2;
[Lmti_a, Lmti_b] = mtiloss(Pd,Pfa,N,m,'Swerling1')
Lmti_a = 1.4468
Lmti_b = 8.1562

在使用单个PRF的系统中，对于所需的高检测概率，MTI速度响应损失可能非常高。为了消除这种损失，PRF分集几乎总是用于真正的雷达系统。

二元累计

二元累计是一种次优非相干积分技术，也称为 M-of-N 积分。如果M出N接收到的脉冲超过预定阈值，则声明存在目标。二进制积分器是一种相对简单的自动检测器，对可能与目标回波一起存在的单个大干扰脉冲的影响不太敏感。因此，当背景噪声或杂波为非高斯时，二元积分器更可靠。由于二元积分是一种次优技术，因此与最优非相干积分相比，它会导致二元积分损失。的最优值M不是一个敏感的选择，它可能与最优值有很大不同，而不会产生明显的损失，导致二进制积分损耗低于1.4 dB。计算二进制积分损耗N是 10 和M设置为 6。

M = 6;
Lbint = binaryintloss(Pd,Pfa,N,M)
Lbint = 1.0549

该函数计算假设目标稳定（Swerling 0）的损失。由于波动损耗包含在可检测性因子中，因此在波动目标的情况下可以使用相同的二元积分损耗计算。binaryintloss

CFAR

恒定误报率（CFAR）检测器用于在噪声或干扰水平变化时保持近似恒定的误报率。由于CFAR对有限数量的参考单元进行平均来估计噪声水平，因此估计值会受到误差的影响，从而导致CFAR损失。与具有已知噪声电平的固定阈值相比，CFAR损耗是指在噪声电平未知的情况下，使用CFAR实现所需检测性能所需的信噪比增加。假设总共 120 个单元用于单元平均 CFAR，则计算 CFAR 损失。

Nrc = 120;
Lcfar = cfarloss(Pfa,Nrc)
Lcfar = 0.2500

有效可检测性因子

扫描和信号处理损耗增加了可检测性系数，这意味着需要更多的能量来进行检测。由此产生的可检测性因子（包括所有这些损失的影响）称为有效可检测性因子。使用该函数创建瀑布图，显示计算扫描和信号处理损耗对可检测性因子的综合影响。

D = [D0 -Gi Lf Lmti_a+Lmti_b Lbint Lcfar Larray Lb];
helperDetectabilityWaterfallPlot(D, {'Single-pulse steady target','Pulse integration gain','Fluctuation loss'...
    'MTI loss', 'Binary integration loss', 'CFAR loss', 'Scan sector loss', 'Beam shape loss'});
title('Detectability Factor')

由此产生的有效可检测性因子等于28.42 dB。如果将扫描和信号处理损耗考虑在内，所需的信噪比将增加近15 dB。分析表明，该系统实际上无法满足检测 1RCS 目标在 100 公里处的检测概率需求

radarmetricplot(R*1e-3,SNR,sum(D), ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC, Eclipsing, Scanning and Signal Processing Losses)'}])
legend('Location','best')
ylim([-10 30]);

这个问题可以通过增加可用的信噪比或降低所需的信噪比来解决。传输更多功率或增加天线增益会提高可用的信噪比，而增加积分时间会降低所需的信噪比。但是，在某些应用中，系统参数的子集可能会受到其他要求的约束，因此无法更改。例如，如果对现有系统执行分析，则增加可用信噪比可能不是一种选择。在这种情况下，对信号处理链进行调整以降低可检测性因子可能是一个可接受的解决方案。

为了降低所需的信噪比，在以下各节中，我们假设脉冲数N从 10 增加到 40。

此外，我们可以更改对最大范围和检测概率的要求。可以定义一对Objective和Threshold值，而不是指定所需检测概率或最大范围的单个数字。客观需求描述了完全满足任务需要所需的系统的期望性能水平。阈值要求描述了系统的最低可接受性能水平。使用一对值而不是单个值来定义需求为设计提供了更大的灵活性，并为选择系统参数创建了权衡空间。

假设Pd为 0.9，并将值设置为 0.8。同样，最大距离仍为 100 公里，而该值设置为 90 公里。现在计算了目标和阈值Pd可检测性因子

N = 40;
M = 18;
Pd = [0.9 0.8];

[Lmti_a, Lmti_b] = mtiloss(Pd,Pfa,N,m,'Swerling1');
Dx = detectability(Pd,Pfa,N,'Swerling1') + cfarloss(Pfa,Nrc) + beamloss ...
    + Lmti_a + Lmti_b + binaryintloss(Pd,Pfa,N,M) + arrayscanloss(Pd,Pfa,N,theta,'Swerling1')
Dx = 2×1

   24.2522
   18.0494

Rm = [100e3 90e3];
radarmetricplot(R*1e-3,SNR,Dx(1),Dx(2), ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(N=40)'}])
legend('Location','best')
ylim([-10 30]);

SNR 与范围的关系图现在有一个黄色的警告区域，指示 SNR 值和目标范围，其中系统的性能介于目标和阈值之间。我们可以看到，该系统最多约 70 公里，70到100km虽然满足阈值要求但是违反了Pd的客观要求

有效检测概率

信噪比与距离图显示，雷达系统的探测性能随距离而变化。距离在70以下的目标，检测概率大于或等于 0.9，而在 70 公里和 100 公里之间，它将被检测到Pd至少 0.8。由于一些考虑的损失取决于检测的概率，因此实际Pd在探测器上，输出随范围而变化。我们可以使用 ROC 曲线来计算Pd作为范围的函数。

% Generate a vector of probability values at which to compute the ROC curve
p = probgrid(0.1,0.9999,100);

% Compute the required SNR at these probabilities
[lmti_a, lmti_b] = mtiloss(p,Pfa,N,m,'Swerling1');
dx = detectability(p,Pfa,N,'Swerling1') + cfarloss(Pfa,Nrc) + beamloss ...
    + lmti_a + lmti_b + binaryintloss(p,Pfa,N,M) + arrayscanloss(p,Pfa,N,theta,'Swerling1');

% Plot the ROC curve
helperRadarPdVsSNRPlot(dx,p,[0.1 0.9999]);

现在可以通过可用SNR值差值此处ROC曲线来计算探测器输出端的有效检测概率

% Interpolate the ROC curve at the available SNR
Pdeff = rocinterp(dx,p,SNR,'snr-pd');

% Plot the effective Pd as a function of range
radarmetricplot(R*1e-3,Pdeff,Pd(1),Pd(2), ...
    'MetricName','Effective P_d', ...
    'RequirementName','P_d', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
legend('Location','best')
ylim([0.5 1.0])

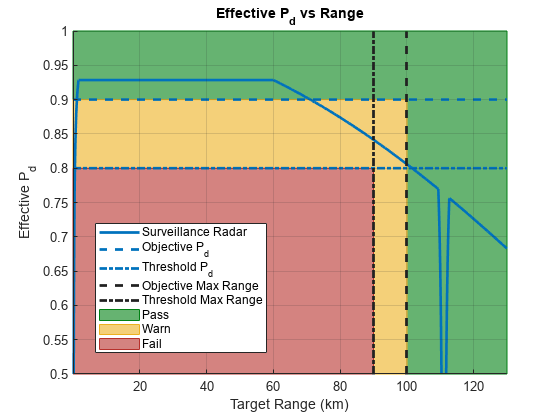
结果表明，由于STC的应用，在2 km至60 km的范围内，检测概率几乎是恒定的。对于具有 1 m² 的目标,它高于 0.92。在 70 公里和 87 公里之间的有效范围内Pd高于 0.85。在最大探测距离要求的值下，检测到的概率约为0.84，在100 km的范围内略高于0.8。

总结

此示例显示了各种损耗如何影响雷达系统的探测性能。它从雷达方程开始，介绍了可用信噪比和可探测因子的概念。以监视雷达系统为例，它显示了可用的信噪比如何通过STC和波束减小，而可探测因子如何通过扫描和信号处理损耗而增加。最后，该示例演示了如何计算不同目标范围的接收机输出处的有效检测概率。

完整项目代码

%%
% 仿真雷达探测目标能力

% 仿真目标及雷达参数
lambda = freq2wavelen(3e9);         % Wavelength (m)
Pt = 0.2e6;                         % Peak power (W)
tau = 1.1e-5;                       % Pulse width (s)
G = 34;                             % Transmit and receive antenna gain (dB)
Ts = systemp(4.1);                  % System temperature (K) 
rcs = 1;                            % Target radar cross section (m^2)
Rm = 100e3;                         % Required maximum range (m)

%% 无损失下雷达可用SNR
L = 0;                              % Combined transmission line and propagation losses (dB)
R = (1:40:130e3).';                 % Range samples (m)
SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'Loss',L);

%100m的可用SNR
SNRatRm = SNR(find(R>=Rm,1))
%绘制最大探测范围内的可用SNR
radarmetricplot(R*1e-3,SNR,'MetricName','Available SNR','MaxRangeRequirement',Rm*1e-3,...
    'RangeUnit','km','MetricUnit','dB','RadarName',{'Surveillance Radar'});
legend('Location','best');


%所需SNR
%pd是检测概率、pfa是误报率，比较不同Swerling来指定可检测因子
Pd = 0.9;
Pfa = 1e-6;
D0 = detectability(Pd,Pfa,1,'Swerling0')
D1 = detectability(Pd,Pfa,1,'Swerling1')
% 在对脉冲进行非相干积分后
N = 10;
DN = detectability(Pd,Pfa,N,'Swerling1')

% 积分增益
Gi = detectability(Pd,Pfa,1,'Swerling0') - detectability(Pd,Pfa,N,'Swerling0')
% 波动损耗
Lf = detectability(Pd,Pfa,N,'Swerling1') - detectability(Pd,Pfa,N,'Swerling0')
% 可检测性因子

helperDetectabilityWaterfallPlot([D0 -Gi Lf], {'Single-pulse steady target','Pulse integration gain','Fluctuation loss'});
title('Detectability Factor')


%%
% 绘制雷达监测性能
radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(No Losses)'}]);
legend('Location','best');



%%
% 距离相关因素
Rmin = time2range(tau)

prf = 1350;                         % Pulse repetition frequency
Rua = time2range(1/prf)
Rua = 1.1103e+05

%考虑遮挡因子影响
Du = tau*prf;                       % Duty cycle
Fecl = eclipsingfactor(R,Du,prf);   % Eclipsing factor

SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'CustomFactor',Fecl,'Loss', L);

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With Eclipsing)'}]);
legend('Location','best');

%%
%灵敏度时间控制
Rstc = 60e3;                        % STC cutoff range (m)
Xstc = 4;                           % STC exponent selected to maintain target detectability at ranges below Rstc (since the signal power is inversely proportional to R^4)
Fstc = stcfactor(R,Rstc,Xstc);      % STC factor

SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'CustomFactor',Fecl+Fstc,'Loss',L);

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC and Eclipsing for 1 m^2 Target)'}]);
legend('Location','best');
ylim([-30 30])


%%
% 拒绝微小干扰
SNRsmallRCS = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',0.03,'CustomFactor',Fecl+Fstc,'Loss',L);

radarmetricplot(R*1e-3,SNRsmallRCS,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC and Eclipsing for 0.03 m^2 Target)'}]);
legend('Location','best');
ylim([-30 20])


%%
% 波束损失
Lb = beamloss

beamloss(true)
theta = [-60 60];
Larray = arrayscanloss(Pd,Pfa,N,theta,'Swerling1')


%%
% 信号处理
m = 2;
[Lmti_a, Lmti_b] = mtiloss(Pd,Pfa,N,m,'Swerling1')


%%
% 二元累计
M = 6;
Lbint = binaryintloss(Pd,Pfa,N,M)
Lbint = 1.0549

%%
% cafr
Nrc = 120;
Lcfar = cfarloss(Pfa,Nrc)

%%
D = [D0 -Gi Lf Lmti_a+Lmti_b Lbint Lcfar Larray Lb];
helperDetectabilityWaterfallPlot(D, {'Single-pulse steady target','Pulse integration gain','Fluctuation loss'...
    'MTI loss', 'Binary integration loss', 'CFAR loss', 'Scan sector loss', 'Beam shape loss'});
title('Detectability Factor')


%%
%有效可检测因子
N = 40;
M = 18;
Pd = [0.9 0.8];

[Lmti_a, Lmti_b] = mtiloss(Pd,Pfa,N,m,'Swerling1');
Dx = detectability(Pd,Pfa,N,'Swerling1') + cfarloss(Pfa,Nrc) + beamloss ...
    + Lmti_a + Lmti_b + binaryintloss(Pd,Pfa,N,M) + arrayscanloss(Pd,Pfa,N,theta,'Swerling1')

Rm = [100e3 90e3];
radarmetricplot(R*1e-3,SNR,Dx(1),Dx(2), ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(N=40)'}])
legend('Location','best')
ylim([-10 30]);

%%
%有效检测概率
% Generate a vector of probability values at which to compute the ROC curve
p = probgrid(0.1,0.9999,100);

% Compute the required SNR at these probabilities
[lmti_a, lmti_b] = mtiloss(p,Pfa,N,m,'Swerling1');
dx = detectability(p,Pfa,N,'Swerling1') + cfarloss(Pfa,Nrc) + beamloss ...
    + lmti_a + lmti_b + binaryintloss(p,Pfa,N,M) + arrayscanloss(p,Pfa,N,theta,'Swerling1');

% Plot the ROC curve
helperRadarPdVsSNRPlot(dx,p,[0.1 0.9999]);


%%
% Interpolate the ROC curve at the available SNR
Pdeff = rocinterp(dx,p,SNR,'snr-pd');

% Plot the effective Pd as a function of range
radarmetricplot(R*1e-3,Pdeff,Pd(1),Pd(2), ...
    'MetricName','Effective P_d', ...
    'RequirementName','P_d', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
legend('Location','best')
ylim([0.5 1.0])