机器学习算法-线性回归

最新推荐文章于 2024-04-29 11:00:38 发布

私の未来は夢じゃない

最新推荐文章于 2024-04-29 11:00:38 发布

阅读量628

点赞数 3

文章标签： python 逻辑回归机器学习人工智能深度学习

本文链接：https://blog.csdn.net/weixin_45064713/article/details/108352844

版权

线性回归的概念

1、线性回归的原理

2、线性回归损失函数、代价函数、目标函数

3、优化方法(梯度下降法、牛顿法、拟牛顿法等)

4、线性回归的评估指标

5、sklearn参数详解

一、回归

回归是一种预测建模技术，其中被估计的目标变量是连续的。回归应用的例子包括使用其他经济学指标预测股市指数，基于高空气特征流预测一个地区的降水量，根据广告开销预测公司的总销售，按照有机物质中的碳14残留估计化石的年龄。

1、线性回归的原理

这是一家房产网的数据，可以看到有房价、面积、厅室的数据：

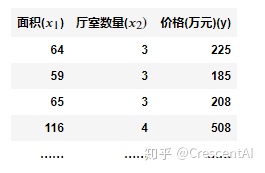
我们可以将价格和面积、厅室数量的关系习得为

$f(x)=\theta_0+\theta_1x_1+\theta_2x_2$ ，使得

$f(x)\approx y$ ，这就是一个直观的线性回归的样式。

2、线性回归的一般形式

给定由d个属性描述的实例

$x=(x1;x2;...;xd)$ ,其中

$xi$ 是

$x$ 在第

$i$ 个属性上的取值，线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数

$f(x)=w1x1+w2x2+...+wdxd+b$ 一般用向量的形式写成

$f(x)=wTx+b$ ，其中

$w=(w1;w2;...;wd)$

$w$ 和

$b$ 学得之后，模型就得以确定。

3、线性回归

给定数据集

$D=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$ ,其中,

$x_i = (x_{i1};x_{i2};x_{i3};...;x_{id})$ ，

$y_i\in R$ ，其中n表示变量的数量，d表示每个变量的维度。“线性回归”（linear regression）试图学得一个现行模型以尽可能准确地预测实值输出标记。

可以用以下函数来描述y和x之间的关系：

$\begin{align*} f(x) &= \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_dx_d \\ &= \sum_{i=0}^{d}\theta_ix_i \\ \end{align*}$

如何来确定的值，使得 ( )尽可能接近y的值呢？均方误差是回归中常用的性能度量，即：

$J(\theta)=\frac{1}{2}\sum_{j=1}^{n}(h_{\theta}(x^{(i)})-y^{(i)})^2$

4、极大似然估计（概率角度的诠释）

下面我们用极大似然估计，来解释为什么要用均方误差作为性能度量，我们可以把目标值和变量写成如下等式：

$y^{(i)} = \theta^T x^{(i)}+\epsilon^{(i)}$

$\epsilon$ 表示我们未观测到的变量的印象，即随机噪音。我们假定

$\epsilon$ 是独立同分布，服从高斯分布。（根据中心极限定理）

$p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}\right)$

因此，

$p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2}\right)$

我们建立极大似然函数，即描述数据遵从当前样本分布的概率分布函数。由于样本的数据集独立同分布，因此可以写成

$L(\theta) = p(\vec y | X;\theta) = \prod^n_{i=1}\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2}\right)$

选择

$\theta$ ，使得似然函数最大化，这就是极大似然估计的思想。为了方便计算，我们计算时通常对对数似然函数求最大值：

$\begin{align*} l(\theta) &= log L(\theta) = log \prod^n_{i=1}\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2} {2\sigma^2}\right) \\ & = \sum^n_{i=1}log\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2}\right) \\ & = nlog\frac{1}{{\sqrt{2\pi}\sigma}} - \frac{1}{\sigma^2} \cdot \frac{1}{2}\sum^n_{i=1}((y^{(i)}-\theta^T x^{(i)})^2 \end{align*}$

显然，最大化

$( )$ 即最小化

$\frac{1}{2}\sum^n_{i=1}((y^{(i)}-\theta^T x^{(i)})^2$ 。

这一结果即均方误差，因此用这个值作为代价函数来优化模型在统计学的角度是合理的。

二、线性回归损失函数、代价函数、目标函数

损失函数(Loss Function)：度量单样本预测的错误程度，损失函数值越小，模型就越好。
代价函数(Cost Function)：度量全部样本集的平均误差。
目标函数(Object Function)：代价函数和正则化函数，最终要优化的函数。

常用的损失函数包括：0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等；常用的代价函数包括均方误差、均方根误差、平均绝对误差等。

思考题：既然代价函数已经可以度量样本集的平均误差，为什么还要设定目标函数？

回答：

当模型复杂度增加时，有可能对训练集可以模拟的很好，但是预测测试集的效果不好，出现过拟合现象，这就出现了所谓的“结构化风险”。结构风险最小化即为了防止过拟合而提出来的策略，定义模型复杂度为

$J(F)$ ，目标函数可表示为：

$\underset{f\in F}{min}\, \frac{1}{n}\sum^{n}_{i=1}L(y_i,f(x_i))+\lambda J(F)$

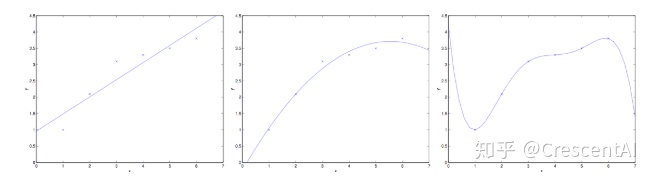
例如有以上6个房价和面积关系的数据点，可以看到，当设定

$f(x)=\sum_{j=0}^{5}\theta_jx_j$ 时，可以完美拟合训练集数据，但是，真实情况下房价和面积不可能是这样的关系，出现了过拟合现象。当训练集本身存在噪声时，拟合曲线对未知影响因素的拟合往往不是最好的。通常，随着模型复杂度的增加，训练误差会减少；但测试误差会先增加后减小。我们的最终目的时试测试误差达到最小，这就是我们为什么需要选取适合的目标函数的原因。

三、线性回归的优化方法

3.1 最小二乘法

现在问题转换成了求解让

$SSE$

最⼩化的参数向量

$w$

，这种通过最⼩化真实值和预测值之间

$SSE$

的来求解参数的方法叫做最⼩二乘法。

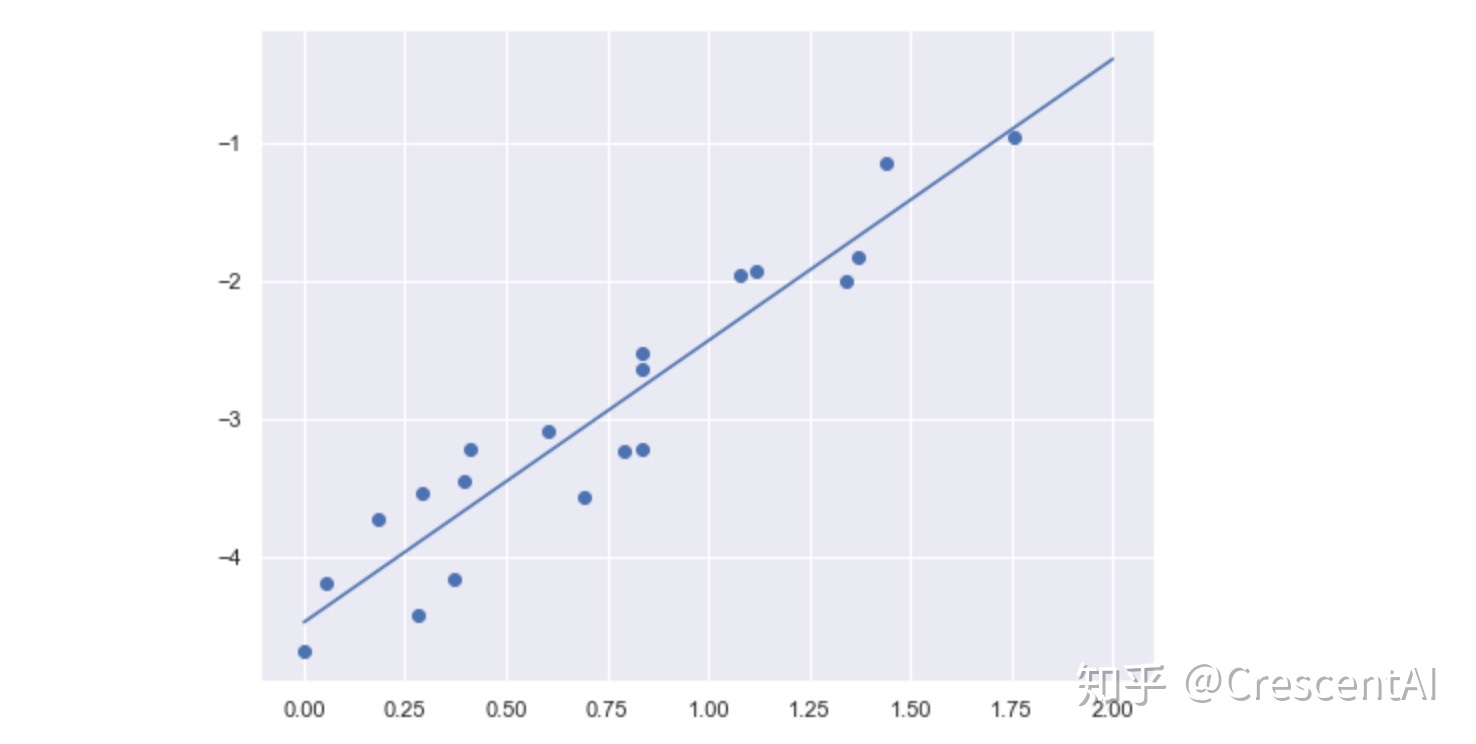
3.1.1 ⼀元线性回归的求解过程

⾸首先我们对上图的数据进⾏行行拟合，可得到：

3.1.2 多元线性回归求解参数

3.1.3 最小二乘法矩阵求解

令

$X = \left[ \begin{array} {cccc} (x^{(1)})^T\\ (x^{(2)})^T\\ \ldots \\ (x^{(n)})^T \end{array} \right]$

其中，

$x^{(i)} = \left[ \begin{array} {cccc} x_1^{(i)}\\ x_2^{(i)}\\ \ldots \\ x_d^{(i)} \end{array} \right]$

由于

$Y = \left[ \begin{array} {cccc} y^{(1)}\\ y^{(2)}\\ \ldots \\ y^{(n)} \end{array} \right]$

$h_\theta(x)$ 可以写作

$h_\theta(x)=X\theta$

对于向量来说，有

$z^Tz = \sum_i z_i^2$

因此可以把损失函数写作

$J(\theta)=\frac{1}{2}(X\theta-Y)^T(X\theta-Y)$

为最小化

$( )$ ,对

求导可得：

$\begin{align*} \frac{\partial{J(\theta)}}{\partial\theta} &= \frac{\partial}{\partial\theta} \frac{1}{2}(X\theta-Y)^T(X\theta-Y) \\ &= \frac{1}{2}\frac{\partial}{\partial\theta} (\theta^TX^TX\theta - Y^TX\theta-\theta^T X^TY - Y^TY) \\ \end{align*}$

中间两项互为转置，由于求得的值是个标量，矩阵与转置相同，因此可以写成

$\begin{align*} \frac{\partial{J(\theta)}}{\partial\theta} &= \frac{1}{2}\frac{\partial}{\partial\theta} (\theta^TX^TX\theta - 2\theta^T X^TY - Y^TY) \\ \end{align*}$

令偏导数等于零，由于最后一项和

无关，偏导数为0。

因此，

$\frac{\partial{J(\theta)}}{\partial\theta} = \frac{1}{2}\frac{\partial}{\partial\theta} \theta^TX^TX\theta - \frac{\partial}{\partial\theta} \theta^T X^TY$

利用矩阵求导性质，

$\frac{\partial \vec x^T\alpha}{\partial \vec x} =\alpha$ 和

$\frac{\partial A^TB}{\partial \vec x} = \frac{\partial A^T}{\partial \vec x}B + \frac{\partial B^T}{\partial \vec x}A$

$\begin{align*} \frac{\partial}{\partial\theta} \theta^TX^TX\theta &= \frac{\partial}{\partial\theta}{(X\theta)^TX\theta}\\ &= \frac{\partial (X\theta)^T}{\partial\theta}X\theta + \frac{\partial (X\theta)^T}{\partial\theta}X\theta \\ &= 2X^TX\theta \end{align*}$

$\frac{\partial{J(\theta)}}{\partial\theta} = X^TX\theta - X^TY$

令导数等于零，

$X^TX\theta = X^TY$

$\theta = (X^TX)^{(-1)}X^TY$

3.2 梯度下降法

设定初始参数

,不断迭代，使得

$( )$ 最小化：

$\theta_j:=\theta_j-\alpha\frac{\partial{J(\theta)}}{\partial\theta}$

$\begin{align*} \frac{\partial{J(\theta)}}{\partial\theta} &= \frac{\partial}{\partial\theta_j}\frac{1}{2}\sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})^2 \\ &= 2*\frac{1}{2}\sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})*\frac{\partial}{\partial\theta_j}(f_\theta(x)^{(i)}-y^{(i)}) \\ &= \sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})*\frac{\partial}{\partial\theta_j}(\sum_{j=0}^{d}\theta_jx_j^{(i)}-y^{(i)}))\\ &= \sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})x_j^{(i)} \\ \end{align*}$

即：

$\theta_j = \theta_j + \alpha\sum_{i=1}^{n}(y^{(i)}-f_\theta(x)^{(i)})x_j^{(i)}$

注：下标j表示第j个参数，上标i表示第i个数据点。

将所有的参数以向量形式表示，可得：

$\theta = \theta + \alpha\sum_{i=1}^{n}(y^{(i)}-f_\theta(x)^{(i)})x^{(i)}$

由于这个方法中，参数在每一个数据点上同时进行了移动，因此称为批梯度下降法，对应的，我们可以每一次让参数只针对一个数据点进行移动，即：

$\theta = \theta + \alpha(y^{(i)}-f_\theta(x)^{(i)})x^{(i)}$

这个算法成为随机梯度下降法，随机梯度下降法的好处是，当数据点很多时，运行效率更高；缺点是，因为每次只针对一个样本更新参数，未必找到最快路径达到最优值，甚至有时候会出现参数在最小值附近徘徊而不是立即收敛。但当数据量很大的时候，随机梯度下降法经常优于批梯度下降法。

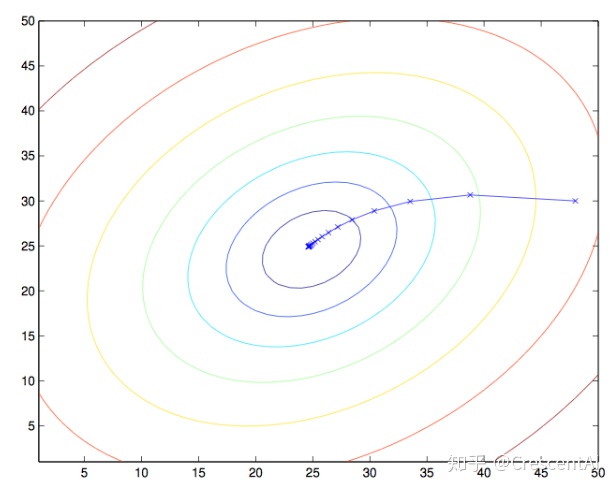
当J为凸函数时，梯度下降法相当于让参数 θ不断向J的最小值位置移动，梯度下降法的缺陷：如果函数为非凸函数，有可能找到的并非全局最优值，而是局部最优值。

3.3 牛顿法

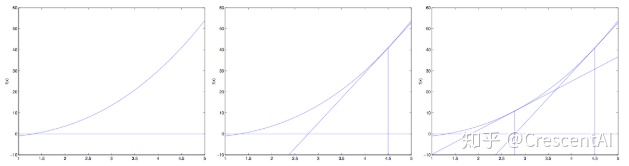
通过图例可知(参考吴恩达CS229),

$f(\theta)' = \frac{f(\theta)}{\Delta},\Delta = \theta_0 - \theta_1$

可求得，

$\theta_1 = \theta_0 - \frac {f(\theta_0)}{f(\theta_0)'}$

重复迭代，可以让逼近取到

$( )$ 的最小值

当我们对损失函数

$( )$ 进行优化的时候，实际上是想要取到

$′( )$ 的最小值，因此迭代公式为：

$\theta :=\theta-\frac{l'(\theta)}{l''(\theta)}$

当

$\theta$ 是向量值的时候，

$\theta :=\theta - H^{-1}\Delta_{\theta}l(\theta)$

其中，

$Δ ( )$ 是

$( )$ 对

的偏导数，

是

$( )$ 的海森矩阵，

$H_{ij} = \frac{\partial ^2l(\theta)}{\partial\theta_i\partial\theta_j}$

Answer：将

$( )$ 用泰勒公式展开到第二阶，

$f(x) = f(x_0) + f'(x_0)(x - x_0)+\frac{1}{2}f''(x_0)(x - x_0)^2$

对上式求导，并令导数等于0，求得x值

$f'(x) = f'(x_0) + f''(x_0)x -f''(x_0)x_0 = 0$

可以求得，

$x = x_0 - \frac{f'(x_0)}{f''(x_0)}$

牛顿法的收敛速度非常快，但海森矩阵的计算较为复杂，尤其当参数的维度很多时，会耗费大量计算成本。我们可以用其他矩阵替代海森矩阵，用拟牛顿法进行估计。

3.4 拟牛顿法

拟牛顿法的思路是用一个矩阵替代计算复杂的海森矩阵H，因此要找到符合H性质的矩阵。
要求得海森矩阵符合的条件，同样对泰勒公式求导

$f'(x) = f'(x_0) + f''(x_0)x -f''(x_0)x_0$

令

$= 1$ ，即迭代后的值，代入可得：

更一般的，

$f'(x_{k+1}) = f'(x_k) + f''(x_k)x_{k+1} - f''(x_k)x_k$

$f'(x_{k+1}) - f'(x_k) = f''(x_k)(x_{k+1}- x_k)= H(x_{k+1}- x_k)$

为第k个迭代值

即找到矩阵G，使得它符合上式。常用的拟牛顿法的算法包括DFP，BFGS等，作为选学内容，有兴趣者可自行查询材料学习。

四、线性回归的评估指标

均方误差(MSE)：

$\frac{1}{m}\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2$

均方根误差(RMSE)：

$\sqrt{MSE} = \sqrt{\frac{1}{m}\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2}$

平均绝对误差(MAE)：

$\frac{1}{m}\sum^{m}_{i=1} | (y^{(i)} - \hat y^{(i)} |$

但以上评价指标都无法消除量纲不一致而导致的误差值差别大的问题，最常用的指标是

$2$ ,可以避免量纲不一致问题

$R^2: = 1-\frac{\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2}{\sum^{m}_{i=1}(\bar y - \hat y^{(i)})^2} =1-\frac{\frac{1}{m}\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2}{\frac{1}{m}\sum^{m}_{i=1}(\bar y - \hat y^{(i)})^2} = 1-\frac{MSE}{VAR}$

我们可以把

$2$ 理解为，回归模型可以成功解释的数据方差部分在数据固有方差中所占的比例，

$2$ 越接近1，表示可解释力度越大，模型拟合的效果越好。

五、sklearn.linear_model参数详解：

fit_intercept : 默认为True,是否计算该模型的截距。如果使用中心化的数据，可以考虑设置为False,不考虑截距。注意这里是考虑，一般还是要考虑截距
normalize: 默认为false. 当fit_intercept设置为false的时候，这个参数会被自动忽略。如果为True,回归器会标准化输入参数：减去平均值，并且除以相应的二范数。当然啦，在这里还是建议将标准化的工作放在训练模型之前。通过设置sklearn.preprocessing.StandardScaler来实现，而在此处设置为false
copy_X : 默认为True, 否则X会被改写
n_jobs: int 默认为1. 当-1时默认使用全部CPUs ??(这个参数有待尝试)

可用属性：
coef_:训练后的输入端模型系数，如果label有两个，即y值有两列。那么是一个2D的array
intercept_: 截距

可用的methods:
fit(X,y,sample_weight=None): X: array, 稀疏矩阵 [n_samples,n_features] y: array [n_samples, n_targets] sample_weight: 权重 array [n_samples] 在版本0.17后添加了sample_weight
get_params(deep=True)： 返回对regressor 的设置值
predict(X): 预测 基于 R^2值
score： 评估

参考:

API详解:sklearn.linear_model.LinearRegression_人工智能_Sehr Gut-CSDN博客

六、代码实现

6.1 生成数据

#生成数据
import numpy as np
#生成随机数
np.random.seed(1234)
x = np.random.rand(500,3)
#构建映射关系，模拟真实的数据待预测值,映射关系为y = 4.2 + 5.7*x1 + 10.8*x2，可自行设置值进行尝试
y = x.dot(np.array([4.2,5.7,10.8]))

1、先尝试调用sklearn的线性回归模型训练数据

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline

# 调用模型
lr = LinearRegression(fit_intercept=True)
# 训练模型
lr.fit(x,y)
print("估计的参数值为：%s" %(lr.coef_))
# 计算R平方
print('R2:%s' %(lr.score(x,y)))
# 任意设定变量，预测目标值
x_test = np.array([2,4,5]).reshape(1,-1)
y_hat = lr.predict(x_test)
print("预测值为: %s" %(y_hat))

估计的参数值为：[ 4.2 5.7 10.8]
R2:1.0
预测值为: [85.2]

2、最小二乘法的矩阵求解

class LR_LS():
    def __init__(self):
        self.w = None      
    def fit(self, X, y):
        # 最小二乘法矩阵求解
        #============================= show me your code =======================
        self.w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
        #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        #============================= show me your code =======================
        y_pred = X.dot(self.w)
        #============================= show me your code =======================
        return y_pred

if __name__ == "__main__":
    lr_ls = LR_LS()
    lr_ls.fit(x,y)
    print("估计的参数值：%s" %(lr_ls.w))
    x_test = np.array([2,4,5]).reshape(1,-1)
    print("预测值为: %s" %(lr_ls.predict(x_test)))

估计的参数值：[ 4.2 5.7 10.8]
预测值为: [85.2]

3、梯度下降法

class LR_GD():
    def __init__(self):
        self.w = None     
    def fit(self,X,y,alpha=0.02,loss = 1e-10): # 设定步长为0.002,判断是否收敛的条件为1e-10
        y = y.reshape(-1,1) #重塑y值的维度以便矩阵运算
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros((d)) #将参数的初始值定为0
        tol = 1e5
        #============================= show me your code =======================
        while tol > loss:
            h_f = X.dot(self.w).reshape(-1,1) 
            theta = self.w + alpha*np.mean(X*(y - h_f),axis=0) #计算迭代的参数值
            tol = np.sum(np.abs(theta - self.w))
            self.w = theta
        #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lr_gd = LR_GD()
    lr_gd.fit(x,y)
    print("估计的参数值为：%s" %(lr_gd.w))
    x_test = np.array([2,4,5]).reshape(1,-1)
    print("预测值为：%s" %(lr_gd.predict(x_test)))

估计的参数值为：[ 4.20000001 5.70000003 10.79999997]
预测值为：[85.19999995]

6.2 房屋数据集

# 加利福尼亚数据集
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing as fch
housevalue = fch()
X = pd.DataFrame(housevalue.data)
X.head()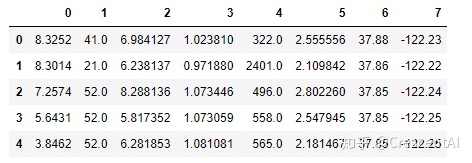

y = housevalue.target
y

array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])

housevalue.feature_names

['MedInc',
'HouseAge',
'AveRooms',
'AveBedrms',
'Population',
'AveOccup',
'Latitude',
'Longitude']

Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
reg = LinearRegression().fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)

0.6043668160178817

rid = Ridge(alpha=1).fit(Xtrain,Ytrain)
rid.score(Xtest,Ytest)

0.6043610352312279

las = Lasso(alpha=0.1).fit(Xtrain,Ytrain)
las.score(Xtest,Ytest)

0.5368702511716803

# 交叉验证,对比线性回归和岭回归结果的变化
alpharange = np.arange(1,1001,100)
ridge=[]
lr = []
for i in alpharange:
    reg = Ridge(alpha=i)
    l = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring='r2').mean()
    ls = cross_val_score(l,X,y,cv=5,scoring='r2').mean()
    ridge.append(regs)
    lr.append(ls)

plt.plot(alpharange,ridge,color='red',label='Ridge')
plt.plot(alpharange,lr,color='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()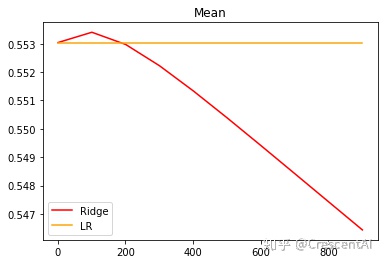

alpharange = np.arange(1,201,10)
ridge=[]
lr = []
for i in alpharange:
    reg = Ridge(alpha=i)
    l = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring='r2').mean()
    ls = cross_val_score(l,X,y,cv=5,scoring='r2').mean()
    ridge.append(regs)
    lr.append(ls)

plt.plot(alpharange,ridge,color='red',label='Ridge')
plt.plot(alpharange,lr,color='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()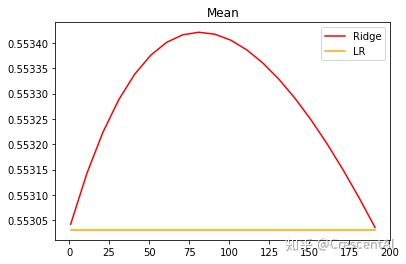

alpharange = np.arange(1,1001,100)
ridge=[]
lr = []
for i in alpharange:
    reg = Ridge(alpha=i)
    l = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring='r2').var()
    ls = cross_val_score(l,X,y,cv=5,scoring='r2').var()
    ridge.append(regs)
    lr.append(ls)

plt.plot(alpharange,ridge,color='red',label='Ridge')
plt.plot(alpharange,lr,color='orange',label='LR')
plt.title('ValueError')
plt.legend()
plt.show()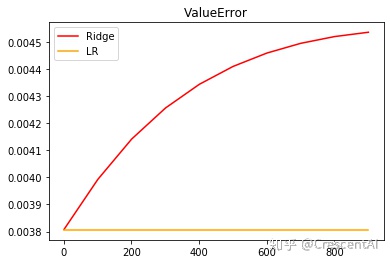

from sklearn.datasets import load_boston
X = load_boston().data
y = load_boston().target
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
alpharange = np.arange(1,1001,100)
ridge=[]
lr = []
for i in alpharange:
    reg = Ridge(alpha=i)
    l = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring='r2').mean()
    ls = cross_val_score(l,X,y,cv=5,scoring='r2').mean()
    ridge.append(regs)
    lr.append(ls)

plt.plot(alpharange,ridge,color='red',label='Ridge')
plt.plot(alpharange,lr,color='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()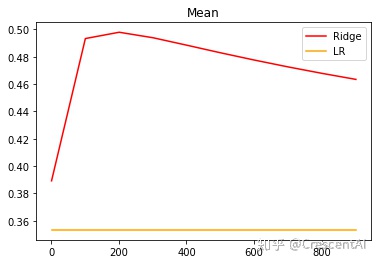

alpharange = np.arange(1,1001,100)
ridge=[]
lr = []
for i in alpharange:
    reg = Ridge(alpha=i)
    l = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring='r2').var()
    ls = cross_val_score(l,X,y,cv=5,scoring='r2').var()
    ridge.append(regs)
    lr.append(ls)

plt.plot(alpharange,ridge,color='red',label='Ridge')
plt.plot(alpharange,lr,color='orange',label='LR')
plt.title('ValueError')
plt.legend()
plt.show()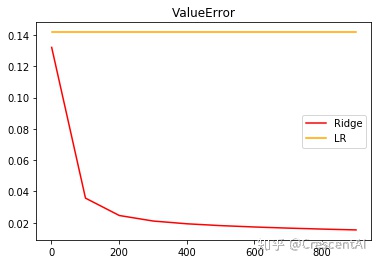

局部加权限线性回归

$w =(X^TWX) ^ {-1}X^TWy$

核可以自由选择,最常用的高斯核,高斯核对应的权重:

$w(ii)=exp[\frac{|x^i-x|^2}{-2k^2}]$

xi距离x距离越小,w越大,k决定群众的大小
k越大,权重的差距越小;k越小,权重的差距越大

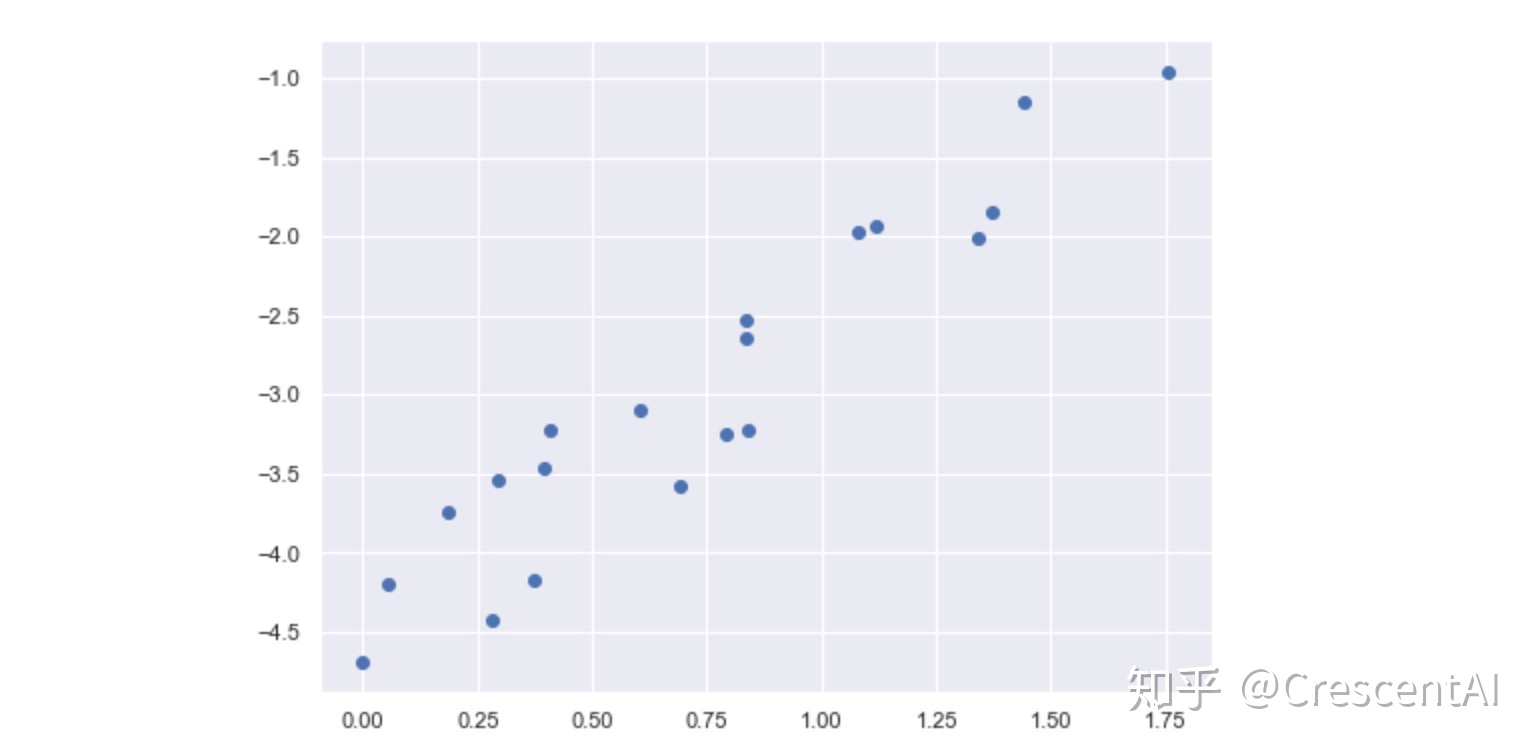
ex0 = pd.read_csv('ex0.txt',sep='\t',header=None)
ex0.head()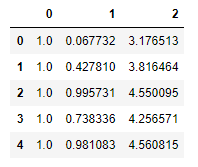

xMat = np.mat(ex0.iloc[:,:-1].values)
yMat = np.mat(ex0.iloc[:,-1].values).T
plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5)
plt.show()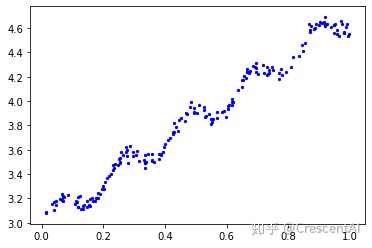

standRegres(ex0)
matrix([[3.00774324],
        [1.69532264]])
plt.scatter(xMat.A[:,1],yMat.A,c='b',s=5)
ws = standRegres(ex0)
yhat = xMat*ws
plt.plot(xMat[:,1],yhat,c='r')
plt.show()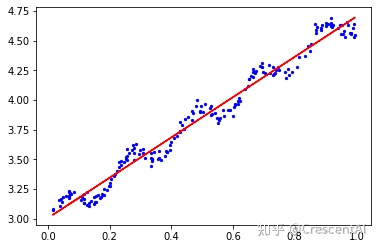

def LWLR(testMat,xMat,yMat,k=1.0):
    n = testMat.shape[0]
    m = xMat.shape[0]
    weights = np.mat(np.eye(m))
    yhat = np.zeros(n)
    for i in range(n):
        for j in range(m):
            diffMat = testMat[i]-xMat[j]
            weights[j,j] = np.exp(diffMat*diffMat.T/(-2*k**2))
        xTx = xMat.T*(weights*xMat)
        if np.linalg.det(xTx)==0:
            print('矩阵为奇异矩阵,不能求逆')
            return
        ws = xTx.I*(xMat.T*(weights*yMat))
        yhat[i]=testMat[i]*ws
    return ws,yhat
# 将数据点排列,返回索引
srt = xMat[:,1].argsort(0)
srt

matrix([[151],
.......
[ 2]], dtype=int64)

xSort = xMat[srt][:,0]
# 不同取值下的yhat
ws1,yhat1 = LWLR(xMat,xMat,yMat,k=1.0)
ws2,yhat2 = LWLR(xMat,xMat,yMat,k=0.01)
ws3,yhat3 = LWLR(xMat,xMat,yMat,k=0.003)

fig = plt.figure(figsize=(6,8),dpi=100)
# 子图1(欠拟合)
fig1 = fig.add_subplot(311)
plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2)
plt.plot(xSort[:,1],yhat1[srt],color='r')

# 子图2(拟合的较好)
fig2 = fig.add_subplot(312)
plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2)
plt.plot(xSort[:,1],yhat2[srt],color='r')

# 子图3(过拟合)
fig3 = fig.add_subplot(313)
plt.scatter(xMat[:,1].A,yMat.A,c='b',s=2)
plt.plot(xSort[:,1],yhat3[srt],color='r')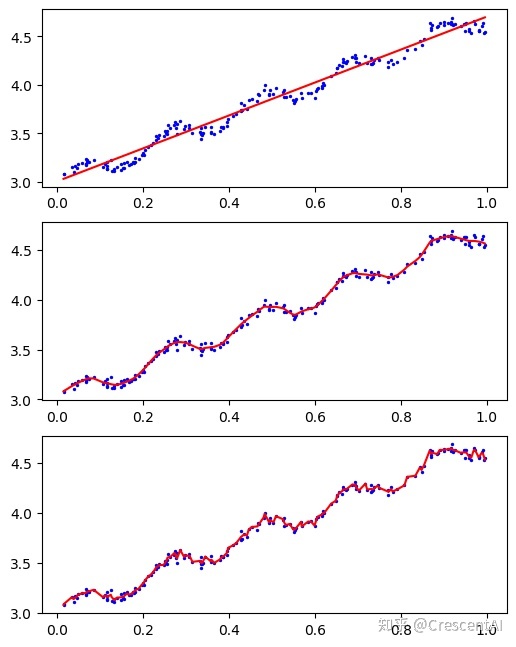

参考

吴恩达 CS229课程

周志华《机器学习》

李航《统计学习方法》

访问验证-安居客 ws:2019298239 机器学习-极大似然估计深入理解机器学习中的：目标函数，损失函数和代价函数_人工智能_qq_28448117的博客-CSDN博客 API详解:sklearn.linear_model.LinearRegression_人工智能_Sehr Gut-CSDN博客

私の未来は夢じゃない

关注

3
点赞
踩
10

收藏

觉得还不错? 一键收藏
0
评论
机器学习算法-线性回归

线性回归的概念1、线性回归的原理 2、线性回归损失函数、代价函数、目标函数 3、优化方法(梯度下降法、牛顿法、拟牛顿法等) 4、线性回归的评估指标 5、sklearn参数详解一、回归回归是一种预测建模技术，其中被估计的目标变量是连续的。回归应用的例子包括使用其他经济学指标预测股市指数，基于高空气特征流预测一个地区的降水量，根据广告开销预测公司的总销售，按照有机物质中的碳14残留...
复制链接

扫一扫