【步态识别】GaitGL 算法学习《Gait Recognition via Effective Global-Local Feature Representation and Local Temp》

1. 论文&代码源

《Gait Recognition via Effective Global-Local Feature Representation and Local Temporal Aggregation》
论文地址：https://ieeexplore.ieee.org/document/9710710
代码下载地址： 作者未提供

2. 论文亮点

1. 建立全局和局部特征提取器（GLFE）：

在特征提取过程中建立全局和局部特征提取器（Global and Local Feature Extractor, GLFE）；

2. 集成多个全局和局部卷积层（GLConv）：

GLFE中集成了多个全局和局部卷积层，全局卷积用于提取整个步态视觉外观的特征，局部卷积层用于提取步态细节（以principle方式提取特征）；

3. 构建局部时间聚合模块（LTA）：
为避免2D CNN空间池化降低分辨率导致信息丢失，为了更充分地利用空间信息，构建局部时间聚合模块（Local Temporal Aggregation, LTA），通过代替传统的空间池化层，聚合局部片段的时间信息，利用时间分辨率以获得更高的空间分辨率。

3. 模型结构

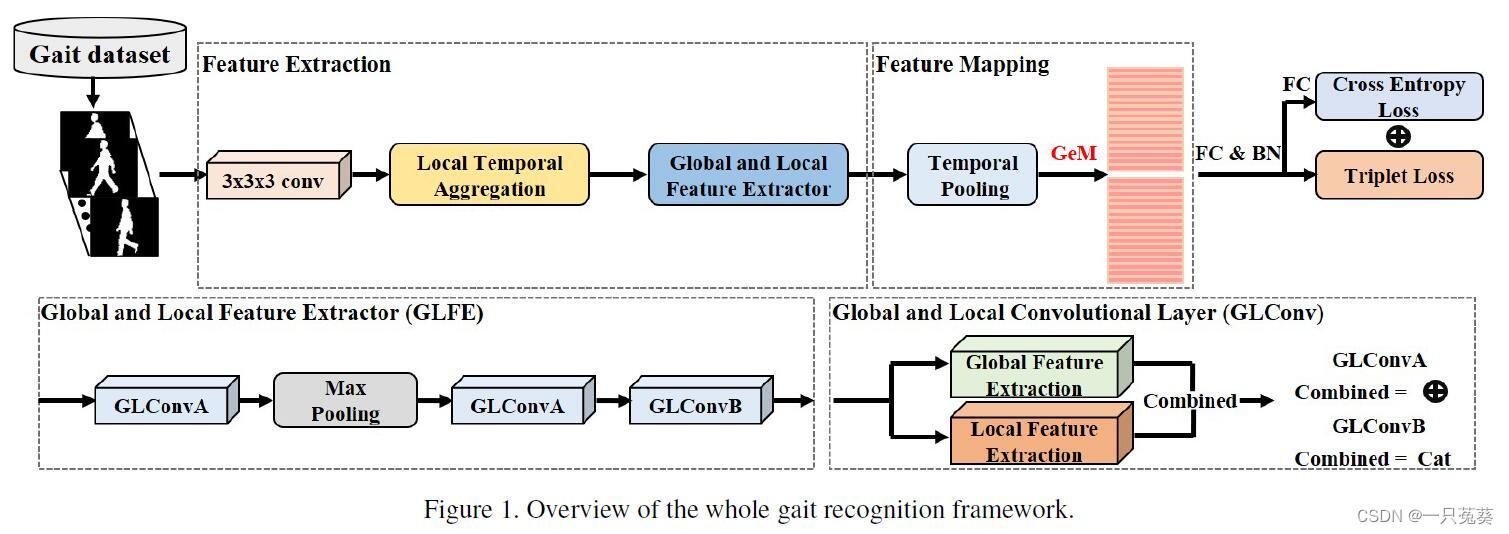
模型的结构如下图所示，目的是为了步态识别提取更全面的特征表示，大致分为3个关键部分。

首先使用卷积从原始输入序列中提取浅层特征，使用局部时间聚合操作（LTA）来聚合时间信息，以保留更多的空间信息；之后使用全局和局部特征提取器（GLFE），以提取全局和局部信息的组合特征；最后使用时间池化和GeM池化层来实现特征映射，并使用三元组损失和交叉熵损失来训练模型。

3.1 局部时间聚合（Local Temporal Aggregation, LTA）

LTA可以整合局部片段的时间信息，同时保留更多的空间信息。

假设$X_{in}\in {\mathbb{R}}^{C_1\times T_1\times H_1\times W_1}$是LTA的输入，其中，$C_1$是通道数；$T_1$是步态序列长度；$(H_1,W_1)$是每帧（步态）图像的大小，此模块的计算式为：$$X_{LTA}=f_{a\times a\times a}^{b\times 1\times 1}(X_{in})$$
$f_{a\times a\times a}^{b\times 1\times 1}(\cdot )$表示的是核大小为$a$，时间步长为$b$的3D CNN。

输出为$X_{LTA}\in {\mathbb{R}}^{C_2\times T_2\times H_1\times W_1}$

3.2 全局和局部特征提取（Global and Local Feature Extractor, GLFE）

尽管现有方法能够提取出局部特征，提供比步态特征更加详细的信息，但局部特征并没有注意到局部区域之间的关系，因此，作者提出了GLFE模块来同时利用全局和局部信息。

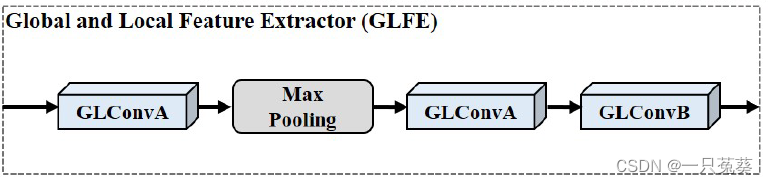
GLFE模块由GLConv层实现，它包含全局和局部特征提取器。根据组合的形式又可以分为GLConvA和GLConvB两种类型。

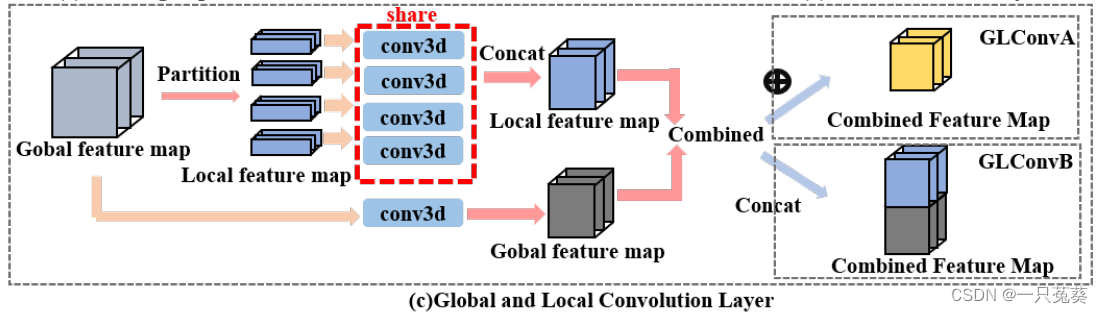
假设$X_{global}\in {\mathbb{R}}^{c_1\times t\times h\times w}$是LTA的输入，其中，$c_1$是通道数；$t$是特征序列长度；$(h,w)$是每帧（特征）图像的大小。

根据输入的下标$global$不难理解输入的是一张完整的特征图像，也就是全局图，现在需要将它分割为局部特征图，我们定义 X l o c a l = { X l o c a l i ∣ i = 1 , 2 , . . . , n } X_{local} = \{X_{local}^i | i=1,2, ..., n\} Xlocal​={Xlocali​∣i=1,2,...,n}，$n$是在图像高度上划分的区域数，划分得到$X_{locall}^i\in {\mathbb{R}}^{c_1\times t\times \frac{h}{n}\times w}$。

使用3D CNN分别提取全局和局部特征。
注意：提取局部步态的卷积网络权值共享

对全局和局部特征有两种结合方式：
$$\{\begin{array}{l}\text{逐元素加法 (GLConvA)}\\ \text{串联法 (GLConvB)}\end{array}$$
相应的表达式如下：
$$Y_{GLConvA}=Y_{global}+Y_{local}\in {\mathbb{R}}^{c_2\times t\times h\times w}$$$$Y_{GLConvA}=cat\left\{\begin{array}{c}{Y}_{global}\\ Y_{local}\end{array}\right\}\in {\mathbb{R}}^{c_2\times t\times 2h\times w}$$
其中，$Y_{global}$和$Y_{local}$的计算式分别为：
$$Y_{global}=f_{3\times 3\times 3}(X_{global})\in {\mathbb{R}}^{c_2\times t\times h\times w}$$$$Y_{local}=cat\left\{\begin{array}{c}{f}_{3\times 3\times 3}^{\prime }(Y_{local}^1)\\ f_{3\times 3\times 3}^{\prime }(Y_{local}^2)\\ ⋮\\ f_{3\times 3\times 3}^{\prime }(Y_{local}^n)\end{array}\right\}\in {\mathbb{R}}^{c_2\times t\times h\times w}$$
这里的$Y_{local}^i$和上文的$X_{local}^i$应该是一回事，只不过作者忘记改过来了？

GLFE中前几个用GLConvA，最后一个用GLConvB

3.3 特征图（Feature Mapping）

3.3.1 时间池化（Temporal Pooling, TP）

由于输入的步态序列长度可能不同，作者引入时间池化来聚合整个序列的时间信息，假设GLFE模块的输出为$X_{GLFE}\in {\mathbb{R}}^{C_3\times T_2\times H_2\times W_2}$，其中$C_3$通道数；$T_2$是特征图的长度；$(H_2,W_2)$是特征图的大小。

因为在GLFE中经历了空间维度上的池化，所以特征图的大小由$(h,w)$变为$(H_2,W_2)$。

时间池化$TP(\cdot )$可以用下式表示：
$$Y_{TP}=F_{Max}^{T_2\times 1\times 1}(X_{GLFE})$$其中$F_{Max}^{T_2\times 1\times 1}(\cdot )$为最大池化层；输出$Y_{TP}\in {\mathbb{R}}^{C_3\times 1\times H_2\times W_2}$。

3.3.2 广义平均池化（Generalized-Mean pooling, GeM）

为了提高特征表示能力，在时间池化后，步态特征图被分割成条状，并使用最大和平均两个统计函数来汇总每个条状的信息，空间特征映射可以表示为：
$$Y_{MA}=\alpha F_{Max}^{1\times 1\times W_2}(Y_{TP})+\beta F_{Avg}^{1\times 1\times W_2}(Y_{TP})$$输出$Y_{MA}\in {\mathbb{R}}^{C_3\times 1\times H_2\times 1}$，权重系数$\alpha$和$\beta$是预先设定好的，所以引出广义平均池化。

广义平均池化能够自适应地整合空间信息，其表达式为：
$$Y_{GeM}=(F_{Avg}^{1\times 1\times W_2}((Y_{TP}{)}^p){)}^{\frac{1}{p}}$$输出$Y_{GeM}\in {\mathbb{R}}^{C_3\times 1\times H_2\times 1}$，参数$p$是一个可以通过网络训练得到的学习参数，有一下两种情况：
$$\{\begin{array}{l}\text{if}p=1,Y_{GeM}={\text{Avg}}^{1\times 1\times W_2}(Y_{TP})\\ \text{if}p\to \infty ,Y_{GeM}={\text{Max}}^{1\times 1\times W_2}(Y_{TP})\end{array}$$

3.3.3 全连接（Fully Connection, FC）

引入多个独立全连接来聚合$Y_{GeM}$的通道信息，表达式为：$$Y_{out}=F_{sfc}(Y_{GeM})\in {\mathbb{R}}^{C_4\times 1\times H_2\times 1}$$

3.4 损失函数（Loss Function）

采用三元组损失和交叉熵损失：
$$L_{combined}=L_{tri}+L_{ces}$$$$L_{tri}=[D(F(i),F(k))-D(F(i),F(j))+m{]}_{+}$$

4. 模型的训练和测试

训练阶段：
与Giatset、GaitPart模型的参数设置类似，此处不一一赘述。
考虑到内存的限制，作者将输入序列的长度设定为一个固定值。

测试阶段：
为了计算Rank-1准确率，测试数据集被分为gallery set和probe set两组，gallery set被视为要检索的标准视图，而probe set的特征向量则用于匹配gallery中的特征向量。gallery与probe之间的度量策略可以使用欧氏距离、余弦距离等，本文使用的是欧氏距离。

5.实验结果

5.1 参数设置

实验使用的是CASIA-B和OU-MVLP两个数据集，具体的参数设置见下表：

5.2 模型准确率

5.2.1 CASIA-B

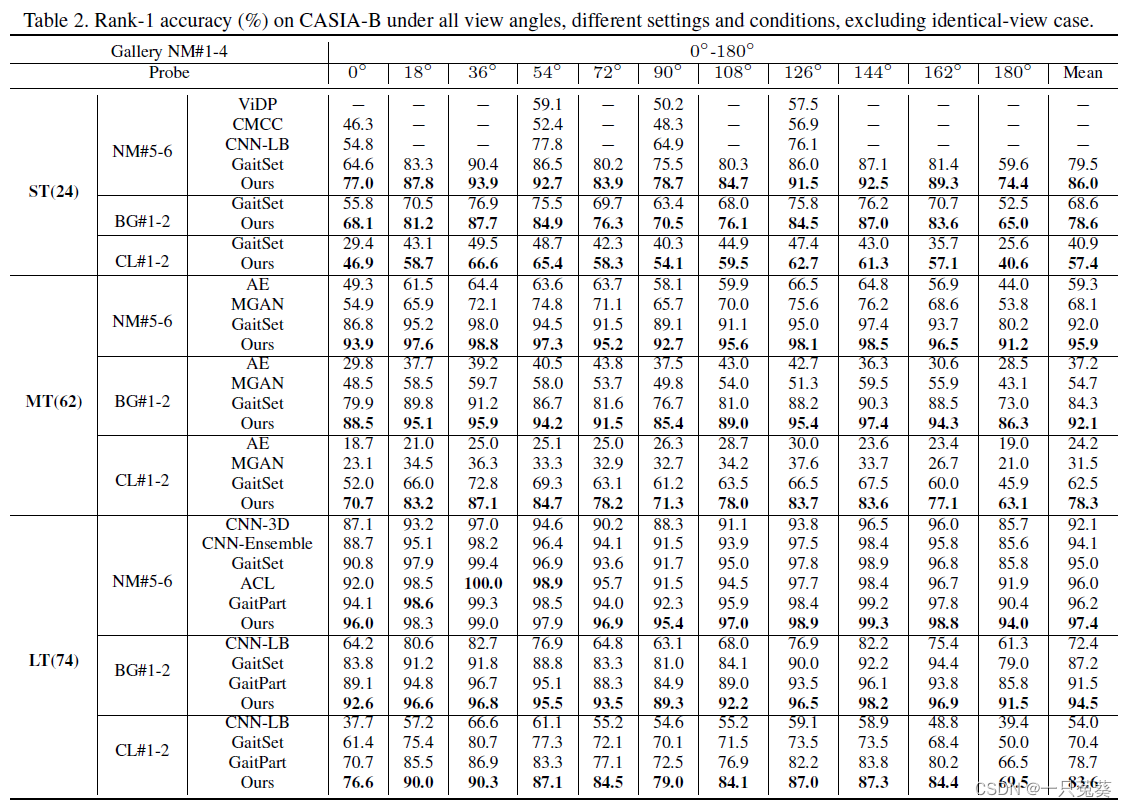
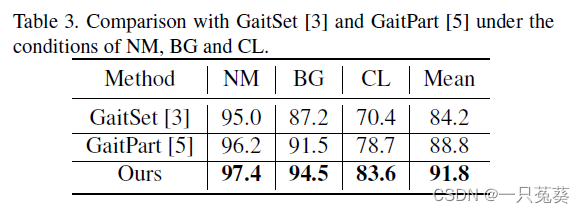
5.2.2 OU-MVLP

5.3 消融实验

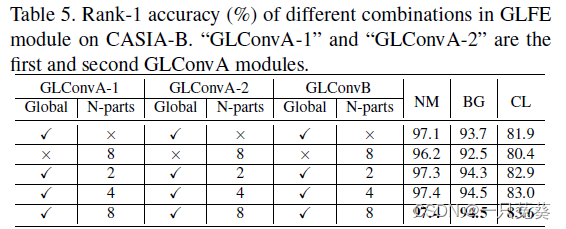
6.总结

本文提出了一个新的步态识别框架，基于三维卷积产生具有判别力的特征表示。
首先，为了提取更全面的步态信息，作者提出了一个全局和局部特征提取器（GLFE）来提取稳定的步态特征。其次，为了利用更多的信息，作者引入了局部时间聚合模块（LTA）来取代传统的空间聚合模块。此外，作者还引入了广义均值池化层（GeM）来自适应地聚合空间信息，提高特征映射的性能。
在公共数据集上的实验结果验证了识别框架的有效性。

参考博客：

（ICCV-2021）通过有效的全局-局部特征表示和局部时间聚合进行步态识别（一）

（ICCV-2021）通过有效的全局-局部特征表示和局部时间聚合进行步态识别（二）

（ICCV-2021）通过有效的全局-局部特征表示和局部时间聚合进行步态识别（三）