线性回归模型

最小二乘法与最小绝对偏差

最小二乘法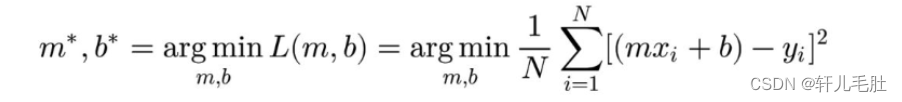： 最小绝对偏差：

在进行线性回归时，有这样一个想法，为什么不用这样的直线，它使得每个点到直线的 距离 之和最小？
这个 距离 (点与直线在 y轴 上的距离)之和叫做 least absolute deviation，也有人叫它 最小一乘法:

那我们为什么不用点到直线的 垂直距离 来作为我们的最小距离呢？

在许多任务中，如果样本的特征数超过样本数，导致X的列数多于行数，进而造成不满秩，此时可以得出多个解，它们都能使均方误差最小化。常见的做法就是引入正则化项。

L1范数: 通过稀疏化（减少参数数量）来降低模型的复杂度，即可以将参数值减小到0

L2范数: 通过减少参数值大小来降低模型复杂，即只能将参数值不断减小但永远不会减小到0

套索回归 （lasso regression）

与岭回归类似，套索 (Least Absolute Shrinkage and Selection Operator) 也会对回归系数的绝对值添加一个罚值。此外，它能降低偏差并提高线性回归模型的精度。看看下面的等式：
套索回归与岭回归有一点不同，它在惩罚部分使用的是绝对值，而不是平方值。这导致惩罚（即用以约束估计的绝对值之和）值使一些参数估计结果等于零。使用的惩罚值越大，估计值会越趋近于零。这将导致我们要从给定的n个变量之外选择变量。
要点：
• 除常数项以外，这种回归的假设与最小二乘回归类似；
• 它将收缩系数缩减至零（等于零），这确实有助于特征选择；
• 这是一个正则化方法，使用的是 L1 正则化；
• 如果一组预测因子是高度相关的，套索回归会选出其中一个因子并且将其它因子收缩为零。

岭回归（ridge regression） 

 岭回归存在的目的：

解决多重共线性下，最小二乘估计失效的问题

岭回归的作用：(在引入变量太多，又存在多重共线性，难以抉择去留哪个变量时可以通过该方法筛选变量)

1.找出多重共线性的变量，并提剔除部分

2.找出作用不大的变量

3.找出岭回归系数不稳定的变量

弹性网络回归（elastic net regression） 

图示lasso和Ridge的差异 

以二维数据空间为例说明lasso和Ridge的差异，如上图所示，两个图是对应于两种方法的等高线与约束域。

红色的椭圆代表的是随着λ的变化所得到的残差平方和， 为椭圆的中心点，为对应普通线性模型的最小二乘估计。

左右两个图的区别在于约束域，即对应的蓝色区域。 等高线和约束域的切点就是目标函数的最优解，Ridge方法对应的约束域是圆，其切点只会存在于圆周上，不会与坐标轴相切，则在任一维度上的取值都不为0，因此没有稀疏；对于Lasso方法,其约束域是正方形，会存在与坐标轴的切点，使得部分维度特征权重为0，因此很容易产生稀疏的结果。

所以，Lasso方法可以达到变量选择的效果，将不显著的变量系数压缩至0，而Ridge方法虽然也对原本的系数进行了一定程度的压缩，但是任一系数都不会压缩至0。
在实践中，在两个模型中一般首选岭回归。但如果特征很多，你认为只有其中几个是重要 的，那么选择 Lasso 可能更好。同样，如果你想要一个容易解释的模型，Lasso 可以给出 更容易理解的模型，因为它只选择了一部分输入特征。

线性回归

①它是一种监督学习算法，需要一组训练样本

②每个训练样本有一个或多个输入值和一个输出值

③该算法最适合训练样本的直线，平面或超平面

④使用学到的直线，平面或超平面来预测任何输入样本的输出值

⑤因线性模型简单易懂，且容易训练，通常优先被用来拟合新的数据集

⑥线性回归可以作为评估其他更复杂的回归模型的基线

算法优缺点
　　优点：

　　　　（1）思想简单，实现容易。建模迅速，对于小数据量、简单的关系很有效；

　　　　（2）是许多强大的非线性模型的基础。

　　　　（3）线性回归模型十分容易理解，结果具有很好的可解释性，有利于决策分析。

　　　　（4）蕴含机器学习中的很多重要思想。

　　　　（5）能解决回归问题。

　　缺点：

　　　　（1）对于非线性数据或者数据特征间具有相关性多项式回归难以建模.

　　　　（2）难以很好地表达高度复杂的数据。