Falcon Chapter 3

第三章猎鹰规范

3.1概述

        Falcon的主要元素是具有整数系数的n次多项式。次数n通常是2的幂(通常是512或1024)。计算是以n次一次多项式φ(其形式总是φ=+1)为模进行的。

        在数学上，在该算法中，一些多项式被解释为向量，而另一些则被解释为矩阵：多项式 f 模 φ 代表平方 n×n 矩阵，其行是所有 i 从 0 到 n-1 的  f mod φ ，证明了这种矩阵的加法和乘法映射为模φ多项式的加法和乘法。因此，我们可以用多项式上的运算来表示Falcon的大部分，即使我们真正处理的是定义格子的矩阵。

        公钥是维度为2n的格子的基础：

        

        这里的  是一个n维的单位矩阵，是只包含0，h是表示n×n子矩阵的多项式模φ，如上所述。h的系数是从0到q-1的整数，其中q是特定的小素数（q=12289）

        对应的私钥是完全相同的晶格的另一个基础，表示为：

 

        其中f、g、F和G是模φ的短整多项式，它们满足以下两个关系：

         这样的格被称为一个完整的 NTRU 格，第二个关系，特别是称为 NTRU 方程。请注意，当关系h=g/f表示为模q时，格子本身和多项式使用名义上的无界整数。

         密钥对生成涉及使用适当的分布选择随机f和g多项式，该分布产生较短但不太短的矢量；然后，求解NTRU方程以找到匹配的F和G。密钥在第3.4节中描述，其生成在第3.8节中介绍。

        签名生成包括首先将消息散列到符号，以及随机随机数，转换为多项式 c 模 φ，其系数统一映射到 0 到 q − 1 范围内的整数；这个过程在第 3.7 节中描述。然后，签名者使用他对秘密格基础（f，g，F，G）的知识来生成一对短多项式（s1，s2），使得 s1 = c - s2h mod φ mod q。正确说的签名是 s2。

        在通用性上，找到小向量 s1 和 s2 是一个昂贵的过程。Falcon 利用 φ 的特殊结构将其实现为类似于快速傅里叶变换的分而治之算法，大大加快了操作速度。此外，在采样向量中添加了一些“噪声”，具有仔细调整的高斯分布，以防止签名泄露太多关于私钥的信息。签名生成过程在第 3.9 节中描述。

        签名验证包括从散列消息 c 和签名 s2 重新计算 s1，然后验证 (s1, s2) 是一个适当的短向量。签名验证可以完全用模q的整数计算来完成;在第3.10节中描述。

        密钥和签名的编码格式在第3.11节中描述。特别是，由于签名是一个短多项式s2，其元素平均接近0，这允许自定义压缩格式减少签名大小。第 3.13 节定义了几个安全级别的推荐参数。

3.2技术概述

        在本节中，我们将概述所使用的技术。由于猎鹰可以说是数学密集型的，对数学原理的清晰理解对理解和实施它有很大的帮助。

        Falcon 使用 Q[x]/(φ) 形式的数字字段中的元素，φ = + 1 ，n =  我们注意到φ是一个循环多项式，因此它可以写成这个样子：φ(x) =∏k∈Z×m (x − ζk)，M=2n且ζ为1的任意本原m次根(e.g. ζ = exp( 2iπ/m )).

        关于这些数域Q[x]/（φ）的有趣之处在于，它们具有场塔结构。事实上，我们有以下领域：

         我们将依赖这个塔场结构。更重要的是，出于我们的目的，通过在奇数和偶数系数之间拆分多项式，我们有以下空间同构链：

        (3.4) 和 (3.5) 在用 Z 替换 Q 时仍然有效，在这种情况下，它们描述了一塔环和一个模块同构链。

        我们将在3.6节中看到，对于适当定义的乘法，这些实际上是环同构链。(3.5)将被用来使我们的签名生成更快、更好：在基于格的密码学中，签名的范数越小越好。因此，我们所说的“好”是指我们的签名生成将以较小的范数输出签名。一方面，域Q[x]/(xn+1)上的经典代数运算是快速的，使用它们将使我们的签名生成更快。另一方面，我们将使用(3.5)中暴露的同构作为杠杆来输出具有小范数的签名。利用这些自同态的全部潜力，需要处理多项式(或其傅立叶变换)的各个系数，并使用二叉树。

3.3 注解（一些数学公式和数学概念的解释）

        加密参数。对于密码签名方案，λ表示其安全级别，Qs表示签名查询的最大数量。在[NIS16]之后，我们假设Qs=。

        矩阵、向量和标量。矩阵通常为大写粗体(例如B)，向量通常为小写粗体(例如v)，标量(包括多项式)通常为斜体(例如s)。我们对向量使用行约定。矩阵B的转置可以表示为。应当注意的是，对于多项式f，在本文中我们不使用f‘来表示其导数。

        商环。对于Q∈N*，我们用Zq表示商环Z/qZ。在Falcon中，我们的整数模q=12289是素数，所以Zq也是一个有限域。由于q是一个素数，我们用表示Zq的可逆元群，使用欧拉函数φ(q) == q − 1 = 3 ·

        数字字段。Falcon使用多项式模数φ=+1(对于n=)。它是Z[x]的一元多项式，在Q[x]中不可约，在C上有不同的根。

         设a =  ，b = 是Q = Q[x]/(φ)域中的，我们注意到a⋆，并将a的（Hermitian）伴随称为Q的唯一元素，a*(ζ) = a(ζ)，其中·是C上通常的复杂共轭，对于 φ=+1，Hermitian 伴随 a*可以简单地表示：

         我们将此定义扩展到向量和矩阵：矩阵 B ∈ Qn×m 的伴随 B⋆（resp.向量v)是B转置的分量伴随(resp。v)：

       内积。Q上的内积〈·，·〉及其相关范数∥·∥是 ：        我们将这些定义扩展到向量：  对于我们选择的φ，内积与通常的系数式内积重合：       

        从算法的角度来看，计算内积或范数最容易的方法是：如果多项式采用FFT表示，则使用(3.8)；如果多项式采用系数表示，则使用(3.10)。

        环格。对于环 Q = Q[x]/(φ) 和 Z = Z[x]/(φ)，正整数 m ≥ n 和一个满秩矩阵 B ∈ Qn×m，我们用 Λ(B) 表示，并将B生成的晶格称为集合Zn，B = {zB|z ∈ Zn}。通过扩展，如果存在矩阵 B 使得 Λ = Λ(B)，则集合 Λ 是一个格。如果 q ⊆ Λ，我们可以说Λ ⊆  是一个 q 元格。

        离散高斯。整数上的离散高斯分布DZ，σ，μ为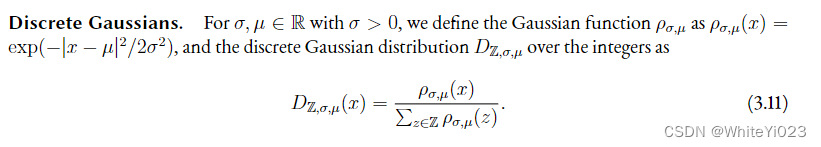

        Gram-Schmidt 正交化。任何矩阵 B ∈ Qn×m 可以分解为：

 其中L是下三角形，1在对角线上，当B为满秩时，这种分解是唯一的，称为Gram-Schmidt正交化（或GSO），我们还将B的Gram-Schmidt范数称为以下值：

        LDL ⋆ 分解。LDL⋆分解将任何满秩Gram矩阵写为乘积LDL⋇，其中L∈Qn×n是下三角形，对角线上有1，D∈Qn×n是对角线。LDL⋆分解和GSO密切相关，因为对于基B，存在唯一的GSO  B=L·B’，而对于全秩Gram矩阵G，存在唯一LDL⋅分解G=LDL⋇。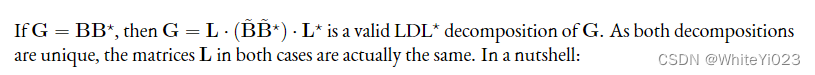，由于这两种分解都是唯一的，因此两种情况下的矩阵 L 实际上是相同的。简而言之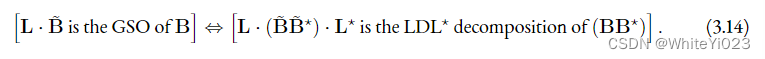：        我们呈现两种等效分解的原因是因为 GSO 是基于格的密码学中更熟悉的概念，而 LDL ⋆ 分解的使用更快，因此从算法的角度来看更有意义。