MHF-Net：用于多光谱和高光谱图像融合的可解释深度网络

一、摘要

摘要：多光谱和高光谱图像融合（MS/HS fusion）旨在融合高分辨率多光谱（HrMS）和低分辨率高光谱（LrHS）图像以生成高分辨率高光谱（HrHS）图像，这已成为高光谱图像处理最常见问题之一。在本文中，我们专门为MS/HS融合任务设计了一种网络架构，称为MHF-net，它不仅具有清晰的可解释性，而且也合理地嵌入了学习良好的连接HrHS图像到HrMS和LrHS图像的线性映射关系。特别地，我们首先构建了一个 MS/HS 融合模型，将低分辨率图像的泛化模型和 HrHS 图像的低秩先验知识合并为一个简洁的公式，然后我们通过展开近端梯度算法来构建所提出的网络用于解决所提出的模型。由于模型和算法的精心设计，MHF-net中的所有基本模块都具有明确的物理意义，因此易于解释。这不仅极大地方便了人们对网络内部发生的情况进行简单直观的观察和分析，而且具有良好的泛化能力。基于MHF-net的架构，我们进一步针对实践中的两种常见情况设计了两种深度学习机制：一致性MHF-net和盲目MHF-net。前者适用于训练数据和测试数据的光谱和空间响应一致的情况，正如大多数以往的一般监督 MS/HS 融合研究所考虑的那样。后者确保了训练和测试数据中光谱和空间响应不匹配情况下的良好泛化，甚至跨不同传感器，这通常被认为是一般监督 MS/HS 融合方法的一个具有挑战性的问题。模拟和真实数据的实验结果在视觉和定量上证实了我们的方法与该研究领域最先进的方法相比的优越性。

二、结论

在本文中，我们建立了一种新的可解释的专为MS/HS融合任务设计的网络体系结构，称为MHF-net。与目前大多数网络结构相比，它的特点是所有的基本模块构成网络都有自己的物理意义，包括$\chi$的重建，LrHS残差$\epsilon$，底层HrMS谱基础$\hat{y}$及其改善梯度方向$\mathcal{G}$。这使得在训练（和测试）网络的过程可以非常方便观察和理解网络流。此外，在网络中嵌入了内在的泛化机制，保证了如何从HrHS中获得LrHS/HrMS的观测模型，便于我们很好地得到底层传感器的泛化原理。另外，一般的HrHS所拥有的光谱低秩先验在网络中被明确地传递，保证了在网络的输出和中间阶段的恢复$X$能够在一个良好的先验结构中被正则化，并自然地提高了恢复的HrHS的精度。

此外，与目前大多数的深度学习方法都存在训练样本的过拟合问题相比，该网络可以很容易地实现对不同光谱和空间响应函数下的训练样本的处理，从而能够捕捉到响应变化下的不变重建规律。这使得它能够很好地推广到测试图像，即使它们的波段数、强度和光谱响与训练图像都不同。在一系列合成和真实数据上进行的实验证明，与传统的基于模型的SOTA方法和更流行的基于深度学习的SOTA方法相比，所提出的网络在综合$PQ{I}_s$方面具有优势。

全分辨率质量仍然是一个悬而未决的问题。事实上，仍有很大的空间来进一步提高性能。首先，(22)中的近端网络可以设计得更好(在我们的工作中很容易设置为ResNet)，对性能有一定的影响。此外，我们很容易使用二次损失来构建训练损失，而特定任务的损失也可以进一步提高性能。此外，与以往的大多数方法一样，该模型使用线性映射将HRHs图像与LRMS和HRMS图像关联起来。

然而，在实际情况下，由于对HRMS和LRMS图像进行强度对准和其他操作，这种关系总是非线性的。通过以下方法，MHF-Net将可能清晰表达这种非线性关系。
1)用更复杂的非线性下采样子网络代替线性下采样子网络，得到高分辨率图像和低分辨率图像之间的非线性关系。
2)在前级HrHS输出与最终输出之间的线性映射之间嵌入更复杂的网络而不是简单的ResNet，以捕捉它们之间更复杂的非线性关系。
3)在输入的HrMS和LrHS图像之后直接插入网络映射，得到转换后的映射，用于连接后续网络，传递三种类型HIS之间的潜在非线性关系。

我们将在未来的研究中尝试这些策略。

三、背景介绍introduce

高光谱(HS)成像获取各种连续光谱波段的场景。与具有一个或几个波段的传统图像(例如，具有RGB通道的彩色图像)相比，HS图像提供了更精细的真实场景知识的传递。这倾向于有利于成像场景的表征，并提高不同计算机视觉任务的性能，例如对象识别、分类和分割[13]、[40]、[41]。此外，HS图像丰富的光谱也促进了相关应用的新范围，如目标检测[26]和光谱分解[4]。

然而，在实际情况下，HS成像系统的空间分辨率和光谱分辨率之间不可避免地存在权衡。具体地说，精细记录具有大量光谱波段的图像不仅需要更多的曝光次数，而且需要更长的曝光时间。通常，光学系统只能提供高空间分辨率但低光谱分辨率的数据(例如，标准RGB图像)，反之亦然。

因此，如何将实际采集到的高分辨率多光谱(HRMS)图像与低分辨率高光谱(LrHS)图像融合以生成理想的高分辨率高光谱(HRHs)图像，即多光谱/高光谱(MS/HS)融合，近年来引起了人们的极大关注[53]。

观测到的HRMS和LrHS图像是如何从其原始HRHs图像生成的，其机理可以用以下两个线性观察模型(如图1所示，以便于理解)[4]、[15]、[17]、[29]、[45]、[46]进行数学描述：

其中$X\in {\mathbb{R}}^{HW\times S}$代表目标HrHS 影像，${}^1$$H,W$ 和$S$ 分别代表它的高、宽和波段数。 $Y\in$ ${\mathbb{R}}^{HW\times s}$ 代表 HrMS 影像， $s$ 代表其波段数 $(s\ll S)$, 和$Z\in {\mathbb{R}}^{hw\times S}$ 代表LrHS 图像，其中$h$ 和$w$ 分别代表它的高和宽 $(h\ll H,w\ll W)$。 $R\in {\mathbb{R}}^{S\times s}$ 代表 HrMS 图像的光谱响应矩阵 (如 图. 1a所示). $C\in {\mathbb{R}}^{hw\times HW}$ LrHS 图像的空间退化矩阵, 它通常被假设由循环卷积算子 $\mathbf{\varphi }$ 和区间固定下采样算子D组成(如图1B所示)。 $N_y$ 和$N_z$ 分别是HRMS和LrHS图像中包含的噪声。这两个观察模型在以前的许多MS/HS融合研究中得到了广泛的利用[4]，[29]，[45]。

1.HS图像也可以写成张量$\mathcal{X}\in {\mathbb{R}}^{H\times W\times S}$。我们还把从矩阵到张量的重塑算子表示为：折叠式$\text{ fold }(X)=\mathcal{X}$

MS/HS融合问题可以被解释为从两个退化的数据立方体恢复三维数据立方体的反问题，而困难主要在以下两个方面。首先，从退化的HRMS图像Y和LrHS图像Z直接获取具有观测模型(1)和(2)的HRHs图像X是一个病态的逆问题，即使在R和C已知的情况下也是如此。这导致需要在传统的无监督方法中将X的先验结构以数学方式编码到正则化器中，然而，这是一项相当具有挑战性的任务。其次，不同传感器获取的数据的光谱和空间响应R和C可能差异很大，这大大增加了用监督方法求解这一问题的难度。

具体而言，在传统的无监督MS/HS融合方法中，通常需要在X上预先假定一个先验作为正则化器来求解问题。例如，早期的MS/HS融合技术继承了泛锐化原理，用小波级数展开[14]表示HS图像，[61]。然后，进一步利用HS图像上的先验空间稀疏表示，假设HS图像的空间信息可以在一个学习字典[2]，[15]，[63]下稀疏表示。[31]在HrHS图像上采用了局部空间平滑先验，并在模型中使用了总变差(TV)正则化。最近的一些方法不是从HrHS中探索空间先验知识，而是在HrHS上假设更多的内在频谱相关先验，并采用低秩矩阵分解技术沿频谱[30]，[54]编码这种先验，[62]。尽管对某些HS图像处理应用是有效的，但这些技术的合理性依赖于人工对待恢复的未知HrHS的预先假设。然而，这些具有主观和相对简单形式的手工先验总是不能充分和自适应地反映真实HSI内在复杂的空间和光谱结构。因此，这些方法的性能仍有改进的空间。

随着大多数计算机视觉任务的发展[6]、[39]、[56]，基于深度学习的有监督方法最近才进入HS/MS融合领域，并取得了比传统方法更具竞争力的性能[32]、[35]。与传统的无监督方法相比，这些基于数据挖掘的方法具有优势，因为它们需要更少的关于待恢复HRH的先验知识的假设，并且它们可以直接在一组成对的训练数据上训练，模拟网络的输入(LrHS和HRMS图像)和输出(HRHS图像)。最常用的网络结构包括CNN[9]、3DCNN[32]和残差网络[35]。网络输入通常通过将HRMS图像Y和LrHS一Z堆叠在一起来获得(Z通常被预先内插到与Y相同的空间大小)，并且使用随机梯度下降(SGD)或其他训练算法来更新所有网络参数。

目前基于深度学习的MS/HS融合方法虽然取得了较好的效果，但仍存在一定的缺陷。最关键的一点是，这些方法是在其他任务中常用的通用框架下提出的，但不是专门为MS/HS融合设计的。特别是，现有的动态学习方法忽略了观测模型(1)和(2)[32]、[35]，特别是算子R和C，这使得这些方法很难提供关于LrHS和HrM是如何由HRH产生的内在理解，并且失去了对网络设计中问题的特定解释性。此外，现有的深度学习方法在很大程度上忽略了一般HS图像明显具有的先验结构，如光谱低秩特性。这可能导致网络输出偏离初衷，从而影响重建的准确性。当前DL方法的另一个关键问题是其泛化能力。由于人工和硬件成本的限制，只能采集到有限数量的成对训练HS图像，实际案例中经常存在训练-测试偏差的不匹配问题。在这种情况下，当前的深层网络往往会出现过拟合问题。因此，设计一个能够很好地拟合测试样本的深度学习架构是可取的，即使它们的光谱和空间响应与训练样本不同。

针对上述问题，本研究探索了一种新的MS/HS融合任务深度网络架构，该架构具有比现有架构更好的可解释性和泛化能力${}^2$。本工作的贡献主要可以概括为以下几点:

2.作为我们会议文件[49]的扩展版本，这项工作取得了实质性的扩展，特别是在新网络的内在可解释性和泛化能力方面，包括更多的澄清、分析、方法扩展和实证评估。具体地说，针对训练数据和测试数据的响应系数不一致的情况，提出了一种扩展的网络，使该方法也适用于这种更实际的盲MS/HS融合场景。

第一，我们提出了一个超越传统的MS/HS融合优化问题。具体来说，常规使用的观测模型(1)并没有充分反映HrHS图像X的低秩先验结构，因为Y的列向量通常只构成X的不完全基集。相比之下，新的优化问题是在X的完全基集$[Y,\hat{Y}]$下表示（例如$X=YA+\hat{Y}B$，其中系数矩阵A和B需要在训练过程中进行估计${}^3$）。$\hat{Y}$由深度网络产生。为了便于理解，可以参见图2b。

3.通过这个$[A^T,B^T{]}^T$转置矩阵可以求得空间响应矩阵前s列的数值，6.1节由详细解释

这种新的方式不仅提供了更充分的表示模型，既保证了低秩度，又便于我们通过展开近端梯度算法来求解它，从而容易地构建一个可解释的网络结构[3]。

第二，展开的网络称为MS/HS融合网络或MHF-Net，具有良好的可解释性。据我们所知，这是第一个充分考虑MS/HS融合内在生成机制的DL方法。特别是，在MHF-Net中，所有模块都有其特定的物理含义，模块之间的所有连接恰好对应于算法的实现算子，从理论上保证了HRMS/LrHS生成的观测模型贯穿整个网络流。与传统的或多或少的黑匣子网络架构相比，MHF-net更容易直观地观察网络内部发生的事情，直观地分析和理解其实现机制。

第三，MHF-net在网络架构的每一阶段明确地将表现很好的光谱低秩先验和观测模型(1)的约束编码到待恢复的HrHS图像中(如图4所示)。在该网络表达式的正则化下，HrHS的恢复(无论是最终输出还是中间网络阶段获得的结果)都很好地符合其固有先验结构。因此，相对于之前没有明确考虑这种HrHS先验结构的深度学习方法，具有更好的可靠性和准确性。

第四，这种可解释网络具有良好的泛化能力。一方面，当训练数据和测试数据的光谱和空间响应一致时，所有响应参数(A、B和C)以及网络参数都可以端到端的方式从训练数据中自动学习。因此，该网络可以帮助提取观测模型，并被推广到模拟底层传感器的泛化过程。另一方面，对于更一般的场景，其中从不同的传感器设置或甚至不同的传感器获取具有不同光谱和/或空间响应的训练图像，我们可以将这些响应知识以及LrHS和HRMS图像输入网络，并训练网络使其能够捕获不同输入光谱和空间响应下的一般恢复原理。因此，训练的网络可以被很好地推广，以有效地用于测试具有不同响应的图像，甚至用于那些从训练数据中明显失配的图像。

这篇论文的组织方式如下。第二节回顾了相关的研究成果。第三节介绍了为该任务构建的新的观测模型，以及相应的优化问题及其求解算法。本部分还介绍了正在展开的网络体系结构。在此网络结构的基础上，第四节提出了适用于相似训练测试响应的一致性MHF-Net，第五节提出了失配训练测试响应下的盲MHF-Net。第六节给出了在一系列合成数据和真实数据上的实验结果，并与现有的SOTA算法进行了比较，从视觉和定量两个方面证明了该方法在综合量化度量方面的优越性。论文最后对下一步的工作进行了展望。在整篇文章中，我们分别用非粗体字母、粗体小写字母、粗体大写字母和书法大写字母表示标量、矢量、矩阵和张量。

四、相关工作

4.1传统的非监督方法

遥感中的全色锐化技术与所研究的MS/HS融合问题密切相关，其目的是通过MS图像和宽带全色图像的融合来获得高空间分辨率的MS图像。泛锐化方法主要有两类：成分替换(CS)[1]、[7]和多分辨率分析(MRA)[5]、[25]、[38]。虽然我们可以简单地将MS/HS融合处理为多个全色锐化的子问题，其中HRMS图像的每个波段都扮演着全色图像的角色，但这种启发式策略总是受到高光谱失真的影响，因为单一的全色图像包含的光谱信息太少，无法表达预期的HS图像。

在过去的几年里，基于模型的方法通过直接施加某些先验项来正则化待估计的HRHs图像[2]、[15]、[21]、[54]、[62]、[63]，从而在MS/HS融合问题上受到了广泛的关注。从自然图像借用的一些一般先验已经被容易地采用，一些从自然图像中借鉴来的一般先验很容易被采用，比如表示HS图像空间局部平滑度的TV术语[31]。此外，典型的一类方法是在HrMS图像的非局部块上学习空间字典，传递HrHS的空间知识，然后从LrHS中学习系数矩阵，用于表示和恢复HrHS[2]，[15]，[45]，[63]。另一种方法使用稀疏矩阵分解来学习LrHS图像的光谱字典，然后通过利用光谱字典和HRMS图像来构建HRHS图像[17]。还可以利用HS图像的光谱低秩性，使用矩阵/张量分解，这有助于减少光谱失真，提高MS/HS融合性能[21]，[30]，[54]，[62]。

这些方法的主要缺点是它们的有效性依赖于手动预先指定的施加在HrHS图像上的先验项，而大多数方法人工先验假设可能无法全面反映从实际场景中采集的真实HrHS图像的多样化和复杂配置。

4.2基于深度学习的监督方法

最近，利用不同的网络结构[22]、[23]、[27]、[33]、[34]、[35]、[37]、[47]，提出了许多基于深度学习的泛锐化方法。这些方法可以很容易地适应于MS/HS融合问题。例如，Masi等人[27]提出了一种泛锐化CNN，称为PNN，并取得了令人满意的效果。该网络的输入是全色图像和相应的MS/HS图像的拼接，这些图像事先被插值到与全色图像相同的空间大小。随后，Wei等[47]通过构建深度残差网络对PNN进行了改进。此外，Palsson等人[32]提出在与PNN相似的结构中使用3D-CNN。由于三维卷积在处理高维数据时的强大性能，与传统方法相比，结果非常有希望。

然而，这些基于dl的方法仍然有明显的缺点。例如，他们只是使用当前深度学习工具包中一些现成组件组装的网络，这些组件不是针对所研究的问题专门设计的，因此对该特定任务没有特定的可解释性。特别是，这种“黑箱”深度模型忽略了HS图像所具有的本征观测模型(1)/(2)，以及光谱相关等明显的先验结构，有很大的性能提升空间。此外，这些数据驱动的方法对光谱和空间响应的变化非常敏感，特别是训练数据和测试数据之间的不匹配。然而，这种过拟合问题应该是至关重要的，因为实际数据通常是在不同的传感器设置下甚至使用不同的传感器收集的，并且这种训练-测试偏差在实践中普遍存在。

4.3 深度展开方法 Deep Unrolling Methods

深度展开方法将传统的基于模型的方法与深度学习方法联系起来，深度学习方法通常通过将迭代优化算法展开为分层深度网络架构[10]，[43]，[50]，[51]，[59]，[64]来构建。这类方法已被广泛应用于各种计算机视觉任务中，包括压缩感知、去雾、反卷积等[50]，[51]，[64]，并被证实是有效的。我们的方法受到了这一研究路线的启发，并旨在为我们的研究任务构建一个深度展开的网络框架。然而，我们更期望的是深入研究这样一个有前途的方法，从而可能地探索和展示这种受模型启发的网络体系结构自然拥有的强大的解释和泛化能力。

五、 MS/HS融合模型

5.1模型公式

我们首先引入一个表示观测模型(1)的等价公式。具体来说，我们有以下定理。证明是在补充材料中提出的，在计算机学会数字图书馆http://doi.ieeecomputersociety.org/10.1109/ TKDE.2020.3015667上可以找到补充材料中的证明。

定理 1. 对于任何 $X\in {\mathbb{R}}^{HW\times S}$ 和$\tilde{Y}\in {\mathbb{R}}^{HW\times s}$, 如果$\mathrm{rank}(X)=r>s$ 和$\mathrm{rank}(\tilde{Y})=s$, 那么下面的两个表述是相互等价的：
(a) 存在$R\in {\mathbb{R}}^{S\times s}$, 使得等式（3）成立,
$$\tilde{Y}=XR\text{. }（3）$$
(b) 存在 $A\in {\mathbb{R}}^{s\times S},B\in {\mathbb{R}}^{(r-s)\times S}$ 和$\hat{Y}\in$ ${\mathbb{R}}^{HW\times (r-s)}$,等式（4）成立,
$$X=\tilde{Y}A+\hat{Y}B.（4）$$

在实际应用中，由于HrMS图像的光谱数通常比HrHS图像的光谱数少得多，因此光谱响应矩阵的列是线性独立的，因此通常满足$\mathrm{rank}(\tilde{Y})=s$ 条件，即HrMS图像在光谱模式上通常是全秩的。因此，令$\tilde{Y}=Y-N_y$ ，其中$Y$为观测模型(1)中的HrMS，很容易发现$\tilde{Y}$和X满足定理1中的条件。则观测模型(1)可重新表述为:
$$X=YA+\hat{Y}B+N_x,（5）$$
其中$N_x=-N_{y}A$ 是由 HrMS 图像中的噪声引起的。 注意，在（5）中， $[Y,\hat{Y}]\in {\mathbb{R}}^{HW\times r}$ 可以看做一个完整的基集，基的个数$r$ 表示 $X$ 中的列数，其系数矩阵$[A;B]\in {\mathbb{R}}^{r\times S}$, 只有基于 $\hat{Y}$的 $r-s$ 是未知的且需要被估计。

再考虑观测模型(2)，我们可以得出以下推论:

推论1. 对于任何的 $\tilde{Y}\in {\mathbb{R}}^{HW\times s},\tilde{Z}\in {\mathbb{R}}^{hw\times S},C\in {\mathbb{R}}^{hw\times HW}$，如果$\mathrm{rank}(\tilde{\mathbf{Y}})=s$ 和$\mathrm{rank}(\tilde{\mathbf{Z}})=r>s$, 那么下面的两个等式是等价的：
(a) 存在 $X\in {\mathbb{R}}^{HW\times S}$ 和$R\in {\mathbb{R}}^{S\times s}$, 满足,
$$\tilde{Y}=XR,\tilde{Z}=CX,\mathrm{rank}(X)=r.$$
(b) 存在 $A\in {\mathbb{R}}^{s\times S},r>s,B\in {\mathbb{R}}^{(r-s)\times S}$ 和$\hat{Y}\in$ ${\mathbb{R}}^{HW\times (r-s)}$,满足，
$$\tilde{Z}=C(\tilde{Y}A+\hat{Y}B).$$

让$\tilde{Z}=Z-N_z$, 其中$Z$ 是观测模型（2）中的LrHS 图像。容易发现，当被视为被估计的$X,R$ 和 $C$的方程时，观测模型（1）和观测模型（2）可以重新表示为$\hat{Y},A,B$ 和$C$ 的方程：
$$Z=C(YA+\hat{Y}B)+N$$
其中$N=N_z-C{N}_{y}A$ 表示HRMS和LrHS图像中包含的噪声。然后，我们可以直观地设计以下MS/HS融合的优化问题：

$$\underset{\hat{Y}}{\min }\Vert C(YA+\hat{Y}B)-Z{\Vert }_F^2+\lambda f(\hat{Y}),$$
其中$\lambda$是权重参数，$f(\cdot )$是施加在$\hat{Y}$上的正则化项。在传统的基于模型的方法中，一个核心问题是根据某些先验假设设计正则化函数[48]、[55]。然而，目前的研究表明，数据驱动的深度表征先验在其更充分和更自适应的先验拟合能力方面具有优势。因此，我们倾向于通过一个深入展开的网络来学习$f(\cdot )$对$\hat{Y}$的影响，而不是直接设计$f(\cdot )$。更多细节将在后面的章节中给出。

请注意，我们将正则化直接施加在待估计的基准$\hat{Y}$上，而不是像传统方法所做的那样将正则化施加在HrHS图像(X)上。该设置有助于完整地保存包含在输入HRMS图像(Y)中的空间细节，并有助于减少最终估计的HrHS图像(X)的空间细节损失，因为X的空间细节主要来自Y。

在这里，我们就响应参数给出以下必要的说明。当在相同的传感器设置(它们共享相同的光谱或空间响应)下获得所有训练HRMS和LrHS图像时，A、B和C是可以从整个训练数据适当地获得的固定矩阵。由此可以得到底层传感器的泛化机理。当在不同传感器设置下或从不同传感器获得数据集中的HRMS或LrHS图像时，每对HRMS和LrHS图像的A、B和C可以彼此不同。幸运的是，以前的方法已经表明，只需一对HRMS和LrHS图像就可以合理地估计光谱和空间响应(R和C)[45]。因此，还可以近似地提取该特定输入对的生成机制，并将其用于所提出的框架中。

5.2 模型优化

We now readily solve model (10) with a proximal gradient algorithm [3], which iteratively updates $\hat{Y}$ by calculating
$${\hat{\mathbf{Y}}}^{(k+1)}=\arg \underset{\hat{\mathbf{Y}}}{\min }Q\left(\hat{\mathbf{Y}},{\hat{\mathbf{Y}}}^{(k)}\right),$$
where ${\hat{Y}}^{(k)}$ is the updated variable in $k$ th iteration, and $Q\left(\hat{Y},{\hat{Y}}^{(k)}\right)$ is a quadratic approximation [3] defined as:
$$\begin{array}{rl}Q\left(\hat{Y},{\hat{\mathbf{Y}}}^{(k)}\right)=& g\left({\hat{\mathbf{Y}}}^{(k)}\right)+⟨\hat{\mathbf{Y}}-{\hat{\mathbf{Y}}}^{(k)},\nabla g\left({\hat{\mathbf{Y}}}^{(k)}\right)⟩\\ & +\frac{1}{2\eta }{\Vert \hat{\mathbf{Y}}-{\hat{\mathbf{Y}}}^{(k)}\Vert }_F^2+\lambda f(\hat{\mathbf{Y}}),\end{array}$$
where $g\left({\hat{Y}}^{(k)}\right)={\Vert C\left(YA+{\hat{Y}}^{(k)}B\right)-Z\Vert }_F^2$ and $\eta$ plays the role of stepsize.
It is easy to deduce that problem (10) is equivalent to:
$$\underset{\hat{Y}}{\min }\frac{1}{2}{\Vert \hat{Y}-\left({\hat{Y}}^{(k)}-\eta \nabla g\left({\hat{Y}}^{(k)}\right)\right)\Vert }_F^2+\lambda \eta f(\hat{Y}).$$

For many kinds of regularization terms, the solution of Eq. (12) is usually in closed-form written as [11]:
$${\hat{\mathbf{Y}}}^{(k+1)}={\mathrm{prox}}_{\lambda \eta }\left({\hat{\mathbf{Y}}}^{(k)}-\eta \nabla g\left({\hat{\mathbf{Y}}}^{(k)}\right)\right),$$
where ${\mathrm{prox}}_{\lambda \eta }(\cdot )$ denotes a proximal operator dependent on $f(\cdot )$. Since $\nabla g\left({\hat{Y}}^{(K)}\right)=C^T\left(C\left(YA+{\hat{Y}}^{(K)}B\right)-Z\right)B^T$, we can

deduce that the final updating rule for $\hat{Y}$ is

$${\hat{Y}}^{(k+1)}={\mathrm{prox}}_{\lambda \eta }\left({\hat{Y}}^{(k)}-\eta C^T\left(C\left(YA+{\hat{Y}}^{(k)}B\right)-Z\right)B^T\right).（14）$$
This concise iteration equation readily inspires an unfolding
network architecture by separating and transforming each of its involved operators as a specific form of network con- nection. Note that the implicit proximal operator can be eas- ily represented as a convolution network module and automatically learned from training data in an end-to-end manner, instead of being derived from the regularization term manually pre-specified.

5.3 MS/HS融合网络设计

3.3 MS/HS融合网络设计
然后，我们通过在更新等式（14）中展开所有算子作为网络层，为MS/HS融合构建可解释的深度网络架构。这种展开技术已被广泛用于各种计算机视觉任务，并已被证实是有效的[50]、[59]、[64]。该网络具有K个阶段，对应于求解方程（10）的迭代算法中的K次迭代。如图4a和4b所示。每一级将HrMS图像Y、LrHS图像Z和前一级$\hat{Y}$的输出作为输入，并输出更新的$\hat{Y}$作为下一层的输入。

算法展开。我们首先将更新方程（14）分成以下基本算子：
$$\begin{array}{rlrlrlrlrlr}{X}^{(k)}=YA+{\hat{Y}}^{(k)}B,& & & & & & & & & & (15)\\ E^{(k)}=C{X}^{(k)}-Z,& & & & & & & & & & \text{(16)}\\ G^{(k)}=\eta C^T{E}^{(k)}{B}^T,& & & & & & & & & & \text{(17)}\\ {\hat{Y}}^{(k+1)}={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\lambda \eta }({\hat{Y}}^{(k)}-G^{(k)}).& & & & & & & & & & \text{(18)}\end{array}$$

在网络框架中，我们使用图像及其张量格式( $\mathcal{X}\in {\mathbb{R}}^{H\times W\times S}$ ，$\mathcal{Y}\in {\mathbb{R}}^{H\times W\times s}$ ， $\mathcal{Z}\in {\mathbb{R}}^{h\times w\times S}$ )而不是矩阵形式以保护它们的空间结构，并使网络结构(具有张量形式)易于设计。因此，我们设计网络以张量格式执行上述操作，为了便于理解，如图3所示。

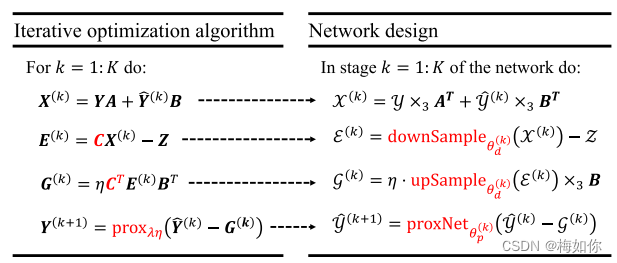
Fig. 3. An illustration of the relationship between the algorithm in matrix form and the network structure in the tensor form.