十大机器学习笔记持续更新,欢迎免费订阅专栏和关注!
一、有监督学习
有监督学习中,模型通过输入数据和对应标签进行训练,以学习预测正确输出。
1.1 标签(Label)
在有监督学习中,每个数据点都配有一个表示其真实结果或分类的标签。
- 对于分类问题,标签通常是类别的名称,例如在垃圾邮件检测中,标签可能是“垃圾邮件”或“非垃圾邮件”。
- 对于回归问题,标签是连续的数值,例如房价、气温或股票价格等。
二、机器学习概念
- Data:输入数据。
- Loss Function:损失函数,衡量模型预测值与实际值之间的差异。
分类与回归
- 分类:预测离散标签,如垃圾邮件检测。
- 回归:预测连续值,如房价预测。
三、线性回归
3.1 回归方程(拟合)
拟合是模型学习数据的过程,目的是最小化预测误差。
线性回归模型的一般形式为:
y
=
β
0
+
β
1
x
1
+
β
2
x
2
+
…
+
β
n
x
n
+
ϵ
y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n + \epsilon
y=β0+β1x1+β2x2+…+βnxn+ϵ
其中 (
y
y
y ) 是预测值,(
x
1
x_1
x1,
x
2
x_2
x2,
…
\ldots
…,
x
n
x_n
xn ) 是特征,(
β
0
\beta_0
β0,
β
1
\beta_1
β1,
…
\ldots
…,
β
n
\beta_n
βn ) 是模型参数,(
ϵ
\epsilon
ϵ ) 是误差项。
3.2 偏置和误差
- 误差 ϵ \epsilon ϵ:每一个样本对应着不同的误差,反应数据的不确定性和波动
- 偏置 θ:对应着样本的整体误差,反应模型和真实数据的偏差
- 截距项 β 0 \beta_0 β0:线性回归模型中,当所有特征值为零时的预测值。
误差公式:
每个样本的误差 (
ϵ
i
\epsilon_i
ϵi) 不同,
在线性回归中,对于每个样本的误差可以通过以下公式表示:
ϵ i = y i − y ^ i \epsilon_i = y_i - \hat{y}_i ϵi=yi−y^i
这里:
- ϵ i \epsilon_i ϵi 是第 ( i i i) 个样本的误差。
- y i y_i yi 是第 ( i i i ) 个样本的实际观测值。
- ( y ^ i \hat{y}_i y^i) 是第 ( i i i ) 个样本的预测值,根据线性回归模型计算得出。
3.3 线性回归误差的高斯分布(正态分布)
假设误差项 (
ϵ
\epsilon
ϵ ) 服从均值为0的正态分布,即 (
ϵ
∼
N
(
0
,
σ
2
)
\epsilon \sim N(0, \sigma^2)
ϵ∼N(0,σ2))。
概率密度函数:[
f
(
ϵ
;
μ
,
σ
2
)
=
1
2
π
σ
2
e
−
(
ϵ
−
μ
)
2
2
σ
2
f(\epsilon; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(\epsilon - \mu)^2}{2\sigma^2}}
f(ϵ;μ,σ2)=2πσ21e−2σ2(ϵ−μ)2 ]
- ( f( ϵ \epsilon ϵ; μ \mu μ, σ 2 \sigma^2 σ2) ) 是误差项 ( ϵ \epsilon ϵ ) 的概率密度函数。
- ( μ \mu μ ) 是误差的均值(在普通最小二乘线性回归中,通常假设 ( μ = 0 \mu = 0 μ=0 ))。
- ( σ 2 \sigma^2 σ2 ) 是误差的方差。
- ( ϵ \epsilon ϵ ) 是单个误差项。
在线性回归中,误差项 ( ϵ \epsilon ϵ) 不一定非得满足高斯分布(正态分布)。然而,在普通最小二乘线性回归(Ordinary Least Squares, OLS)的假设中,通常假定误差项满足以下条件:
- 零均值:误差项的期望值为零,即 ( E ( ϵ ) = 0 E(\epsilon) = 0 E(ϵ)=0 )。
- 同方差性:误差项具有恒定的方差,即 ( V a r ( ϵ i ) = σ 2 Var(\epsilon_i) = \sigma^2 Var(ϵi)=σ2) 对所有 ( i ) 都相同。
- 独立性:误差项之间相互独立,即 ( ϵ i \epsilon_i ϵi ) 和 ( ϵ j \epsilon_j ϵj) 之间不相关,对于 ( i ≠ j i \neq j i=j )。
- 正态分布:误差项通常假定为正态分布,即 ( ϵ ∼ N ( 0 , σ 2 ) \epsilon \sim N(0, \sigma^2) ϵ∼N(0,σ2) )。
3.4 似然函数
解释:什么样的参数跟我们的数据组合后恰好是真实值
对于给定的数据集,似然函数 ( L ) 可以表示为:
L
(
β
)
=
∏
i
=
1
m
P
(
y
i
∣
x
i
,
β
)
L(\beta) = \prod_{i=1}^{m} P(y_i | x_i, \beta)
L(β)=∏i=1mP(yi∣xi,β)。
3.5 对数似然
对数似然 (
ℓ
\ell
ℓ ) 是似然函数的对数,用于简化计算(乘法转换为加法):
ℓ
(
β
)
=
log
L
(
β
)
\ell(\beta) = \log L(\beta)
ℓ(β)=logL(β)。
3.6 目标函数(Loss Function)
线性回归的目标函数通常是最小化均方误差。
[
MSE
(
β
)
=
1
2
m
∑
i
=
1
m
(
y
i
−
(
β
0
+
β
1
x
i
1
+
…
+
β
n
x
i
n
)
)
2
\text{MSE}(\beta) = \frac{1}{2m} \sum_{i=1}^{m} (y_i - (\beta_0 + \beta_1 x_{i1} + \ldots + \beta_n x_{in}))^2
MSE(β)=2m1∑i=1m(yi−(β0+β1xi1+…+βnxin))2]
这里:
- ( MSE ( β ) \text{MSE}(\beta) MSE(β) ) 表示均方误差目标函数。
- ( m m m ) 是样本数量。
- ( y i y_i yi ) 是第 ( i i i ) 个观测值。
- ( β 0 \beta_0 β0) 是截距项。
- ( β 1 , … , β n \beta_1, \ldots, \beta_n β1,…,βn) 是模型参数。
- ( x i 1 , … , x i n x_{i1}, \ldots, x_{in} xi1,…,xin) 是第 ( i ) 个样本的特征值。
在实际应用中,目标函数经常乘以 ( 1 2 \frac{1}{2} 21 ) 以简化梯度计算中的导数,因为 ( ∂ ∂ β ( x 2 ) = 2 x \frac{\partial}{\partial \beta}(x^2) = 2x ∂β∂(x2)=2x ),这样在梯度下降算法中可以省去2的因子。
3.7 最小二乘法
最小二乘法是一种数学优化技术,用于找到最佳拟合曲线的参数。
3.8 梯度下降
梯度下降是一种优化算法,用于最小化目标函数,通常是模型的损失函数。
它通过迭代地调整参数来寻找损失函数的最小值。
MSE
(
β
)
=
1
2
m
∑
i
=
1
m
(
y
i
−
(
β
0
+
x
i
⋅
β
)
)
2
\text{MSE}(\mathbf{\beta}) = \frac{1}{2m} \sum_{i=1}^{m} (y_i - (\beta_0 + \mathbf{x}_i \cdot \mathbf{\beta}))^2
MSE(β)=2m1∑i=1m(yi−(β0+xi⋅β))2
- ( $\text{MSE}(\mathbf{\beta}) ) 是均方误差目标函数。
- ( $m ) 是样本数量。
- ( y i y_i yi ) 是第 ( i i i ) 个观测值。
- ( β 0 \beta_0 β0 ) 是截距项。
- ( x i \mathbf{x}_i xi ) 是第 ( i ) 个样本的特征向量。
- ( β \mathbf{\beta} β ) 是参数向量,包括截距项 ( β 0 \beta_0 β0 ) 和特征权重 ( β 1 , … , β n \beta_1, \ldots, \beta_n β1,…,βn )。
- ( x i ⋅ β \mathbf{x}_i \cdot \mathbf{\beta} xi⋅β ) 表示向量 ( x i \mathbf{x}_i xi ) 和 ( β \mathbf{\beta} β ) 的点积。
请注意,上述公式中的点积 (
x
i
⋅
β
\mathbf{x}_i \cdot \mathbf{\beta}
xi⋅β ) 表示所有特征权重与对应特征值的乘积之和。这种表示方法强调了参数向量和特征向量的运算。

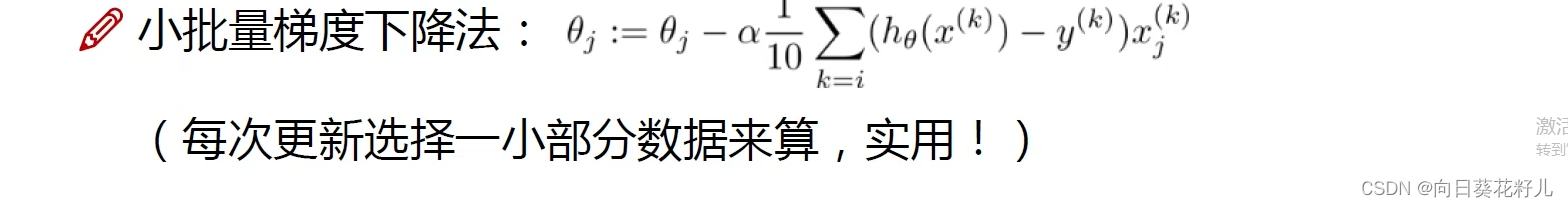
3.8.1 批量梯度下降(Batch Gradient Descent)
每次迭代使用所有样本来更新参数。
3.8.2 随机梯度下降(Stochastic Gradient Descent, SGD)
每次迭代只使用一个样本来更新参数。
3.8.3 小批量梯度下降(Mini-batch Gradient Descent)
每次迭代使用一小部分样本来更新参数。
3.8.4 学习率(Learning Rate)
学习率是梯度下降算法中的一个超参数,用于控制梯度下降中每一步更新参数时的步长。
选择适当的学习率是重要的,因为太大的学习率可能导致跳过最小值甚至发散,而太小的学习率则会导致收敛速度过慢。
对结果会产生巨大影响,一般小一点。
如何选择:从小选择,不行再小()

3.8.5 批处理数量(Batch Size)
批处理数量是指每次迭代中用于更新模型的样本数量。
批处理数量:32,64,128都可以,很多时候还得考虑内存和效率
3.8.6 梯度下降、学习率、批处理数量 之间的关系
看上面【批量梯度下降、随机梯度下降、 小批量梯度下降】的知识点






















 7450
7450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








