openMVG学习笔记

编译运行不同版本流程（调试参数）：

 

openMVG 2.0：openmvg2.0编译与使用_诺有缸的高飞鸟的博客-CSDN博客

openMVG旧版本：openMVG-openMVS的学习和编译_openmvs 编译_11-32的博客-CSDN博客

官方文档：SfM: Structure from Motion — openMVG library

两种主流SFM方法流程介绍：

 几种SFM方法对比：

openMVG输入检测：

测试图片下载链接：https://github.com/openMVG/ImageDataset_SceauxCastle。在初始化图像列表之前需要指定相机焦距f，相机焦距可以由相机物理焦距和像素单位长度计算得到，以photoscan为例，导入的图像尺寸是6000*4000，物理焦距（Focal length）为35mm，像素单位长度Pixel size（mm）为0.006mm,那么焦距f就是35÷0.006=5833.33333。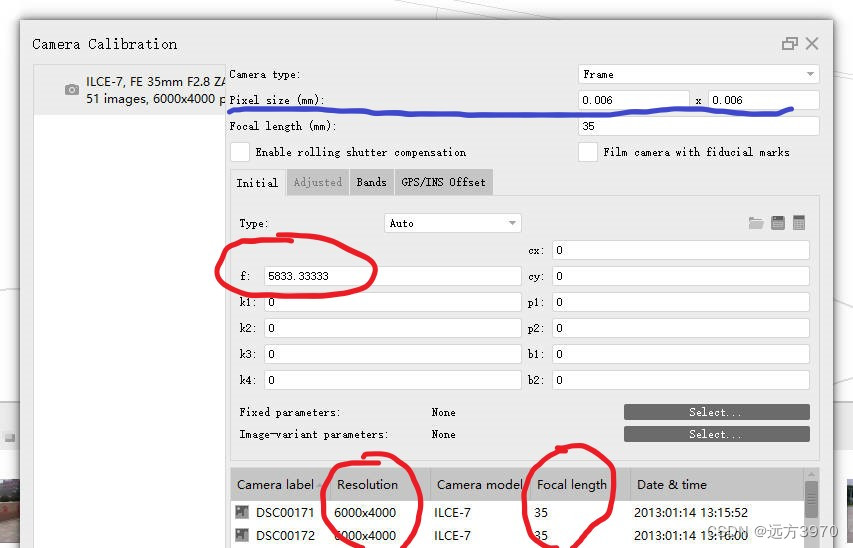

相机内参数:

检查输入端是否有相机内参数矩阵/焦距，注意二者是不可以同时存在的。

若存在相机内参数矩阵，则使用函数checkIntrinsicstringValidity(...)检查是否包含9个参数。

若存在焦距，则从图像的文件头中读取图像的尺寸，由此计算出相机的主点坐标(长、宽的一半)若不存在相机内参数矩阵也不存在焦距，则尝试使用exif工具从图像读取焦距信息，若无法获取，则直接退出。

GPS先验：

使用exif工具从图像中读取GPS信息，并在checkGPS(...)中进行坐标值转换，将GPS的经纬度信息转换为这里主要提供两个坐标系，一个是ECEF(Earth-Centered，Earth-Fixed，地心地固坐标系),另一个是UTM(Universal Transverse Mercator Grid System，通用横墨卡托格网系统)。此外，这里还可以设置GPS各个轴的权重，默认值均为1。

SFM例子：

Library	Address	Type
1DSfM	https://github.com/wilsonkl/SfM_Init	Global SFM
DISCO	http://vision.soic.indiana.edu/projects/disco/	Global SFM
OpenMVG	https://github.com/openMVG/openMVG	Global&Incremental
Theia	https://github.com/sweeneychris/TheiaSfM	Global&Incremental
OpenSfM	https://github.com/mapillary/OpenSfM	Incremental SFM
SAMANTHA	https://www.3dflow.net/technology/3df-samantha/	Hierarchical SFM
Colmap	https://demuc.de/colmap/	Incremental SFM
VisualSFM	http://ccwu.me/vsfm/index.html	Incremental SFM

OpenMVG方法介绍：

计算本质矩阵

①去除弱连接的边，保留影像连接关系图中的最大子图：在影像关系无向图的边集合E中，采用SIFT匹配，若两影像匹配点较少，将边从集合E中剔除。若匹配点数量不少于阈值nMatch1，则利用 RANSAC 算法计算本质矩阵，并分解出影像间的相对旋转矩阵和平移矢量，若用于计算的内点数量少于阈值nMatch2，则认为影像相对位姿不够准确，该像对关联弱，将其剔除。

②根据归一化像点坐标利用 RANSAC 算法计算本质矩阵，对得到的模型进行显著性筛选，对分解得到的R和t即为两摄影机坐标系之间的相对旋转和平移，因此，可以由本质矩阵分解得到两相机相对位置和姿态参数。

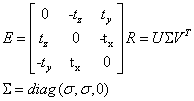
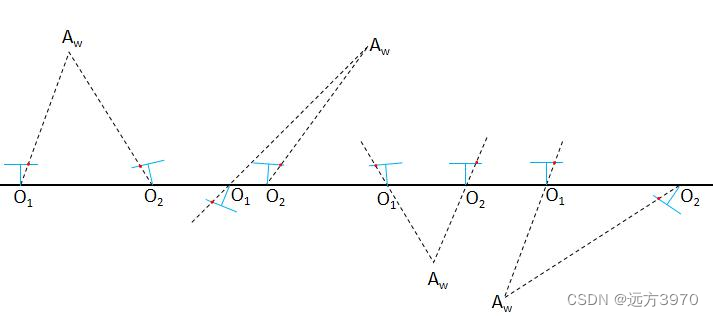
 本质矩阵分解后可以得到四种不同的解：

            

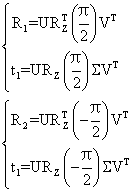
③遍历4组解，基于每组解的结果对所有特征点匹配对进行三角化，并统计三角化出来的内点数量，取内点数量最多的(R,t)作为最终解。

本质矩阵解的约束

旋转平均：

实现了一个L2旋转平均 (L2 Rotation Averaging)算法。该算法的输入是相机数目、相机之间的相对旋转矩阵以及一个空的全局旋转矩阵向量;输出是估计的全局旋转矩阵向量。该算法主要用于多个相机的位姿估计，其中旋转部分由于不可见性等原因难以直接从特征点匹配中得到，需要通过相邻相机之间的关系进行计算。

旋转平均方法采用了线性代数的方法来实现旋转矩阵的平均化。

   首先构建一个稀疏的矩阵A，然后将A的转置矩阵AT与A相乘得到一个对称的正定矩阵ATA。对于 ATA 矩阵，使用自适应特征值分解算法，得到其特征向量和特征值。特征向量构成的矩阵的列即为所有相机的旋转矩阵的一组解，从上一步得到的解向量中选择最优解，具体来说是选择其特征值最小的三个特征向量，通过SVD 分解得到其对应的旋转矩阵。对于上一步得到的旋转矩阵，通过 Gram-Schmidt 正交化方法得到最终的全局旋转矩阵向量。

平移平均：

首先调用Compute_translations函数，该函数使用三角测量的方法计算相对平移。它通过对全局旋转图中的相机姿态进行匹配和特征提取来找到共享的对应点对。找到的对应关系将用于后续的相对平移估计。

Compute_translations：

1、创建一个PairWiseMatches对象map_triplet_matches，存储属于姿态三元组的匹配点对。

遍历匹配提供者提供的匹配点对，筛选出由姿态三元组支持且具有两个不同姿态ID的匹配点对，并将其加入map_triplet_matches中。

使用TracksBuilder对象从map_triplet_matches中构建轨迹，并将轨迹存储到tracks中。

如果轨迹数量少于30个，则返回false。

将图像观测数据转换为三个矩阵x1、x2和x3，用于后续的三角视觉几何求解。

从SfM数据中获取最小的焦距值，用于后续的阈值归一化。

构建三角视觉几何求解器的核心对象kernel，其中包括三个图像观测矩阵、全局旋转矩阵和一个阈值上限。

使用AC-RANSAC算法进行鲁棒估计，得到三个姿态之间的平移矩阵，并更新输出参数。

返回估计结果，如果内点数量大于30和内点数量占总轨迹数量的比例大于0.33，则返回true，否则返回false。

接下来调用Translation_averaging函数，该函数根据初始的相对平移估计结果，利用不同的平移平均方法对全局平移进行估计。根据选择的方法不同，可以使用L1范数、Soft-L1范数或L2范数进行平移平均。最终得到的平移估计结果将用于更新相机姿态。

首先创建了一组配对（pairs），表示视图之间的相对平移。这些配对是从vec_relative_motion_数据结构中提取得到的。随后对相对平移图进行图形清理操作，保留只有最大的双向连接组件。这有助于过滤掉不可靠或异常的平移。

检查经过清理操作后剩余的视图数量（iNview）。如果视图少于3个，则返回false，因为没有足够的视图进行运动平均。

根据所选的平移平均方法（eTranslationAveragingMethod），代码执行不同的平移平均算法。这些算法包括L1范数、Soft L1范数和L2距离（Chordal距离）方法。每种方法根据相对运动数据和其他参数来估计全局平移。

根据估计的全局平移，更新视图的位姿，以使其与估计的相机中心一致。

最后，根据相机姿态的有效性，对匹配关系进行过滤，保留与具有有效姿态的视图相关的匹配。