python平方矩阵 数学最小值解法【简单易懂，代码可以直接运行】

python平方矩阵 数学最小值解法【简单易懂，代码可以直接运行】

首先先解释一些什么是回环矩阵：

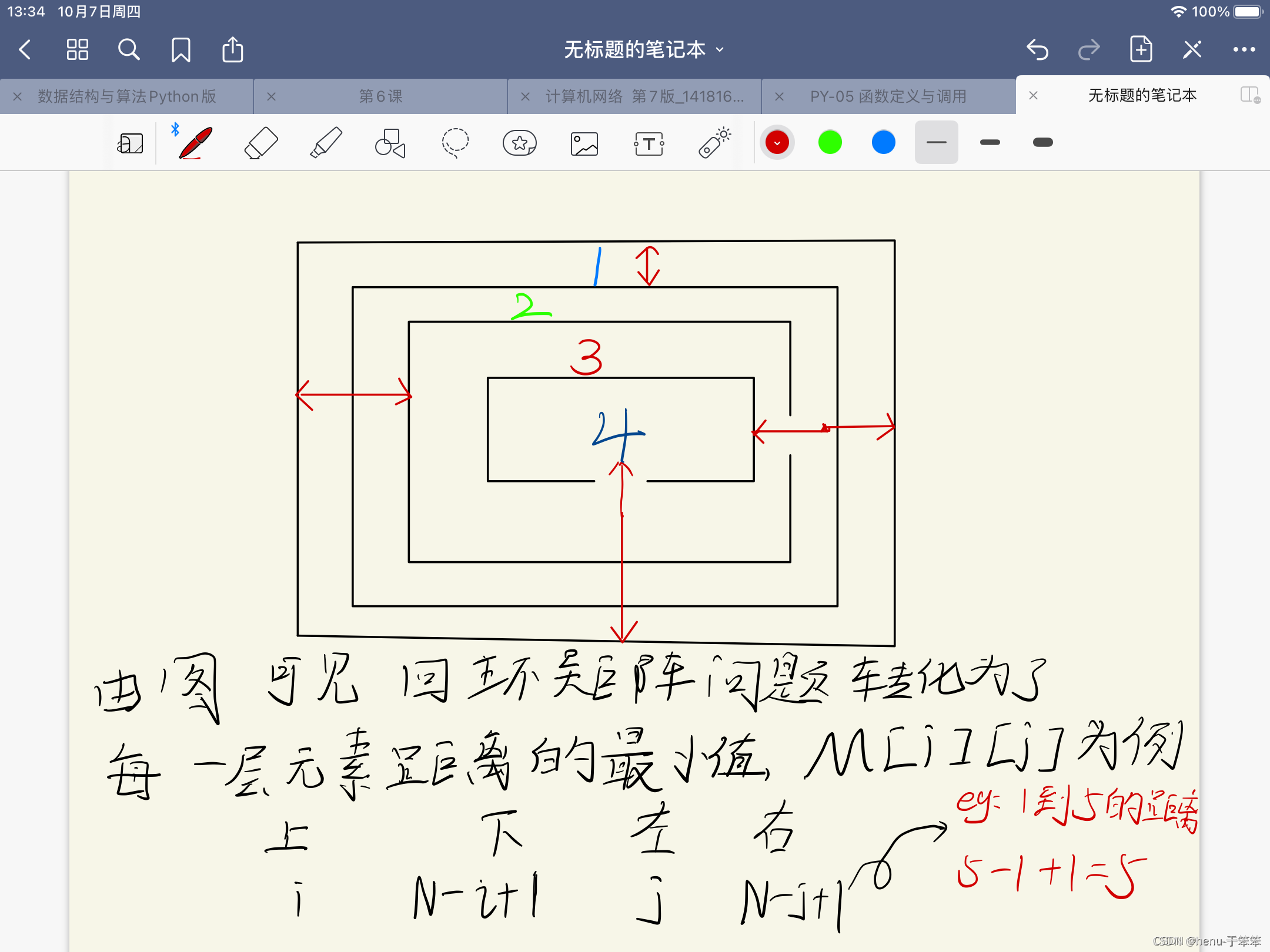
如图所示即是回环矩阵，也是这篇文章里面这道题的解法

输入整数 N，输出一个 N 阶的回字形二维数组。
数组的最外层为 1，次外层为 2，以此类推。
输入格式
输入包含多行，每行包含一个整数 N。
当输入行为 N=0 时，表示输入结束，且该行无需作任何处理。
输出格式
对于每个输入整数 N，输出一个满足要求的 N 阶二维数组。
每个数组占 N 行，每行包含 N 个用空格隔开的整数。
每个数组输出完毕后，输出一个空行。
数据范围
0≤N≤100
对于这道题，如果单纯的用循环来做的话，我觉得是很难找到循环中矩阵中各个值该如何变化，我想用循环赋值，然后利用交换矩阵的行和列的值，来完成i，j处元素关于对角线对称位置元素的值，不过自己用循环想了一个中午也没想出来正确的解法，输出的矩阵中总有几个值不符合输出的要求。
下面介绍一种数学方法来解决这个问题，利用最小值。回环矩阵其实是矩阵中每一层元素到达矩阵边缘的最小值，以M[i][j]为例：

边缘	距离
上边缘	i
下边缘	N-i+1
左边缘	j
右边缘	N-i+1

然后利用min函数找出四者中的最小值，然后输出即可啦
点个👍吧，秋梨膏
代码如下：

#平方矩阵输入的值最外层是1，第二层是2，第三层是3以此类推
#实质上是找每一层的元素到每一条边的最小值
N = eval(input())
while N != 0:
    for i in range(1,N + 1):
        for j in range(1,N + 1):
            up = i
            down = N - i + 1
            left = j
            right = N - j +1
            print(min(min(up,down),min(left,right)),end=' ')
        print()
    print()
    N = eval(input())