1 数组
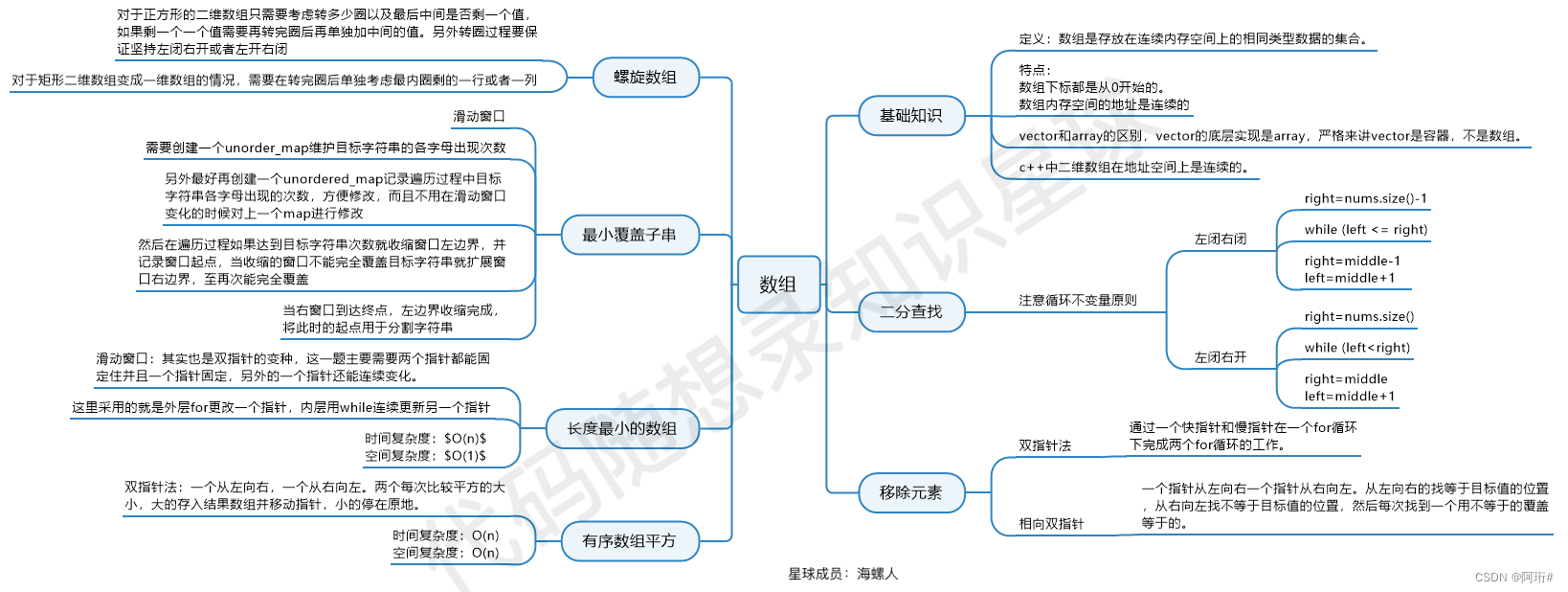
图、知识点、大部分题解源代码随想录
704 二分查找
二分查找的前提：有序数组、无重复元素
二分查找注意事项：
1、中间值mid取法
应该用 mid = l + （r-l）/ 2 ，而不是 mid = (l + r) / 2，因为如果 l 和 r都很大，那么（l + r）将会溢出整数范围。
2、递归结束条件
左边界>有边界
3、边界更新
left=mid+1或right=mid-1
（第二种递归结束和边界更新：while (left >= right)时结束边界，left=mid或right=mid）
我的解法：
时间复杂度 O(logN)： 其中 N 为数组 nums 长度。二分查找使用对数级别时间。
空间复杂度 O(1) ： 变量 i , j 使用常数大小空间。
class Solution:
def search(self, nums: List[int], target: int) -> int:
right = len(nums) - 1
left = 0
self.nums = nums
self.target = target
return self.Recursion(left, right)
def Recursion(self, left, right):
mid = int(left + (right-left)/2)
# 注意递归结束条件
if left > right:
return -1
else:
if self.nums[mid] > self.target:
right = mid - 1
# 一定要注意递归要return啊！！！！！
return self.Recursion(left, right)
elif self.nums[mid] < self.target:
left = mid + 1
return self.Recursion(left, right)
elif self.nums[mid] == self.target:
return mid☆☆☆题解1：更简洁
原来一个while就可以递归quq...
class Solution:
def search(self, nums: List[int], target: int) -> int:
i, j = 0, len(nums) - 1
while i <= j:
# //整数除法，向下取整
m = (i + j) // 2
if nums[m] < target: i = m + 1
elif nums[m] > target: j = m - 1
else: return m
return -135 搜索插入位置
☆☆☆我的解法：二分查找
关键在于不存在时最后的return，最后一轮循环时一定存在left=right=mid，然后分成两种情况讨论，最后的结果都是刚好在left上
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if target > nums[mid]:
left = mid + 1
elif target < nums[mid]:
right = mid - 1
else:
return mid
return left69 x的平方根
☆☆☆我的解法：二分查找
分析思路同35
class Solution:
def mySqrt(self, x: int) -> int:
left, right = 1, x
while left <= right:
mid = left + (right - left) // 2
mid2 = mid * mid
if mid2 < x:
left = mid + 1
elif mid2 > x:
right = mid - 1
else:
return mid
return right367 有效的完全平方数
☆☆☆我的解法：二分查找
class Solution:
def isPerfectSquare(self, num: int) -> bool:
left, right = 1, num
while left <= right:
mid = left + (right - left) // 2
mid2 = mid * mid
if mid2 < num:
left = mid + 1
elif mid2 > num:
right = mid - 1
else:
return True
return False34 在排序数组中查找元素的第一个和最后一个位置
☆☆☆我的解法：二分查找
# 1、首先，在 nums 数组中二分查找 target；
# 2、如果二分查找失败，则 binarySearch 返回 -1，表明 nums 中没有 target。此时，searchRange 直接返回 {-1, -1}；
# 3、如果二分查找成功，则 binarySearch 返回 nums 中值为 target 的一个下标。然后，通过左右滑动指针，来找到符合题意的区间class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
left, right = 0, len(nums) - 1
index = -1
while left <= right:
mid = left + (right - left) // 2
if target < nums[mid]:
right = mid - 1
elif target > nums[mid]:
left = mid + 1
else:
index = mid
break
if index == -1:
return [-1, -1]
i, j = index, index
# 当i-1没有超出边界，且i-1也符合条件时
while i - 1 >= 0 and nums[i-1] == target:
i -= 1
while j + 1 <= len(nums) - 1 and nums[j+1] == target:
j += 1
return [i, j]题解：两个二分查找，分别找左右边界
考虑 target 开始和结束位置，其实我们要找的就是数组中「第一个等于 target 的位置」（记为 leftIdx）和「第一个大于 target 的位置减一」（记为 rightIdx）。
寻找target在数组里的左右边界，有如下三种情况：
- 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
- 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
- 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}
# 解法4
# 1、首先，在 nums 数组中二分查找得到第一个大于等于 target的下标leftBorder；
# 2、在 nums 数组中二分查找得到第一个大于等于 target+1的下标， 减1则得到rightBorder；
# 3、如果开始位置在数组的右边或者不存在target，则返回[-1, -1] 。否则返回[leftBorder, rightBorder]
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
def binarySearch(nums:List[int], target:int) -> int:
left, right = 0, len(nums)-1
while left<=right: # 不变量：左闭右闭区间
middle = left + (right-left) //2
# 这里是>=说明，左边可能还会有target（最差情况也是mid表示的接下来的右边界至少一个相等的），左边还有，所以往左缩小，找左边第一个
if nums[middle] >= target:
right = middle - 1
else: # nums[middle] < target说明左边没有target，左边界也在右边，所以left右移
left = middle + 1
return left # 若存在target，则返回第一个等于target的值
leftBorder = binarySearch(nums, target) # 搜索左边界
rightBorder = binarySearch(nums, target+1) -1 # 搜索右边界
if leftBorder == len(nums) or nums[leftBorder]!= target: # 情况一和情况二
return [-1, -1]
return [leftBorder, rightBorder]
27 移除元素
我的解法：双向指针
思路是双指针指向两边，当左边的元素为目标值，而右边不是目标值时，交换两个元素，当左右下标相遇说明遍历了一遍数组。
需要单独判断空数组是因为最后return时的判断条件nums[left]超出边界了
时间复杂度：O(n)，其中 n 为序列的长度。我们只需要遍历该序列至多一次。
空间复杂度：O(1)。我们只需要常数的空间保存若干变量。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
if len(nums)==0:
return 0
left, right = 0, len(nums)-1
while left < right:
if nums[left] == val:
if nums[right] != val:
# 交换两个元素
nums[left], nums[right] = nums[right], nums[left]
# python没有自增自减运算符！！！
left = left + 1
right = right - 1
else :
right = right - 1
else:
left = left + 1
return left+1 if nums[left]!=val else left☆☆☆题解：双指针法（快慢指针法）
也是双指针但是都是从前往后移动：
- 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
- 慢指针：指向更新 新数组下标的位置
让 a 一直往后移动，相当于 nums[a] 从数组第一个数遍历到最后一个数。
当且仅当我们发现 nums[a] != val 的时候，我们把这个数拷贝到 b 指向的位置，默认 b 是从 0 开始的，然后 b += 1 指向下一个位置。
时间复杂度：O(n)，其中 n 为序列的长度。我们只需要遍历该序列至多两次。
空间复杂度：O(1)。我们只需要常数的空间保存若干变量。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
# 快慢指针
fast = 0 # 快指针
slow = 0 # 慢指针
size = len(nums)
while fast < size: # 不加等于是因为，a = size 时，nums[a] 会越界
# slow 用来收集不等于 val 的值，如果 fast 对应值不等于 val，则把它与 slow 替换
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow☆☆☆题解2：更好的双向指针法
无需单独判断空数组
# 相向双指针法
# 时间复杂度 O(n)
# 空间复杂度 O(1)
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
n = len(nums)
left, right = 0, n - 1
while left <= right:
while left <= right and nums[left] != val:
left += 1
while left <= right and nums[right] == val:
right -= 1
if left < right:
nums[left] = nums[right]
left += 1
right -= 1
return left
26 删除排序数组中的重复项
我的解法：pop
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
i = 0
while i < len(nums):
if i+1 < len(nums) and nums[i+1] == nums[i]:
nums.pop(i+1)
elif i+1 < len(nums) and nums[i+1] != nums[i]:
i += 1
else:
return len(nums)
return 0☆☆☆题解：双指针
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
# 从1下标开始，因为如果数组只有一个元素，它自己肯定不会重复
fast = slow = 1
while fast < n:
# 注意是和fast-1比
if nums[fast] != nums[fast - 1]:
nums[slow] = nums[fast]
slow += 1
fast += 1
# 返回slow，slow是下标，下标-1+1表示元素个数，即slow
return slow283 移动零
☆☆☆我的解法：双指针（不简洁danwon方法）
图源：
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
i, j = 0, 0
while j < len(nums):
# 找到最左边的0
if i + 1 < len(nums) and nums[i] != 0:
i += 1
# j一定在i的右侧
j = i + 1
continue
# 找到0右边的非零数，交换
if nums[j] != 0:
nums[i], nums[j] = nums[j], nums[i]
j += 1
i += 1
else:
j += 1844 比较含退格的字符串
我的解法：求最终s和t然后比较
class Solution:
def backspaceCompare(self, s: str, t: str) -> bool:
i, j = 0, 0
s = list(s)
t = list(t)
while i < len(s):
if s[i] == "#" and i>0:
s.pop(i)
s.pop(i-1)
i = i - 1
elif s[i] == "#" and i==0:
s.pop(i)
else:
i += 1
while j < len(t):
if t[j] == "#" and j>0:
t.pop(j)
t.pop(j-1)
j = j - 1
elif t[j] == "#" and j==0:
t.pop(j)
else:
j += 1
return True if s == t else False☆☆☆题解：双指针从后往前遍历
class Solution:
def backspaceCompare(self, S: str, T: str) -> bool:
i, j = len(S) - 1, len(T) - 1
skipS = skipT = 0
while i >= 0 or j >= 0:
while i >= 0:
if S[i] == "#":
skipS += 1
i -= 1
elif skipS > 0:# 不是退格且skip不空，则当前元素应该被跳过
skipS -= 1
i -= 1
else:# 不是空格，且skip空，当前元素应该保留去做对比
break
while j >= 0:# T同理
if T[j] == "#":
skipT += 1
j -= 1
elif skipT > 0:
skipT -= 1
j -= 1
else:
break
if i >= 0 and j >= 0:
if S[i] != T[j]:
return False
elif i >= 0 or j >= 0:
return False
i -= 1
j -= 1
return True
作者：御三五 🥇
链接：https://leetcode.cn/problems/backspace-string-compare/solutions/683776/shuang-zhi-zhen-bi-jiao-han-tui-ge-de-zi-8fn8/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。977 有序数组的平方
我的解法：暴力排序
先平方后排序，时间复杂度是 O(n + nlogn)， 可以说是O(nlogn)的时间复杂度
时间复杂度：O(nlogn)，其中 n 是数组 nums 的长度。
空间复杂度：O(logn)。除了存储答案的数组以外，我们需要 O(logn) 的栈空间进行排序。
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
nums[i] = nums[i] ** 2
nums.sort()
return nums☆☆☆题解：双指针——归并排序
数组其实是有序的， 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。
此时可以考虑双指针法了，i指向起始位置，j指向终止位置。
定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
时间复杂度：O(n)，其中 n 是数组 nums 的长度。
空间复杂度：O(1)。除了存储答案的数组以外，我们只需要维护常量空间。
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
n = len(nums)
# 需要提前定义列表，用来存放结果
ans = [0] * n
i, j = 0, n - 1
# for循环：n-1,n-2,n-3...0，即从n-1到-1的左闭右开，即n-1到0的左闭右闭区间
for p in range(n - 1, -1, -1):
x = nums[i] * nums[i]
y = nums[j] * nums[j]
if x > y: # 更大的数放右边
ans[p] = x
# x是统计负数的，指针从左向右走
i += 1
else:
ans[p] = y
# x是统计正数的，指针从右向左走
j -= 1
return ans题解2：暴力排序+列表推导法
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
return sorted(x*x for x in nums)209 长度最小的子数组
我的解法：暴力法
两个指针，一个记录子数组首元素下标，另一个记录子数组尾元素下标，两个for循环
时间复杂度：O(n2)，其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标，对于每个开始下标，需要遍历其后面的下标得到长度最小的子数组。
空间复杂度：O(1)。
未通过，18测试用例会超时...
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
Min = 1000
Sum = 0
i,j = 0,0
for i in range(len(nums)):
for j in range(i, len(nums)):
Sum += nums[j]
if Sum >= target
if j-i+1 < Min:
Min = j-i+1
break
else:
continue
Sum = 0
return Min if Min<1000 else 0☆☆☆题解：滑动窗口
时间复杂度：O(n)，其中 n 是数组的长度。指针 start 和 end 最多各移动 n 次。
空间复杂度：O(1)。
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
l = len(nums)
left = 0
right = 0
min_len = float('inf')
cur_sum = 0 #当前的累加值
while right < l:# 遍历表示结束的指针
cur_sum += nums[right]
while cur_sum >= s: # 当前累加值大于目标值
min_len = min(min_len, right - left + 1)
cur_sum -= nums[left]# 窗口累加值缩小
left += 1# 窗口缩小，缩小后继续判断cur_sum >= s，直到不满足为止再前移结束指针
right += 1# 前移结束指针
return min_len if min_len != float('inf') else 0滑动窗口：
所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。
滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口，主要确定如下三点：
- 窗口内是什么？
- 如何移动窗口的起始位置？
- 如何移动窗口的结束位置？
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动：如果当前窗口的值大于等于s了，窗口就要向前移动了（也就是该缩小了），然后判断是否满足窗口，若满足，继续缩小（起始位置向前移动），若不满足，结束位置前移（即窗口扩大）。
窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
为什么时间复杂度是O(n)。
不要以为for里放一个while就以为是O(n^2)啊， 主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。
题解2：前缀+二分查找（不如滑动窗口）
方法一的时间复杂度是 O(n2)，因为在确定每个子数组的开始下标后，找到长度最小的子数组需要 O(n)的时间。如果使用二分查找，则可以将时间优化到 O(logn)。
为了使用二分查找，需要额外创建一个数组 sums 用于存储数组 nums 的前缀和，其中 sums[i] 表示从 nums[0]到 nums[i−1] 的元素和。得到前缀和之后，对于每个开始下标 i，可通过二分查找得到大于或等于 i 的最小下标 bound\，使得 sums[bound]−sums[i−1]≥s，并更新子数组的最小长度（此时子数组的长度是 bound−(i−1)）。
因为这道题保证了数组中每个元素都为正，所以前缀和一定是递增的，这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正，这里就不能使用二分来查找这个位置了。
现成的库和函数来为我们实现这里二分查找大于等于某个数的第一个位置的功能，Python 中的 bisect.bisect_left
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
ans = n + 1
sums = [0]
for i in range(n):
sums.append(sums[-1] + nums[i])
for i in range(1, n + 1):
target = s + sums[i - 1]# s是目标值，target是满足 目标值 + i-1前缀和 的bound前缀和
bound = bisect.bisect_left(sums, target)
if bound != len(sums):# 下标没有len(nums)
ans = min(ans, bound - (i - 1))
return 0 if ans == n + 1 else ans904 水果成篮
☆☆☆我的解法：滑动窗口
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
length = 0
left, right = 0, 0
kind = dict()
while right < len(fruits):
kind[fruits[right]] = kind.get(fruits[right],0) + 1
while len(kind.keys()) > 2:
if kind[fruits[left]] > 1:
kind[fruits[left]] -= 1
else:
kind.pop(fruits[left])
left += 1
if right-left+1>length:
length = right-left+1
right += 1
return length79 最小覆盖子串
我的解法：滑动窗口
class Solution:
def minWindow(self, s: str, t: str) -> str:
left, right = 0, 0
son = dict()
ton = list(t)
MIN = s+'A'
td = dict()
for i in ton:
td[i] = td.get(i,0)+1
while right < len(s):
son[s[right]] = son.get(s[right],0) + 1
# 左一定要小于右 并且（左不在t中 或者 左在t中但数量超了）
while left<right and ((s[left] not in ton) or son[s[left]]>td[s[left]]):
if son[s[left]] > 1:
son[s[left]] -= 1
else:
son.pop(s[left])
left += 1
# 长度小 并且 t中的每个都有
if right - left +1 < len(MIN) and all(son.get(i,0)>=td[i] for i in ton):
MIN = "".join(s[left:right+1])
right +=1
return MIN if len(MIN)<=len(s) else ""题解：滑动窗口
class Solution:
def minWindow(self, s: str, t: str) -> str:
ans_left, ans_right = -1, len(s)
left = 0
# counter计数器，是dict的子类
cnt_s = Counter() # s 子串字母的出现次数
cnt_t = Counter(t) # t 中字母的出现次数
for right, c in enumerate(s): # 移动子串右端点
cnt_s[c] += 1 # 右端点字母移入子串
# 这里居然能直接比较！！！（python 3.10 以上才行）
# 考虑满足的时候就滑出直到不满足 而不是滑到满足
while cnt_s >= cnt_t: # 涵盖
if right - left < ans_right - ans_left: # 找到更短的子串
ans_left, ans_right = left, right # 记录此时的左右端点
cnt_s[s[left]] -= 1 # 左端点字母移出子串
left += 1 # 移动子串左端点
return "" if ans_left < 0 else s[ans_left: ans_right + 1]
作者：灵茶山艾府
链接：https://leetcode.cn/problems/minimum-window-substring/solutions/2713911/liang-chong-fang-fa-cong-o52mn-dao-omnfu-3ezz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。☆☆☆题解2：滑动窗口（优化）
看代码就懂了，less指的是t的元素，在s的子串中数量不够的有几个，比如s的子串是abcdef，t是aaack，那么less=2，因为a和k数量不够。
class Solution:
def minWindow(self, s: str, t: str) -> str:
ans_left, ans_right = -1, len(s)
left = 0
cnt_s = Counter() # s 子串字母的出现次数
cnt_t = Counter(t) # t 中字母的出现次数
less = len(cnt_t) # 有 less 种字母的出现次数 < t 中的字母出现次数
for right, c in enumerate(s): # 移动子串右端点
cnt_s[c] += 1 # 右端点字母移入子串
if cnt_s[c] == cnt_t[c]:
less -= 1 # c 的出现次数从 < 变成 >=
while less == 0: # 涵盖：所有字母的出现次数都是 >=
if right - left < ans_right - ans_left: # 找到更短的子串
ans_left, ans_right = left, right # 记录此时的左右端点
x = s[left] # 左端点字母
if cnt_s[x] == cnt_t[x]:
less += 1 # x 的出现次数从 >= 变成 <（下一行代码执行后）
cnt_s[x] -= 1 # 左端点字母移出子串
left += 1 # 移动子串左端点
return "" if ans_left < 0 else s[ans_left: ans_right + 1]
作者：灵茶山艾府
链接：https://leetcode.cn/problems/minimum-window-substring/solutions/2713911/liang-chong-fang-fa-cong-o52mn-dao-omnfu-3ezz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。59 螺旋矩阵II
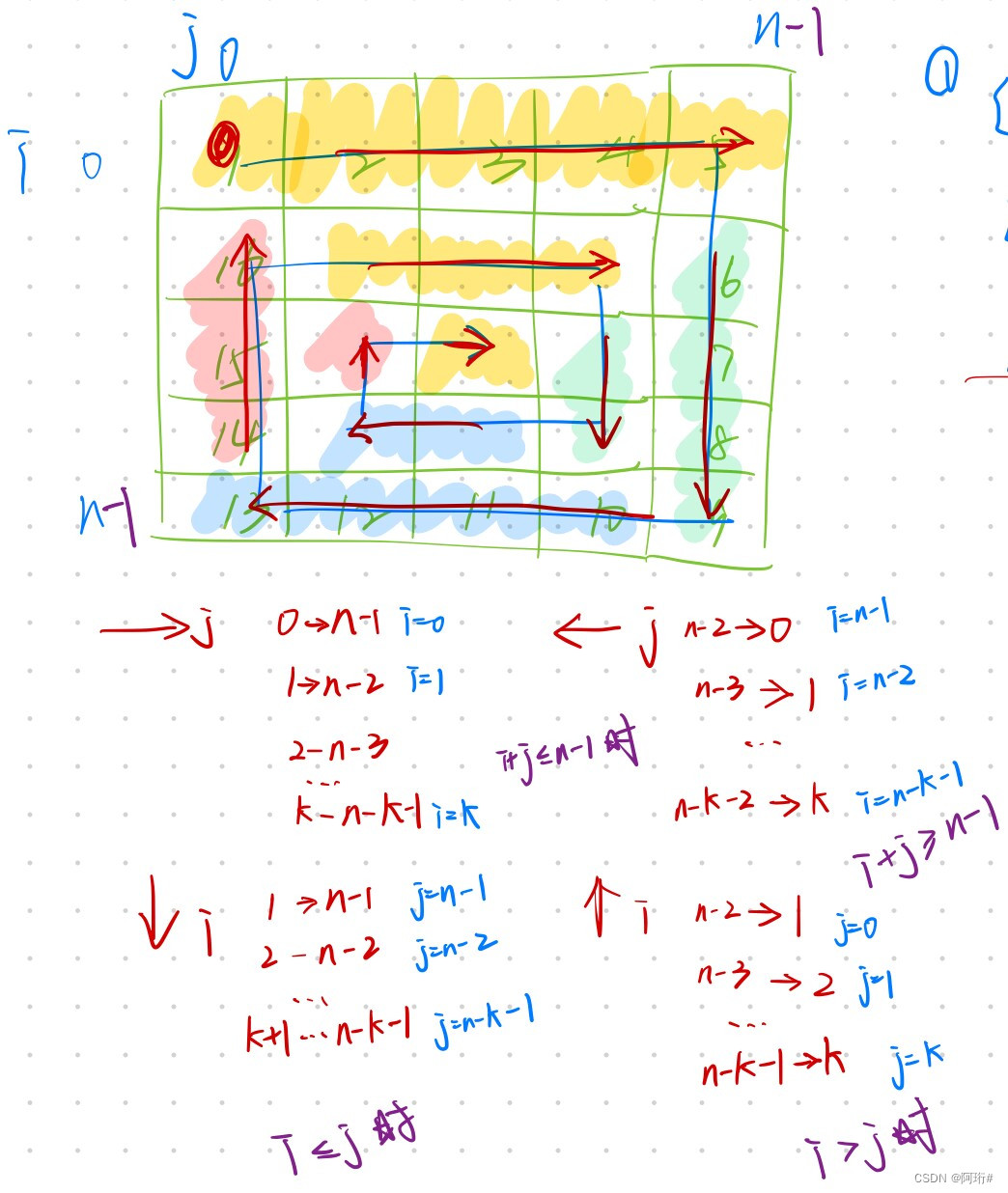
我的解法：找规律（左开右闭）
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
# 创建二维空列表
l1 = [[] for i in range(n)]
for i in range(n):
l1[i] = [None] * n
i, j, k = 0, 0, 1
while k <= n ** 2:
# →
while i + j <= n - 1 :
l1[i][j] = k
k += 1
j += 1
j -= 1
i += 1
# ↓
while i <= j :
l1[i][j] = k
k += 1
i += 1
i -= 1
j -= 1
# ←
while i + j >= n - 1 :
l1[i][j] = k
k += 1
j -= 1
j += 1
i -= 1
# ↑
while i > j :
l1[i][j] = k
k += 1
i -= 1
i += 1
j += 1
return l1☆☆☆题解：左闭右开原则
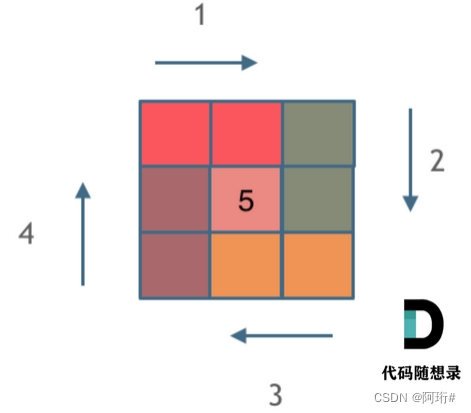
这里每一种颜色，代表一条边，我们遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。
这也是坚持了每条边左闭右开的原则。
- 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
- 空间复杂度 O(1)
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
nums = [[0] * n for _ in range(n)]
startx, starty = 0, 0 # 起始点
loop, mid = n // 2, n // 2 # 迭代次数、n为奇数时，矩阵的中心点
count = 1 # 计数
for offset in range(1, loop + 1) : # 每循环一层偏移量加1，偏移量从1开始
for i in range(starty, n - offset) : # 从左至右，左闭右开
nums[startx][i] = count
count += 1
for i in range(startx, n - offset) : # 从上至下
nums[i][n - offset] = count
count += 1
for i in range(n - offset, starty, -1) : # 从右至左
nums[n - offset][i] = count
count += 1
for i in range(n - offset, startx, -1) : # 从下至上
nums[i][starty] = count
count += 1
startx += 1 # 更新起始点
starty += 1
if n % 2 != 0 : # n为奇数时，填充中心点
nums[mid][mid] = count
return nums题解2：定义四个边界
好像和我的思路差不多，左开右闭，for循环比我写的while好...
class Solution(object):
def generateMatrix(self, n):
if n <= 0:
return []
# 初始化 n x n 矩阵
matrix = [[0]*n for _ in range(n)]
# 初始化边界和起始值
top, bottom, left, right = 0, n-1, 0, n-1
num = 1
while top <= bottom and left <= right:
# 从左到右填充上边界
for i in range(left, right + 1):
matrix[top][i] = num
num += 1
top += 1
# 从上到下填充右边界
for i in range(top, bottom + 1):
matrix[i][right] = num
num += 1
right -= 1
# 从右到左填充下边界
for i in range(right, left - 1, -1):
matrix[bottom][i] = num
num += 1
bottom -= 1
# 从下到上填充左边界
for i in range(bottom, top - 1, -1):
matrix[i][left] = num
num += 1
left += 1
return matrix54 螺旋矩阵
我的解法：左闭右开
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
res = []
row, column = len(matrix), len(matrix[0])
starx, stary = 0, 0
count, offset = 0, 0
while count < row* column-1:
offset += 1
for i in range(stary, column-offset):
res.append(matrix[starx][i])
count += 1
if count == row * column:
break
for i in range(starx, row-offset):
res.append(matrix[i][column-offset])
count += 1
if count == row * column:
break
for i in range(column-offset, stary, -1):
res.append(matrix[row-offset][i])
count += 1
if count == row * column:
break
for i in range(row-offset, starx, -1):
res.append(matrix[i][stary])
count += 1
if count == row * column:
break
starx += 1
stary += 1
if column == row and row %2!=0:
res.append(matrix[row//2][row//2])
# while len(res)>row* column:
# res.pop()
return res☆☆☆题解：左开右闭（除第一行），比较边界相遇情况
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix: return []
l, r, t, b, res = 0, len(matrix[0]) - 1, 0, len(matrix) - 1, []
while True:
for i in range(l, r + 1): res.append(matrix[t][i]) # left to right
t += 1
if t > b: break
for i in range(t, b + 1): res.append(matrix[i][r]) # top to bottom
r -= 1
if l > r: break
for i in range(r, l - 1, -1): res.append(matrix[b][i]) # right to left
b -= 1
if t > b: break
for i in range(b, t - 1, -1): res.append(matrix[i][l]) # bottom to top
l += 1
if l > r: break
return res
作者：Krahets
链接：https://leetcode.cn/problems/spiral-matrix/solutions/2362055/54-luo-xuan-ju-zhen-mo-ni-qing-xi-tu-jie-juvi/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。LCR 146 螺旋遍历二维数组 （和54一模一样）
我的解法：
class Solution:
def spiralArray(self, array: List[List[int]]) -> List[int]:
if not array:
return []
left, right = 0, len(array[0])-1
top, bottom = 0, len(array)-1
res = []
while True:
for i in range(left, right+1):
res.append(array[top][i])
top += 1
if top > bottom:
break
for i in range(top,bottom+1):
res.append(array[i][right])
right -= 1
if left > right:
break
for i in range(right, left-1,-1):
res.append(array[bottom][i])
bottom -= 1
if top > bottom:
break
for i in range(bottom,top-1,-1):
res.append(array[i][left])
left += 1
if left > right:
break
return res
2 链表
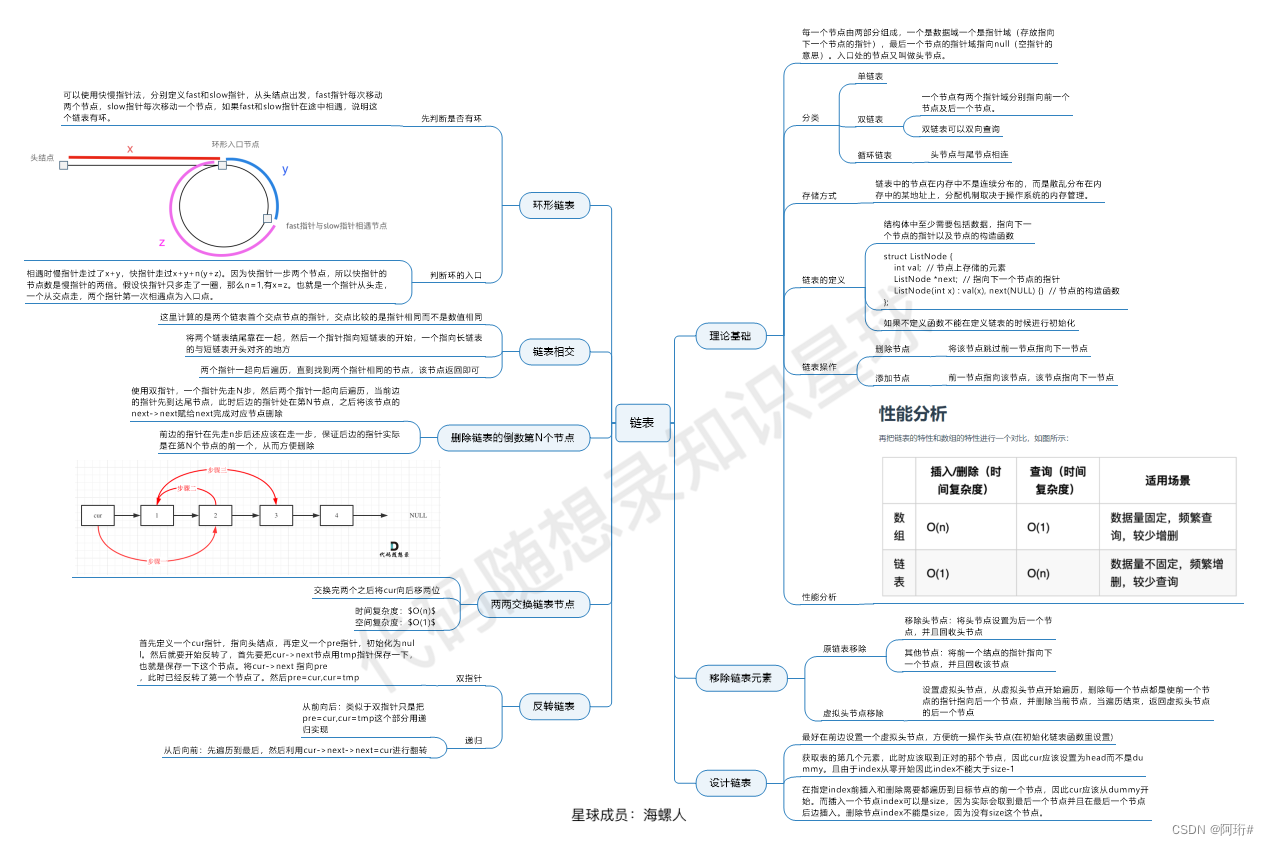
tips：
- 许多操作需要单独处理头结点，或设置虚拟头结点统一解决
知识点：
链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。
链表的入口节点称为链表的头结点也就是head。
链表中的节点在内存中不是连续分布的 ，而是散乱分布在内存中的某地址上。
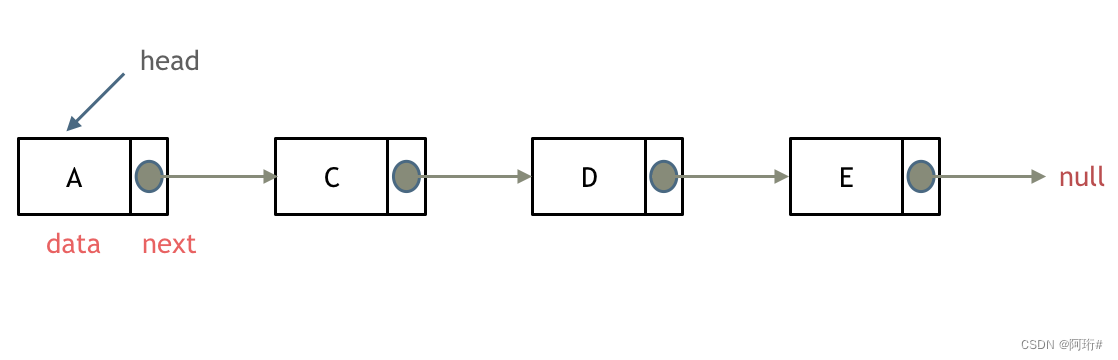
- 单链表：
单链表中的指针域只能指向节点的下一个节点。
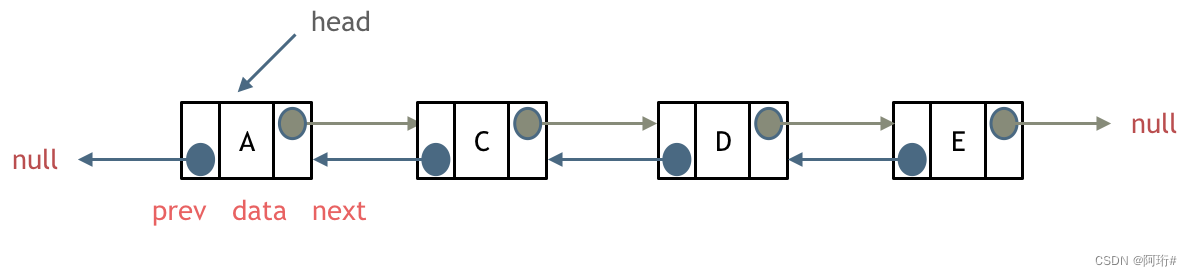
- 双链表：
每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。
双链表 既可以向前查询也可以向后查询。
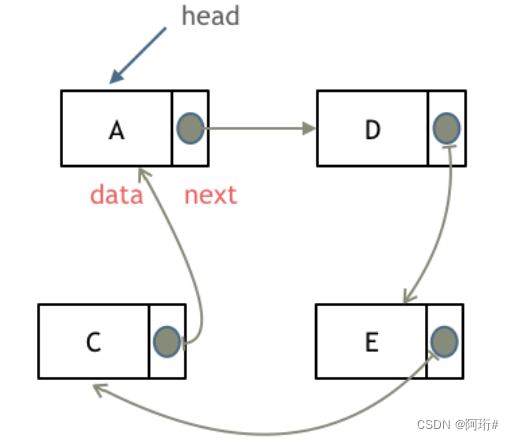
- 循环链表
链表首尾相连。循环链表可以用来解决约瑟夫环问题。
- 删除节点
只要将C节点的next指针 指向E节点就可以了。
Python有自己的内存回收机制，不用自己手动释放D。
要是删除第五个节点，需要从头节点查找到第四个节点通过next指针进行删除操作，查找的时间复杂度是O(n)。
- 添加节点
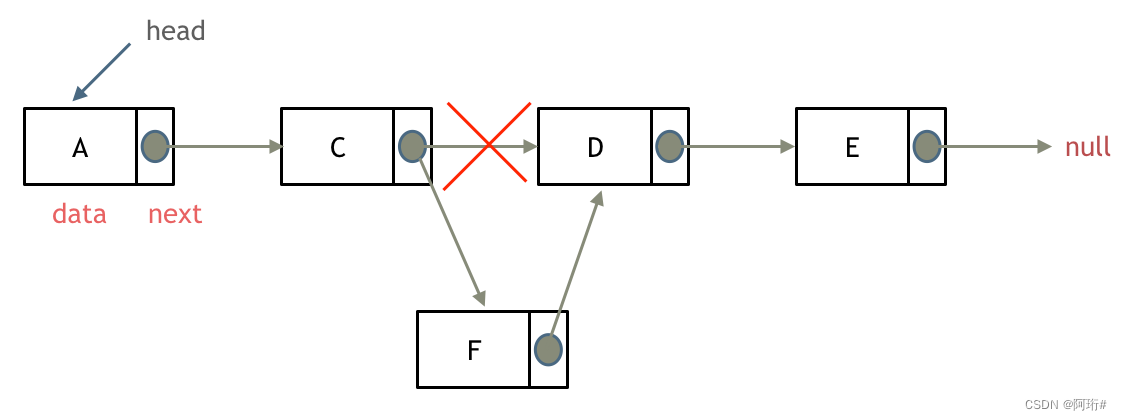
- 与数组对比
数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。
链表的长度可以是不固定的，并且可以动态增删， 适合数据量不固定，频繁增删，较少查询的场景。
- python定义链表：
用类
class ListNode:
def __init__(self, val, next=None):
self.val = val
self.next = next
203 移除链表元素
我的题解：单独处理头结点
写的太复杂了
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
while head:
if head.val == val:
head = head.next
else:
break
n_node = head
if n_node:
while n_node.next:
if n_node.next.val != val:
n_node = n_node.next
else:
n_node.next = n_node.next.next
return head
else:
return None☆☆☆题解：虚拟头结点
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
# 创建虚拟头部节点以简化删除过程
dummy_head = ListNode(next = head)
# 遍历列表并删除值为val的节点
current = dummy_head
while current.next:
if current.next.val == val:
current.next = current.next.next
else:
current = current.next
return dummy_head.next
707 设计链表
我的题解：单链表，创建了虚拟头结点
注意查询、添加、删除的题目要求，需要比较index和链表长度
class ListNode:
def __init__(self, val = 0, next = None):
self.val = val
self.next = next
class MyLinkedList:
def __init__(self):
self.dummy_head = ListNode()
self.len = 0
def get(self, index: int) -> int:
current = self.dummy_head
if index < self.len:
for i in range(0, index):
current = current.next
return current.next.val
else:
return -1
def addAtHead(self, val: int) -> None:
new_head = ListNode(val, self.dummy_head.next)
self.dummy_head.next = new_head
self.len += 1
def addAtTail(self, val: int) -> None:
current = self.dummy_head
while current.next:
current = current.next
new_tail = ListNode(val, None)
current.next = new_tail
self.len += 1
def addAtIndex(self, index: int, val: int) -> None:
current = self.dummy_head
if index <= self.len:
for i in range(0, index):
current = current.next
new_node = ListNode(val, current.next)
current.next = new_node
self.len += 1
def deleteAtIndex(self, index: int) -> None:
current = self.dummy_head
if index < self.len:
for i in range(0, index):
current = current.next
current.next = current.next.next
self.len -= 1
# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)☆☆☆题解：单链表
这个对index的判断更加严谨，创建新节点直接赋值更方便
（版本一）单链表法
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class MyLinkedList:
def __init__(self):
self.dummy_head = ListNode()
self.size = 0
def get(self, index: int) -> int:
if index < 0 or index >= self.size:
return -1
current = self.dummy_head.next
for i in range(index):
current = current.next
return current.val
def addAtHead(self, val: int) -> None:
self.dummy_head.next = ListNode(val, self.dummy_head.next)
self.size += 1
def addAtTail(self, val: int) -> None:
current = self.dummy_head
while current.next:
current = current.next
current.next = ListNode(val)
self.size += 1
def addAtIndex(self, index: int, val: int) -> None:
if index < 0 or index > self.size:
return
current = self.dummy_head
for i in range(index):
current = current.next
current.next = ListNode(val, current.next)
self.size += 1
def deleteAtIndex(self, index: int) -> None:
if index < 0 or index >= self.size:
return
current = self.dummy_head
for i in range(index):
current = current.next
current.next = current.next.next
self.size -= 1
# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)☆☆☆题解2：双链表
class ListNode:
def __init__(self, val=0, prev=None, next=None):
self.val = val
self.prev = prev
self.next = next
class MyLinkedList:
def __init__(self):
# 要同时记住头和尾巴是哪个节点
self.head = None
self.tail = None
self.size = 0
def get(self, index: int) -> int:
if index < 0 or index >= self.size:
return -1
# 判断离头近还是离尾近，节约耗时
if index < self.size // 2:
current = self.head
for i in range(index):
current = current.next
else:
current = self.tail
for i in range(self.size - index - 1):
current = current.prev
return current.val
def addAtHead(self, val: int) -> None:
# 创建自身指针
new_node = ListNode(val, None, self.head)
if self.head:# 已经有头结点
# 更新后节点的指针
self.head.prev = new_node
else:# 没有头结点，新加入的既是头也是尾
self.tail = new_node
# 更新头结点
self.head = new_node
self.size += 1
def addAtTail(self, val: int) -> None:
# 创建自身指针
new_node = ListNode(val, self.tail, None)
if self.tail:
# 更新前节点的指针
self.tail.next = new_node
else:
self.head = new_node
# 更新尾巴结点
self.tail = new_node
self.size += 1
def addAtIndex(self, index: int, val: int) -> None:
if index < 0 or index > self.size:
return
if index == 0:
self.addAtHead(val)
elif index == self.size:
self.addAtTail(val)
else:
if index < self.size // 2:
current = self.head
for i in range(index - 1):
current = current.next
else:
current = self.tail
for i in range(self.size - index):
current = current.prev
# 创建自身指针
new_node = ListNode(val, current, current.next)
# 更新前后节点的指针
current.next.prev = new_node
current.next = new_node
self.size += 1
def deleteAtIndex(self, index: int) -> None:
if index < 0 or index >= self.size:
return
if index == 0:
# 删除当前节点
self.head = self.head.next
if self.head:
# 后面还有其他节点，更新后节点指针
self.head.prev = None
else:
self.tail = None
elif index == self.size - 1:
# 删除当前节点
self.tail = self.tail.prev
if self.tail:
# 前面还有其他节点，更新前节点指针
self.tail.next = None
else:
self.head = None
else:
if index < self.size // 2:
current = self.head
for i in range(index):
current = current.next
else:
current = self.tail
for i in range(self.size - index - 1):
current = current.prev
# 前后节点相连
current.prev.next = current.next
current.next.prev = current.prev
self.size -= 1
# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)206 反转链表
我的题解：双指针迭代
从前往后反转，head单独处理（看题解1吧，我这个写的好多此一举）
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
current = head
pre = None
if head:
while current.next:
ne = current.next
current.next = pre
# 顺移pre和current
pre = current
current = ne
current.next = pre
return current
else:
return head☆☆☆题解1：双指针
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
cur = head
pre = None
while cur:
temp = cur.next # 保存一下 cur的下一个节点，因为接下来要改变cur->next
cur.next = pre #反转
#更新pre、cur指针
pre = cur
cur = temp
return pre题解2：递归
从前往后翻，同双指针法
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
return self.reverse(head, None)
def reverse(self, cur: ListNode, pre: ListNode) -> ListNode:
if cur == None:
return pre
temp = cur.next
cur.next = pre
return self.reverse(temp, cur)24 两两交换链表中的节点
我的题解：
注意：每次交换有三个指针需要改变，第一个节点的next、第二个节点的next、前面节点的next
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
dummy_head = ListNode(next = head)
current = head
i = 0
while current:
if current.next:
current = self.changeTwo(current, current.next)
if i == 0:
# 更新头结点
dummy_head.next = current
i = 1
else:
# 更新前节点的指针
pre.next = current
pre = current.next
current = current.next.next
else:
break
return dummy_head.next
def changeTwo(self, fir, sec):
fir.next = sec.next
sec.next = fir
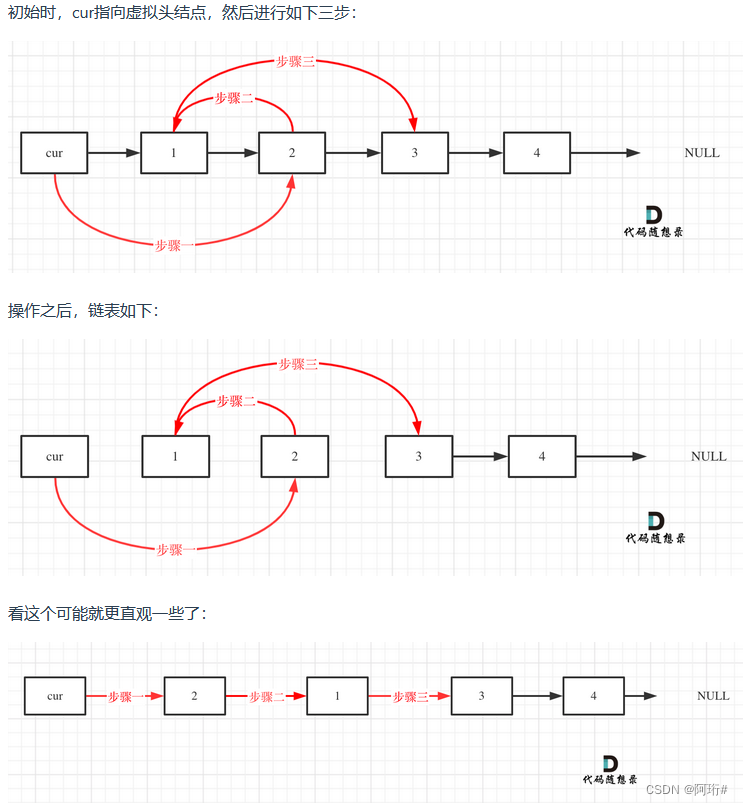
return sec☆☆☆题解：更简洁
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
dummy_head = ListNode(next=head)
current = dummy_head
# 必须有cur的下一个和下下个才能交换，否则说明已经交换结束了
while current.next and current.next.next:
temp = current.next # 防止节点修改
temp1 = current.next.next.next
# crr指向2
current.next = current.next.next
# 2指向1
current.next.next = temp
# 1指向3
temp.next = temp1
# curr顺移
current = current.next.next
return dummy_head.next
题解2：递归！！！！
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
if head is None or head.next is None:
return head
# 待翻转的两个node分别是pre和cur
pre = head
cur = head.next
next = head.next.next
cur.next = pre # 交换
pre.next = self.swapPairs(next) # 将以next为head的后续链表两两交换
# 返回的是交换后的位于前面的节点
return cur19 删除链表的倒数第N个节点
我的题解：笨方法
先遍历计算链表长度，再遍历找到目标节点
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
virtual_head = ListNode(next = head)
current = head
num = 0
while current:
num += 1
current = current.next
if n <= num:
current = virtual_head
for i in range(num - n):
current = current.next
current.next = current.next.next
return virtual_head.next☆☆☆题解：双指针
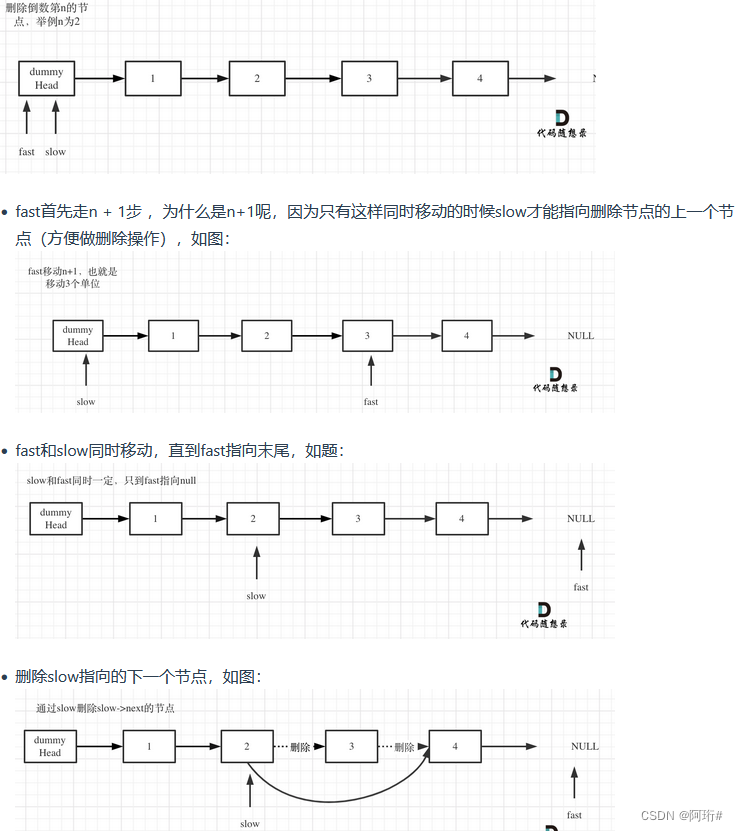
双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。
注意：先让fast先走n步，再让slow出发，这样保证fast走到结尾时，slow刚好位于要删掉的n处，但删除操作需要用到前一个节点，因此slow应该再晚一步出发，即fast先走n+1步
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
# 创建一个虚拟节点，并将其下一个指针设置为链表的头部
dummy_head = ListNode(0, head)
# 创建两个指针，慢指针和快指针，并将它们初始化为虚拟节点
slow = fast = dummy_head
# 快指针比慢指针快 n+1 步
for i in range(n+1):
fast = fast.next
# 移动两个指针，直到快速指针到达链表的末尾
while fast:
slow = slow.next
fast = fast.next
# 通过更新第 (n-1) 个节点的 next 指针删除第 n 个节点
slow.next = slow.next.next
return dummy_head.next
☆☆☆题解2：栈
在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 nnn 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。这样一来，删除操作就变得十分方便了。
用list实现栈！！！
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
dummy = ListNode(0, head)
stack = list()
cur = dummy
while cur:
stack.append(cur)
cur = cur.next
for i in range(n):# 弹出n个元素
stack.pop()
prev = stack[-1]# 最后一个就是第n-1个元素
prev.next = prev.next.next
return dummy.next面试题 02.07. 链表相交
我的题解：
分别统计两个链表长度，然后将长的推进，再同时向前比较节点是否相等，注意是比较节点，而不是节点的值和指针
（注释的是哈希表方法，43用例超时了）
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
# hash_Table = dict()
# currentA = headA
# i = 0
# while currentA:
# hash_Table[i] = currentA
# i += 1
# currentA = currentA.next
# currentB = headB
# while currentB:
# if currentB in hash_Table.values():
# return currentB
# currentB = currentB.next
# return None
nA, nB = 0, 0
currentA = headA
while currentA:
nA += 1
currentA = currentA.next
currentB = headB
while currentB:
nB += 1
currentB = currentB.next
if nA >= nB:
currentLang = headA
currentShort = headB
n = nA -nB
else:
currentLang = headB
currentShort = headA
n = nB -nA
for i in range(n):
currentLang = currentLang.next
while currentShort:
if currentLang == currentShort:
return currentLang
currentLang = currentLang.next
currentShort = currentShort.next
return None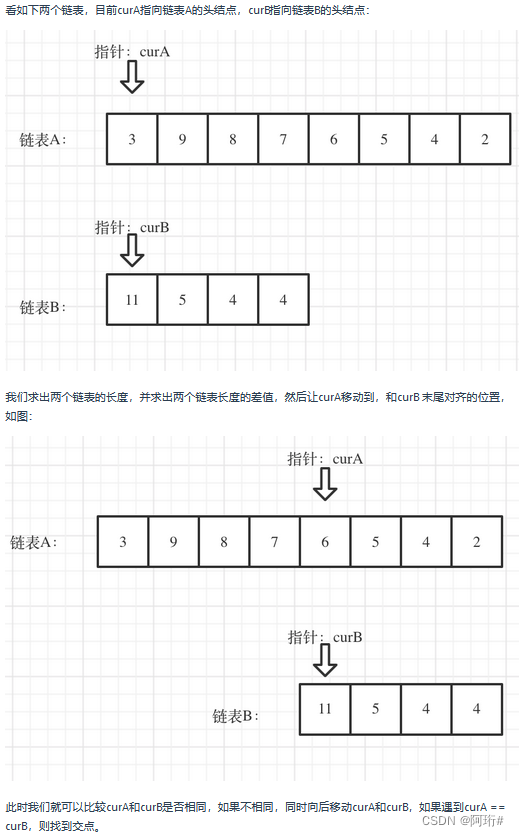
☆☆☆题解：代码复用精简
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
dis = self.getLength(headA) - self.getLength(headB)
# 通过移动较长的链表，使两链表长度相等
if dis > 0:
headA = self.moveForward(headA, dis)
else:
headB = self.moveForward(headB, abs(dis))
# 将两个头向前移动，直到它们相交
while headA and headB:
if headA == headB:
return headA
headA = headA.next
headB = headB.next
return None
def getLength(self, head: ListNode) -> int:
length = 0
while head:
length += 1
head = head.next
return length
def moveForward(self, head: ListNode, steps: int) -> ListNode:
while steps > 0:
head = head.next
steps -= 1
return head题解2：等比例法，没懂
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
# 处理边缘情况——任一个是空链表
if not headA or not headB:
return None
# 在每个链表的头部初始化两个指针
pointerA = headA
pointerB = headB
# 遍历两个链表直到指针相交
while pointerA != pointerB:
# 将指针向前移动一个节点
# ？？？？？
pointerA = pointerA.next if pointerA else headB
pointerB = pointerB.next if pointerB else headA
# 如果相交，指针将位于交点节点，如果没有交点，值为None
return pointerA142 环形链表ii
我的题解：字典哈希表
慢的要死
时间复杂度：O(N)，其中 N 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。
空间复杂度：O(N)，其中 N 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
hash_Table = dict()
current = head
i = 0
while current:
if current in hash_Table.values():
return current
hash_Table[i] = current
i += 1
current = current.next
return None☆☆☆题解：双指针法
1.判断有环
使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。
fast指针一定先进入环中，如果fast指针和slow指针相遇的话，一定是在环中相遇，这是毋庸置疑的。
2.找入口
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。
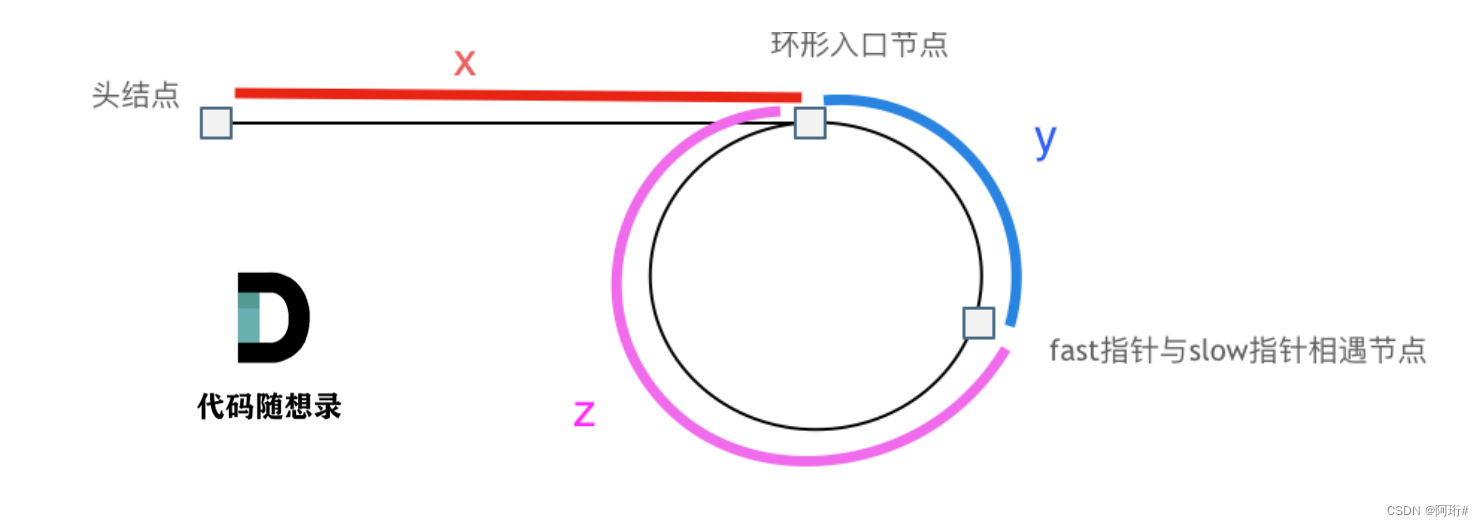
那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针， （y+z）为 一圈内节点的个数A。
为什么第一次在环中相遇，slow的 步数 是 x+y 而不是 x + 若干环的长度 + y 呢？
首先slow进环的时候，fast一定是先进环来了。
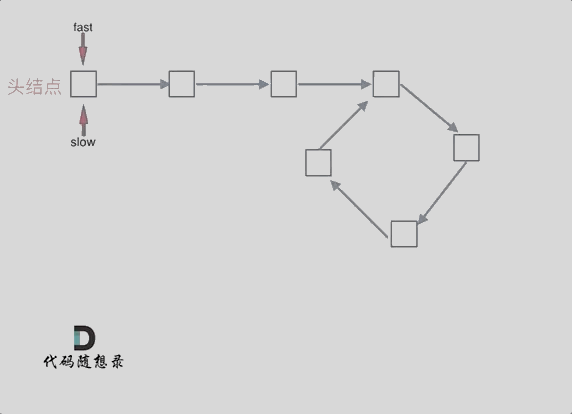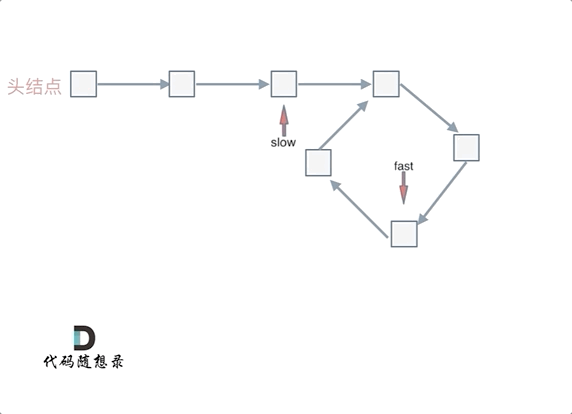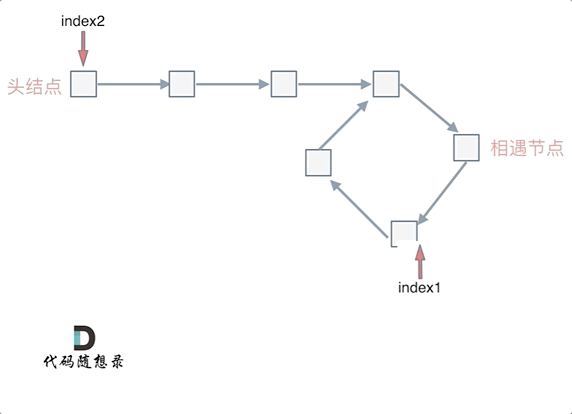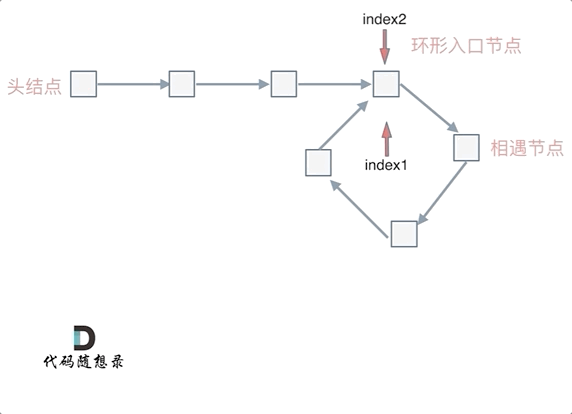
如果slow进环入口，fast也在环入口，那么把这个环展开成直线，就是如下图的样子：
可以看出如果slow 和 fast同时在环入口开始走，一定会在环入口3相遇，slow走了一圈，fast走了两圈。
重点来了，slow进环的时候，fast一定是在环的任意一个位置，如图：
那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。
因为k是小于n的（图中可以看出），所以(k + n) / 2 一定小于n。
也就是说slow一定没有走到环入口3，而fast已经到环入口3了。
这说明什么呢？
在slow开始走的那一环已经和fast相遇了。
那有同学又说了，为什么fast不能跳过去呢？ 在刚刚已经说过一次了，fast相对于slow是一次移动一个节点，所以不可能跳过去。
因为fast指针是一步走两个节点，slow指针一步走一个节点， 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：
(x + y) * 2 = x + y + n (y + z)
即x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。
先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。
当 n为1的时候，公式就化解为 x = z，
这就意味着，从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。
也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。
让index1和index2同时移动，每次移动一个节点， 那么他们相遇的地方就是 环形入口的节点。
那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。
其实这种情况和n为1的时候 效果是一样的，一样可以通过这个方法找到 环形的入口节点，只不过，index1 指针在环里 多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。
- 时间复杂度: O(n)，快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
- 空间复杂度: O(1)
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# If there is a cycle, the slow and fast pointers will eventually meet
if slow == fast:
# Move one of the pointers back to the start of the list
slow = head
while slow != fast:
slow = slow.next
fast = fast.next
return slow
# If there is no cycle, return None
return None题解2：集合哈希表
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
visited = set()
while head:
if head in visited:
return head
visited.add(head)
head = head.next
return None3 哈希表
哈希表（散列表）——用来快速判断一个元素是否出现集合里。
数组哈希表：哈希表中关键码就是数组的索引下标，然后通过下标直接访问数组中的元素
哈希函数：将元素映射到哈希表上
哈希碰撞：拉链法（同一位置用链表串联）、线性探测法（冲突元素顺移到附近位置）
哈希表一般用：数组（有序可变）（关键码是数组下标，存储的数据是数组下标对应位置的元素）、集合（无序可变）、字典（有序可变）（关键码是字典key，存储的数据是对应的value）
tips：
1.数组就是简单的哈希表，但是数组的大小可不是无限开辟的
2.如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费！
3.不重复——用set
4.需要计数（下标）——字典、数组
5.像字母这种区间小且连续的——数组
6.不需要索引下标，且要求不重复的（三数之和、四数之和），哈希表很难（去重效率低）可以试试双指针
242 有效的字母异位词
我的解法：字典哈希表
时间O(n)，空间O(n)
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
hashTable = dict()
# 将s存进哈希表，key是字母，value是出现次数
for i in range(len(s)):
if s[i] in hashTable:
hashTable[s[i]] += 1
else:
hashTable[s[i]] = 1
# 检查t的字母是否都在哈希表中，一旦不在立刻返回false
for j in range(len(t)):
if t[j] in hashTable:
hashTable[t[j]] -= 1
else:
return False
# 内置函数all()判断哈希表的value全为0（说明s有的t都有），时间复杂度还是O(n)
return all(item == 0 for item in hashTable.values())☆☆☆题解1：数组哈希表
时间复杂度：O(n)，其中 n 为 s 的长度。
空间复杂度：O(S)，其中 S 为字符集大小，此处 S=26。
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
record = [0] * 26
for i in s:
#并不需要记住字符a的ASCII，只要求出一个相对数值就可以了
record[ord(i) - ord("a")] += 1
for i in t:
record[ord(i) - ord("a")] -= 1
for i in range(26):
if record[i] != 0:
#record数组如果有的元素不为零0，说明字符串s和t 一定是谁多了字符或者谁少了字符。
return False
return True
题解2：defaultdict()
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
from collections import defaultdict
# int作为defaultdict的初始化函数参数，即字典的value是一个int类型
s_dict = defaultdict(int)
t_dict = defaultdict(int)
for x in s:
s_dict[x] += 1
for x in t:
t_dict[x] += 1
# 字典能用==！！！！！！！！
return s_dict == t_dict题解3：counter()
class Solution(object):
def isAnagram(self, s: str, t: str) -> bool:
from collections import Counter
# 把待计数的数据传给Counter计数器，它即可立即返回一个计数器对象，完成对元素的计数。
# 类似于自己建字典计数的方法
a_count = Counter(s)
b_count = Counter(t)
return a_count == b_count49 字母异位词分组
☆☆☆题解：排序
将排序之后的字符串作为哈希表的键。
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
# 用defaultdict创建字典，value默认是列表
mp = collections.defaultdict(list)
for st in strs:
key = "".join(sorted(st))
mp[key].append(st)
return list(mp.values())题解2：计数
将每个字母出现的次数使用字符串表示，作为哈希表的键。
由于字符串只包含小写字母，因此对于每个字符串，可以使用长度为 26 的数组记录每个字母出现的次数。
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
mp = collections.defaultdict(list)
for st in strs:
counts = [0] * 26
for ch in st:
counts[ord(ch) - ord("a")] += 1
# 需要将 list 转换成 tuple 才能进行哈希
mp[tuple(counts)].append(st)
return list(mp.values())438 找到字符串中所有字母与异位词
我的解法：排序（46测试用例出错）
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
n = len(p)
sorted(p)
res = []
for i in range(len(s) - n +1):
temp = s[i:n+i]
if "".join(sorted(temp)) == p:
res.append(i)
return res☆☆☆题解：滑动窗口+数组
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
n, m, res = len(s), len(p), []
if n < m: return res
p_cnt = [0] * 26
s_cnt = [0] * 26
for i in range(m):
# 初始化滑动窗口
p_cnt[ord(p[i]) - ord('a')] += 1
s_cnt[ord(s[i]) - ord('a')] += 1
if s_cnt == p_cnt:
res.append(0)
for i in range(m, n):
# 开始滑动，一出一进
s_cnt[ord(s[i - m]) - ord('a')] -= 1
s_cnt[ord(s[i]) - ord('a')] += 1
if s_cnt == p_cnt:
res.append(i - m + 1)
return res
题解2：滑动窗口+双指针
...
首先，right一定比left走的快，然后我们考虑两种情况，一，如果运气比较好，第一轮left没有移动，right移动到（right-left+1==m)位置正好满足了，我们加入一个result，然后继续移动right，这个时候，维护的串中一定存在多余的元素，如果新加入的char有用（是p的元素），left需要移动到去除之前相同有用的char的位置，如果新加入的char无用（不是p的元素），left会移动到right位置（说明整个窗口都废了：原本就不行，加了一个没用的更不行了，所以窗口从0开始or原本好的已经记下了，新来的不行，说明整段没用了，所以从0开始），至此，开始重复之前的状态（元素不够一直右移）。二，如果运气不好，在移动的过程中，维护的串中一定会出现某个char不在串p中，这个时候，left也会不断移动直到right的位置，这样和情况一是一样的。
在一个和p长度相同的窗口内，每一个字母的数量都不大于p中该字母的数量，而它们的和又等于p的长度，那就只有一种可能，就是各个字母的数量和p中该字母的数量相等，所以就是p的异位词。
1.元素不够——窗口肯定不符合条件——左窗口不变，右边扩大
2.元素超了——窗口有没用的元素（1>0）或有用的元素超了——窗口要缩小，左边界缩到没用的元素消失或重复的有用的元素减少直到刚好该元素个数刚好符合——都是左边界左移到right对应元素减少到指定条件
3.元素个数刚好符合时或右边界右移过程中判断窗口长度——刚好为异位词
...
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
n, m, res = len(s), len(p), []
if n < m: return res
#设置两个数组，分别用来记录字符串s和字符串p中子母的出现个数
#需要注意的是，这两个数组的索引分别对应着当前字符与字符a的ASCII码的差
p_cnt = [0] * 26
s_cnt = [0] * 26
for i in range(m):
#统计p字符串，例如p=‘abc'，此时p_count=[1,1,1,0,0...]
p_cnt[ord(p[i]) - ord('a')] += 1
#采用滑动窗口的方式，遍历s
#需要注意的是：left，right表示的是在字符串s中的索引；cur_left,cur_right表示的是字符串s中索引为left和right的字符在数组中的索引。
left = 0
for right in range(n):
#边遍历字符串s，边更新s_cnt
cur_right = ord(s[right]) - ord('a')
s_cnt[cur_right] += 1
#当我们发现数量不对时(可以简单理解为滑动窗口大小>固定窗口大小了，此时需要移动左窗口，在这里是一个道理)
while s_cnt[cur_right] > p_cnt[cur_right]:
cur_left = ord(s[left]) - ord('a')
s_cnt[cur_left] -= 1
left += 1
#如果我们发现数量正好，则满足异位词的条件，将左窗口位置加入结果列表即可
if right - left + 1 == m:
res.append(left)
return res
作者：郁郁雨
链接：https://leetcode.cn/problems/find-all-anagrams-in-a-string/submissions/545506491/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。349 两个数组的交集
如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。
此时就要使用另一种结构体了，set
（直接使用set 不仅占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。）
我的题解：字典哈希表
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
hash_table = dict()
l1 = []
for i in range(len(nums1)):
hash_table[nums1[i]] = 1
for j in range(len(nums2)):
if nums2[j] in hash_table:
hash_table[nums2[j]] +=1
for key, value in hash_table.items():
if value >1:
l1.append(key)
return l1☆☆☆题解：使用字典和集合
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
# 使用哈希表存储一个数组中的所有元素
table = {}
for num in nums1:
# get()获取value，不存在则返回0
table[num] = table.get(num, 0) + 1
# 使用集合存储结果
res = set()
for num in nums2:
if num in table:
res.add(num)
# 这里有必要删除吗？
del table[num]
return list(res)
题解2：使用数组哈希表
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
# 需要题目上限个数组空间
count1 = [0]*1001
count2 = [0]*1001
result = []
for i in range(len(nums1)):
count1[nums1[i]]+=1
for j in range(len(nums2)):
count2[nums2[j]]+=1
for k in range(1001):
# 都不是0
if count1[k]*count2[k]>0:
result.append(k)
return result题解3：集合
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
# & 取集合的并集
return list(set(nums1) & set(nums2))350 两个数组的交集II
☆☆☆我的解法1：字典哈希表
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
hash_table = dict()
res = []
for i in nums1:
hash_table[i] = hash_table.get(i,0) + 1
for j in nums2:
if j in hash_table and hash_table[j] > 0:
hash_table[j] -= 1
res.append(j)
return res我的解法2：排序+双指针
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
res = []
nums1.sort()
nums2.sort()
i, j = 0, 0
while i < len(nums1) and j < len(nums2):
if nums1[i] > nums2[j]:
j += 1
elif nums1[i] < nums2[j]:
i += 1
else:
res.append(nums1[i])
j += 1
i += 1
return res202 快乐数
三种可能。
- 最终会得到 111。
- 最终会进入循环。
- 值会越来越大，最后接近无穷大。
对于 3 位数的数字，它不可能大于 243。这意味着它要么被困在 243 以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道，最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种选择。
即使在代码中你不需要处理第三种情况，你仍然需要理解为什么它永远不会发生，这样你就可以证明为什么你不处理它。
时间O(logn)，空间O(logn)
我的题解：字典哈希表
对于这种只关心出现了，不关心出现次数，无需计算的情况，集合比字典更好用
class Solution:
def isHappy(self, n: int) -> bool:
hash_table = dict()
while n != 1:
# 判断位数
s = len(str(n))
sum1 = 0
for i in range(s):
# 得到最后一位数字
sum1 += (n % 10) ** 2
# 除法 向下取整（即整体右移一位）
n = n // 10
# sum1在哈希表中存在，说明已经开始循环了，则false
if sum1 in hash_table:
return False
# 存入哈希表
hash_table[sum1] = 1
n = sum1
return True题解：集合
class Solution:
def isHappy(self, n: int) -> bool:
record = set()
while True:
n = self.get_sum(n)
if n == 1:
return True
# 如果中间结果重复出现，说明陷入死循环了，该数不是快乐数
if n in record:
return False
else:
record.add(n)
def get_sum(self,n: int) -> int:
new_num = 0
while n:
# divmod()获取商和余数
n, r = divmod(n, 10)
new_num += r ** 2
return new_num题解2：集合
class Solution:
def isHappy(self, n: int) -> bool:
record = set()
while n not in record:
record.add(n)
new_num = 0
n_str = str(n)
# 另一种计算每位平方和的方法
for i in n_str:
new_num+=int(i)**2
if new_num==1: return True
else: n = new_num
return False
题解3：使用数组
class Solution:
def isHappy(self, n: int) -> bool:
record = []
while n not in record:
record.append(n)
new_num = 0
n_str = str(n)
for i in n_str:
new_num+=int(i)**2
if new_num==1: return True
else: n = new_num
return False
题解4：精简集合
class Solution:
def isHappy(self, n: int) -> bool:
seen = set()
while n != 1:
# 这个推导式好诶
n = sum(int(i) ** 2 for i in str(n))
if n in seen:
return False
seen.add(n)
return True
题解5：精简数组
class Solution:
def isHappy(self, n: int) -> bool:
seen = []
while n != 1:
n = sum(int(i) ** 2 for i in str(n))
if n in seen:
return False
seen.append(n)
return True
☆☆☆题解6：快慢指针法
时间复杂度：O(logn)，空间复杂度：O(1)
通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针，但数据仍然形成链表结构。
意识到我们实际有个链表，那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法。这个算法是两个奔跑选手，一个跑的快，一个跑得慢。在龟兔赛跑的寓言中，跑的慢的称为 “乌龟”，跑得快的称为 “兔子”。
不管乌龟和兔子在循环中从哪里开始，它们最终都会相遇。这是因为兔子每走一步就向乌龟靠近一个节点（在它们的移动方向上）。
我们不是只跟踪链表中的一个值，而是跟踪两个值，称为快跑者和慢跑者。在算法的每一步中，慢速在链表中前进 1 个节点，快跑者前进 2 个节点（对 getNext(n) 函数的嵌套调用）。
如果 n 是一个快乐数，即没有循环，那么快跑者最终会比慢跑者先到达数字 1。
如果 n 不是一个快乐的数字，那么最终快跑者和慢跑者将在同一个数字上相遇。
class Solution:
def isHappy(self, n: int) -> bool:
slow = n
fast = n
# 如果 n 是一个快乐数，即没有循环，那么快跑者最终会比慢跑者先到达数字 1。
while self.get_sum(fast) != 1 and self.get_sum(self.get_sum(fast)):
# 慢跑者，每次跑一步
slow = self.get_sum(slow)
# 快跑者，每次跑两步
fast = self.get_sum(self.get_sum(fast))
# 如果 n 不是一个快乐的数字，那么最终快跑者和慢跑者将在同一个数字上相遇。
if slow == fast:
return False
return True
def get_sum(self,n: int) -> int:
new_num = 0
while n:
n, r = divmod(n, 10)
new_num += r ** 2
return new_num1.两数之和
我的解法：暴力枚举
时间O(n2)，空间O(1)
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for f_index, first in enumerate(nums):
for s_index, second in enumerate(nums[f_index+1:]):
if first + second ==target:
return [f_index, s_index + f_index + 1]
else:
continue
题解1：哈希表
class Solution(object):
def twoSum(self, nums, target):
# 遍历列表
for i in range(len(nums)):
# 计算需要找到的下一个目标数字
res = target-nums[i]
# 遍历剩下的元素，查找是否存在该数字
if res in nums[i+1:]:
# 若存在，返回答案。这里由于是两数之和，可采用.index()方法
# 获得目标元素在nums[i+1:]这个子数组中的索引后，还需加上i+1才是该元素在nums中的索引
return [i, nums[i+1:].index(res)+i+1]☆☆☆题解2：哈希表
时间O(n)，空间O(n)，相对于暴力枚举属于空间（哈希表的开销）换时间（O(1)寻找target-x）
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
# 创建哈希表（使用dict函数创建空字典）
# 哈希表的关键码（字典的key）是nums元素值，通过关键码得到存储的该元素下标（value）
hashtable = dict()
for i, num in enumerate(nums):
# 判断target-x是否已经在哈希表中，在字典的键中寻找target-x
if target - num in hashtable:
# 即针对当前的x，存在target-x在哈希表中
#（实际上在前面已经把第一个数遍历过然后存入哈希表了，继续遍历找到了当前的第二个数）
# 发现存在，则返回哈希表中target-x（key）对应的下标（value），和当前第二个数的下标
return [hashtable[target - num], i]
# 判断完target-x是否存在后，将x存入哈希表（字典的key是x的值，value是x的下标）
hashtable[nums[i]] = i
return []454 四数相加II
我的题解：两个字典哈希表
时间O(n2)，空间O(n2)
class Solution:
def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:
# 1和2的和存起来，3和4的结果存起来，其中结果相同的对应计数增加
# 在两个和中应用两数之和的哈希表，并且对应计数相乘得到该情况的组合数量
count = 0
Hash_Table1, Hash_Table2 = dict(), dict()
for i in range(len(nums1)):
for j in range(len(nums2)):
if nums1[i] + nums2[j] in Hash_Table1:
Hash_Table1[nums1[i] + nums2[j]] += 1
else:
Hash_Table1[nums1[i] + nums2[j]] = 1
for i in range(len(nums3)):
for j in range(len(nums4)):
if nums3[i] + nums4[j] in Hash_Table2:
Hash_Table2[nums3[i] + nums4[j]] += 1
else:
Hash_Table2[nums3[i] + nums4[j]] = 1
for i in Hash_Table1:
if 0 - i in Hash_Table2:
count += Hash_Table1[i] * Hash_Table2[0 - i]
return count☆☆☆题解：更简洁精炼的字典哈希表
class Solution(object):
def fourSumCount(self, nums1, nums2, nums3, nums4):
# 使用字典存储nums1和nums2中的元素及其和
hashmap = dict()
# 这个列表遍历比我的好太多了.....
for n1 in nums1:
for n2 in nums2:
# get()函数用的也很好......
hashmap[n1+n2] = hashmap.get(n1+n2, 0) + 1
# 如果 -(n1+n2) 存在于nums3和nums4, 存入结果
count = 0
for n3 in nums3:
for n4 in nums4:
key = - n3 - n4
if key in hashmap:
count += hashmap[key]
return count题解2：counter()
class Solution:
def fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:
countAB = collections.Counter(u + v for u in A for v in B)
ans = 0
# counter是dict子类，可以使用dict的遍历方法
for u in C:
for v in D:
if -u - v in countAB:
ans += countAB[-u - v]
return ans383 赎金信
我的题解：字典哈希表
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
# magazine建表
Hash_Table = dict()
for i in magazine:
Hash_Table[i] = Hash_Table.get(i, 0) + 1
for j in ransomNote:
if j in Hash_Table and Hash_Table[j] != 0:
Hash_Table[j] -= 1
else:
return False
return True☆☆☆题解：数组哈希表
因为题目说只有小写字母，那可以采用空间换取时间的哈希策略，用一个长度为26的数组来记录magazine里字母出现的次数。
然后再用ransomNote去验证这个数组是否包含了ransomNote所需要的所有字母。
依然是数组在哈希法中的应用。
一些同学可能想，用数组干啥，都用map完事了，其实在本题的情况下，使用map的空间消耗要比数组大一些的，因为map要维护红黑树或者哈希表，而且还要做哈希函数，是费时的！数据量大的话就能体现出来差别了。 所以数组更加简单直接有效！
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
ransom_count = [0] * 26
magazine_count = [0] * 26
for c in ransomNote:
ransom_count[ord(c) - ord('a')] += 1
for c in magazine:
magazine_count[ord(c) - ord('a')] += 1
return all(ransom_count[i] <= magazine_count[i] for i in range(26))
题解2：使用Counter
from collections import Counter
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
# ransomNote的元素及个数要小于等于magazine的
return not Counter(ransomNote) - Counter(magazine)
题解3：使用count
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
return all(ransomNote.count(c) <= magazine.count(c) for c in set(ransomNote))
题解4：使用count(简单易懂，题解3的详细描述)
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
for char in ransomNote:
if char in magazine and ransomNote.count(char) <= magazine.count(char):
continue
else:
return False
return True
15 三数之和
两数之和 就不能使用双指针法，因为1.两数之和要求返回的是索引下标， 而双指针法一定要排序，一旦排序之后原数组的索引就被改变了。
如果1.两数之和要求返回的是数值的话，就可以使用双指针法了。
我的解法：哈希表308测试用例超时
超时了...虽然在pycharm里能跑出结果也挺快的
思路是将i和j对应的数的和存到哈希表里，然后用两数之和的方法在哈希表里找0-k。
存在几个问题：
1.i和j不能重复——创造哈希表时就限制j的范围
2.k和另外两个数不能重复——查询时添加判断条件
3.对于哈希表，存在两个数的和相同，但是i和j下标不同的情况，但是字典的key是不能重复的（感觉应该用链表，等我学了链表再想一遍），所以将不同的情况，加载同一个key下面，组成二维数组，就像[[1,2,3,4][2,3,4,5]]这样。k查询的时候还要遍历一遍二维数组的行数
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
# 哈希表，key是i+j，value是i和j的数值及i和j的下标
# 存在key相同，value不同的情况，所以将value组成数组
Hash_Table = dict()
# res = set()
res = []
# for i in range(len(nums)):
# # j 的起始确保i和j下标不重复
# for j in range(i + 1, len(nums)):
# Hash_Table[nums[i] + nums[j]] = [nums[i], nums[j], i, j]
# for k in range(len(nums)):
# if 0 - nums[k] in Hash_Table:
# if k != Hash_Table[0 - nums[k]][2] and k != Hash_Table[0 - nums[k]][3]:
# # 将列表添加到set会报错！！！
# # res.add([Hash_Table[0 - nums[k]][0], Hash_Table[0 - nums[k]][1], nums[k]])
# l1 = [Hash_Table[0 - nums[k]][0], Hash_Table[0 - nums[k]][1], nums[k]]
# l1.sort()
# if l1 not in res:
# res.append(l1)
for i in range(len(nums)):
# j 的起始确保i和j下标不重复
for j in range(i + 1, len(nums)):
if Hash_Table.get(nums[i] + nums[j]):
l2 = Hash_Table.get(nums[i] + nums[j])
l2.append([nums[i], nums[j], i, j])
Hash_Table[nums[i] + nums[j]] = l2
else:
Hash_Table[nums[i] + nums[j]] = [[nums[i], nums[j], i, j]]
for k in range(len(nums)):
if 0 - nums[k] in Hash_Table:
for n in range(len(Hash_Table[0 - nums[k]])):
if k != Hash_Table[0 - nums[k]][n][2] and k != Hash_Table[0 - nums[k]][n][3]:
# 将列表添加到set会报错！！！
# res.add([Hash_Table[0 - nums[k]][0], Hash_Table[0 - nums[k]][1], nums[k]])
l1 = [Hash_Table[0 - nums[k]][n][0], Hash_Table[0 - nums[k]][n][1], nums[k]]
l1.sort()
# 去重
if l1 not in res:
res.append(l1)
return res
☆☆☆题解：双指针法
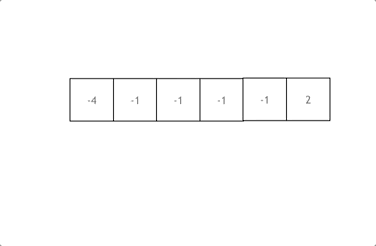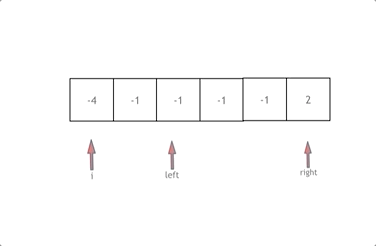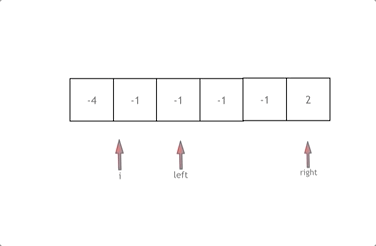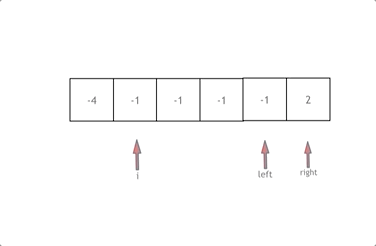
1.数组排序
2.有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。
3.如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。
时间复杂度：O(n^2)，空间复杂度: O(1)
不能有重复的三元组，但三元组内的元素是可以重复的！——
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
result = []
nums.sort()
for i in range(len(nums)):
# 如果第一个元素已经大于0，不需要进一步检查
if nums[i] > 0:
return result
# 跳过相同的元素以避免重复
if i > 0 and nums[i] == nums[i - 1]:
continue
left = i + 1
right = len(nums) - 1
while right > left:
sum_ = nums[i] + nums[left] + nums[right]
if sum_ < 0:
left += 1
elif sum_ > 0:
right -= 1
else:
result.append([nums[i], nums[left], nums[right]])
# 跳过相同的元素以避免重复
while right > left and nums[right] == nums[right - 1]:
right -= 1
while right > left and nums[left] == nums[left + 1]:
left += 1
right -= 1
left += 1
return result题解2：使用字典
1.for循环遍历a
2.对剩下两个数b和c使用字典哈希表：类似于两数之和的方法，然后在哈希表中里找c=0-a-b，没找到就把现在的这个数b存到哈希表，找到了就添加结果，并且在哈希表中删除c，避免结果重复
b和c的去重没明白（感觉不如我的字典好懂...但我的会超时）
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
result = []
nums.sort()
# 找出a + b + c = 0
# a = nums[i], b = nums[j], c = -(a + b)
for i in range(len(nums)):
# 排序之后如果第一个元素已经大于零，那么不可能凑成三元组
if nums[i] > 0:
break
if i > 0 and nums[i] == nums[i - 1]: #三元组元素a去重
continue
d = {}
for j in range(i + 1, len(nums)):
# ？不懂
# c只能从a和b之间取（在当前a下，已经遍历过且存入哈希表的b），假如abbb，则情况只有abb一种，第三个b不会出现新的可能！（中间的b实际上是c）
if j > i + 2 and nums[j] == nums[j-1] == nums[j-2]: # 三元组元素b去重
continue
c = 0 - (nums[i] + nums[j])
if c in d:
result.append([nums[i], nums[j], c])
# 同一个a下，c一样的话，b一定一样，这就会重复，所以找到第一组a，b，c后，把哈希表的c删除，就不会出现第二组了
# c只能从ab之间取。，如果c不删除，后面再找到一个相同的b会和这个c再次匹配
d.pop(c) # 三元组元素c去重
else:
d[nums[j]] = j
return result因为去重没看懂，所以改成了下面这样，但311测试用例超时...
看来两个for循环里的sort耗时很严重
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
result = []
nums.sort()
# 找出a + b + c = 0
# a = nums[i], b = nums[j], c = -(a + b)
for i in range(len(nums)):
# 排序之后如果第一个元素已经大于零，那么不可能凑成三元组
if nums[i] > 0:
break
if i > 0 and nums[i] == nums[i - 1]: #三元组元素a去重
continue
d = {}
for j in range(i + 1, len(nums)):
# if j > i + 2 and nums[j] == nums[j-1] == nums[j-2]: #三元组元素b去重
# continue
c = 0 - (nums[i] + nums[j])
if c in d:
l1 = [nums[i], nums[j], c]
l1.sort()
# 去重
if l1 not in result:
result.append(l1)
# result.append([nums[i], nums[j], c])
# d.pop(c) # 三元组元素c去重
else:
d[nums[j]] = j
return result18 四数之和
我的解法：两层for+双指针...1用例超时...
在三数之和的基础上又嵌一层循环
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
res = []
nums.sort()
for a in range(len(nums)):
if a > 0 and nums[a] == nums[a-1]:# a去重！！！
continue
for b in range(a + 1, len(nums)):
if b - 1 > a and nums[b] == nums[b - 1]:
continue
c = b + 1
d = len(nums) - 1
while c < d:
if c - 1 > b and nums[c] == nums[c - 1]:
c += 1
continue
if d + 1 < len(nums) and nums[d] == nums[d + 1]:
d -= 1
continue
Sum = nums[a] + nums[b] + nums[c] + nums[d]
if Sum == target:
res.append([nums[a], nums[b], nums[c], nums[d]])
c += 1
d -= 1
elif Sum > target:
d -= 1
elif Sum < target:
c += 1
return res☆☆☆题解：双指针
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。
那么一样的道理，五数之和、六数之和等等都采用这种解法。
注意这两个剪枝！！！
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums.sort()
n = len(nums)
result = []
for i in range(n):
if nums[i] > target and nums[i] > 0 and target > 0:# 剪枝（可省）
break
if i > 0 and nums[i] == nums[i-1]:# 去重
continue
for j in range(i+1, n):
if nums[i] + nums[j] > target and target > 0: #剪枝（可省）
break
if j > i+1 and nums[j] == nums[j-1]: # 去重
continue
left, right = j+1, n-1
while left < right:
s = nums[i] + nums[j] + nums[left] + nums[right]
if s == target:
result.append([nums[i], nums[j], nums[left], nums[right]])
while left < right and nums[left] == nums[left+1]:
left += 1
while left < right and nums[right] == nums[right-1]:
right -= 1
left += 1
right -= 1
elif s < target:
left += 1
else:
right -= 1
return result
题解2：字典
class Solution(object):
def fourSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[List[int]]
"""
# 创建一个字典来存储输入列表中每个数字的频率
freq = {}
for num in nums:
freq[num] = freq.get(num, 0) + 1
# 创建一个集合来存储最终答案，并遍历4个数字的所有唯一组合
ans = set()
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
for k in range(j + 1, len(nums)):
val = target - (nums[i] + nums[j] + nums[k])
if val in freq:
# 确保没有重复
# 记录这对数组中有几个重复数字（都等于val）
count = (nums[i] == val) + (nums[j] == val) + (nums[k] == val)
# eg：[2,2,2,2,2]，freq[val]=5代表有五个重复的2，但是选出的答案只需要4个，说明第四个val的下标与前三个下标是可以不冲突的
if freq[val] > count:
# 集合相同答案只加入了一次
ans.add(tuple(sorted([nums[i], nums[j], nums[k], val])))
return [list(x) for x in ans]
4 字符串
tips：
1.先整体反转再局部反转，实现了反转字符串里的单词。
2.反转字符串——达到左旋的效果。
344 反转字符串
☆☆☆我的题解：双指针交换
reverse()也可以，但是这不就没刷题的意义了
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
# s.reverse()
i, j = 0, len(s) - 1
while i < j:
s[i], s[j] = s[j], s[i]
i += 1
j -= 1题解：reversed()
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
s[:] = reversed(s)
题解2：range
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
n = len(s)
for i in range(n // 2):
s[i], s[n - i - 1] = s[n - i - 1], s[i]
题解3：切片
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
s[:] = s[::-1]
题解4：列表推导式
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
s[:] = [s[i] for i in range(len(s) - 1, -1, -1)]
题解5：栈
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
stack = []
for char in s:
stack.append(char)
for i in range(len(s)):
s[i] = stack.pop()
541 反转字符串II
我的题解：
class Solution:
def reverseStr(self, s: str, k: int) -> str:
i = 0
s = list(s)
while len(s) - i >= 2 * k:
for j in range(k // 2):
s[i + j], s[i + k - 1 - j] = s[i + k - 1 - j], s[i + j]
i += 2*k
if len(s) - i >= k:
for j in range(k // 2):
s[i + j], s[i + k - 1 - j] = s[i + k - 1 - j], s[i + j]
else:
for j in range((len(s) - i) // 2):
s[i + j], s[len(s) - 1 - j] = s[len(s) - 1 - j], s[i + j]
s = ''.join(s)
return s题解：切片
class Solution:
def reverseStr(self, s: str, k: int) -> str:
# Two pointers. Another is inside the loop.
p = 0
while p < len(s):
p2 = p + k
# Written in this could be more pythonic.
# 第一次将第一组反转，其余保持不变存过来，
# 第二次在第一次的结果s上，对第二组区间反转，区间前后保持不变存过来，以此类推
# 最后一组p2+k超过下标边界怎么办？
# 在pycharm试了一下，超出边界会当做-1处理，即剩下的全部切片（注意p2一定是大于等于p的）
s = s[:p] + s[p: p2][::-1] + s[p2:]
p = p + 2 * k
return s☆☆☆题解2：
class Solution:
def reverseStr(self, s: str, k: int) -> str:
"""
1. 使用range(start, end, step)来确定需要调换的初始位置
2. 对于字符串s = 'abc'，如果使用s[0:999] ===> 'abc'。字符串末尾如果超过最大长度，则会返回至字符串最后一个值，这个特性可以避免一些边界条件的处理。
3. 用切片整体替换，而不是一个个替换.
"""
def reverse_substring(text):
left, right = 0, len(text) - 1
while left < right:
text[left], text[right] = text[right], text[left]
left += 1
right -= 1
return text
res = list(s)
for cur in range(0, len(s), 2 * k):
res[cur: cur + k] = reverse_substring(res[cur: cur + k])
return ''.join(res)
卡码网54 替换数字
☆☆☆我的题解：ascii码
class Solution:
def change(self,s):
s = list(s)
for i in range(len(s)):
# 计算ascii码
if ord(s[i]) - ord('0') >= 0 and ord(s[i]) - ord('0') <= 9:
s[i] = "number"
return ''.join(s)题解：isdigit()
class Solution:
def change(self, s):
lst = list(s) # Python里面的string也是不可改的，所以也是需要额外空间的。空间复杂度：O(n)。
for i in range(len(lst)):
if lst[i].isdigit():
lst[i] = "number"
return ''.join(lst)
151 翻转字符串里的单词
我的题解：split+反转
多此一举的重新定义lstr，不如题解的join
class Solution:
def reverseWords(self, s: str) -> str:
s = s.split()
for i in range(len(s) // 2):
s[i], s[len(s) - 1 - i] = s[len(s) - 1 - i], s[i]
str = s[0]
for i in range(1, len(s)):
str += ' '
str += s[i]
return str题解：split+反转+join
class Solution:
def reverseWords(self, s: str) -> str:
# 将字符串拆分为单词，即转换成列表类型
words = s.split()
# 反转单词
left, right = 0, len(words) - 1
while left < right:
words[left], words[right] = words[right], words[left]
left += 1
right -= 1
# 将列表转换成字符串
# 用空格分割！！！！！
return " ".join(words)
☆☆☆题解2：删除空白——全部反转——反转单词
先删除空白，然后整个反转，最后单词反转。 因为字符串是不可变类型，所以反转单词的时候，需要将其转换成列表，然后通过join函数再将其转换成列表，所以空间复杂度不是O(1)
class Solution:
def reverseWords(self, s: str) -> str:
# 删除前后空白
s = s.strip()
# 反转整个字符串
s = s[::-1]
# 将字符串拆分为单词，并反转每个单词
s = ' '.join(word[::-1] for word in s.split())
return s题解3：最简洁
class Solution:
def reverseWords(self, s: str) -> str:
return " ".join(reversed(s.split()))卡码网55 右旋字符串
☆☆☆我的题解：切片
#获取输入的数字k和字符串
k = int(input())
s = input()
s = s[-k:]+s[:-k]
print(s)题解：切片
#获取输入的数字k和字符串
k = int(input())
s = input()
#通过切片反转第一段和第二段字符串
#注意：python中字符串是不可变的，所以也需要额外空间
s = s[len(s)-k:] + s[:len(s)-k]
print(s)
28 找出字符串中第一个匹配项的下标
KMP
KMP的经典思想就是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免回退（从头再去做匹配）。
- 即主串指针永远向前移动，回退子串。
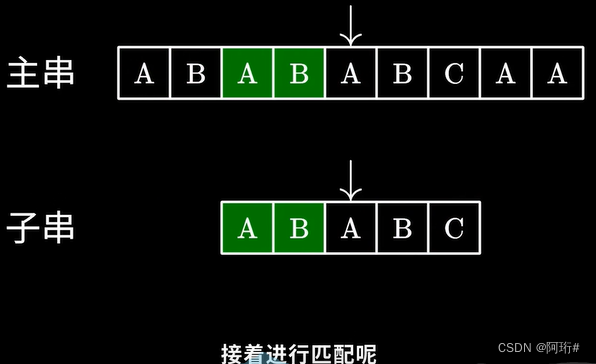
将子串指针从C回退到A，跳过了前面的AB
- 应该跳过多少个字符呢？——next数组
KMP算法在匹配失败时，会在最后一个匹配的字符所对应的next值
这里的2代表子串中我们可以“跳过匹配”的字符个数，即前面的这个AB不需要看了，直接从下一个字符接着匹配，继续测试后面的字符
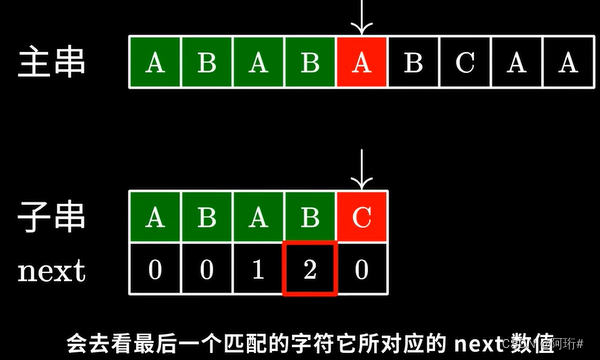
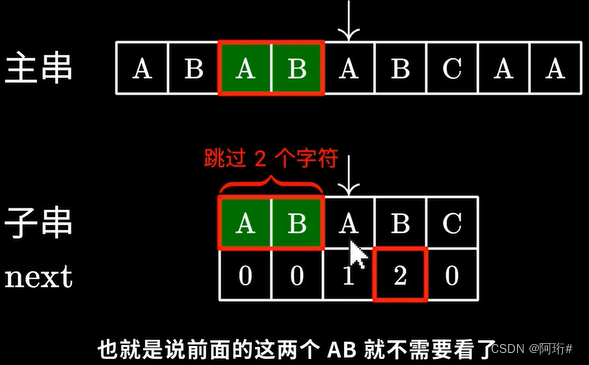
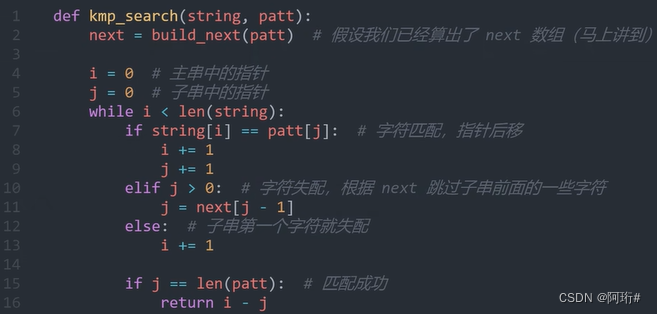
- 程序实现
i永远不递减！
（j>0说明还没回退到子串首元素，可以继续回退子串，j=0还没匹配成功说明要移动主串了）
- next数组的生成
next数值代表在匹配失败时，子串中可以跳过匹配的字符个数
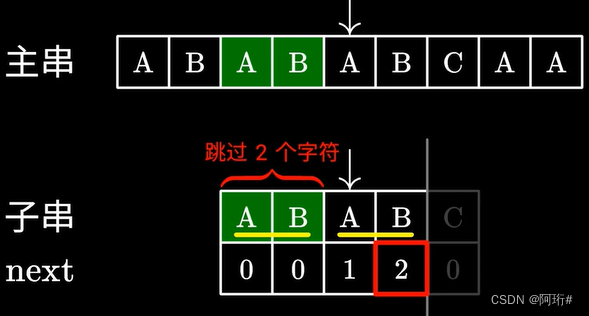
2表示，在ABAB这个子串中，有最长的相等的前缀AB和后缀AB，长度为2.
字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。
简单理解：从前往后数k个字符，从后往前数k个字符，他俩长得一样，这就是相同的前后缀，长度为“k”，我们要找最长的k
前后缀不能是字符串本身
eg：最长的是ABA，长度为3，A也是，但不是最长的
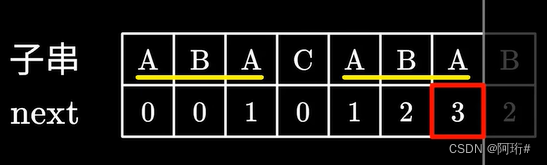
- next数组的计算——递推
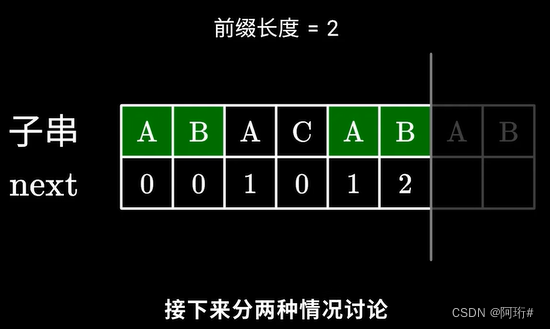已知现在最长相等前后缀是AB，长度为2
1.比较下一个，仍然相等，则前缀+1：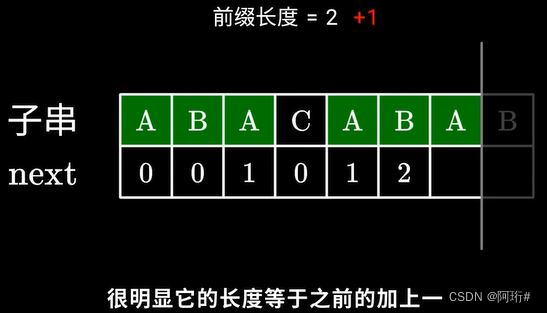
2.下一个不同：
根据前面的情况，我们已知ABAC和ABAB只有最后一个字符不同，即去掉C和B，两个子串ABA，ABA具有完全相同的前后缀，所以相当于把B放到C的位置上计算前后缀，那么已知C的前一个元素A的前后缀是1，所以在1个相同的基础上比较左数第二个元素和B是否相等，相等则前后缀+1，即2
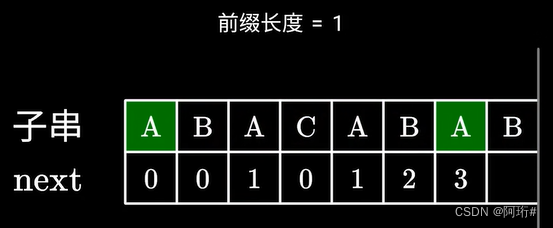
- next数组代码实现
i是当前要计算的元素下标，即指向后缀末尾元素；profix指向前缀末尾长度，表示当前相等前后缀长度
if，当前比较的元素，在之前的基础上，仍然相等，则前缀长度在上一个的基础上+1，赋给当前的i的next数组
else，当前不相等，if，如果此时的前缀长度已经是0了，说明完全没有相同前后缀，所以i的next数为0
else，当前不相等，且前缀长度不为0，那就回退（缩短长度），退到prefix的上一个元素，比较这个元素和i是否相等，若不相等继续退直到相等或长度为0
（即从C不等于B，且C对应的下标profix即前缀长度还不为0，则前缀缩短到C前一位A对应的next=1，即下一次要比较profix=1指向的元素和i指向的元素）
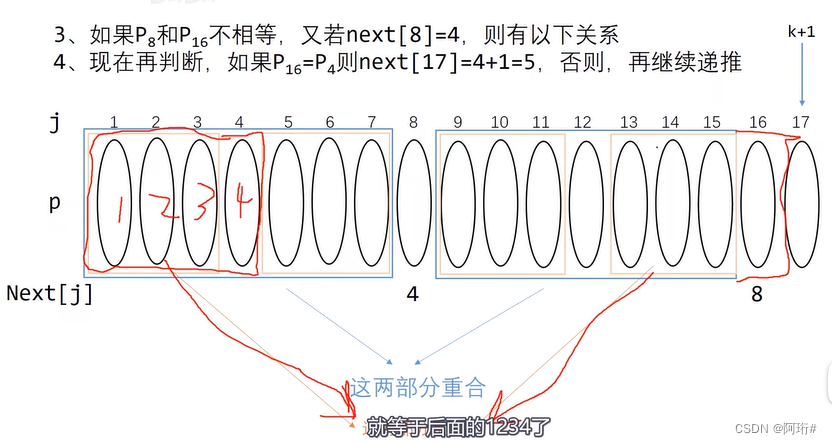
- 为什么要找profix_len-1
看上面的图，已知P16与P8不相等、P1-P7与P9-P15完全相同，想计算P16
就去找P8的前一个P7的next值，比如，P7的next=3，说明P1-P7中，P1-P3和P5-P7是完全相同的，所以加上后面的P9-P11和P13-P15，这四个完全相同，因此我们比较前缀的P4与当前的P16
若P4=P16则P16的next就能在P7的基础上+1。P7等于其他（>0）都同理，能够找到完全相同的四个子串
如果不相等，就继续找P4的的前一位的next，以此类推。
推荐观看：
KMP算法之求next数组代码讲解_哔哩哔哩_bilibili
我的题解：暴力遍历
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
for i in range(len(haystack) - len(needle) + 1):
for j in range(len(needle)):
if haystack[i + j] != needle[j]:
break
if j == len(needle) - 1:
return i
return -1☆☆☆我的题解：学了KMP回来写的
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
self.generate_next(needle)
return self.KMP(haystack, needle)
def KMP(self, s, sub):
i, j = 0, 0 #i是主串指针，j是子串指针
while i < len(s):
if sub[j] == s[i]:
j += 1
i += 1
else:
if j == 0:
i += 1
if j > 0:# 子串回退
j = self.next[j - 1]
if j == len(sub):
return i - j
return -1
def generate_next(self, sub):
nex = [0] * len(sub)
prefix = 0 # 前缀下标
j = 1 # 当前计算的next下标
while j < len(sub):
if sub[prefix] == sub[j]:
prefix += 1
nex[j] = prefix
j += 1
else:
if prefix == 0:
nex[j] = 0
j += 1
else:# 回退
prefix = nex[prefix - 1]
self.next = nex
题解：更简洁的暴力法
class Solution(object):
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
m, n = len(haystack), len(needle)
for i in range(m):
if haystack[i:i+n] == needle:
return i
return -1 题解2：index
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
try:
return haystack.index(needle)
except ValueError:
return -1
题解3：find
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
return haystack.find(needle)
题解4：KMP（next数组不减一）
class Solution:
def getNext(self, next: List[int], s: str) -> None:
j = 0
next[0] = 0
for i in range(1, len(s)):
# 不相等，就一直缩短前缀长度
while j > 0 and s[i] != s[j]:
j = next[j - 1]
# 相等了，在前面的长度基础上+1
if s[i] == s[j]:
j += 1
next[i] = j
def strStr(self, haystack: str, needle: str) -> int:
if len(needle) == 0:
return 0
next = [0] * len(needle)
self.getNext(next, needle)
j = 0
for i in range(len(haystack)):
while j > 0 and haystack[i] != needle[j]:
# 子串根据next数组回退，一直不等就一直回退直到相等或j回到起点
j = next[j - 1]
# 当前匹配上了，j和i都要前移
if haystack[i] == needle[j]:
j += 1
# 全部匹配上了
if j == len(needle):
return i - len(needle) + 1
return -1
459 重复的子字符串
我的题解：KMP+从短到长不断枚举
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
# 若可以，最长的重复子串就是s的一半
# 即，取s的前半段作为子串，检测是否后半段是否一致
# if len(s) < 2:
# return False
# sub = s[:len(s)//2]
# for i in range(len(s)//2):
# if sub[i] != s[i+len(s)//2]:
# return False
# return True # ababab错误
if len(s) < 2:
return False
for i in range(1, len(s) // 2 +1):# i表示子串长度，最小为1，最大为主串的一半
if (len(s) % i) != 0:
continue
self.generate_next(s[:i])
sum_num = 0
for j in range(1,len(s)//i):# 比较次数的范围
flag = self.KMP(s[j*i:(j+1)*i], s[:i])
if flag == -1:#匹配失败
break
sum_num += 1 # 记录比较次数
if sum_num == len(s) // i -1:
return True
return False
def KMP(self, s, sub):
i, j = 0, 0 #i是主串指针，j是子串指针
while i < len(s):
if sub[j] == s[i]:
j += 1
i += 1
else:
if j == 0:
i += 1
if j > 0:# 子串回退
j = self.next[j - 1]
if j == len(sub):
return i - j
return -1
def generate_next(self, sub):
nex = [0] * len(sub)
prefix = 0 # 前缀下标
j = 1 # 当前计算的next下标
while j < len(sub):
if sub[prefix] == sub[j]:
prefix += 1
nex[j] = prefix
j += 1
else:
if prefix == 0:
nex[j] = 0
j += 1
else:# 回退
prefix = nex[prefix - 1]
self.next = nex☆☆☆题解：使用KMP前缀表（next数组不减一）
长度为 n 的字符串 s 是字符串 t=s+s 的子串，并且 s 在 t 中的起始位置不为 0 或 n，当且仅当 s 可以通过由它的一个子串重复多次构成。
- 图解：
当一个字符串s：abcabc，内部由重复的子串组成，那么这个字符串的结构一定是这样的：
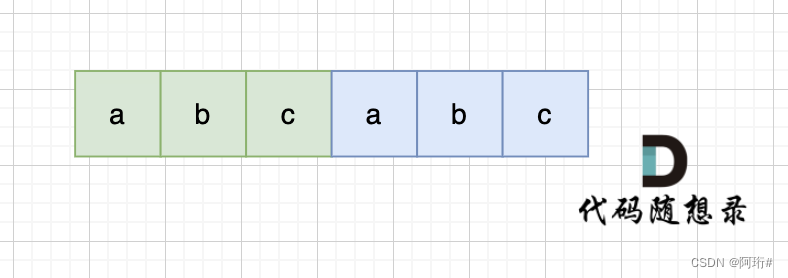也就是由前后相同的子串组成。
那么既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面的子串做前串，前面的子串做后串，就一定还能组成一个s，如图：
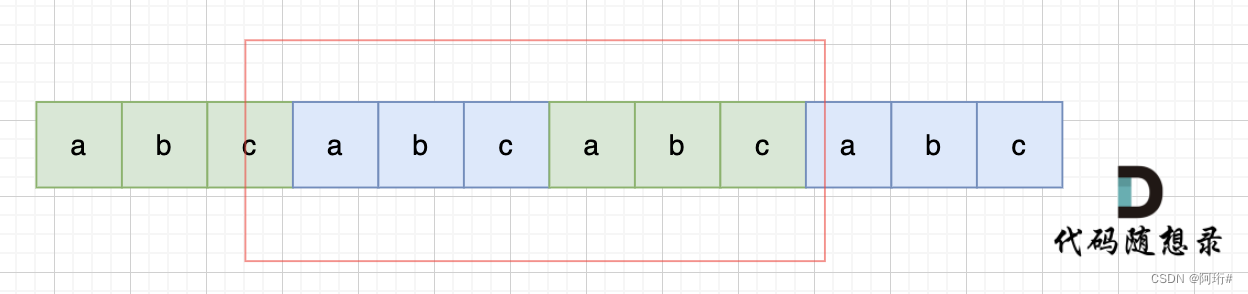
所以判断字符串s是否由重复子串组成，只要两个s拼接在一起，里面还出现一个s的话，就说明是由重复子串组成。
当然，我们在判断 s + s 拼接的字符串里是否出现一个s的的时候，要刨除 s + s 的首字符和尾字符，这样避免在s+s中搜索出原来的s，我们要搜索的是中间拼接出来的s。
- 与KMP的next数组
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串，这里拿字符串s：abababab 来举例，ab就是最小重复单位，如图所示：
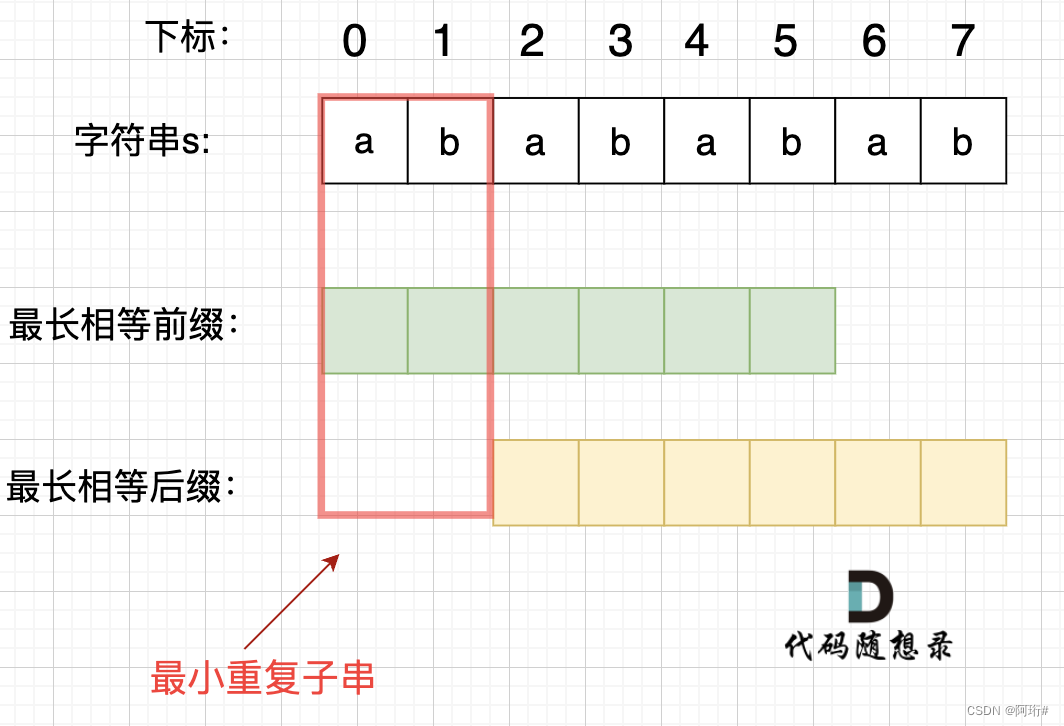
如何找到最小重复子串
这里有同学就问了，为啥一定是开头的ab呢。 其实最关键还是要理解 最长相等前后缀，如图：
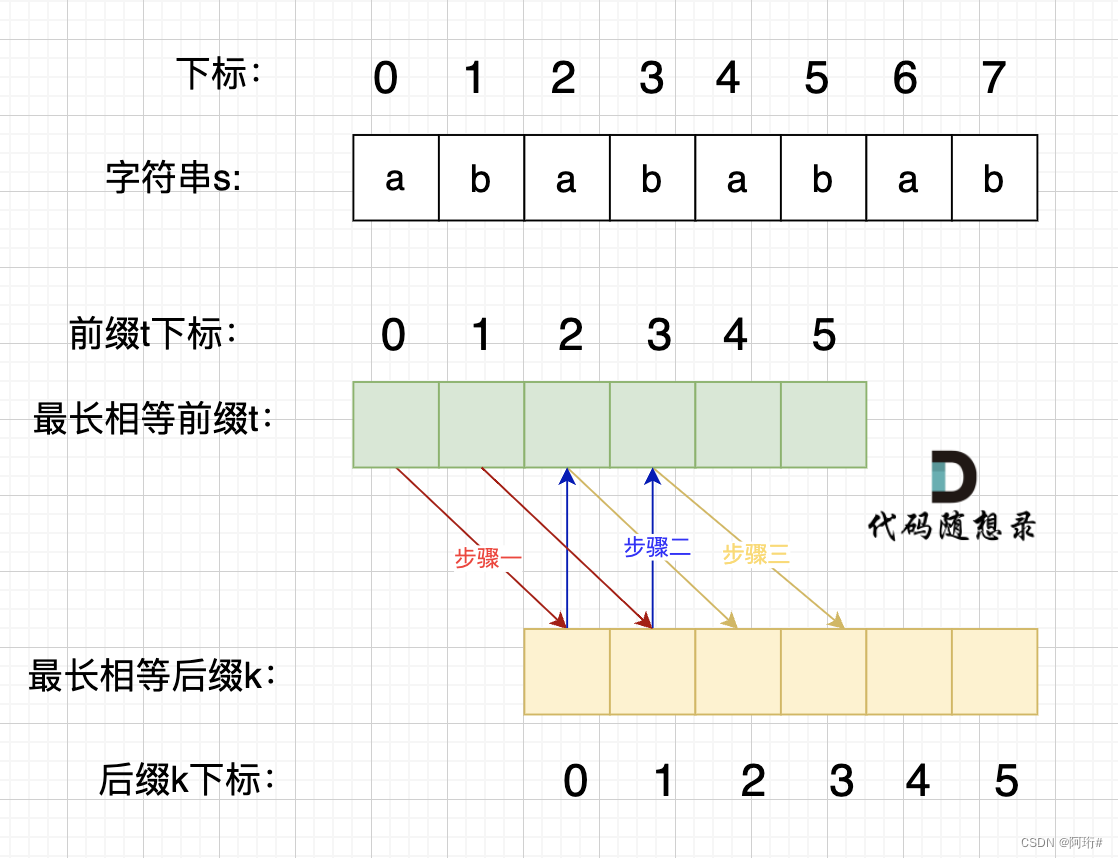
正是因为 最长相等前后缀的规则，当一个字符串由重复子串组成的，最长相等前后缀不包含的子串就是最小重复子串。
- 数学推导：
假设字符串s使用多个重复子串构成（这个子串是最小重复单位），重复出现的子字符串长度是x，所以s是由n * x组成。
因为字符串s的最长相同前后缀的长度一定是不包含s本身，所以 最长相同前后缀长度必然是m * x，而且 n - m = 1，（这里如果不懂，看上面的推理）
所以如果 nx % (n - m)x = 0，就可以判定有重复出现的子字符串。
如果 next[len-1] != 0，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）。
最长相等前后缀的长度为：next[len - 1]。
数组长度为：len。
如果len % (len - (next[len - 1] + 1)) == 0 ，则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ，说明该字符串有重复的子字符串。
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
if len(s) == 0:
return False
nxt = [0] * len(s)
self.getNext(nxt, s)
# next最后一个不为0，即存在最长相等前后缀
# 且数组的长度正好可以被(数组长度-最长相等前后缀的长度) 整除
if nxt[-1] != 0 and len(s) % (len(s) - nxt[-1]) == 0:
return True
return False
# 同KMP的求next
def getNext(self, nxt, s):
nxt[0] = 0
j = 0
for i in range(1, len(s)):
while j > 0 and s[i] != s[j]:
j = nxt[j - 1]
if s[i] == s[j]:
j += 1
nxt[i] = j
return nxt题解2：find
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
n = len(s)
if n <= 1:
return False
ss = s[1:] + s[:-1]
# 即在s+s中去掉首尾找s，找到说明重复，find会返回重复的首元素下标，没找到会返回-1
print(ss.find(s))
return ss.find(s) != -1
题解3：暴力法
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
n = len(s)
if n <= 1:
return False
substr = ""
for i in range(1, n//2 + 1):
if n % i == 0:
substr = s[:i]
if substr * (n//i) == s:
return True
return False
5 栈与队列
- 原理：队列是先进先出，栈是先进后出。
- 栈的实现（先进后出）：list、collections.deque、queue.LifoQueue、链表
Python 栈实现的几种方式及优劣详解_python_脚本之家 Python数据结构之栈详解_python_脚本之家
- 队列的实现（先进先出）：queue.Queue、链表、list
- 双向队列（两端都可进出）：collections.deque、双向链表、list
tips：
1.匹配问题——栈
2.递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。
栈溢出，系统输出的异常是Segmentation fault（当然不是所有的Segmentation fault 都是栈溢出导致的） ，如果你使用了递归，就要想一想是不是无限递归了，那么系统调用栈就会溢出。
而且在企业项目开发中，尽量不要使用递归！在项目比较大的时候，由于参数多，全局变量等等，使用递归很容易判断不充分return的条件，非常容易无限递归（或者递归层级过深），造成栈溢出错误（这种问题还不好排查！）
232 用栈实现队列
我的题解：两个list
class MyQueue:
def __init__(self):
self.l1 = []
self.l2 = []
def push(self, x: int) -> None:
self.l1.append(x)
def pop(self) -> int:
if len(self.l2) == 0:
while len(self.l1) !=0:
self.l2.append(self.l1.pop())
return self.l2.pop()
def peek(self) -> int:
if len(self.l2) == 0:
while len(self.l1) !=0:
self.l2.append(self.l1.pop())
return self.l2[-1]
def empty(self) -> bool:
return True if len(self.l1) == 0 and len(self.l2) == 0 else False
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()☆☆☆题解：pop和peek的代码复用
class MyQueue:
def __init__(self):
"""
in主要负责push，out主要负责pop
"""
self.stack_in = []
self.stack_out = []
def push(self, x: int) -> None:
"""
有新元素进来，就往in里面push
"""
self.stack_in.append(x)
def pop(self) -> int:
"""
Removes the element from in front of queue and returns that element.
"""
if self.empty():
return None
if self.stack_out:
return self.stack_out.pop()
else:
for i in range(len(self.stack_in)):
self.stack_out.append(self.stack_in.pop())
return self.stack_out.pop()
def peek(self) -> int:
"""
Get the front element.
"""
ans = self.pop()
self.stack_out.append(ans)
return ans
def empty(self) -> bool:
"""
只要in或者out有元素，说明队列不为空
"""
return not (self.stack_in or self.stack_out)
225 用队列实现栈
我的解法：两个队列list
pop的时候除了最后一个都出队到q2，找到最后一个之后，再从q2移回去
class MyStack:
def __init__(self):
self.q1 = []# 数据永远保存在q1
self.q2 = []
def push(self, x: int) -> None:
self.q1.append(x)
def pop(self) -> int:
while len(self.q1) > 1:
self.q2.append(self.q1.pop(0))
res = self.q1.pop()
while len(self.q2) > 0:
self.q1.append(self.q2.pop(0))
return res
def top(self) -> int:
res = self.pop()
self.q1.append(res)
return res
def empty(self) -> bool:
return True if len(self.q1) == 0 else False
# Your MyStack object will be instantiated and called as such:
# obj = MyStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.empty()题解1：两个队列deque交换作用
这个解法交换了，更巧妙，避免了移回去的时间复杂度
from collections import deque
class MyStack:
def __init__(self):
"""
Python普通的Queue或SimpleQueue没有类似于peek的功能
也无法用索引访问，在实现top的时候较为困难。
用list可以，但是在使用pop(0)的时候时间复杂度为O(n)
因此这里使用双向队列，我们保证只执行popleft()和append()，因为deque可以用索引访问，可以实现和peek相似的功能
in - 存所有数据
out - 仅在pop的时候会用到
"""
self.queue_in = deque()
self.queue_out = deque()
def push(self, x: int) -> None:
"""
直接append即可
"""
self.queue_in.append(x)
def pop(self) -> int:
"""
1. 首先确认不空
2. 因为队列的特殊性，FIFO，所以我们只有在pop()的时候才会使用queue_out
3. 先把queue_in中的所有元素（除了最后一个），依次出列放进queue_out
4. 交换in和out，此时out里只有一个元素
5. 把out中的pop出来，即是原队列的最后一个
tip：这不能像栈实现队列一样，因为另一个queue也是FIFO，如果执行pop()它不能像
stack一样从另一个pop()，所以干脆in只用来存数据，pop()的时候两个进行交换
"""
if self.empty():
return None
for i in range(len(self.queue_in) - 1):
self.queue_out.append(self.queue_in.popleft())
self.queue_in, self.queue_out = self.queue_out, self.queue_in # 交换in和out，这也是为啥in只用来存
return self.queue_out.popleft()
def top(self) -> int:
"""
写法一：
1. 首先确认不空
2. 我们仅有in会存放数据，所以返回第一个即可（这里实际上用到了栈）
写法二：
1. 首先确认不空
2. 因为队列的特殊性，FIFO，所以我们只有在pop()的时候才会使用queue_out
3. 先把queue_in中的所有元素（除了最后一个），依次出列放进queue_out
4. 交换in和out，此时out里只有一个元素
5. 把out中的pop出来，即是原队列的最后一个，并使用temp变量暂存
6. 把temp追加到queue_in的末尾
"""
# 写法一：
# if self.empty():
# return None
# return self.queue_in[-1] # 这里实际上用到了栈，因为直接获取了queue_in的末尾元素
# 写法二：
if self.empty():
return None
for i in range(len(self.queue_in) - 1):
self.queue_out.append(self.queue_in.popleft())
self.queue_in, self.queue_out = self.queue_out, self.queue_in
temp = self.queue_out.popleft()
self.queue_in.append(temp)
return temp
def empty(self) -> bool:
"""
因为只有in存了数据，只要判断in是不是有数即可
"""
return len(self.queue_in) == 0
☆☆☆题解2：一个队列deque
一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。
class MyStack:
def __init__(self):
self.que = deque()
def push(self, x: int) -> None:
self.que.append(x)
def pop(self) -> int:
if self.empty():
return None
for i in range(len(self.que)-1):
self.que.append(self.que.popleft())
return self.que.popleft()
def top(self) -> int:
# 写法一：
# if self.empty():
# return None
# return self.que[-1]
# 写法二：
if self.empty():
return None
for i in range(len(self.que)-1):
self.que.append(self.que.popleft())
temp = self.que.popleft()
self.que.append(temp)
return temp
def empty(self) -> bool:
return not self.que20 有效括号
我的解法：
class Solution:
def isValid(self, s: str) -> bool:
l1 = []
for i in range(len(s)):
ss = s[i]
if ss == '(' or ss == '{' or ss == '[':
l1.append(ss)
elif ss == ' ':# 处理空格
continue
elif len(l1) == 0:
return False
elif ss == ')' and l1[-1] == '(':
l1.pop()
elif ss == '}' and l1[-1] == '{':
l1.pop()
elif ss == ']' and l1[-1] == '[':
l1.pop()
else:
return False
return True if len(l1) == 0 else False
☆☆☆题解：更巧妙的入栈
# 方法一，仅使用栈，更省空间
class Solution:
def isValid(self, s: str) -> bool:
stack = []
for item in s:
if item == '(':
stack.append(')')
elif item == '[':
stack.append(']')
elif item == '{':
stack.append('}')
elif not stack or stack[-1] != item:
return False
else:
stack.pop()
return True if not stack else False
题解2：字典
# 方法二，使用字典
class Solution:
def isValid(self, s: str) -> bool:
stack = []
mapping = {
'(': ')',
'[': ']',
'{': '}'
}
for item in s:
if item in mapping.keys():
stack.append(mapping[item])
elif not stack or stack[-1] != item: # 不匹配或栈为空
return False
else: # 匹配上了
stack.pop()
return True if not stack else False
1047 删除字符串中的所有相邻重复项
我的解法：栈
class Solution:
def removeDuplicates(self, s: str) -> str:
stack = []
for i in range(len(s)):
if len(stack) == 0:
stack.append(s[i])
elif s[i] == stack[-1]:
stack.pop()
else:
stack.append(s[i])
return ''.join(stack)☆☆☆题解：更简洁的栈
# 方法一，使用栈
class Solution:
def removeDuplicates(self, s: str) -> str:
res = list()
for item in s:
if res and res[-1] == item:
res.pop()
else:
res.append(item)
return "".join(res) # 字符串拼接
题解2：双指针模拟栈
# 方法二，使用双指针模拟栈，如果不让用栈可以作为备选方法。
class Solution:
def removeDuplicates(self, s: str) -> str:
res = list(s)
slow = fast = 0
length = len(res)
while fast < length:
# 如果一样直接换，不一样会把后面的填在slow的位置
res[slow] = res[fast]
# 如果发现和前一个一样，就退一格指针
if slow > 0 and res[slow] == res[slow - 1]:
slow -= 1
else:
slow += 1
fast += 1
return ''.join(res[0: slow])
150 逆波兰表达式求值
如：我们平时写a+b，这是中缀表达式，写成后缀表达式就是：ab+
(a+b)*c-(a+b)/e的后缀表达式为：
(a+b)*c-(a+b)/e
→((a+b)*c)((a+b)/e)-
→((a+b)c*)((a+b)e/)-
→(ab+c*)(ab+e/)-
→ab+c*ab+e/-
我的解法：
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for i in range(len(tokens)):
ss = tokens[i]
if ss == '+' or ss == '-' or ss == '*' or ss == '/':
b = stack.pop()
a = stack.pop()
if ss == '+':
stack.append(a + b)
elif ss == '-':
stack.append(a - b)
elif ss == '*':
stack.append(a * b)
elif ss == '/':# 向下取整
stack.append(int(a / b))
else:
stack.append(int(ss))
return stack.pop()☆☆☆题解：细节上的改进，库实现运算
栈与递归之间在某种程度上是可以转换的！ 其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。
但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了，就可以了。
from operator import add, sub, mul
def div(x, y):
# 使用整数除法的向零取整方式
return int(x / y) if x * y > 0 else -(abs(x) // abs(y))
class Solution(object):
op_map = {'+': add, '-': sub, '*': mul, '/': div}
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for token in tokens:
if token not in {'+', '-', '*', '/'}:
stack.append(int(token))
else:
op2 = stack.pop()
op1 = stack.pop()
stack.append(self.op_map[token](op1, op2)) # 第一个出来的在运算符后面
return stack.pop()
题解2：匿名函数实现运算
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
op_to_binary_fn = {
"+": add,
"-": sub,
"*": mul,
"/": lambda x, y: int(x / y), # 需要注意 python 中负数除法的表现与题目不一致
}
stack = list()
for token in tokens:
try:
num = int(token)
except ValueError:
num2 = stack.pop()
num1 = stack.pop()
num = op_to_binary_fn[token](num1, num2)
finally:
stack.append(num)
return stack[0]239 滑动窗口最大值
我的解法：滑动窗口，比较新加入的元素和当前max
如果max不在区间里就要重新遍历
46/51用例超时了.......
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
MAX = nums[0]
index = 0
res = []
a = 0
for a in range(0, k):
if nums[a] >= MAX:
MAX = nums[a]
index = a
a += 1
res.append(MAX)
i = 1
for j in range(k, len(nums)):
if i > index:
MAX = nums[i]
index = i
for a in range(i, j + 1):
if nums[a] >= MAX:
MAX = nums[a]
index = a
res.append(MAX)
else:
if nums[j] >= MAX:
MAX = nums[j]
index = j
res.append(MAX)
i += 1
return res
☆☆☆题解：单调队列
队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里，窗口移动的时候，队列需要弹出元素。怎么能把窗口要移除的元素（这个元素可不一定是最大值）弹出呢。
其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。
那么这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。
不要以为实现的单调队列就是 对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。
来看一下单调队列如何维护队列里的元素。
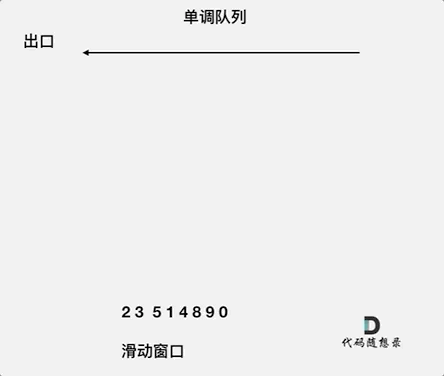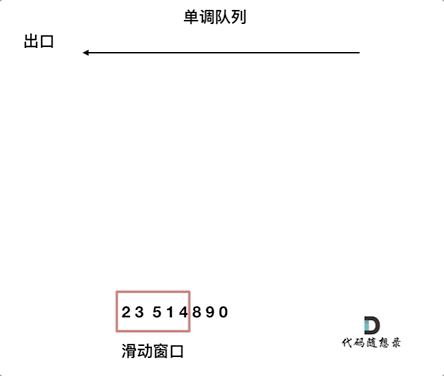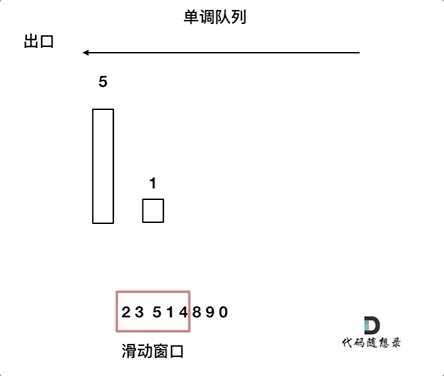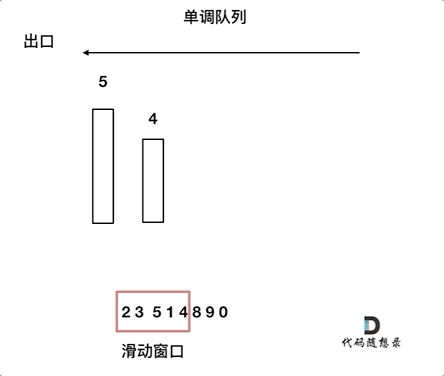
对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢？
设计单调队列的时候，pop，和push操作要保持如下规则：
- pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
- push(value)：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出（注意是从入口处pop，双端队列，eg：5，2，push4，则从右侧pop出2，再push4），直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程，以题目示例为例，输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3，动画如下：
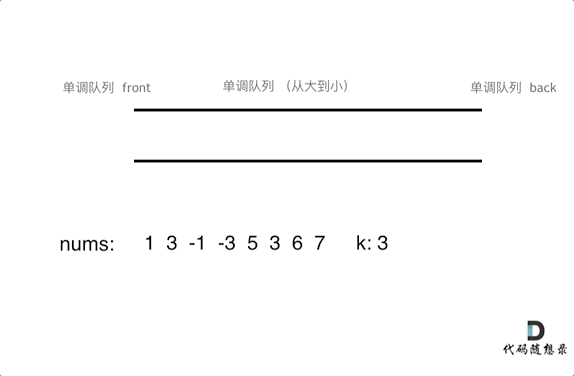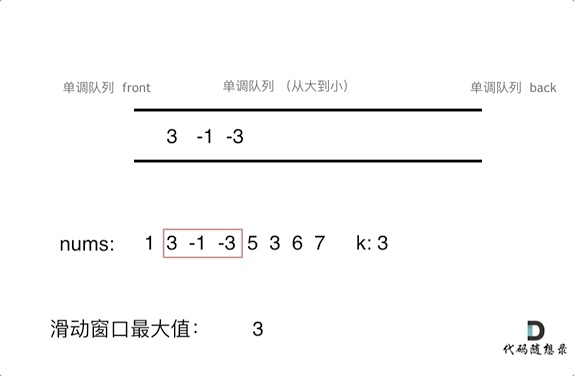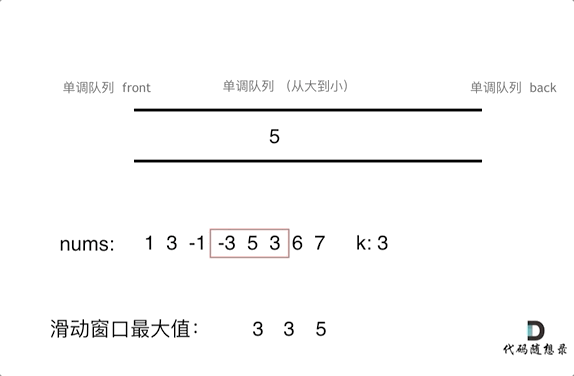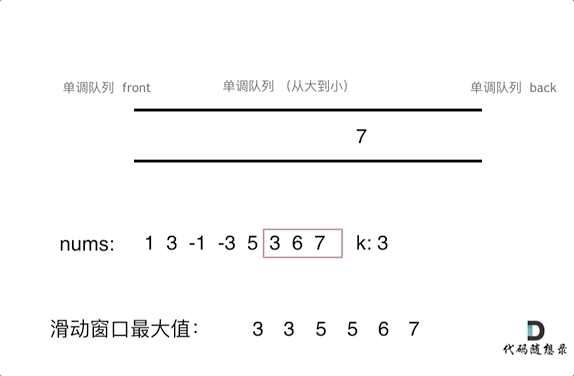
单调队列的实现，nums 中的每个元素最多也就被 push_back 和 pop_back 各一次，没有任何多余操作，所以整体的复杂度还是 O(n)。
空间复杂度因为我们定义一个辅助队列，所以是O(k)。
- 时间复杂度: O(n)
- 空间复杂度: O(k)
tips：
首先要明确的是，题解中单调队列里的pop和push接口，仅适用于本题。单调队列不是一成不变的，而是不同场景不同写法，总之要保证队列里单调递减或递增的原则，所以叫做单调队列。 不要以为本题中的单调队列实现就是固定的写法。
from collections import deque
class MyQueue: #单调队列（从大到小
def __init__(self):
self.queue = deque() #这里需要使用deque实现单调队列，直接使用list会超时
#每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，如果相等则弹出。
#同时pop之前判断队列当前是否为空。
def pop(self, value):
if self.queue and value == self.queue[0]:
self.queue.popleft()#list.pop()时间复杂度为O(n),这里需要使用collections.deque()
#如果push的数值大于入口元素的数值，那么就将队列后端的数值弹出，直到push的数值小于等于队列入口元素的数值为止。
#这样就保持了队列里的数值是单调从大到小的了。
def push(self, value):
while self.queue and value > self.queue[-1]:
self.queue.pop()
self.queue.append(value)
#查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
def front(self):
return self.queue[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
result = []
for i in range(k): #先将前k的元素放进队列
que.push(nums[i])
result.append(que.front()) #result 记录前k的元素的最大值
for i in range(k, len(nums)):
que.pop(nums[i - k]) #滑动窗口移除最前面元素
que.push(nums[i]) #滑动窗口前加入最后面的元素
result.append(que.front()) #记录对应的最大值
return result题解2：优先队列（最大堆）
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
n = len(nums)
# 注意 Python 默认的优先队列是小根堆，所以用-nums[i]
# 所以用-nums[i]
q = [(-nums[i], i) for i in range(k)]
heapq.heapify(q)
# 第一个最大值
ans = [-q[0][0]]
for i in range(k, n):
# 向堆 q中，加入元素(-nums[i], i)
# 建堆用第一个元素-nums[i]为依据进行堆排序
heapq.heappush(q, (-nums[i], i))
# 这个最大值可能并不在滑动窗口中，在这种情况下，这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。
# 不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。
while q[0][1] <= i - k:# max下标位于区间外（小于区间左端点）
heapq.heappop(q)# 移除堆顶元素（移除优先队列的第一位）
ans.append(-q[0][0])
return ans☆☆☆题解3：分块+预处理
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
n = len(nums)
prefixMax, suffixMax = [0] * n, [0] * n
for i in range(n):
if i % k == 0:
prefixMax[i] = nums[i]
else:
prefixMax[i] = max(prefixMax[i - 1], nums[i])
for i in range(n - 1, -1, -1):
if i == n - 1 or (i + 1) % k == 0:
suffixMax[i] = nums[i]
else:
suffixMax[i] = max(suffixMax[i + 1], nums[i])
ans = [max(suffixMax[i], prefixMax[i + k - 1]) for i in range(n - k + 1)]
return ans347 前k个高频元素
我的解法：很墨迹的栈（单调队列）
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
num_dic = dict()
for i in range(len(nums)):
if nums[i] in num_dic:
num_dic[nums[i]] += 1
else:
num_dic[nums[i]] = 1
res_num, temp, res_count, temp_count = [], [], [], []
for number, count in num_dic.items():
if len(res_num) > k and count < res_count[-1]:# 跳过
continue
else:
while len(res_count) > 0 and count > res_count[-1]:
temp.append(res_num.pop())
temp_count.append(res_count.pop())
res_num.append(number)
res_count.append(count)
while temp:
res_num.append(temp.pop())
res_count.append(temp_count.pop())
if len(res_num) > k:
res_num.pop()
res_count.pop()
# if len(res_num) < k:# 加入
# while len(res_count) > 0 and count > res_count[-1]:
# temp.append(res_num.pop())
# temp_count.append(res_count.pop())
# res_num.append(number)
# res_count.append(count)
# while temp:
# res_num.append(temp.pop())
# res_count.append(temp_count.pop())
# else:
# if count < res_count[-1]:# 跳过
# continue
# else:
# while len(res_count) > 0 and count > res_count[-1]:
# temp.append(res_num.pop())
# temp_count.append(res_count.pop())
# res_num.append(number)
# res_count.append(count)
# while temp:
# res_num.append(temp.pop())
# res_count.append(temp_count.pop())
# res_num.pop()
# res_count.pop()
return res_num☆☆☆题解：优先级队列（heapq最小堆）
这道题目主要涉及到如下三块内容：
- 要统计元素出现频率
- 对频率排序
- 找出前K个高频元素
首先统计元素出现的频率，这一类的问题可以使用字典dict来进行统计。
然后是对频率进行排序，这里我们可以使用一种 容器适配器就是优先级队列。
优先级队列：
其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。
堆：
堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。
所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素）
要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。
寻找前k个最大元素流程如图所示：（图中的频率只有三个，所以正好构成一个大小为3的小顶堆，如果频率更多一些，则用这个小顶堆进行扫描）
#时间复杂度：O(nlogk)
#空间复杂度：O(n)
import heapq
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
#要统计元素出现频率
map_ = {} #nums[i]:对应出现的次数
for i in range(len(nums)):
map_[nums[i]] = map_.get(nums[i], 0) + 1
#对频率排序
#定义一个小顶堆，大小为k
pri_que = [] #小顶堆
#用固定大小为k的小顶堆，扫描所有频率的数值
for key, freq in map_.items():
# 建堆使用第一个元素freq排序，也就是频率
heapq.heappush(pri_que, (freq, key))
if len(pri_que) > k: #如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
heapq.heappop(pri_que)
#找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒序来输出到数组
result = [0] * k
for i in range(k-1, -1, -1):
result[i] = heapq.heappop(pri_que)[1]
return result☆☆☆题解2：巧妙的字典
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
# 使用字典统计数字出现次数
time_dict = defaultdict(int)
for num in nums:
time_dict[num] += 1
# 更改字典，key为出现次数，value为相应的数字的集合
index_dict = defaultdict(list)
for key in time_dict:
# 不同数字可能出现相同频率，这时他们串成一个列表当做value，key为频率是唯一的
index_dict[time_dict[key]].append(key)
# 排序
key = list(index_dict.keys())
key.sort()# 默认升序
result = []
cnt = 0
# 获取前k项
while key and cnt != k:
result += index_dict[key[-1]]# 从后往前找最大的
cnt += len(index_dict[key[-1]])# 计算result里加了几个数字了（有可能一个频率加了好几个数进来，所以不能循环k次）
key.pop()
return result[0: k]
6 二叉树
python几种结构的底层实现
字典：哈希表
【python】python中字典的底层是怎么实现的_python底层-CSDN博客
列表：动态数组
集合：哈希表
深入底层了解Python字典和集合，一眼看穿他们的本质！_深入底层了解python字典和集合,一眼看穿他们的本质!-CSDN博客
元组：数组
二叉树的理论基础
二叉树的种类
解题过程中二叉树有两种主要的形式：满二叉树和完全二叉树。
满二叉树
满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。也可以说深度为k，有2^k-1个节点的二叉树。
完全二叉树
完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。
二叉搜索树
前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。
- 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 它的左、右子树也分别为二叉排序树
平衡二叉搜索树
平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。
- 平衡二叉搜索树是不是二叉搜索树和平衡二叉树的结合？
是的，是二叉搜索树和平衡二叉树的结合。
- 平衡二叉树与完全二叉树的区别在于底层节点的位置？
是的，完全二叉树底层必须是从左到右连续的，且次底层是满的。
- 堆是完全二叉树和排序的结合，而不是平衡二叉搜索树？
堆是一棵完全二叉树，同时保证父子节点的顺序关系（有序）。 但完全二叉树一定是平衡二叉树，堆的排序是父节点大于子节点，而搜索树是父节点大于左孩子，小于右孩子，所以堆不是平衡二叉搜索树。
二叉树的存储方式
二叉树可以链式存储，也可以顺序存储。
那么链式存储方式就用指针， 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在各个地址的节点串联一起。
链式存储：
顺序存储：
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。
但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。
二叉树的遍历方式
二叉树主要有两种遍历方式：
- 深度优先遍历：先往深走，遇到叶子节点再往回走。
- 广度优先遍历：一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式
那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：
- 深度优先遍历（DFS）
- 前序遍历（递归法，迭代法）
- 中序遍历（递归法，迭代法）
- 后序遍历（递归法，迭代法）
- 广度优先遍历（BFS）
- 层次遍历（迭代法）
在深度优先遍历中：有三个顺序，前中后序遍历， 有同学总分不清这三个顺序，经常搞混，我这里教大家一个技巧。
这里前中后，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式
- 前序遍历：中左右
- 中序遍历：左中右
- 后序遍历：左右中
实现前中后序遍历，使用递归是比较方便的。
栈其实就是递归的一种实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。
栈与队列的一个应用场景↑
二叉树的定义
链表存储：用类，相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右孩子。
class TreeNode:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right二叉树的递归遍历
每次写递归，都按照这三要素来写
-
确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
-
确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
-
确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
二叉树的迭代遍历
递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。
用栈也可以是实现二叉树的前后中序遍历。
前序遍历（迭代法）
前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。
为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。
动画如下：
中序遍历（迭代法）
刚刚在迭代的过程中，其实我们有两个操作：
- 处理：将元素放进result数组中
- 访问：遍历节点
分析一下为什么刚刚写的前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。
那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。
那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。
动画如下：
后序遍历（迭代法）
再来看后序遍历，先序遍历是中左右，后序遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：
所以后序遍历只需要前序遍历的代码稍作修改就可以了
二叉树的统一迭代
将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。
如何标记呢，就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
动画中，result数组就是最终结果集。
可以看出我们将访问的节点直接加入到栈中，但如果是处理的节点则后面放入一个空节点， 这样只有空节点弹出的时候，才将下一个节点放进结果集。
题目分类大纲：
题目
144 二叉树的前序遍历
☆☆☆我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
self.res = []
self.dfs(root)
return self.res
def dfs(self, node):
if node is None:
return
self.res.append(node.val)
self.dfs(node.left)
self.dfs(node.right)
return我的解法：迭代
注意要判断根节点是否为kong！！！
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
res = []
stack = [root]
while stack:
node = stack.pop()
res.append(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return res☆☆☆我的解法：统一迭代
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
if root:
stack.append(root)
while stack:
cur = stack.pop()
if cur:
if cur.right:
stack.append(cur.right)
if cur.left:
stack.append(cur.left)
stack.append(cur)
stack.append(None)# 在中节点后添加标记
else:
cur = stack.pop()
res.append(cur.val)
return res
145 二叉树的后序遍历
☆☆☆我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
self.res = []
self.dfs(root)
return self.res
def dfs(self, node):
if node is None:
return
self.dfs(node.left)
self.dfs(node.right)
self.res.append(node.val)
return我的解法：迭代
注意相比前序改变左右顺序，然后反转整个数组！！！
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
res = []
stack = [root]
while stack:
node = stack.pop()
res.append(node.val)
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return res[::-1]☆☆☆我的解法：统一迭代
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
if root:
stack.append(root)
while stack:
cur = stack.pop()
if cur:
stack.append(cur)
stack.append(None)
if cur.right:
stack.append(cur.right)
if cur.left:
stack.append(cur.left)
else:
cur = stack.pop()
res.append(cur.val)
return res94 二叉树的中序遍历
☆☆☆我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
self.res = []
self.dfs(root)
return self.res
def dfs(self, node):
if node is None:
return
self.dfs(node.left)
self.res.append(node.val)
self.dfs(node.right)
return我的解法：迭代
访问节点和处理节点不是同时的！！！
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
res = []
stack = []# 不能提前将root结点加入stack中
cur = root
while cur or stack:
if cur:
stack.append(cur)
cur = cur.left
else:
cur = stack.pop()# 当前节点不存在，返回上一节点（pop出一个），中序所以此时append，然后进右分支
res.append(cur.val)
cur = cur.right
return res☆☆☆我的解法 ：统一迭代
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
if root:
stack.append(root)
while stack:
cur = stack.pop()
if cur:
if cur.right:
stack.append(cur.right)
stack.append(cur)
stack.append(None)
if cur.left:
stack.append(cur.left)
else:
cur = stack.pop()
res.append(cur.val)
return res102 二叉树的层序遍历
我的解法：记录节点位置，左儿子x2，右儿子x2+1
这个错误是因为res要添加节点的值cur.val，而不是节点本身cur！！！
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
import math
res, que = [], []
if root:
res.append([])
que.append(root)
que.append(1)# 记序号
n_1 = 0
while que:
cur = que.pop(0)
i = que.pop(0)
n = int(math.log(i,2))# 算在第几行
if n>n_1:# 新的一行重新建列表
res.append([])
n_1 += 1
if cur:
res[n_1].append(cur.val)
if cur.left:
que.append(cur.left)
que.append(2*i)
if cur.right:
que.append(cur.right)
que.append(2*i+1)
return res
看了长度法后自己写了一遍，注意res添加的是节点的val！！！！！！！
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
que = [root]
res = []
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res.append(level)
return res
☆☆☆题解：利用长度法
# 利用长度法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result题解2：递归法
#递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
levels = []
def traverse(node, level):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
traverse(node.left, level + 1)# 第二个参数限制了层数，所以不会影响上一层
traverse(node.right, level + 1)
traverse(root, 0)
return levels107 二叉树的层序遍历II
☆☆☆我的解法：同102，最后反转
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
que = [root]
res = []
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res.append(level)
# res0 = []
# while res:
# res0.append(res.pop())
# return res0
return res[::-1]199 二叉树的右视图
我的解法：同102，只加最后一个
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
que = [root]
res = []
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res.append(level.pop())
return res☆☆☆题解：思路相同但耗时降低、内存占用少
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root:
return []
queue = collections.deque([root])
right_view = []
while queue:
level_size = len(queue)
for i in range(level_size):
node = queue.popleft()
if i == level_size - 1:
right_view.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return right_view题解2：深度优先搜索DFS（栈）
对树进行深度优先搜索，在搜索过程中，我们总是先访问右子树。那么对于每一层来说，我们在这层见到的第一个结点一定是最右边的结点。
6没有右，就找6的左
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict() # 深度为索引，存放节点的值
max_depth = -1
stack = [(root, 0)]
while stack:
node, depth = stack.pop()
if node is not None:
# 维护二叉树的最大深度
max_depth = max(max_depth, depth)
# 如果不存在对应深度的节点我们才插入
rightmost_value_at_depth.setdefault(depth, node.val)
stack.append((node.left, depth + 1))
stack.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]637 二叉树的层平均值
我的解法：同102，sum()/len()
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
if not root:
return []
que = [root]
res = []
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res.append(sum(level)/len(level))
return res☆☆☆题解：思路相同但耗时降低、内存占用少
class Solution:
"""二叉树层平均值迭代解法"""
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
if not root:
return []
queue = collections.deque([root])
averages = []
while queue:
size = len(queue)
level_sum = 0
for i in range(size):
node = queue.popleft()
level_sum += node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
averages.append(level_sum / size)
return averages题解2：深度优先搜索DFS（递归）
使用深度优先搜索计算二叉树的层平均值，需要维护两个数组，counts 用于存储二叉树的每一层的节点数，sums 用于存储二叉树的每一层的节点值之和。搜索过程中需要记录当前节点所在层，如果访问到的节点在第 i 层，则将 counts[i] 的值加 1，并将该节点的值加到 sums[i]。
遍历结束之后，第 i 层的平均值即为 sums[i]/counts[i]。
class Solution:
def averageOfLevels(self, root: TreeNode) -> List[float]:
def dfs(root: TreeNode, level: int):
if not root:
return
if level < len(totals):
totals[level] += root.val
counts[level] += 1
else:
totals.append(root.val)
counts.append(1)
dfs(root.left, level + 1)
dfs(root.right, level + 1)
counts = list()
totals = list()
dfs(root, 0)
return [total / count for total, count in zip(totals, counts)]
429 N叉树的层序遍历
我的解法：同102
注意children是列表，一个一个加
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root:
return []
que = [root]
res = []
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.children:
for i in range(len(cur.children)):
que.append(cur.children[i])
res.append(level)
return res☆☆☆题解：更简洁
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root:
return []
result = []
queue = collections.deque([root])
while queue:
level_size = len(queue)
level = []
for _ in range(level_size):
node = queue.popleft()
level.append(node.val)
for child in node.children:
queue.append(child)
result.append(level)
return result题解2：递归法
# 递归法
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root: return []
result=[]
def traversal(root,depth):
if len(result)==depth:result.append([])
result[depth].append(root.val)
if root.children:
for i in range(len(root.children)):traversal(root.children[i],depth+1)
traversal(root,0)
return result515 在每个树行中找最大值
☆☆☆我的解法：同102，内置max()
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
que = [root]
res = []
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res.append(max(level))
return res题解：不用内置函数找max
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def largestValues(self, root: TreeNode) -> List[int]:
if not root:
return []
result = []
queue = collections.deque([root])
while queue:
level_size = len(queue)
max_val = float('-inf')
for _ in range(level_size):
node = queue.popleft()
max_val = max(max_val, node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
result.append(max_val)
return result题解2：深度优先搜索（递归）
我们用树的「先序遍历」来进行「深度优先搜索」处理，并用 curHeight 来标记遍历到的当前节点的高度。当遍历到 curHeight 高度的节点就判断是否更新该层节点的最大值。
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
ans = []
def dfs(node: TreeNode, curHeight: int) -> None:
if node is None:
return
if curHeight == len(ans):
ans.append(node.val)
else:
ans[curHeight] = max(ans[curHeight], node.val)
dfs(node.left, curHeight + 1)
dfs(node.right, curHeight + 1)
dfs(root, 0)
return ans116 填充每个节点的下一个右侧节点指针
我的解法：
注意root为空时返回root而不是[]
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:
return root
que = [root]
while que:
length = len(que)
for i in range(length):
cur = que.pop(0)
if i == 0:
last = cur
else:
last.next = cur
last = cur
if i == length-1:
cur.next = None
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
return root
☆☆☆题解：更简洁
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
queue = collections.deque([root])
while queue:
level_size = len(queue)
prev = None
for i in range(level_size):
node = queue.popleft()
if prev:
prev.next = node
prev = node
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root题解2：使用已建立的 next 指针
1、从根节点开始，由于第 0 层只有一个节点，所以不需要连接，直接为第 1 层节点建立 next 指针即可。该算法中需要注意的一点是，当我们为第 N 层节点建立 next 指针时，处于第 N−1 层。当第 N 层节点的 next 指针全部建立完成后，移至第 N 层，建立第 N+1 层节点的 next 指针。
2、遍历某一层的节点时，这层节点的 next 指针已经建立。因此我们只需要知道这一层的最左节点，就可以按照链表方式遍历，不需要使用队列。
3、 第一种情况是连接同一个父节点的两个子节点。它们可以通过同一个节点直接访问到，因此执行下面操作即可完成连接。
node.left.next = node.right
第二种情况在不同父亲的子节点之间建立连接，这种情况不能直接连接。
node.right.next = node.next.left
4、完成当前层的连接后，进入下一层重复操作，直到所有的节点全部连接。进入下一层后需要更新最左节点，然后从新的最左节点开始遍历该层所有节点。因为是完美二叉树，因此最左节点一定是当前层最左节点的左孩子。如果当前最左节点的左孩子不存在，说明已经到达该树的最后一层，完成了所有节点的连接。
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
# 从根节点开始
leftmost = root
while leftmost.left:
# 遍历这一层节点组织成的链表，为下一层的节点更新 next 指针
head = leftmost
while head:
# CONNECTION 1
head.left.next = head.right
# CONNECTION 2
if head.next:
head.right.next = head.next.left
# 指针向后移动
head = head.next
# 去下一层的最左的节点
leftmost = leftmost.left
return root 117填充每个节点的下一个右侧节点指针
☆☆☆我的解法：层序遍历，同116完全一样
if not root:
return root
queue = collections.deque([root])
while queue:
level_size = len(queue)
prev = None
for i in range(level_size):
node = queue.popleft()
if prev:
prev.next = node
prev = node
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root题解：使用已建立的 next 指针
- 从根节点开始。因为第 0 层只有一个节点，不需要处理。可以在上一层为下一层建立 next 指针。该方法最重要的一点是：位于第 x 层时为第 x+1 层建立 next 指针。一旦完成这些连接操作，移至第 x+1 层为第 x+2 层建立 next 指针。
- 当遍历到某层节点时，该层节点的 next 指针已经建立。这样就不需要队列从而节省空间。每次只要知道下一层的最左边的节点，就可以从该节点开始，像遍历链表一样遍历该层的所有节点。
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return None
start = root
while start:# last和nextStart每层重置
self.last = None
self.nextStart = None
p = start# 是要给p的下一层建立连接
while p:
if p.left:
self.handle(p.left)
if p.right:
self.handle(p.right)
p = p.next#链表遍历本层
start = self.nextStart# 进入下一层
return root
def handle(self, p):
if self.last:
self.last.next = p
if not self.nextStart:# 当前p是最左端点，准备好下一层的入口
self.nextStart = p
self.last = p104 二叉树的最大深度
☆☆☆我的解法：同102，层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
que = [root]
res = 0
while que:
for _ in range(len(que)):
cur = que.pop(0)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res += 1
return res☆☆☆题解：深度优先搜索，递归
如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为
max(l,r)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
class Solution:
def maxDepth(self, root):
if root is None:
return 0
else:
left_height = self.maxDepth(root.left)
right_height = self.maxDepth(root.right)
return max(left_height, right_height) + 1 111 二叉树的最小深度
☆☆☆我的解法：同102，层序遍历
注意是到叶子结点的距离，叶子结点既没有左儿子也没有右儿子！
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
que = [root]
res = 0
while que:
for _ in range(len(que)):
cur = que.pop(0)
if not cur.left and not cur.right:
return res+1
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res += 1
return res+1☆☆☆题解：深度优先搜索，迭代
首先可以想到使用深度优先搜索的方法，遍历整棵树，记录最小深度。
对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题。
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
if not root.left and not root.right:
return 1
min_depth = 10**9
if root.left:
min_depth = min(self.minDepth(root.left), min_depth)
if root.right:
min_depth = min(self.minDepth(root.right), min_depth)
return min_depth + 1题解2：更简洁的递归
class Solution:
def minDepth(self, root):
if root is None:
return 0
if root.left is None and root.right is not None:
return 1 + self.minDepth(root.right)
if root.left is not None and root.right is None:
return 1 + self.minDepth(root.left)
return 1 + min(self.minDepth(root.left), self.minDepth(root.right))
题解3：前序递归
class Solution:
def __init__(self):
self.result = float('inf')
def getDepth(self, node, depth):
if node is None:
return
if node.left is None and node.right is None:
self.result = min(self.result, depth)
if node.left:
self.getDepth(node.left, depth + 1)
if node.right:
self.getDepth(node.right, depth + 1)
def minDepth(self, root):
if root is None:
return 0
self.getDepth(root, 1)
return self.result226 翻转二叉树
我的解法：深度优先搜索的统一迭代法遍历，前中序都行
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return root
stack = [root]
while stack:
cur = stack.pop()
if cur:
if cur.right:
stack.append(cur.right)
stack.append(cur)
stack.append(None)
if cur.left:
stack.append(cur.left)
else:
cur = stack.pop()
cur.right, cur.left = cur.left, cur.right
return root题解：递归法前序遍历
注：递归法中序不行，因为会把某些节点翻转两次
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root☆☆☆题解2：迭代法前序遍历（更简洁）
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
stack = [root]
while stack:
node = stack.pop()
node.left, node.right = node.right, node.left # 这就是访问操作中节点
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return root题解3：层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
queue = collections.deque([root])
while queue:
for i in range(len(queue)):
node = queue.popleft()
node.left, node.right = node.right, node.left
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
return root 101 对称二叉树
我的解法：层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
que = [root]
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
if cur:
level.append(cur.val)
if cur.left:
que.append(cur.left)
else:
que.append(None)
if cur.right:
que.append(cur.right)
else:
que.append(None)
else:
level.append(None)
n = len(level)
for i in range(n // 2):
if level[i] != level[n-1-i]:
return False
return True
☆☆☆题解：更简洁的层序遍历
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque([root.left, root.right])
while queue:
level_size = len(queue)
if level_size % 2 != 0:
return False
level_vals = []
for i in range(level_size):
node = queue.popleft()
if node:
level_vals.append(node.val)
queue.append(node.left)
queue.append(node.right)
else:
level_vals.append(None)
if level_vals != level_vals[::-1]:
return False
return True
题解2：递归
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
return self.compare(root.left, root.right)
def compare(self, left, right):
#首先排除空节点的情况
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
#排除了空节点，再排除数值不相同的情况
elif left.val != right.val: return False
#此时就是：左右节点都不为空，且数值相同的情况
#此时才做递归，做下一层的判断
outside = self.compare(left.left, right.right) #左子树：左、 右子树：右
inside = self.compare(left.right, right.left) #左子树：右、 右子树：左
isSame = outside and inside #左子树：中、 右子树：中 （逻辑处理）
return isSame☆☆☆题解3：队列，迭代
import collections
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque()
queue.append(root.left) #将左子树头结点加入队列
queue.append(root.right) #将右子树头结点加入队列
while queue: #接下来就要判断这这两个树是否相互翻转
leftNode = queue.popleft()
rightNode = queue.popleft()
if not leftNode and not rightNode: #左节点为空、右节点为空，此时说明是对称的
continue
#左右一个节点不为空，或者都不为空但数值不相同，返回false
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
queue.append(leftNode.left) #加入左节点左孩子
queue.append(rightNode.right) #加入右节点右孩子
queue.append(leftNode.right) #加入左节点右孩子
queue.append(rightNode.left) #加入右节点左孩子
return True
题解4：栈，迭代
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
st = [] #这里改成了栈
st.append(root.left)
st.append(root.right)
while st:
rightNode = st.pop()
leftNode = st.pop()
if not leftNode and not rightNode:
continue
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
st.append(leftNode.left)
st.append(rightNode.right)
st.append(leftNode.right)
st.append(rightNode.left)
return True
100 相同的树
☆☆☆我的解法：队列，迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
que = [p, q]
while que:
leftNode = que.pop(0)
rightNode = que.pop(0)
if not leftNode and not rightNode:
continue
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
que.append(leftNode.left)
que.append(rightNode.left)
que.append(leftNode.right)
que.append(rightNode.right)
return True572 另一棵树的子树
☆☆☆我的解法：
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
que = [root]
while que:
cur = que.pop(0)
flag = self.isSameTree(cur, subRoot)
if flag:
return True
else:
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
return False
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
que = [p, q]
while que:
leftNode = que.pop(0)
rightNode = que.pop(0)
if not leftNode and not rightNode:
continue
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
que.append(leftNode.left)
que.append(rightNode.left)
que.append(leftNode.right)
que.append(rightNode.right)
return True
559 N叉树的最大深度
我的解法：递归
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
depth = []
for child in root.children:
childDepth = self.maxDepth(child)
depth.append(childDepth)
return max(depth) + 1 if depth else 1
☆☆☆题解：更简洁的递归
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
max_depth = 1
for child in root.children:
max_depth = max(max_depth, self.maxDepth(child) + 1)
return max_depth☆☆☆题解2：迭代，队列
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
depth = 0
queue = collections.deque([root])
while queue:
depth += 1
for _ in range(len(queue)):
node = queue.popleft()
for child in node.children:
queue.append(child)
return depth
题解3：迭代，栈
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
max_depth = 0
stack = [(root, 1)]
while stack:
node, depth = stack.pop()
max_depth = max(max_depth, depth)
for child in node.children:
stack.append((child, depth + 1))
return max_depth222 完全二叉树的节点个数
☆☆☆我的解法：层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
que = [root]
count = 0
while que:
for _ in range(len(que)):
cur = que.pop(0)
count += 1
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
return count题解：递归法
class Solution:
def countNodes(self, root: TreeNode) -> int:
return self.getNodesNum(root)
def getNodesNum(self, cur):
if not cur:
return 0
leftNum = self.getNodesNum(cur.left) #左
rightNum = self.getNodesNum(cur.right) #右
treeNum = leftNum + rightNum + 1 #中
return treeNum题解2：更精简的递归法
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
return 1 + self.countNodes(root.left) + self.countNodes(root.right)
题解3：完全二叉树的性质
在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：
在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：
判断其子树是不是满二叉树，如果是则利用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
left = root.left
right = root.right
leftDepth = 0 #这里初始为0是有目的的，为了下面求指数方便
rightDepth = 0
while left: #求左子树深度
left = left.left
leftDepth += 1
while right: #求右子树深度
right = right.right
rightDepth += 1
if leftDepth == rightDepth:
# 右移位操作符 (>>) 将数字的位向右移动指定的位数,每移动一位,相当于将数字除以2。
return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0
return self.countNodes(root.left) + self.countNodes(root.right) + 1
☆☆☆题解4：另一种完全二叉树写法
class Solution: # 利用完全二叉树特性
def countNodes(self, root: TreeNode) -> int:
if not root: return 0
count = 1
left = root.left; right = root.right
while left and right:
count+=1
left = left.left; right = right.right
if not left and not right: # 如果同时到底说明是满二叉树，反之则不是
return 2**count-1
return 1+self.countNodes(root.left)+self.countNodes(root.right) 题解5：另一种完全二叉树写法
class Solution: # 利用完全二叉树特性
def countNodes(self, root: TreeNode) -> int:
if not root: return 0
count = 0
left = root.left; right = root.right
while left and right:
count+=1
left = left.left; right = right.right
if not left and not right: # 如果同时到底说明是满二叉树，反之则不是
return (2<<count)-1
return 1+self.countNodes(root.left)+self.countNodes(root.right) 110 平衡二叉树
我的解法：迭代，215用例出错
未解决
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
stack = [root]
while stack:
cur = stack.pop()
if cur:
#left_height, right_height = 0, 0
if cur.right:
stack.append(cur.right)
right_height = self.maxDepth(cur.right)
if cur.left:
stack.append(cur.right)
left_height = self.maxDepth(cur.left)
if abs(left_height - right_height) > 1:
return False
return True
def maxDepth(self, root):
if not root:
return 0
leftHeight = self.maxDepth(root.left)
rightHeight = self.maxDepth(root.right)
return max(leftHeight, rightHeight) + 1题解：递归法
- 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。
但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：
关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准（毕竟要在这上面刷题）。
因为求深度可以从上到下去查 所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）
既然要求比较高度，必然是要后序遍历。
递归三步曲分析：
1.明确递归函数的参数和返回值
参数：当前传入节点。 返回值：以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢？
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。
2.明确终止条件
递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0
3.明确单层递归的逻辑
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
if self.get_height(root) != -1:
return True
else:
return False
def get_height(self, root: TreeNode) -> int:
# Base Case
if not root:
return 0
# 左
# :=是Python语言中的赋值运算符(主要称为海象运算符),允许在表达式中进行变量赋值。
if (left_height := self.get_height(root.left)) == -1:
return -1
# 右
if (right_height := self.get_height(root.right)) == -1:
return -1
# 中
if abs(left_height - right_height) > 1:
return -1
else:
return 1 + max(left_height, right_height)
☆☆☆题解2：精简递归
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return self.get_hight(root) != -1
def get_hight(self, node):
if not node:
return 0
left = self.get_hight(node.left)
right = self.get_hight(node.right)
if left == -1 or right == -1 or abs(left - right) > 1:
return -1
return max(left, right) + 1
题解3：迭代法
可以使用层序遍历来求深度，但是就不能直接用层序遍历来求高度了，这就体现出求高度和求深度的不同。
本题的迭代方式可以先定义一个函数，专门用来求高度。
这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）
此题用迭代法，其实效率很低，因为没有很好的模拟回溯的过程，所以迭代法有很多重复的计算。
虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。
例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！
因为对于回溯算法已经是非常复杂的递归了，如果再用迭代的话，就是自己给自己找麻烦，效率也并不一定高。
depth怎么算的，加加减减的不还是0吗？？？？？
class Solution:
def getDepth(self, cur):
st = []
if cur is not None:
st.append(cur)
depth = 0
result = 0
while st:
node = st[-1]
if node is not None:
st.pop()
st.append(node) # 中
st.append(None)
depth += 1
if node.right:
st.append(node.right) # 右
if node.left:
st.append(node.left) # 左
else:
node = st.pop()
st.pop()
depth -= 1 #？？？？？？？？？
result = max(result, depth)
return result
def isBalanced(self, root):
st = []
if root is None:
return True
st.append(root)
while st:
node = st.pop() # 中
if abs(self.getDepth(node.left) - self.getDepth(node.right)) > 1:
return False
if node.right:
st.append(node.right) # 右（空节点不入栈）
if node.left:
st.append(node.left) # 左（空节点不入栈）
return True
题解4：精简迭代
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
height_map = {}
stack = [root]
while stack:
node = stack.pop()
if node:
stack.append(node)
stack.append(None)
if node.left: stack.append(node.left)
if node.right: stack.append(node.right)
else:
real_node = stack.pop()
left, right = height_map.get(real_node.left, 0), height_map.get(real_node.right, 0)
if abs(left - right) > 1:
return False
height_map[real_node] = 1 + max(left, right)
return True
257 二叉树的所有路径
我的解法1：迭代，121用例出错，未解决
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
if not root:
return []
stack = [root]
res = []
way = ""
while stack:
cur = stack.pop()
if cur:
if cur.right:
stack.append(cur.right)
stack.append(cur)
stack.append(None)
if cur.left:
stack.append(cur.left)
stack.append(cur)
stack.append(None)
if not cur.left and not cur.right:
stack.append(cur)
stack.append(None)
else:
cur = stack.pop()
way += "->"
way += str(cur.val)
if not cur.left and not cur.right:
res.append(way[2:])
way = ""
return res我的解法2：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
if not root:
return []
self.res = []
self.way = ""
self.findway(root)
return self.res
def findway(self, node):
if not node:
return
self.way += "->"
self.way += str(node.val)
self.findway(node.left)
self.findway(node.right)
if not node.left and not node.right:
self.res.append(self.way[2:])
self.way = self.way[:-(len(str(node.val))+2)]
return☆☆☆题解：递归法+回溯
这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。
在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图：
# Definition for a binary tree node.
class Solution:
def traversal(self, cur, path, result):
path.append(cur.val) # 中
if not cur.left and not cur.right: # 到达叶子节点
sPath = '->'.join(map(str, path))
result.append(sPath)
return
if cur.left: # 左
self.traversal(cur.left, path, result)
path.pop() # 回溯
if cur.right: # 右
self.traversal(cur.right, path, result)
path.pop() # 回溯
def binaryTreePaths(self, root):
result = []
path = []
if not root:
return result
self.traversal(root, path, result)
return result题解2：递归+隐形回溯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from typing import List, Optional
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
if not root:
return []
result = []
self.traversal(root, [], result)
return result
def traversal(self, cur: TreeNode, path: List[int], result: List[str]) -> None:
if not cur:
return
path.append(cur.val)
if not cur.left and not cur.right:
result.append('->'.join(map(str, path)))
if cur.left:
self.traversal(cur.left, path[:], result)# 传了个副本进函数，并不影响外面的path，所以不用在外面回溯了
if cur.right:
self.traversal(cur.right, path[:], result)
题解3：递归+隐形回溯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
path = ''
result = []
if not root: return result
self.traversal(root, path, result)
return result
def traversal(self, cur: TreeNode, path: str, result: List[str]) -> None:
path += str(cur.val)
# 若当前节点为leave，直接输出
if not cur.left and not cur.right:
result.append(path)
if cur.left:
# + '->' 是隐藏回溯
self.traversal(cur.left, path + '->', result)
if cur.right:
self.traversal(cur.right, path + '->', result)
题解4：递归
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
# 题目中节点数至少为1
stack, path_st, result = [root], [str(root.val)], []
while stack:
cur = stack.pop()
path = path_st.pop()
# 如果当前节点为叶子节点，添加路径到结果中
if not (cur.left or cur.right):
result.append(path)
if cur.right:
stack.append(cur.right)
# path_st是一个存了很多地址的列表，每次循环弹出最后一个（一个完整地址），如果是叶子结点，就加入res，不是那弹出来了就不要了，重新加新的地址（连接左右节点的新完整地址）
path_st.append(path + '->' + str(cur.right.val))
if cur.left:
stack.append(cur.left)
path_st.append(path + '->' + str(cur.left.val))
return result404 左叶子之和
我的解法：很笨的递归
注意是左叶子不是左节点之和
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
self.sum = 0
self.dfs(root)
return self.sum
def dfs(self, node):
if node is None:
return
if node.left and not node.left.left and not node.left.right:
self.sum += node.left.val
self.dfs(node.left)
self.dfs(node.right)
return☆☆☆题解：精简递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
leftValue = 0
if root.left is not None and root.left.left is None and root.left.right is None:
leftValue = root.left.val
return leftValue + self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)
题解2：迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
st = [root]
result = 0
while st:
node = st.pop()
if node.left and node.left.left is None and node.left.right is None:
result += node.left.val
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
return result513 找树的左下角的值
☆☆☆我的解法：层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
if not root:
return None
que = [root]
res = None
while que:
level = []
for _ in range(len(que)):
cur = que.pop(0)
level.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
res = level[0]
return res题解：递归+回溯
一直向左遍历到最后一个，它未必是最后一行啊。
我们来分析一下题目：在树的最后一行找到最左边的值。
首先要是最后一行，然后是最左边的值。
如果使用递归法，如何判断是最后一行呢，其实就是深度最大的叶子节点一定是最后一行。
所以要找深度最大的叶子节点。
那么如何找最左边的呢？可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。
class Solution:
def findBottomLeftValue(self, root: TreeNode) -> int:
self.max_depth = float('-inf')
self.result = None
# 设定root节点深度为0
self.traversal(root, 0)
return self.result
def traversal(self, node, depth):
if not node.left and not node.right:
if depth > self.max_depth:
self.max_depth = depth
self.result = node.val
return
if node.left:
depth += 1
self.traversal(node.left, depth)
depth -= 1
if node.right:
depth += 1
self.traversal(node.right, depth)
depth -= 1
题解2：精简递归
class Solution:
def findBottomLeftValue(self, root: TreeNode) -> int:
self.max_depth = float('-inf')
self.result = None
self.traversal(root, 0)
return self.result
def traversal(self, node, depth):
if not node.left and not node.right:
if depth > self.max_depth:
self.max_depth = depth
self.result = node.val
return
if node.left:
self.traversal(node.left, depth+1)
if node.right:
self.traversal(node.right, depth+1)
112 路径总和
☆☆☆我的解法：记路径，递归+回溯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
self.target = targetSum
if not root:
return False
# if not root.left and not root.right and root.val == targetSum:
# return True
if self.traversal(root, []):
return True
else:
return False
def traversal(self, node, path):
path.append(node.val)
if not node.left and not node.right:
if sum(path) == self.target:
return True
return False
if node.left:
if self.traversal(node.left, path):
return True
path.pop()
if node.right:
if self.traversal(node.right, path):
return True
path.pop()
# return False题解：计数器减法，递归回溯
- 确定递归函数的参数和返回类型
参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。
再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：
- 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（113.路径总和ii）
- 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （236）
- 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）
而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？
如图所示：图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。
- 确定终止条件
首先计数器如何统计这一条路径的和呢？
不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
如果遍历到了叶子节点，count不为0，就是没找到。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def traversal(self, cur: TreeNode, count: int) -> bool:
if not cur.left and not cur.right and count == 0: # 遇到叶子节点，并且计数为0
return True
if not cur.left and not cur.right: # 遇到叶子节点直接返回
return False
if cur.left: # 左
count -= cur.left.val
if self.traversal(cur.left, count): # 递归，处理节点
return True
count += cur.left.val # 回溯，撤销处理结果
if cur.right: # 右
count -= cur.right.val
if self.traversal(cur.right, count): # 递归，处理节点
return True
count += cur.right.val # 回溯，撤销处理结果
return False
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if root is None:
return False
return self.traversal(root, sum - root.val) 题解2：精简递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root:
return False
if not root.left and not root.right and sum == root.val:
return True
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
题解3：迭代
如果使用栈模拟递归的话，那么如果做回溯呢？
此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root:
return False
# 此时栈里要放的是pair<节点指针，路径数值>
st = [(root, root.val)]
while st:
node, path_sum = st.pop()
# 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
if not node.left and not node.right and path_sum == sum:
return True
# 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
if node.right:
st.append((node.right, path_sum + node.right.val))
# 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
if node.left:
st.append((node.left, path_sum + node.left.val))
return False
113 路径总和II
☆☆☆我的解法：记路径，递归+回溯，类似112+257
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
self.target = targetSum
res = []
if not root:
return []
self.traversal(root, [], res)
return res
def traversal(self, node, path, res):
path.append(node.val)
if not node.left and not node.right:
if sum(path) == self.target:
# 注意这里用切片[:]，如果直接append(path)，则只会append第一个元素，why？？？
res.append(path[:])
return
if node.left:
self.traversal(node.left, path, res)
path.pop()
if node.right:
self.traversal(node.right, path, res)
path.pop()
# return False题解：计数器减法，递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
result = []
self.traversal(root, targetSum, [], result)
return result
def traversal(self,node, count, path, result):
if not node:
return
path.append(node.val)
count -= node.val
if not node.left and not node.right and count == 0:
# ！！！这里用list()也可以啊
result.append(list(path))
self.traversal(node.left, count, path, result)
self.traversal(node.right, count, path, result)
path.pop()
题解2：迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
if not root:
return []
stack = [(root, [root.val])]
res = []
while stack:
node, path = stack.pop()
if not node.left and not node.right and sum(path) == targetSum:
res.append(path)
if node.right:
# 列表相加合成了新列表
stack.append((node.right, path + [node.right.val]))
if node.left:
stack.append((node.left, path + [node.left.val]))
return res
106 从中序与后序遍历序列构造二叉树
☆☆☆我的解法：递归，pop
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
if not postorder:
return None
val = postorder.pop()
index_i = inorder.index(val)
# 下面两行可以变成root = TreeNode(root_val)
root = TreeNode()
root.val =val
root.left = self.buildTree(inorder[:index_i], postorder[:index_i])
root.right = self.buildTree(inorder[index_i + 1:], postorder[index_i:])
return root题解：差不多的思路，数组切片
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. (递归终止条件)
if not postorder:
return None
# 第二步: 后序遍历的最后一个就是当前的中间节点.
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
postorder_left = postorder[:len(inorder_left)]
postorder_right = postorder[len(inorder_left): len(postorder) - 1]
# 第六步: 递归
root.left = self.buildTree(inorder_left, postorder_left)
root.right = self.buildTree(inorder_right, postorder_right)
# 第七步: 返回答案
return root105 从前序与中序遍历序列构造二叉树
☆☆☆我的解法：递归，pop
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if not preorder:
return None
val = preorder.pop(0)
index_i = inorder.index(val)
root = TreeNode(val)
root.left = self.buildTree(preorder[:index_i], inorder[:index_i])
root.right = self.buildTree(preorder[index_i:], inorder[index_i + 1:])
return root题解：差不多的思路，数组切片
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not preorder:
return None
# 第二步: 前序遍历的第一个就是当前的中间节点.
root_val = preorder[0]
root = TreeNode(root_val)
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割preorder数组. 得到preorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
preorder_left = preorder[1:1 + len(inorder_left)]
preorder_right = preorder[1 + len(inorder_left):]
# 第六步: 递归
root.left = self.buildTree(preorder_left, inorder_left)
root.right = self.buildTree(preorder_right, inorder_right)
# 第七步: 返回答案
return root注：前序和后序不能唯一确定一棵二叉树！！！
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
那么前序和后序可不可以唯一确定一棵二叉树呢？
前序和后序不能唯一确定一棵二叉树！，因为没有中序遍历无法确定左右部分，也就是无法分割。
举一个例子：
tree1 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
tree2 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
那么tree1 和 tree2 的前序和后序完全相同，这是一棵树么，很明显是两棵树！
所以前序和后序不能唯一确定一棵二叉树！
654 最大二叉树
☆☆☆我的解法：切片
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return None
val = max(nums)
index = nums.index(val)
root = TreeNode(val)
root.left = self.constructMaximumBinaryTree(nums[:index])
root.right = self.constructMaximumBinaryTree(nums[index+1:])
return root617 合并二叉树
☆☆☆我的解法：递归 - 前序 - 新建root
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if not root1 and not root2:
return None
if not root1:
return root2
if not root2:
return root1
root = TreeNode(root1.val + root2.val)
root.left = self.mergeTrees(root1.left, root2.left)
root.right = self.mergeTrees(root1.right, root2.right)
return root
题解：递归 - 前序 - 修改root1
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
# 递归终止条件:
# 但凡有一个节点为空, 就立刻返回另外一个. 如果另外一个也为None就直接返回None.
if not root1:
return root2
if not root2:
return root1
# 上面的递归终止条件保证了代码执行到这里root1, root2都非空.
root1.val += root2.val # 中
root1.left = self.mergeTrees(root1.left, root2.left) #左
root1.right = self.mergeTrees(root1.right, root2.right) # 右
return root1 # ⚠️ 注意: 本题我们重复使用了题目给出的节点而不是创建新节点. 节省时间, 空间.
题解2：迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import deque
class Solution:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
if not root1:
return root2
if not root2:
return root1
queue = deque()
queue.append((root1, root2))
while queue:
node1, node2 = queue.popleft()
node1.val += node2.val
if node1.left and node2.left:
queue.append((node1.left, node2.left))
elif not node1.left:
node1.left = node2.left
if node1.right and node2.right:
queue.append((node1.right, node2.right))
elif not node1.right:
node1.right = node2.right
return root1
700 二叉搜索树中的搜索
☆☆☆我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return None
if root.val > val:
return self.searchBST(root.left, val)
elif root.val < val:
return self.searchBST(root.right, val)
else:
return root☆☆☆题解：迭代
二叉搜索树是一个有序树：
- 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 它的左、右子树也分别为二叉搜索树
一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。
对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。
而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。
例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
while root:
if val < root.val: root = root.left
elif val > root.val: root = root.right
else: return root
return None
题解2：栈，遍历
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
stack = [root]
while stack:
node = stack.pop()
# 根据TreeNode的定义
# node携带有三类信息 node.left/node.right/node.val
# 找到val直接返回node 即是找到了该节点为根的子树
# 此处node.left/node.right/val的前后顺序可打乱
if node.val == val:
return node
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return None
98 验证二叉搜索树
我的解法：77用例测试错误
3比5小是错的，未解决
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
if root.left and root.left.val >= root.val:
return False
if root.right and root.right.val <= root.val:
return False
if not self.isValidBST(root.left):
return False
if not self.isValidBST(root.right):
return False
return True题解：递归法，利用中序递增性质，转换成数组
要知道中序遍历下，输出的二叉搜索树节点的数值是有序序列。
有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。
不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。
我们要比较的是 左子树所有节点小于中间节点，右子树所有节点大于中间节点。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.vec = []
def traversal(self, root):
if root is None:
return
self.traversal(root.left)
self.vec.append(root.val) # 将二叉搜索树转换为有序数组
self.traversal(root.right)
def isValidBST(self, root):
self.vec = [] # 清空数组
self.traversal(root)
for i in range(1, len(self.vec)):
# 注意要小于等于，搜索树里不能有相同元素
if self.vec[i] <= self.vec[i - 1]:
return False
return True
题解2：迭代
中序遍历从左下角开始，左中右遍历，整体应该是递增的，因此每次判断当前节点（中）是不是比上一个（作为中的）节点大
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root):
stack = []
cur = root
pre = None # 记录前一个节点
while cur is not None or len(stack) > 0:
if cur is not None:
stack.append(cur)
cur = cur.left # 左
else:
cur = stack.pop() # 中
if pre is not None and cur.val <= pre.val:
return False
pre = cur # 保存前一个访问的结点
cur = cur.right # 右
return True
题解3：递归法，设定极小值，进行比较
从左下开始左中右遍历，每次将遇到的中判断是否比上一个大，符合的话更新当前节点为最小值，然后继续遍历
class Solution:
def __init__(self):
self.maxVal = float('-inf') # 因为后台测试数据中有int最小值
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
# 中序遍历，验证遍历的元素是不是从小到大
if self.maxVal < root.val:
self.maxVal = root.val
else:
return False
right = self.isValidBST(root.right)
return left and right☆☆☆题解4：递归法，和上一个差不多
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.pre = None # 用来记录前一个节点
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
if self.pre is not None and self.pre.val >= root.val:
return False
self.pre = root # 记录前一个节点
right = self.isValidBST(root.right)
return left and right
530 二叉搜索树的最小绝对差
☆☆☆我的解法：递归，中序
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
import sys
self.pre = None
self.MIN = sys.maxsize
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
if not root:
return
self.getMinimumDifference(root.left)
if self.pre:
self.MIN = min(self.MIN, abs(self.pre.val - root.val))
self.pre = root
self.getMinimumDifference(root.right)
return self.MIN
题解：差不多的递归中序
class Solution:
def __init__(self):
self.result = float('inf')
self.pre = None
def traversal(self, cur):
if cur is None:
return
self.traversal(cur.left) # 左
if self.pre is not None: # 中
self.result = min(self.result, cur.val - self.pre.val)
self.pre = cur # 记录前一个
self.traversal(cur.right) # 右
def getMinimumDifference(self, root):
self.traversal(root)
return self.result题解2：递归中序，但数组
class Solution:
def __init__(self):
self.vec = []
def traversal(self, root):
if root is None:
return
self.traversal(root.left)
self.vec.append(root.val) # 将二叉搜索树转换为有序数组
self.traversal(root.right)
def getMinimumDifference(self, root):
self.vec = []
self.traversal(root)
if len(self.vec) < 2:
return 0
result = float('inf')
for i in range(1, len(self.vec)):
# 统计有序数组的最小差值
result = min(result, self.vec[i] - self.vec[i - 1])
return result
题解3：迭代
class Solution:
def getMinimumDifference(self, root):
stack = []
cur = root
pre = None
result = float('inf')
while cur is not None or len(stack) > 0:
if cur is not None:
stack.append(cur) # 将访问的节点放进栈
cur = cur.left # 左
else:
cur = stack.pop()
if pre is not None: # 中
result = min(result, cur.val - pre.val)
pre = cur
cur = cur.right # 右
return result501 二叉搜索树中的众数
我的解法：中序递归，数组，滑动窗口
中序递归变成数组（和之前方法一致），然后使用滑动窗口找众数（滑动窗口的区间不会缩短，只会保持不变或边长）
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.vec = []
def traversal(self, root):
if not root:
return
self.traversal(root.left)
self.vec.append(root.val)
self.traversal(root.right)
def findMode(self, root: Optional[TreeNode]) -> List[int]:
self.vec = []
self.traversal(root)
res = []
if len(self.vec) < 1:
return self.vec
i, j = 0, 0
max_len = 0
while j < len(self.vec):
if self.vec[i] == self.vec[j]:
if j - i + 1 > max_len:
res = [self.vec[i]]
max_len = j - i + 1
elif j - i + 1 == max_len:
res.append(self.vec[i])
j += 1
else:
i, j = j, 2*j-i-1
return res
☆☆☆题解：递归，但用pre记录频次
class Solution:
def __init__(self):
self.maxCount = 0 # 最大频率
self.count = 0 # 统计频率
self.pre = None
self.result = []
def searchBST(self, cur):
if cur is None:
return
self.searchBST(cur.left) # 左
# 中
if self.pre is None: # 第一个节点
self.count = 1
elif self.pre.val == cur.val: # 与前一个节点数值相同
self.count += 1
else: # 与前一个节点数值不同
self.count = 1
self.pre = cur # 更新上一个节点
if self.count == self.maxCount: # 如果与最大值频率相同，放进result中
self.result.append(cur.val)
if self.count > self.maxCount: # 如果计数大于最大值频率
self.maxCount = self.count # 更新最大频率
self.result = [cur.val] # 很关键的一步，不要忘记清空result，之前result里的元素都失效了
self.searchBST(cur.right) # 右
return
def findMode(self, root):
self.count = 0
self.maxCount = 0
self.pre = None # 记录前一个节点
self.result = []
self.searchBST(root)
return self.result题解2：字典统计频率，所有二叉树皆可用这个方法（没有利用二叉搜索树性质）
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import defaultdict
class Solution:
def searchBST(self, cur, freq_map):
if cur is None:
return
freq_map[cur.val] += 1 # 统计元素频率
self.searchBST(cur.left, freq_map)
self.searchBST(cur.right, freq_map)
def findMode(self, root):
freq_map = defaultdict(int) # key:元素，value:出现频率
result = []
if root is None:
return result
self.searchBST(root, freq_map)
max_freq = max(freq_map.values())
for key, freq in freq_map.items():
if freq == max_freq:
result.append(key)
return result
题解3：迭代，思路同题解1
class Solution:
def findMode(self, root):
st = []
cur = root
pre = None
maxCount = 0 # 最大频率
count = 0 # 统计频率
result = []
while cur is not None or st:
if cur is not None: # 指针来访问节点，访问到最底层
st.append(cur) # 将访问的节点放进栈
cur = cur.left # 左
else:
cur = st.pop()
if pre is None: # 第一个节点
count = 1
elif pre.val == cur.val: # 与前一个节点数值相同
count += 1
else: # 与前一个节点数值不同
count = 1
if count == maxCount: # 如果和最大值相同，放进result中
result.append(cur.val)
if count > maxCount: # 如果计数大于最大值频率
maxCount = count # 更新最大频率
result = [cur.val] # 很关键的一步，不要忘记清空result，之前result里的元素都失效了
pre = cur
cur = cur.right # 右
return result236 二叉树的最近公共祖先
我的解法：23错误，未解决
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def __init__(self):
self.father = None
self.pre = None
self.count = 0
self.res = None
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root:
return
if root == p or root == q:
self.count += 1
if self.count == 1:
self.father = self.pre
if self.count == 2:
return
self.pre = root
self.lowestCommonAncestor(root.left, p, q)
self.lowestCommonAncestor(root.right, p, q)
if self.count == 2 and (root == p or root == q):
self.res = root
return self.res if self.res else self.father题解：递归
遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。
那么二叉树如何可以自底向上查找呢？
回溯啊，二叉树回溯的过程就是从低到上。
后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。
接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。
首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。 即情况一：
容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q(p)。 情况二：
其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。
因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本身就是 公共祖先的情况。
这道题要遍历整棵树！！！（不懂为什么？？？）
如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解
如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。
如图：
归纳如下三点：
-
求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。
-
在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
-
要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。
可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。
本题没有给出迭代法，因为迭代法不适合模拟回溯的过程。理解递归的解法就够了。
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root == q or root == p or root is None:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left is not None and right is not None:
return root
if left is None and right is not None:
return right
elif left is not None and right is None:
return left
else:
return None
☆☆☆题解2：精简递归
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root == q or root == p or root is None:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left is not None and right is not None:
return root
if left is None:
return right
return left235 二叉搜索树的最近公共祖先
我的解法：递归，详细分开写的
当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[q, p]区间中，那么cur就是 q和p的最近公共祖先。
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
if not root:
return root
if root.val > p.val and root.val < q.val:
return root
if root.val < p.val and root.val > q.val:
return root
if root.val > p.val and root.val > q.val:
return self.lowestCommonAncestor(root.left, p, q)
if root.val < p.val and root.val < q.val:
return self.lowestCommonAncestor(root.right, p, q)
if root == p or root == q:
return root☆☆☆题解：递归，精简版
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root.val > p.val and root.val > q.val:
return self.lowestCommonAncestor(root.left, p, q)
elif root.val < p.val and root.val < q.val:
return self.lowestCommonAncestor(root.right, p, q)
else:
return root题解2：迭代
class Solution:
def lowestCommonAncestor(self, root, p, q):
while root:
if root.val > p.val and root.val > q.val:
root = root.left
elif root.val < p.val and root.val < q.val:
root = root.right
else:
return root
return None701 二叉搜索树中的插入操作
我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return TreeNode(val)
if root.val > val:
if root.left:
self.insertIntoBST(root.left, val)
else:
root.left = TreeNode(val)
else:
if root.right:
self.insertIntoBST(root.right, val)
else:
root.right = TreeNode(val)
return root☆☆☆题解：更简洁的递归
class Solution:
def insertIntoBST(self, root, val):
if root is None:
node = TreeNode(val)
return node
if root.val > val:
root.left = self.insertIntoBST(root.left, val)
if root.val < val:
root.right = self.insertIntoBST(root.right, val)
return root题解2：迭代
class Solution:
def insertIntoBST(self, root, val):
if root is None: # 如果根节点为空，创建新节点作为根节点并返回
node = TreeNode(val)
return node
cur = root
parent = root # 记录上一个节点，用于连接新节点
while cur is not None:
parent = cur
if cur.val > val:
cur = cur.left
else:
cur = cur.right
node = TreeNode(val)
if val < parent.val:
parent.left = node # 将新节点连接到父节点的左子树
else:
parent.right = node # 将新节点连接到父节点的右子树
return root
450 删除二叉搜索树中的节点
我的解法：递归，删除+插入
有以下五种情况：
- 第一种情况：没找到删除的节点，遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
- 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
- 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
- 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root:
return root
if root.val > key:
root.left = self.deleteNode(root.left, key)
elif root.val < key:
root.right = self.deleteNode(root.right, key)
else:
if not root.left:
return root.right
elif not root.right:
return root.left
else:# 两边都不空，那就把右边提上来，把左边挂在右边的左儿子位置，然后把右边的左儿子重新插入
node = root.right.left
root.right.left = root.left
if node:
self.insertIntoBST(root.right, node)
return root.right
return root
def insertIntoBST(self, root, node):
if root is None:
return node
if root.val > node.val:
root.left = self.insertIntoBST(root.left, node)
if root.val < node.val:
root.right = self.insertIntoBST(root.right, node)
return root
☆☆☆题解：不用插入，递归
class Solution:
def deleteNode(self, root, key):
if root is None:
return root
if root.val == key:
if root.left is None and root.right is None:
return None
elif root.left is None:
return root.right
elif root.right is None:
return root.left
else:
cur = root.right
while cur.left is not None:# 这里的循环一直找到右边的最下的左儿子为空的地方，把原来的左边挂在空的位置上，因为原来的左边的全部都是比右边小的，所以可以不断往左分支走，挂在整棵树的最小位置
cur = cur.left
cur.left = root.left
return root.right
if root.val > key:
root.left = self.deleteNode(root.left, key)
if root.val < key:
root.right = self.deleteNode(root.right, key)
return root题解2：简洁的递归
class Solution:
def deleteNode(self, root, key):
if root is None: # 如果根节点为空，直接返回
return root
if root.val == key: # 找到要删除的节点
if root.right is None: # 如果右子树为空，直接返回左子树作为新的根节点
return root.left
cur = root.right
while cur.left: # 找到右子树中的最左节点
cur = cur.left
root.val, cur.val = cur.val, root.val # 将要删除的节点值与最左节点值交换
root.left = self.deleteNode(root.left, key) # 在左子树中递归删除目标节点
root.right = self.deleteNode(root.right, key) # 在右子树中递归删除目标节点
return root题解3：迭代
class Solution:
def deleteOneNode(self, target: TreeNode) -> TreeNode:
"""
将目标节点（删除节点）的左子树放到目标节点的右子树的最左面节点的左孩子位置上
并返回目标节点右孩子为新的根节点
是动画里模拟的过程
"""
if target is None:
return target
if target.right is None:
return target.left
cur = target.right
while cur.left:
cur = cur.left
cur.left = target.left
return target.right
def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
if root is None:
return root
cur = root
pre = None # 记录cur的父节点，用来删除cur
while cur:
if cur.val == key:
break
pre = cur
if cur.val > key:
cur = cur.left
else:
cur = cur.right
if pre is None: # 如果搜索树只有头结点
return self.deleteOneNode(cur)
# pre 要知道是删左孩子还是右孩子
if pre.left and pre.left.val == key:
pre.left = self.deleteOneNode(cur)
if pre.right and pre.right.val == key:
pre.right = self.deleteOneNode(cur)
return root669 修剪二叉搜索树
☆☆☆我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
if not root:
return root
if root.val <= high and root.val >= low:
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
elif root.val < low:
return self.trimBST(root.right, low, high)
elif root.val > high:
return self.trimBST(root.left, low, high)
return root题解：迭代
class Solution:
def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
if not root:
return None
# 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
while root and (root.val < L or root.val > R):
if root.val < L:
root = root.right # 小于L往右走
else:
root = root.left # 大于R往左走
cur = root
# 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
while cur:
while cur.left and cur.left.val < L:
cur.left = cur.left.right
cur = cur.left
cur = root
# 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
while cur:
while cur.right and cur.right.val > R:
cur.right = cur.right.left
cur = cur.right
return root108 将有序数组转换为二叉搜索树
☆☆☆我的解法：递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if nums:
n = len(nums)
root = TreeNode(nums[n // 2])
root.left = self.sortedArrayToBST(nums[:n // 2])
root.right = self.sortedArrayToBST(nums[n // 2 + 1 : ])
return root
else:
return None题解：递归但不精简
class Solution:
def traversal(self, nums: List[int], left: int, right: int) -> TreeNode:
if left > right:
return None
mid = left + (right - left) // 2
root = TreeNode(nums[mid])
root.left = self.traversal(nums, left, mid - 1)
root.right = self.traversal(nums, mid + 1, right)
return root
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
root = self.traversal(nums, 0, len(nums) - 1)
return root题解2：迭代
from collections import deque
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
if len(nums) == 0:
return None
root = TreeNode(0) # 初始根节点
nodeQue = deque() # 放遍历的节点
leftQue = deque() # 保存左区间下标
rightQue = deque() # 保存右区间下标
nodeQue.append(root) # 根节点入队列
leftQue.append(0) # 0为左区间下标初始位置
rightQue.append(len(nums) - 1) # len(nums) - 1为右区间下标初始位置
while nodeQue:
curNode = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
mid = left + (right - left) // 2
curNode.val = nums[mid] # 将mid对应的元素给中间节点
if left <= mid - 1: # 处理左区间
curNode.left = TreeNode(0)# 还有数能放，这里先初始化一个0的节点，然后再pop出去用数组赋值
nodeQue.append(curNode.left)
leftQue.append(left)
rightQue.append(mid - 1)
if right >= mid + 1: # 处理右区间
curNode.right = TreeNode(0)
nodeQue.append(curNode.right)
leftQue.append(mid + 1)
rightQue.append(right)
return root538 把二叉搜索树转换为累加树
我的解法：递归，记录sum
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.sum = 0
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root :
return
if root.right:
self.convertBST(root.right)
self.sum += root.val
root.val = self.sum
if root.left:
self.convertBST(root.left)
return root☆☆☆题解：递归，记录sum，精简版
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.count = 0
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root == None:
return
'''
倒序累加替换：
'''
# 右
self.convertBST(root.right)
# 中
# 中节点：用当前root的值加上pre的值
self.count += root.val
root.val = self.count
# 左
self.convertBST(root.left)
return root题解2：指针记录前一节点，递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
self.pre = 0 # 记录前一个节点的数值
self.traversal(root)
return root
def traversal(self, cur):
if cur is None:
return
self.traversal(cur.right)
cur.val += self.pre
self.pre = cur.val
self.traversal(cur.left)题解3：迭代
class Solution:
def __init__(self):
self.pre = 0 # 记录前一个节点的数值
def traversal(self, root):
stack = []
cur = root
while cur or stack:
if cur:
stack.append(cur)
cur = cur.right # 右
else:
cur = stack.pop() # 中
cur.val += self.pre
self.pre = cur.val
cur = cur.left # 左
def convertBST(self, root):
self.pre = 0
self.traversal(root)
return root题解4：迭代
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root: return root
stack = []
result = []
cur = root
pre = 0
while cur or stack:
if cur:
stack.append(cur)
cur = cur.right
else:
cur = stack.pop()
cur.val+= pre
pre = cur.val
cur =cur.left
return root7 回溯算法
回溯法，一般可以解决如下几种问题：
- 组合问题：N个数里面按一定规则找出k个数的集合
- 切割问题：一个字符串按一定规则有几种切割方式
- 子集问题：一个N个数的集合里有多少符合条件的子集
- 排列问题：N个数按一定规则全排列，有几种排列方式
- 棋盘问题：N皇后，解数独等等
组合是不强调元素顺序的，排列是强调元素顺序。
所有回溯法的问题都可以抽象为树形结构！
因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。
递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。
回溯算法模板（C++）
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表); // 递归
回溯，撤销处理结果
}
}
77 组合
我的解法：回溯
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
self.result = []
li = []
for i in range(n):
li.append(i + 1)
if n == k:
return [li]
self.select(li, k, [])
return self.result
def select(self, li, k, res):
if k <= 0:
# 因为前面避免了重复，所以这里直接加进去，否则还要再用sorted()来避免重复
self.result.append(res[:])# 注意用切片复制进去，否则相当于把res加进去，后续res改变这个里面的也会变
return self.result
num = len(li)
for j in range(num):
res.append(li[j])
# j影响：li这个区间每次只往后找，如果往前就重复了，比如123和213，因此对于2只往后看
# k影响：第一个位置有k种可能，下一个位置有k-1种可能
self.select(li[j+1:], k - 1, res)
res.pop()
return self.result题解：回溯
要解决 n为100，k为50的情况，暴力写法需要嵌套50层for循环，那么回溯法就用递归来解决嵌套层数的问题。
递归来做层叠嵌套（可以理解是开k层for循环），每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了。
此时递归的层数大家应该知道了，例如：n为100，k为50的情况下，就是递归50层。
可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。
第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。
图中可以发现n相当于树的宽度，k相当于树的深度。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = [] # 存放结果集
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, startIndex, path, result):
if len(path) == k:
result.append(path[:])
return
for i in range(startIndex, n + 1): # 需要优化的地方
path.append(i) # 处理节点
# 这里的i+1 也就是startIndex，限制了只能往后找
self.backtracking(n, k, i + 1, path, result)
path.pop() # 回溯，撤销处理的节点
☆☆☆题解2：剪枝优化
举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = [] # 存放结果集
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, startIndex, path, result):
if len(path) == k:
result.append(path[:])
return
for i in range(startIndex, n - (k - len(path)) + 2): # 优化的地方
path.append(i) # 处理节点
self.backtracking(n, k, i + 1, path, result)
path.pop() # 回溯，撤销处理的节点
216 组合总和II
我的解法：没剪枝
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
result = []
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, starIndex, path, result):
if len(path) == k and sum(path) == n:
result.append(path[:])
return
for i in range(starIndex, 10):# 如果不限制和的时候用9 - (k - len(path)) + 2会报错迭代超出
path.append(i)
self.backtracking(n, k, i+1, path, result)
path.pop()☆☆☆题解：剪枝
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
result = []
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, starIndex, path, result):
if len(path) == k and sum(path) == n:
result.append(path[:])
return
if sum(path) > n:#这里！！！！！！
return
for i in range(starIndex, 9 - (k - len(path)) + 2):
path.append(i)
self.backtracking(n, k, i+1, path, result)
path.pop()17 电话号码的字母组合
☆☆☆我的解法：
注意不用for遍历starIndex
注意这里for循环，可不像是在77和216中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而77和216都是求同一个集合中的组合！
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
letter = [["a","b","c"],["d","e","f"],["g","h","i"],["j","k","l"],["m","n","o"],["p","q","r","s"],["t","u","v"],["w","x","y","z"]]
result = []
if len(digits) == 0:
return []
self.backtracking(letter, digits, 0, "", result)
return result
def backtracking(self, letter, digits, starIndex, path, result):
if len(path) == len(digits):
result.append(path)
return
# for index, i in enumerate(digits[starIndex:]):
i = digits[starIndex]
# if (len(digits[index:]) + len(path)) >= len(digits):
for j in letter[int(i)-2]:
path += j
self.backtracking(letter, digits, starIndex+1, path, result)
path = path[:-1]题解：
注意这里for循环，可不像是在77和216中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而77和216都是求同一个集合中的组合！
注意：输入1 * #按键等等异常情况
代码中最好考虑这些异常情况，但题目的测试数据中应该没有异常情况的数据，所以我就没有加了。
但是要知道会有这些异常，如果是现场面试中，一定要考虑到！
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
self.result = []
self.s = ""
def backtracking(self, digits, index):
if index == len(digits):
self.result.append(self.s)
return
digit = int(digits[index]) # 将索引处的数字转换为整数
letters = self.letterMap[digit] # 获取对应的字符集
for i in range(len(letters)):
self.s += letters[i] # 处理字符
self.backtracking(digits, index + 1) # 递归调用，注意索引加1，处理下一个数字
self.s = self.s[:-1] # 回溯，删除最后添加的字符
def letterCombinations(self, digits):
if len(digits) == 0:
return self.result
self.backtracking(digits, 0)
return self.result题解2：回溯精简
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
self.result = []
def getCombinations(self, digits, index, s):
if index == len(digits):
self.result.append(s)
return
digit = int(digits[index])
letters = self.letterMap[digit]
for letter in letters:
self.getCombinations(digits, index + 1, s + letter)
def letterCombinations(self, digits):
if len(digits) == 0:
return self.result
self.getCombinations(digits, 0, "")
return self.result题解3：回溯精简
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
def getCombinations(self, digits, index, s, result):
if index == len(digits):
result.append(s)
return
digit = int(digits[index])
letters = self.letterMap[digit]
for letter in letters:
self.getCombinations(digits, index + 1, s + letter, result)
def letterCombinations(self, digits):
result = []
if len(digits) == 0:
return result
self.getCombinations(digits, 0, "", result)
return result题解3：使用列表而非字符串
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
def getCombinations(self, digits, index, path, result):
if index == len(digits):
result.append(''.join(path))
return
digit = int(digits[index])
letters = self.letterMap[digit]
for letter in letters:
path.append(letter)
self.getCombinations(digits, index + 1, path, result)
path.pop()
def letterCombinations(self, digits):
result = []
if len(digits) == 0:
return result
self.getCombinations(digits, 0, [], result)
return result
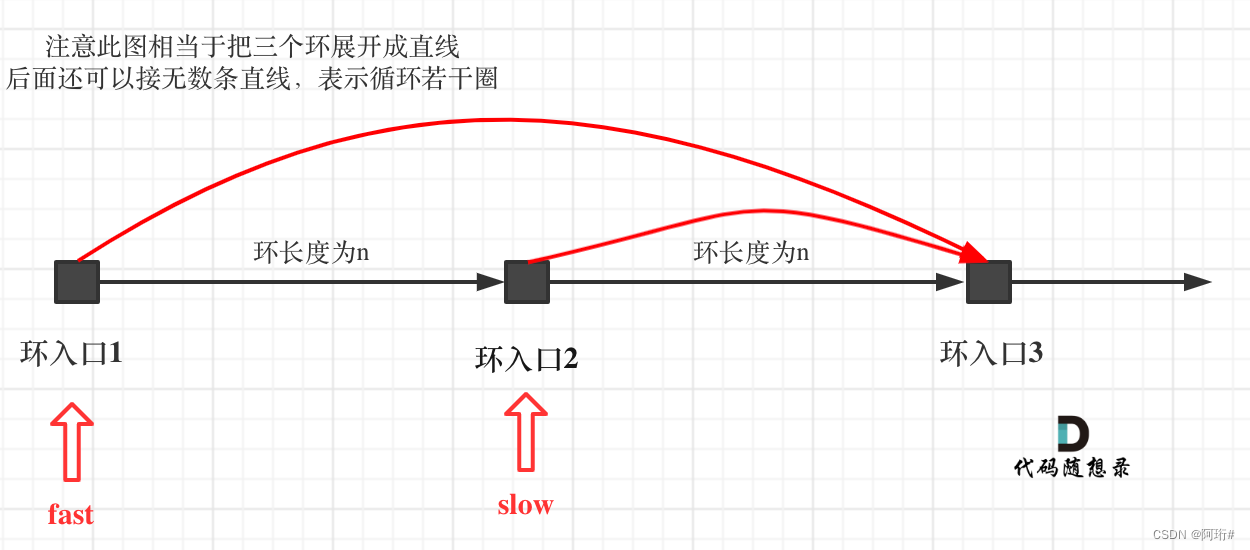
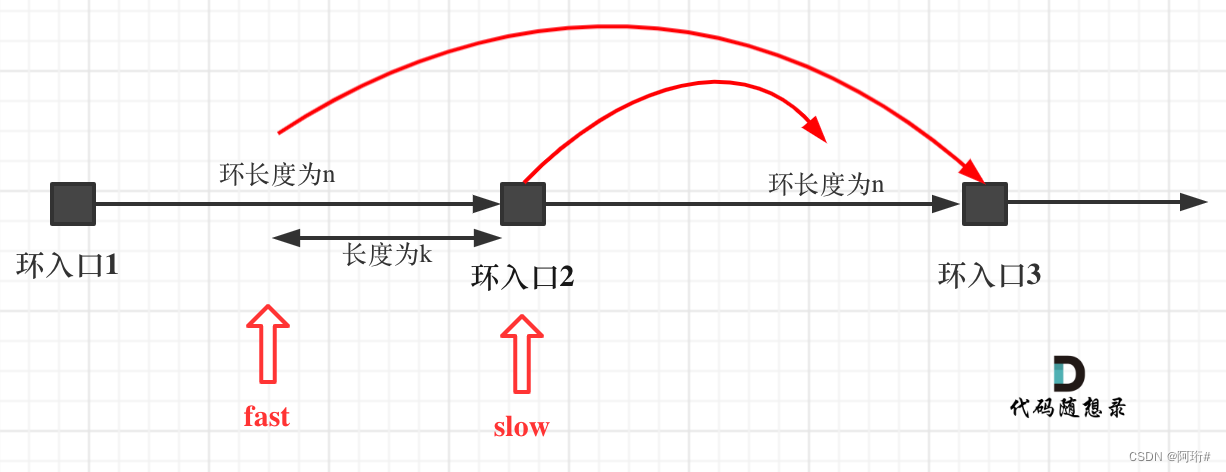
172
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
