【算法】0/1背包问题（蛮力+回溯+分支限界+贪心+非递归-动态规划）C++实现

最新推荐文章于 2024-01-13 14:22:32 发布
最新推荐文章于 2024-01-13 14:22:32 发布
阅读量4.2k 收藏 65
点赞数 10
分类专栏： 算法考研
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45591044/article/details/110876073
版权

分别用蛮力法、回溯法、分支限界法、贪心算法和动态规划法，求解0/1背包问题。

目录

0-1背包问题：

有n件物品和一个容量为W的背包。第i件物品的价值是v[i]，重量是w[i]。求解将哪些物品装入背包可使价值总和最大。所谓01背包，表示每一个物品只有一个，要么装入，要么不装入。

一、简单算法

最简单的算法是：蛮力法，即尝试各种可能的商品组合，并找出价值最高的组合。在这里插入图片描述
这样显然是可行的，但是速度非常慢。在只有3件商品的情况下，你需要计算8个不同的集合；当有4件商品的时候，你需要计算16个不同的集合。每增加一件商品，需要计算的集合数都将翻倍！这种算法的运行时间是O(2ⁿ)，真的是慢如蜗牛。

1）实现代码

#include<stdio.h>
#include<vector>
using namespace std;
vector<vector<int>>ps; //存放幂集
//求1~n的幂集ps
void PSet(int n)
{
    vector<vector<int>>ps1;           //子幂集
    vector<vector<int>>::iterator it; //幂集迭代器
    vector<int>s;
    ps.push_back(s);              //向ps中添加{}空集合
    for (int i = 1; i <= n; i++) {        //循环添加1~n
        ps1 = ps;           //将上一步得到的幂集存放在ps1中
        for (it = ps1.begin(); it != ps1.end(); ++it) {
            (*it).push_back(i);               //每次循环在ps1的每个集合末尾添加i
        }
        for (it = ps1.begin(); it != ps1.end(); ++it) {
            ps.push_back(*it);
        }
    }
}

//求所有方案和最佳方案
void Search(int w[], int v[], int W)
{
    int count = 0;      //方案编号
    int sumw, sumv;    //当前方案的总重量和总价值
    int best_i, best_sumw = 0, best_sumv = 0;        //最佳方案编号、总重量和总价值
    vector<vector<int>>::iterator it;          //幂集迭代器
    vector<int>::iterator sit;    //幂集集合元素迭代器（子迭代器）
    printf("序号\t选择物品\t总重量\t总价值\t能否装入\n");
    for (it = ps.begin(); it != ps.end(); ++it) {
        printf("%d\t", count+1);
        sumw = sumv = 0;
        printf("{");
        for (sit = (*it).begin(); sit != (*it).end(); ++sit) {
            printf("%d", *sit);
            sumw += w[*sit - 1];                           //w数组下标从0开始
            sumv += v[*sit - 1];                           //v数组下标从0开始
        }
        printf("}\t\t%d\t%d\t", sumw, sumv);
        if (sumw <= W) {
            printf("能\n");
            if (sumv > best_sumv) {                        //比较求最优方案
                best_i = count;
                best_sumw = sumw;
                best_sumv = sumv;
            }
        }
        else printf("否\n");
        count++;               //方案编号+1
    }
    printf("0/1背包问题，最佳方案为:");
    printf("选择物品{ ");
        for (sit = ps[best_i].begin(); sit != ps[best_i].end(); ++sit) {
            printf("%d ", *sit);
        }
    printf("},");
    printf("总重量：%d,总价值：%d\n", best_sumw, best_sumv);
}
int main() {
    int n = 4, W = 6;
    int w[] = { 5,3,2,1 };
    int v[] = { 4,4,3,1 };
    PSet(n);    //求1~n的幂集ps
    Search(w, v, W);    //求所有方案和最佳方案
    return 0;
}

2）运行结果图

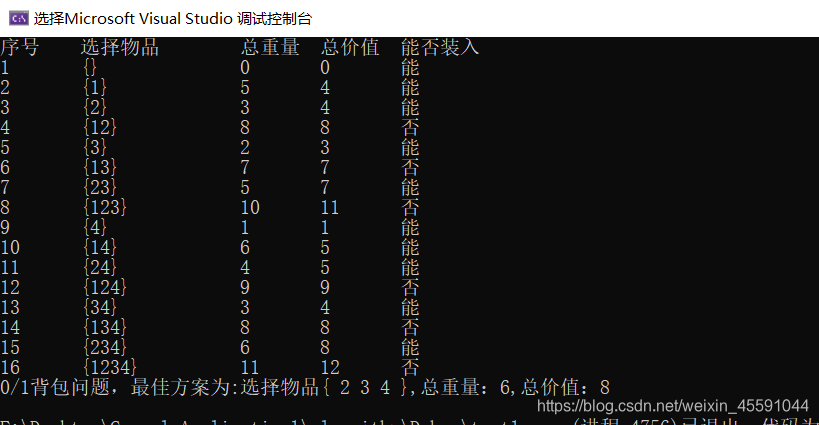
在这里插入图片描述

3）复杂度分析

蛮力法求解0/1背包问题的时间复杂度为：O(2^n)

二、回溯算法

1）实现代码

#include<stdio.h>
#include<iostream>
using namespace std;
#define MAXN 30	//最多物品数
//问题表示
int n, W;	//n个数，W容量
double w[MAXN], v[MAXN];	//物品重量和价值
int x[MAXN];	//存放最终解
int bestp;		//存放最优解的总价值

//求解0/1背包问题
void Backtrack(int t, int tw, int tv, int op[]) 
{
	if (t > n) {		//找到一个叶子结点
		if (tw <= W && tv > bestp) {		//找到一个满足条件的更优解，保存它
			bestp = tv;
			for (int j = 1; j <= n; j++)
				x[j] = op[j];
		}
	}
	else {			//还没搜寻玩所有物品
		if (tw + w[t] <= W) {		//左孩子结点剪枝：满足条件才放入第i个物品
			op[t] = 1;		//选取第i个物品
			Backtrack(t+1,tw+w[t],tv+v[t],op);
		}
		op[t] = 0;		//不选取第i个物品，回溯
		Backtrack(t + 1, tw, tv, op);
	}
}
void disp_bestx() {
	int i;
	int sumw = 0;
	cout << "放入购物车的物品序号为：";
	for (i = 1; i <= n; i++) {
		if (x[i] == 1) {
			cout << i << " ";
			sumw += w[i];
		}
	}
	cout << endl;
	cout << "放入购物车的物品最大价值为：" << bestp << "，总重量为：" << W << endl;
}
int main() {
	cout << "输入物品个数n:"; cin >> n;
	cout << "输入购物车容量W:"; cin >> W;
	cout << "依次输入每个物品的重量w和价值v，用空格分开：";
	for (int i = 1; i <= n; i++) {
		cin >> w[i] >> v[i];
	}
	int op[MAXN];		//存放临时解
	Backtrack(1, 0, 0, op);
	disp_bestx();
	return 0;
}

2）运行结果图

在这里插入图片描述

3）复杂度分析

最不理想的情况下，回溯法求解0/1背包问题的时间复杂度为：O(2^n)
由于其对蛮力法进行优化后的算法，其复杂度一般比蛮力法要小。
空间复杂度：有n个物品，即最多递归n层，存储物品信息就是一个一维数组，即回溯法求解0/1背包问题的空间复杂度为：n。

三、分支限界算法

1）实现代码

#include <iostream>
#define N 30
using namespace std;
int n;double W; //n个数，W容量
double w[N];double v[N];  //物品重量和价值
bool x[N];  
bool best_x[N]; //存储最优方案
double now_v;   //当前价值
double remain_v;    //剩余价值
double now_w;   //当前容量
double best_v;  //最优价值
double Bound(int k)     //计算分枝结点k的上界
{
    remain_v = 0;
    while (k <= n) {
        remain_v += v[k];
        k++;
    }
    return remain_v + now_v;
}
void Backtrack(int t)
{
    if (t > n) {  //是否到达叶节点
        for (int i = 1; i <= n; i++) {
            best_x[i] = x[i];   //记录回溯的最优情况
        }
        best_v = now_v; //记录回溯中的最优价值
        return;
    }
    if (now_w + w[t] <= W) {  //约束条件，是否放入。放入考虑左子树，否则考虑右子树
        x[t] = 1;
        now_w += w[t];
        now_v += v[t];
        Backtrack(t + 1); //进行下一个节点的分析
        now_w -= w[t];  //在到达叶节点后进行回溯
        now_v -= v[t];
    }
    if (Bound(t + 1) > best_v) {    //限界条件，是否剪枝。若放入t后不满足约束条件则进行到此处，然后判断若当前价值加剩余价值都达不到最优，则没必要进行下去
        x[t] = 0;
        Backtrack(t + 1);
    }
}
void Knapsack(double W, int n)
{
    double sum_w = 0;
    double sum_v = 0;
    best_v = 0;
    for (int i = 0; i < n; i++) {
        sum_w += w[i];
        sum_v += v[i];
    }
    Backtrack(1);
    cout << "放入购物车的物品最大价值为：" << best_v << endl;
    cout << "放入购物车的物品序号为：" << endl;
    for (int i = 1; i <= n; i++) {
        if(x[i] == 1)
            cout << i << " ";
    }
}
int main()
{
    cout << "输入物品个数n:"; cin >> n;
    cout << "输入购物车容量W:"; cin >> W;
    cout << "依次输入每个物品的重量w和价值v，用空格分开：\n";
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> v[i];
    }
    Knapsack(W, n);
    return 0;
}

2）运行结果图

在这里插入图片描述

3）复杂度分析

分支限界法求解0/1背包问题的时间复杂度为：O(2^n)

四、贪心算法

1）实现代码

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define MAXN 51
int n;
int W;
struct NodeType
{
	int w;
	int v;
	int p;				//性价比p=v/w
	bool operator<(const NodeType& s)const
	{
		return p > s.p;
	}
};
NodeType A[MAXN];
int maxv;
int x[MAXN];
void Knap()						//求解背包问题并返回总价值
{
	maxv = 0;					//maxv初始化为0
	int weight = W;				//背包中能装入的余下重量	
	memset(x, 0, sizeof(x));	//初始化x向量
	int i = 1;
	while (A[i].w <= weight)		//物品i能够全部装入背包时，循环
	{
		x[i] = 1;				//装入物品i
		weight -= A[i].w;		//减少背包中能装入的余下重量
		maxv += A[i].v;			//计算装入物品i后的总价值
		i++;
	}
}
void disp_bestx() {
	int sumw = 0;
	cout << "放入购物车的物品序号为：";
	for (int j = 1; j <= n; j++) {
		if (x[j] == 1) {
			cout << j << " ";
			sumw += A[j].w;
		}
	}
	cout << endl;
	cout << "放入购物车的物品最大价值为：" << maxv << "，总重量为：" << sumw << endl;
}
int main()
{
	cout << "输入物品个数n:"; cin >> n;
	cout << "输入购物车容量W:"; cin >> W;
	cout << "依次输入每个物品的重量w和价值v，用空格分开：" << endl;;
	for (int i = 1; i <= n; i++) {
		cin >> A[i].w >> A[i].v;
	}
	for (int i = 1; i <= n; i++) {
		A[i].p = A[i].v / A[i].w;
	}
	sort(A + 1, A + 1 + n);
	Knap();
	disp_bestx();
	return 0;
}

2）运行结果图

在这里插入图片描述

3）复杂度分析

贪心法求解0/1背包问题的时间复杂度为：O( nlog(n) )

五、非递归-动态规划

1）实现代码

#include<stdio.h>
#include<iostream>
using namespace std;
#define max(x,y) ((x)>(y)?(x):(y))
#define MAXN 30		//最多物品数
#define MAXW 100	//最大限制重量
//问题表示
int n, W;	//n个数，W容量
int w[MAXN], v[MAXN];	//物品重量和价值
//求解结果表示
int dp[MAXN][MAXW];
int x[MAXN];
int bestp;		//存放最优解的总价值
//用动态规划法求0/1背包问题
void Knap()
{
	int i, r;
	for (i = 0; i <= n; i++)	//置边界条件dp[i][0] = 0
		dp[i][0] = 0;
	for (r = 0; r <= W; r++)	//置边界条件dp[0][r] = 0
		dp[0][r] = 0;
	for (i = 1; i <= n; i++) {
		for (r = 1; r <= W; r++) {
			if (r < w[i])
				dp[i][r] = dp[i - 1][r];
			else
				dp[i][r] = max(dp[i - 1][r], dp[i - 1][r - w[i]] + v[i]);
		}
	}
}
void Buildx()		//回推求最优解
{
	int i = n, r = W;
	bestp = 0;
	while (i >= 0) {
		if (dp[i][r] != dp[i - 1][r]) {
			x[i] = 1;
			bestp += v[i];
			r = r - w[i];
		}
		else
			x[i] = 0;
		i--;
	}
}
int main() {
	cout << "输入物品个数n:"; cin >> n;
	cout << "输入最大容量W:"; cin >> W;
	cout << "依次输入每个物品的重量w和价值v，用空格分开：";
	for (int i = 1; i <= n; i++) {
		cin >> w[i] >> v[i];
	}
	Knap();
	Buildx();
	printf("最优方案\n");
	printf("选取物品为：");
	for (int i = 1; i <= n; i++)
		if (x[i] == 1)
			printf("%d ", i);
	printf("\n");
	printf("总价值=%d\n", bestp);
	return 0;
}

2）运行结果图

在这里插入图片描述

3）复杂度分析

动态规划法求解0/1背包问题的时间复杂度为：O(nW)
空间复杂度为：O(nW)

infinite_with
关注
  • 10
    点赞
  • 踩
  • 65
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
0-1背包动态规划回溯法分支限界贪心算法
12-05
本资源包含了0-1背包问题的最佳所有解法，其中包括动态规划算法，回溯法算法，分支限界算法和贪心算法。包含源代码。
动态规划法、贪心算法、回溯法、分支限界法解决0-1背包
11-23
1) 动态规划法求解问题的一般思路，动态规划法求解本问题的思路及其C/C++程序实现与算法的效率分析。 2) 贪心算法在0-1背包问题求解中的应用 3) 回溯法求解问题的一般思路，回溯法求解本问题的思路及其C/C++程序实现与算法的效率分析。 4) 分支限界法求解问题的一般思路，分支限界法求解本问题的思路及其C/C++程序实现与算法的效率分析。 有代码！！
0/1背包问题（蛮力、动态规划、回溯、分支限界法）
01-20
算法设计实验报告，包括：蛮力、动态规划、回溯、分支限界四种算法求解0/1背包问题的基本思想、时间复杂度分析，C++实现代码，运行结果截图，实验心得。
基于C++的分支限界算法来解决问题的一些程序，包括分支限界法解决0/1背包和TSP问题+源代码+文档说明
01-12
基于C++的分支限界算法来解决问题的一些程序，包括分支限界法解决0/1背包和TSP问题+源代码+文档说明 - 不懂运行，下载完可以私聊问，可远程教学 该资源内项目源码是个人的毕设，代码都测试ok，都是运行成功后才上传资源，答辩评审平均分达到96分，放心下载使用！ <项目介绍> 1、该资源内项目代码都经过测试运行成功，功能ok的情况下才上传的，请放心下载使用！ 2、本项目适合计算机相关专业(如计科、人工智能、通信工程、自动化、电子信息等)的在校学生、老师或者企业员工下载学习，也适合小白学习进阶，当然也可作为毕设项目、课程设计、作业、项目初期立项演示等。 3、如果基础还行，也可在此代码基础上进行修改，以实现其他功能，也可用于毕设、课设、作业等。 下载后请首先打开README.md文件（如有），仅供学习参考, 切勿用于商业用途。 --------
0-1背包问题 动态规划 分支限界 回溯 贪心四种方法
05-26
0-1背包问题 动态规划 分支限界 回溯 贪心四种方法
C语言【微项目09】—背包问题0/1[用二进制逐次加一生成集合子集]（采用蛮力法实现）【2021-11-24】
TDTX博客
11-24 839
C语言【微项目09】—背包问题0/1[用二进制逐次加一生成集合子集]（采用蛮力法实现）【2021-11-24】FMethodPackage.c运行结果示例1.5个物品，负重152.20个物品，负重200 【TDTX】 FMethodPackage.c #include <stdio.h> #include <math.h> #include <stdlib.h> int main() { int n,fz; int i,j; printf("输入物
[算法课]五种蛮力法解决01背包问题
代码中枢：软件工程理论与实践的桥梁
04-30 7288
注明：蛮力法 算法标签：全排列，枚举 题目简介 0/1背包问题【算法中非常经典的一个例题，多种不同的算法可以来实现】 有n个重量分别是w1,w2…,wn的物品（物品编号为1-n） 它们的价值分别为v1,v2,…,vn 给定一个容量为W的背包。设计从这些物品中选取一部分放入该背包的方案。 每个物品要么选中要么不选中【每种物品是唯一的】， 要求选中的物品不仅能够放在背包中【能放得下】，而且具有最大的价...
算法分析与设计——蛮力法0/1背包
Flamingo的博客
11-22 8093
蛮力法0/1背包 蛮力法 蛮力法是一种简单直接解决问题的方法，常常直接基于问题的描述，所以蛮力法也是最容易应用的方法。 蛮力法所依赖 的基本技术是遍历，即采用一定的策略依次处理待求解问题的所有元素，从而找出问题的解。由于其需要依次穷举待处理的元素，因此蛮力法是一种典型的指数级时间算法。 问题 给定n个重量为{w1,w2,···,wn}、价值为{v1,v2,···,vn}的物品和一个容量为C的背包，0/1背包是一个求解这些物品中的一个最有价值的子集，并且能够装入到背包中。 应用实例 有n项可投资的项目，每个项
蛮力法求解0/1背包问题
LixDemon的博客
03-15 2419
问题描述 有n个重量分别为{w1，w2，…，wn}的物品，它们的价值分别为{v1，v2，…，vn}，给定一个容量为W的背包。设计从这些物品中选取一部分物品放入该背包的方案，每个物品要么选中要么不选中，要求选中的物品不仅能够放到背包中，而且具有最大的价值。 并对下表所示的4个物品求出W=6时的所有解和最佳解。 问题求解 对于n个物品、容量为W的背包问题，采用前面求幂集的方法求出所有的物品组合。 对...
0-1 背包问题的 4 种解决方法&&算法策略
热门推荐
Tyler_Zx的博客
11-01 6万+
蛮力法 递归与分治策略 动态规划 贪心算法 回溯法 分支限界法 前言 0-1背包是一个经典的问题，而它能用不同的算法思想去解决。恰巧最近在看算法，学习算法就是学习解决问题的思路。现在将0-1背包问题与解决方法整理出来，这样不仅能区分不同的算法思想，还能加深对0-1背包问题的理解。虽然有的算法思想并不能解决这一问题，但是为了对算法策略有一个较为整体的了解，所以在这里做一下简单的介绍。 ...
蛮力法解决0_1背包问题新思路-——利用C语言位域类型
weixin_30675247的博客
04-10 665
废话不说了，直接上代码 #include<stdio.h> #include<math.h> #define N 5 //物品种类数目 #define CAPACITY 6 //背包容量 #define COUNT 32 int weight[N]={3,2,1,4,5}; int value[N]={25,20,15,40,50}; union{...
求解0/1背包问题 蛮力法即暴力算法实现
＃两个西柚
04-20 3658
求解0/1背包问题 【问题描述】 有n个重量分别为{w1,w2,…,wn}的物品，它们的价值分别为{v1,v2,…,vn},给定一个容量为w的背包，实际从这些物品中选取一部分物品放入该背包的方案，每个物品要么选中要么不选中，要求选中的物品不仅能够放到背包中，而且要具有最大的价值。 【问题求解】对于n个物品、容量为w的背包问题，采用前面求幂集的方法求出所有物品组合。 对于每一种组合，计算其总重量su...
（C语言动态规划算法）0/1背包问题
qq_61832536的博客
01-02 7024
Description 已知一个载重为M的背包和n件物品，物品编号从0到n-1。第i件物品的重量为wi，若将第i种物品装入背包将获益pi，这里，wi>0，pi>0，0<=i<n。所谓0/1背包问题是指在物品不能分割，只能整件装入背包或不装入的情况下，求一种最佳装载方案使得总收益最大。 Input 第1行中有2个正整数n（n<=50）和M，表示有n件物品，背包载重为M(m<=100)。然后输入n个物品的重量，最后输入n个物品的收益值。 ...
算法学习笔记9——蛮力法和动态规划法求解0/1背包问题
weixin_44342332的博客
05-18 1027
完整代码： #include<iostream> #include <windows.h> #include<iomanip> using namespace std; int c; //背包的容量 int bag_values=0;//背包（装入）的价值 初始化为0 int goods_num; //货物的数量 int maxValue = -1; //定义最大的价值 int calc_arrangement(); //函数 在后面实现 /*结构体 物
蛮力法解决01背包问题，详细讲解，c语言，c++
最新发布
m0_62330079的博客
01-13 770
蛮力法求解01背包问题，详细讲解
01背包的两种基础解法（动态规划、直接递归）（C语言）
feng_hang_的博客
09-06 376
(容量为C，面对N个物体的最大价值)==MAX（容量为C-1，面对N-1个物体的最大价值），（容量为C-w[n]，面对N-1个物体的最大价值）+v[n]动态规划的二维表可以避免递归的大量重复运算，从而提高效率。我们本能地会想到递归，也就是方法一。，当问题的递推公式找到后，
算法设计与分析—蛮力法
wxh的博客
02-27 2176
蛮力法解决 查住问题，排序问题，串匹配问题，哈密顿问题，01背包问题
蛮力法解决01背包问题（递归）
m0_71385141的博客
10-27 484
问题描述：给定n个重量为{w1, w2, …,vn}的物品和一个容量为C的背包，求这些物品中的一个最有价值的子集，且要能够装到背包中。(2)熟练设计和生成问题的解空间：设计一种穷举策略将物品装入背包的各种装法都找出来，并能够在计算机中存储和表示。：对递归算法不熟悉的学生，可以先做一个练习：设计一个递归函数，实现计算N的阶乘。物品2：重量12kg，价值4$物品5：重量4kg，价值10$物品1：重量2kg，价值2$物品3：重量1kg，价值2$物品4：重量1kg，价值1$(3)理解蛮力法的局限性；
0/1背包回溯法+分支限界法 c++
06-06
以下是0/1背包问题的回溯法和分支限界法的C++代码： 回溯法： ```c++ #include <iostream> #include <vector> using namespace std; int n, W; vector<int> w, v; int maxv = 0; void dfs(int i, int cw, int cv) { if (i == n) { if (cv > maxv) maxv = cv; return; } dfs(i + 1, cw, cv); if (cw + w[i] <= W) { dfs(i + 1, cw + w[i], cv + v[i]); } } int main() { cin >> n >> W; w.resize(n); v.resize(n); for (int i = 0; i < n; i++) { cin >> w[i] >> v[i]; } dfs(0, 0, 0); cout << maxv << endl; return 0; } ``` 分支限界法： ```c++ #include <iostream> #include <vector> #include <queue> using namespace std; int n, W; vector<int> w, v; int maxv = 0; struct Node { int cw, cv, i; bool operator<(const Node& other) const { return cv < other.cv; } }; void bfs() { priority_queue<Node> q; q.push({0, 0, 0}); while (!q.empty()) { Node u = q.top(); q.pop(); if (u.i == n) { if (u.cv > maxv) maxv = u.cv; continue; } if (u.cw + w[u.i] <= W) { q.push({u.cw + w[u.i], u.cv + v[u.i], u.i + 1}); } q.push({u.cw, u.cv, u.i + 1}); } } int main() { cin >> n >> W; w.resize(n); v.resize(n); for (int i = 0; i < n; i++) { cin >> w[i] >> v[i]; } bfs(); cout << maxv << endl; return 0; } ``` 这里的回溯法和分支限界法都是使用了搜索的思想，回溯法是通过递归的方式枚举所有可能的情况，而分支限界法则是通过优先队列的方式，每次取出当前最优的节点进行拓展。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值