系列文章目录
CutAddPaste:利用异常知识进行时间序列异常检测
文章目录
摘要
由于异常的稀有性和样本类别的不平衡,检测时间序列异常极其复杂,这通常会导致异常标记成本高昂且具有挑战性。 大多数现有方法很大程度上依赖于正态性假设,忽略了标记的异常样本。 虽然基于异常假设的方法可以结合异常的先验知识来在训练分类器中进行数据增强,但所采用的随机或粗粒度增强方法仅关注逐点异常并且缺乏前沿领域知识,使得它们不太可能获得更好的性能。 本文介绍了 CutAddPaste,这是一种基于异常假设的新颖方法,用于检测时间序列异常。 它主要采用数据增强策略,通过尽可能多地利用异常的先验知识来生成伪异常。 CutAddPaste的核心是从时间子序列样本中的随机位置剪切块,添加线性趋势项,并将其粘贴到其他样本中,从而可以很好地逼近各种异常,包括点异常和模式异常。 标准基准数据集上的实验表明,我们的方法优于最先进的方法。
一、引言
时间序列数据中异常检测(AD)的主要任务是检测与大多数时间段显着不同的异常时间段。 有效的AD检测是工业设备、网络入侵检测、监测患者生命体征等应用的基石。与二元分类不同,AD旨在识别很少发生的事件——在这种情况下,异常实例与正常实例相比相当稀疏 。 此外,准确标记的样本还远远不够,因为标记时间序列异常通常需要大量的专业知识和精力,这在数据密集型深度模型等大规模异常检测任务中是昂贵且不切实际的。
因此,将 AD 视为一种无监督学习过程已成为一种常见做法。 大多数现有工作——包括自动编码器[1]、一类分类[2]和一类对比[3]——都是建立在单/多重正态性假设的基础上的。 关键的见解是训练集中没有或只有少数异常样本。 如图1(a)所示,这些方法将所有未标记的训练数据视为正常数据,并依赖于各种借口任务来学习正常样本的表示。 显然,训练集中一些异常实例(例如,领域专家注释的一小部分异常)背后的固有语义信息没有得到充分利用,并且会导致检测效果较差。

图 1:AD 方法中使用的正态性和异常假设的示意图。 存在异常子组 𝐴1、𝐴2 和 𝐴3。 红色虚线是预定义的阈值。 a) 擅长识别分布之外的异常,例如 𝐴1。 b) 可以借助增强来识别正常样本中混合的异常,如 𝐴2,但在没有增强的情况下无法做到这一点,如 𝐴3。
为了利用此类标记的异常,进行了大量的后续研究,包括异常值暴露 (OE) [4]、CutPaste [5] 和 Deep SAD [6]。 它们基于异常假设,并在实践中生成异常样本,在先验异常知识的指导下,训练深度分类器(见图1(b))。 然而,它们都致力于解决图像领域的问题,并不能直接应用于时间序列异常检测(TSAD)模型,因为时间序列中异常的时间依赖性和类型完全不同。 NCAD [7] 是极少数支持时间序列 AD 的尝试之一。 受 OE 的启发,它结合了上下文随机点异常值来生成模拟异常。 然而,现有的基于异常假设的技术仅通过采用简单化和初级的方式生成随机异常或点异常,忽略了异常的复杂先验知识。 这种简单的增强是不现实的,并且很难提高异常检测的准确性和有效性。 事实上,时间序列异常以更加异构的方式表现出来——除了随机异常和点异常之外,还有许多其他类型的异常,特别是点异常(全局或上下文)和模式异常(shapelet、季节性、 或趋势)异常[8],现有方法尚未解决这些问题。 作为 shapelet [9] 的一个特例,多变量时间序列的相关性也被忽略。
本文提出了 CutAddPaste,一种基于异常假设的新颖解决方案,由一系列具有更丰富的异常先验知识的数据增强技术支持。 主要目标是创建不规则的子序列,可以作为真正的逐点和模式异常的近似值。 为了实现这一点,我们从时间序列子序列样本中的随机位置剪切一个补丁,添加线性趋势分量,最后将其粘贴到另一个样本中的任意位置。 随后,原始时间序列和增强对应物被输入到时间卷积网络(TCN)层和投影层,以计算具有相应标签的交叉熵损失。 我们对 AIOps、UCR、SWaT 和 WADI 等四个数据集进行了广泛的实验,并采用修订点调整 (RPA) 指标 [10] 作为性能指标。 实验结果表明,我们的方法在 TSAD 任务中优于其他基线。 附录中详细介绍了使用其他指标(例如调整点 (PA) 指标 [11])的广泛结果,以证明 RPA 的公平性。
具体来说,这项工作做出了以下贡献:
• 据我们所知,CutAddPaste 是第一个可以解决 TSAD 深度模型的复杂异常增强问题的工作,而不是简单地使用朴素的点注入。
• CutAddPaste 是一种专为 TSAD 量身定制的优雅简单但功能强大的数据增强技术。 利用异常知识,CutAddPaste 拓宽了点异常的范围,涵盖了模式异常,例如 shapelet、季节性和趋势。
• 对涵盖单变量和多变量数据的 4 个真实世界数据集进行的实验证明了我们方法的卓越性能。 六个指标之间的比较也表明了使用 RPA 指标的建议。
2 RELATEDWORK
无监督深度学习方法通常为从大量数据集中进行异常检测奠定了基础。 其中,最流行的方法涉及提取正常样本的表示,通常称为“正态性假设”[12]。相应地,某些方法侧重于辨别异常的显着特征。我们将这些技术归类为“方法”。 基于异常假设。” 下面是对这两个类别的简要概述。
基于正态性假设的方法。 有些方法的前提是大多数收集的训练数据都是正常的。 他们构建了所谓常态的复杂表示,将与这些表示不相符的数据指定为异常。 基于GAN的[13, 14]、基于自动编码器的[1]、基于一类的[2]和基于聚类的[15]方法是代表。 最值得注意的是,基于自动编码器的方法假设正常样本比异常样本可以更好地从潜在空间重建。 虽然它们提供了对常态的不同见解,但在全面了解常态时可能会带来某些限制和偏见。 研究人员努力整合这些假设,以更好地涵盖正常特征。 一些方法,例如[16],采用两阶段机制——提取整个数据集的表示并利用内在正态性来识别异常。 为了消除与AD无关的特征的潜在负面影响,[3]和[17]将一些先前的假设结合到一个统一的过程中,构建了一个包罗万象的常态描述。 然而,确定这种融合是否完全体现了正态性仍然具有挑战性,并且假设的不断合并甚至会加剧模型的收敛问题。 此外,未充分利用有价值的先验知识将阻碍模型训练的有效性,使学习过程从头开始。
基于异常假设的方法。 虽然正常状态可能难以捉摸,但研究人员对异常状态有一定的了解。 他们利用随机伪异常来训练分类器。 离群值暴露(OE)[4]在训练期间集成来自外部数据集的数据,将模型暴露于分布外的实例,以学习正常样本的更保守的概念,从而可以提高对未知异常模式的检测。 深度半监督异常检测(Deep SAD)[6]是深度SVDD[2]的扩展,它在模型中纳入了已知的异常,并且可以在潜在分布中表现出比正常样本更高的交叉熵。 在计算机视觉 (CV) 背景下,CutPaste [5] 采用数据增强技术(例如,涉及图像块的切除并放置在较大图像的随机位置并产生空间不规则性)来提供图像缺陷的基本模拟 。 [18]表明,要产生最先进的检测性能,需要相对较少的随机 OE 样本。 NCAD [7] 通过将混合的上下文异常和随机点异常注入时间序列数据,使 OE 方法适应时间序列场景,以在正常类和异常类之间建立可辨别的边界。 然而,流行的方法只是以随机或粗略的方式生成伪异常,强调了领域知识的重要性。 这一见解促使我们将“CutPaste”方法改进到时间序列领域。 为此,我们生成了一系列异常现象,包括异常季节、趋势和形状等模式。 表1详细地从不同角度对我们的方法和其他相关工作进行了比较。
3 OUR APPROACH
3.1 Problem Definition
给定一个有序时间序列 S = { x 1 , x 2 , … , x l } \mathcal{S}=\{x_{1},x_{2},\ldots,x_{l}\} S={x1,x2,…,xl}在 𝑙 长度的时间段内收集。 x i ∈ R d x_i\in\mathbb{R}^d xi∈Rd 是在时间戳 𝑖 收集的 𝑑 维向量。 如果 𝑑 = 1,时间序列将表示为单变量,如果 𝑑 > 1,则表示为多变量。传统方法通常将长时间序列 S 分割为一组时间子序列,即 D = { X 1 , X 2 , … , X N } \mathcal{D}=\{\mathbf{X}_{1},\mathbf{X}_{2},\ldots,\mathbf{X}_{N}\} D={X1,X2,…,XN}通过滑动窗口,其长度设置为𝑡。 样本 X i = { x 1 , x 2 , … , x t } \mathbf{X}_{i}=\{x_{1},x_{2},\ldots,x_{t}\} Xi={x1,x2,…,xt}是时间子序列内点的集合,𝑁 是样本数。 时间步 𝛿 ≤ 𝑡 是滑动的步幅,如果 𝛿 < 𝑡 则样本重叠。 为了更好地描述模式异常的特征,我们采用结构建模[8]将时间序列样本表示为 X = Γ ( 2 π ω T ) + Θ ( T ) X = \Gamma(2\pi\omega T)+\Theta(T) X=Γ(2πωT)+Θ(T),其中𝑇 = {1, 2, . 。 。 ,𝑡}。 Γ \Gamma Γ定义了基本的shapelet函数,它不仅描述了时间序列的形状,还包含了各个维度之间的关系。 这些关系可以通过协方差矩阵 𝑐𝑜𝑣 (𝑋, 𝑋) 来描述。 𝜔 是季节性,θ 是描述 X i \mathbf{X}_{i} Xi方向的趋势函数。 相应地,D 有一组标签 Y = { y 1 , y 2 , … , y N } \mathcal{Y} = \{y_{1},y_{2},\ldots,y_{N}\} Y={y1,y2,…,yN}和 y i ∈ { 0 , 1 } y_{i}\in\{0,1\} yi∈{0,1} 表示样本 X i \mathbf{X}_{i} Xi是正常 (0) 或异常 (1)。 目标是在给定时间序列 X i \mathbf{X}_{i} Xi的情况下预测标签 y ^ i ∈ { 0 , 1 } \hat{y}_{i}\in\{0,1\} y^i∈{0,1} 。 我们计算异常分数 S i \mathbf{S}_{i} Si,而不是直接给出二进制标签,并且可以通过将 S i \mathbf{S}_{i} Si 与预定义阈值 𝜏 进行比较来获得预测标签。
表1:相关工作的比较。 N和A代表该方法是否使用正常和异常样本。 G 和 C 是全局和上下文点异常。 SL、SE 和 T 是形状异常、季节性或趋势模式异常。

3.2 Overview
我们方法的核心思想是通过数据增强增强基于窗口的异常检测方法。 图 2 显示了所提出的模型架构,由用于异常注入的 CutAddPaste 增强模块和深度 TSAD 模型组成,该模型具有用于特征提取的编码器和用于矢量映射的投影仪。 CutAddPaste 增强是为 TSAD 的任务而设计的,据我们所知,这是在时间序列中注入所有五种异常类型的首次尝试。 受到图像领域CutPaste [5]的启发,我们以基于窗口的方式扩展并实现它,以更有效地处理时间序列。 除了模式异常(形状和季节性)之外,我们还引入了一个重要的趋势术语来生成趋势、相关性和逐点异常。
特别是,原始时间序列被归一化以实现零均值和单位方差。 我们使用𝑡大小的时间窗口将时间序列分割成几个子序列。 其中一些被输入到基于先验的数据增强模块 CutAddPaste 中,其中强制执行一组操作来生成伪异常,例如图 2 中的 X a \mathrm{X}_{a} Xa。从技术上讲,我们从时间子序列样本中的随机位置剪切补丁,添加线性 趋势术语,并将其粘贴到其他示例中。 因此,伪异常样本 D P \mathcal{D}_{P} DP 的集合以及真实样本 D R \mathcal{D}_{R} DR 和标签 Y 可以用于进一步的模型训练和评估。 CutAddPaste 的细节将在 3.3 节中讨论。
随后,设计了一个 TCN
f
θ
:
D
↦
C
f_\theta:\mathcal{D}\mapsto C
fθ:D↦C 编码器,将 𝑡 大小的
X
i
\mathbf{X_i}
Xi 转换为固定大小的向量表示
z
i
\mathbf{z_i}
zi。 它由三个时间卷积块实现,每个块由 Conv1D 层、Batch Normalization (BN) 层、ReLU 激活函数和 MaxPool1D 层组成。 第一个块包含一个附加的 Dropout 层。 表示
z
i
\mathbf{z_i}
zi被输入可学习的非线性投影仪
g
θ
:
C
↦
Q
g_{\theta}:C\mapsto Q
gθ:C↦Q 来输出投影
z
i
\mathbf{z_i}
zi 。 该投影仪应用具有一个隐藏层的 MLP,该隐藏层使用 BN 和 ReLU 激活函数。 它将从特征编码器获得的表示映射到二维投影空间。 该映射是通过计算交叉熵损失来指导的,这将在第 3.4 节中详细介绍
 图 2:CutAddPaste 概述。 它通过首先从样本
X
j
X_{j}
Xj中剪切一个补丁,在补丁的某些维度上添加趋势项,最后将其粘贴到另一个任意
X
i
X_{i}
Xi上来生成伪异常
X
a
X_{a}
Xa。 所有真实样本,例如
X
k
X_{k}
Xk ,并将伪异常样本输入 TCN 以学习异常的概率分数。
图 2:CutAddPaste 概述。 它通过首先从样本
X
j
X_{j}
Xj中剪切一个补丁,在补丁的某些维度上添加趋势项,最后将其粘贴到另一个任意
X
i
X_{i}
Xi上来生成伪异常
X
a
X_{a}
Xa。 所有真实样本,例如
X
k
X_{k}
Xk ,并将伪异常样本输入 TCN 以学习异常的概率分数。
3.3 Data Augmentation
范围界定。 CutAddPaste 旨在增强最新类型的时间序列,并将其用作下游检测任务中的先验知识。 按照[8]中提出的时间异常的定义,我们深入研究了逐点和模式方面的异常行为。 逐点异常是指显着偏离全局点或上下文点的点,而模式异常包括shapelet异常、季节性异常和趋势异常。 更具体地,小形状异常包括与正常子序列相比表现出明显形状差异的形状异常和指变量之间的异常依赖性的相关异常。 季节性和趋势异常值呈现不寻常的季节性或趋势。
关键技术。 如图2所示,我们在S被滑动窗口切割成许多等长样本后,进行了面向时间数据的基于窗口的增强。 我们生成一个新的异常样本补丁,并将该补丁替换为样本 X i X_{i} Xi的随机位置,即 X i X_{i} Xi的原始值被替换。 特别是,我们设计了以下步骤来生成具有所有五种异常类型的样本。
• 剪切:我们从另一个任意选择的样本 𝑋𝑗 中剪切出随机大小的 𝑟 ≥ 𝜁 子序列的补丁,其中超参数 𝜁 ∈ (0, 𝑡) 控制补丁的最小长度,因为长度必须足够长才能生成异常。
• 添加:我们添加一系列增量或减量值 V t r e n d V_{trend} Vtrend,这些值源自具有随机斜率的线性函数到补丁。 对于多维时间序列,我们选择性地选择并聚合其中一些维度以形成随机趋势并将它们添加到剪切块中。
• 粘贴:我们将补丁嵌入到样本 X i X_{i} Xi的随机位置。 该位置中预先存在的值将被补丁中的值替换。
分析。 给定粘贴(目标)样本 X i = Γ i ( 2 π ω i T ) + \mathbf{X}_{i}=\Gamma_{i}(2\pi\omega_{i}T)+ Xi=Γi(2πωiT)+ Θ i ( T ) \Theta_{i}(T) Θi(T) 和剪切(源)样本 X j = Γ j ( 2 π ω j T ) + Θ j ( T ) \mathbf{X}_{j}=\Gamma_{j}(2\pi\omega_{j}T)+\Theta_{j}(T) Xj=Γj(2πωjT)+Θj(T),其中 𝑇 = {1, 2, . 。 。 ,𝑡}。 X i a n d X j \mathrm{X}_{i}\mathrm{~and~X}_{j} Xi and Xj来自S,已经标准化。 趋势项 V t r e n d = ρ ⋅ m ⋅ R V_{trend} = \rho\cdot m\cdot R Vtrend=ρ⋅m⋅R,其中 𝑅 = {1, 2, . 。 。 ,𝑟}。 m = ( m 1 , m 2 , … , m d ) m = (m_{1},m_{2},\ldots,m_{d}) m=(m1,m2,…,md)是 d 维随机斜率向量,其中 -1 < m i m_i mi < 1。超参数 𝜌 > 0 控制趋势项的程度。 经过上述增广操作后,伪异常样本 X𝑎 定义为: { x b ∣ b ∈ T } \{x_{b}|b\in T\} {xb∣b∈T} ,涉及 X i , X j , a n d V t r e n d \mathbf{X}_i,\mathbf{X}_j,\mathrm{~and~}\mathbf{V}_{trend} Xi,Xj, and Vtrend 的𝑋𝑎公式如下:

其中
k
=
k
j
−
k
i
,
k
′
=
k
i
−
1.
k
i
<
t
−
r
a
n
d
k
j
<
t
−
r
k = k_{j} - k_{i}, k^{'} = k_{i} - 1. k_{i} < t-r \mathrm{and} k_{j} < t-r
k=kj−ki,k′=ki−1.ki<t−randkj<t−r 分别是随机粘贴位置和剪切位置。 如图3所示,考虑子序列
X
[
t
1
:
t
2
]
X[t_{1}:t_{2}]
X[t1:t2],即
{
x
t
1
,
x
t
1
+
1
,
…
,
x
t
2
}
\begin{Bmatrix}x_{t_{1}},x_{t_{1}+1},\ldots,x_{t_{2}}\end{Bmatrix}
{xt1,xt1+1,…,xt2},我们将以下五种相关的异常类型制定到𝑋𝑎上:
• A1-S:形状。 一般来说,
Γ
i
\Gamma_{i}
Γi与
Γ
j
\Gamma_{j}
Γj不同,因为
X
j
X_{j}
Xj 是随机选择的。 因此,从
t
1
∈
[
1
:
k
i
)
t_{1}\in[1:k_{i})
t1∈[1:ki)到
t
2
∈
[
k
i
+
1
,
T
]
t_{2}\in[k_{i}+1,T]
t2∈[ki+1,T] 的任意子序列
X
a
[
t
1
:
t
2
]
X_a[t_1:t_2]
Xa[t1:t2] 包含形状函数 Γ 的至少一跳过渡,形成形状异常。


图 3:通过正弦波生成异常样本的示例。 原始 𝐷𝑖𝑚2 = 0.5 · 𝐷𝑖𝑚1 + 1。在 shapelet 方面存在模式异常(A1-S:形状,A1C:相关性)、季节性 (A2) 和趋势 (A3)。 逐点异常包括全局异常 (A4) 和上下文异常 (A5).
3.4 Model Training Objective
最后通过投影 q i q_{i} qi和标签 y i y_{i} yi的计算得到损失。 受超球面分类(HSC)[4, 18]的启发,我们使用交叉熵损失作为训练目标。 投影仪 g θ g_{\theta} gθ 输出二维投影 Q = { q 1 , . . . , q i , . . . , q N } Q=\{q_1,...,q_i,...,q_N\} Q={q1,...,qi,...,qN},并且 𝑠𝑜 𝑓𝑡𝑚𝑎𝑥 将 q i q_{i} qi 映射到一对概率 [1 − p i p_{i} pi, p i p_{i} pi ],其中 p i p_{i} pi和 1 − p i p_{i} pi 分别代表异常和正常的概率。 我们使用 𝑠𝑜 𝑓𝑡𝑚𝑎𝑥 代替 𝑠𝑖𝑔𝑚𝑜𝑖𝑑 分别获得两个概率。 交叉熵损失定义为:

其中 y i y_{i} yi是Y中的标签。对于带有标签的训练集,Y包含领域专家注释的原始标签和伪异常样本对应的标签。 值得一提的是,我们的方法不要求训练集包含异常。 如表 3 所示,CutAddPaste 在 UCR、SWaT 和 WADI 上表现良好,所有这些都是没有异常的通用训练集。
在测试阶段,我们将子序列样本 X i X_{i} Xi 的概率 p i p_{i} pi 视为异常分数 S i S_{i} Si ∈ [0, 1]。 然后,我们使用以下标准来判断 X i X_{i} Xi是否可以归类为异常:

其中 𝜏 是预定义的阈值。 附录 A 概述了综合算法。
4 EVALUATION
在本节中,我们概述了实验设置、实施细节、主要结果、消融研究、可视化和超参数分析。 该代码可在 https://github 上获取。 com/ruiking04/CutAddPaste.com/ruiking04/CutAddPaste.
4.1 Experiment Setup
这部分介绍实验设置,包括数据集、评估指标和基线。
数据集。 根据[19],评估是在 AIOps、UCR、SWaT 和 WADI 数据集上进行的,避开了有缺陷的时间序列 AD 数据集,如 Numenta [20]、Yahoo [21]、NASA(SMAP 和 MSL)[10], 和SMD [22]。 数据集详细信息如下。
• AIOps [23] 包含来自知名互联网公司的维护良好的业务云关键绩效指标的 29 个单变量时间序列子数据集。 一些参考文献可能将其标识为“KPI”。与模式异常相比,它包含更多点状异常。 • UCR [19]包含跨越各个领域的 250 个单变量时间序列子数据集。每个子数据集仅包含 1 个异常 大多数异常部分是模式异常。 • SWAT [24] 包含来自安全水处理 (SWaT) 测试台的 51 个传感器在正常和受攻击行为模式下的多变量数据。 • WADI [25]。 ] 是 SWaT 的扩展,具有 123 个传感器和执行器。模式异常比 SwaT 上的异常更短。
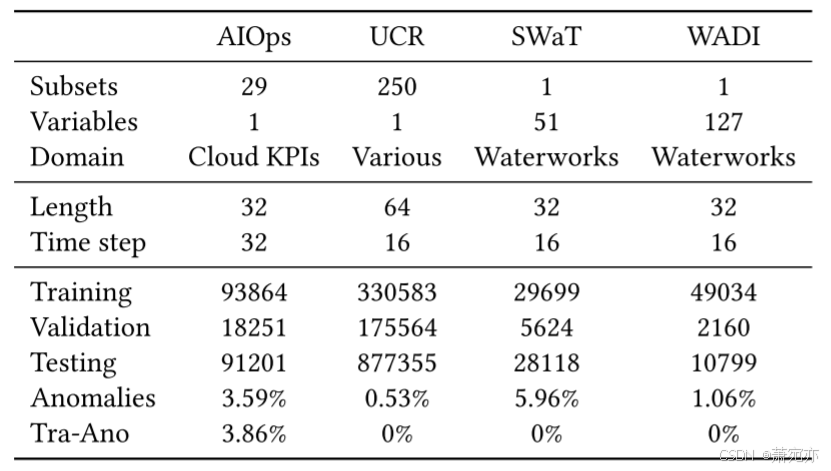
如表 2 所示,每个时间序列都使用具有时间步长 𝛿 的滑动窗口分割为长度 𝑡 序列。 该表还显示了训练、验证和测试集中的序列计数以及异常样本的比例。 指标。 目前,时间序列异常检测还没有统一的评估方案。 有些指标可能存在较高或较低的偏差,从而导致混乱的情况。 在本文中,我们将量化和比较几个众所周知的指标,并说明选择 RPA [10] 指标是为了公平起见的最佳选择。 由于常见的时间序列异常,尤其是模式异常,通常是连续的而不是孤立的点,传统的 PointWise (PW) 精度、召回率和 F1 分数计算往往会低估检测能力。 为了解决这个问题,人们提出了许多替代指标,例如 NAB 分数 [20] 和调整点 (PA) 指标 [11]。 然而,与 NAB 分数相比,PA 指标的计算更简单,因此被更广泛地接受。 如图 4 所示,PA 指标假设如果异常窗口中的任何点被识别为异常,则窗口中的所有点都被视为真阳性。 尽管如此,[10]、[26]和[27]相继批评PA有很大可能高估AD性能,因此分别提出了RPA、PA%K和隶属度指标。
表 2:TSAD 数据集摘要。 Tra-Ano 是训练集中异常的比例。
在重现[3]和[17]的结果时,发现隶属度指标也倾向于高估,甚至随机异常分数也可能导致较高的隶属度F1分数。 对于 PA%K 指标,K% 是预定义阈值。 如图4所示,当窗口中异常点的比例超过K%时,所有点都被认为是异常的。 因此,PW和PA是K为100和0的特殊情况。此外,为PA%K确定合适的K会导致时间复杂度增加。 RPA 指标将整个异常段视为单个样本,这与我们对异常数量的直觉一致。
在本研究中,我们选择 RPA F1 分数作为公平的评估。 为了更好地进行比较,我们还报告了 PA F1score 的结果。 请注意,本文报告了整个数据集的指标,这是每个子数据集的 RPA 或 PA F1 分数的加权平均值:

其中,𝑀 是子数据集的数量,𝐸 是整个数据集的异常段总数,𝑒𝑖 是第 𝑖 个子数据集的异常段数量。 请参阅附录 C 了解我们方法的性能以及其他指标下的基线。
基线。 将所提出的方法与以下传统的、基于正态假设和基于异常假设的 AD 方法进行比较。
传统 AD 基线。 采用五种常用的传统AD方法:一类支持向量机(OC-SVM)[28]、隔离森林(IF)[29]、鲁棒随机切割森林(RRCF)[30]、谱残差(SR)[31] ,和潮湿[32]。 受[26]的启发,我们设计了两个简单的基线:随机异常得分(RAS)和输入本身的绝对值作为异常得分(AAS)。 基于正态假设的 AD 基线。 然后,比较了三种基于单一和三种多重深度正态假设的 AD 方法:LSTM 编码器-解码器(LSTM-ED)[1]、Deep oneclass(Deep SVDD)[2]、Anomaly Transformer [33]、COCA [3] 、AOC [17] 和 TCC [16, 34]。
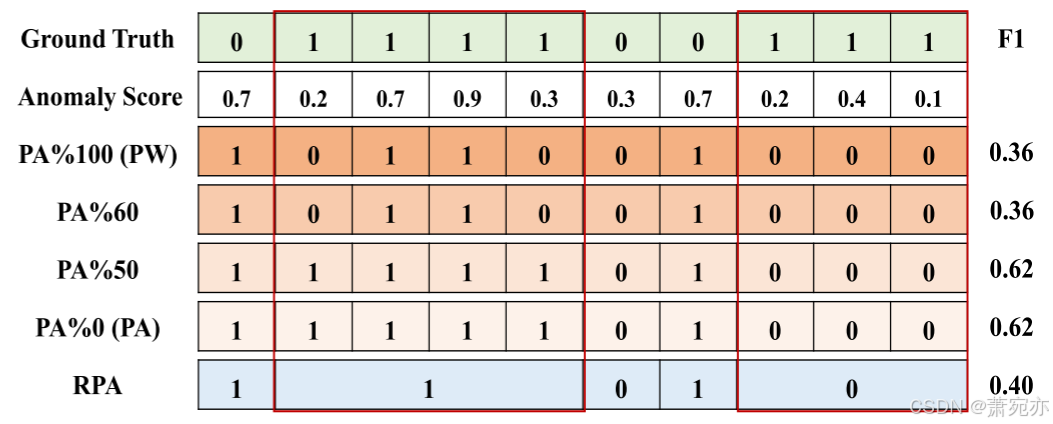
图 4:指标示意图。 红框是两个异常片段。 异常分数的阈值是0.5,决定每个点是正常(0)还是异常(1)。 右栏是每个指标得到的F1分数。
基于异常假设的 AD 基线。 最后,设置了一种基于异常假设的方法:NCAD [7]。 NCAD 为 KPI 数据集提供了监督和无监督设置,但前者可产生更好的 AD 性能,并作为本文的基准。 值得注意的是,虽然 Deep SVDD 是为图像数据中的 AD 设计的,但其基本概念仍然很重要。 因此,之前的工作 [3,7,17] 通过采用 Conv1D 来实现其自动编码器架构,使其适应时域。 关于基于[16]的TCC,我们在预训练阶段使用TS-TCC[34]进行表示学习,并在微调过程中根据Deep SVDD原理进行异常检测。
4.2 Implementation Details
TCN编码器的1D-CNN的dropout率为0.45。 我们在 Adam 优化器中采用从 1𝑒 − 4 到 5𝑒 − 4 的学习率,权重衰减为 5𝑒 − 4,𝛽1 = 0.9,𝛽2 = 0.99。 由于在UCR中,每个时间序列只有一个异常段,因此我们选择异常得分最大的样本作为异常所在的位置。 此外,我们在 UCR 上执行早期停止策略,因为来自不同域的时间序列在收敛时期有所不同。 对于其他数据集,获得的原始异常分数被转换为 Z 分数,我们根据 3𝜎 规则搜索最佳异常阈值𝜏 ∈ [−3, 3]。 为了确保稳健性,每种方法都使用不同的随机种子执行 10 次,以获得指标的平均值和标准差。 这些模型使用 PyTorch 1.7 和 Merlion 1.1.1 [35] 实现,并在 NVIDIA Tesla V100 GPU 上进行训练。 有关超参数的更多详细信息,请参阅附录 B。
4.3 Main Results
我们在表 3 中以 RPA 和 PA F1 形式报告了基线和我们的方法的 AD 性能。 指标选择。 我们设计了两个简单的基线作为比较目标,以强调选择公平指标的重要性:RAS 和 AAS。 RAS 生成随机小数作为几个时期的异常分数,然后选择最好的一个。 AAS 将归一化输入的绝对值视为异常分数。 它们检测异常的方式可能看起来很荒谬,但却收到了令人惊讶的结果,甚至击败了 SR 和 TCC 等几种经典方法。 这一观察结果与现有工作 [19, 26] 中的讨论非常一致,表明由于数据集的变化和评估指标的变化,最新的进展很可能会产生误导。 这种现象在 PA 指标下更为明显——RAS 和 AAS 的 F1 分数在 SWaT 上分别达到 83.55% 和 82.33%。 我们将这种高估归因于该数据集中长期序列(模式)异常的大部分。 在评估方法的性能时,PA 将异常段中的每个点视为异常。 然而,一旦遇到正确的预测点,它就会不合理地假设整个异常段的所有预测都是正确的。 因此,几乎所有这些方法在 SWaT 上的 PA F1 分数都超过 80%,几乎无法区分。 相比之下,对于AIOps等以点异常为主的数据集,PA相对公平,例如随机RAS为18.57%。 因此,考虑到异常类型影响指标的公平性,本文谨慎采用RPA作为指标,以下“F1score”均为RPA指标。我们进一步提倡使用RPA代替PA。 附录 C 中提供了 CutAddPaste 的性能和其他指标下的基线,而我们的方法仍然优于其他方法。
TSAD 性能。 从表3中的数据集来看,有以下两个关键观察结果。 首先,OC-SVM、AAS 和 COCA 等方法在 AIOps 和 UCR 数据集上的 AD 性能存在显着差异。 例如,COCA 的 RPA F1 分数在两个单变量数据集之间相差 16%。 这种差异可以归因于每个数据集中的主要异常类型:AIOps 的逐点异常和 UCR 的模式异常。 因此,这些方法对特定类型的异常表现出不同的敏感性。 相比之下,我们提出的方法有效地在这两种异常类型之间取得了相对平衡,如两个数据集上的 RPA F1 超过 68% 所示。 其次,如 SWaT 和 WADI 的结果所示,多变量 TSAD 更加棘手。 大多数方法无法匹配其在单变量数据集上显示的功能。 即使是针对多元数据设计的方法,例如 Anomaly Transformer,在 SWaT 上也只能达到 32.91%,并且随着维数的增加,在 WADI 上表现更差。 另一方面,Anomaly Transformer 在单变量数据集上表现不佳,这表明单变量和多变量 TSAD 任务有不同的侧重点。 我们的方法在 SWaT 和 WADI 上获得了 45.86% 和 26.58% 的 F1 分数,大大超过了 Anomaly Transformer,这表明 CutAddPaste 增强在进展中发挥了重要作用。
表 3:超过 10 次运行的平均 RPA F1 分数 (%) 和 PA F1 分数 (%),以及基线、我们的方法以及 AIOps、UCR、SWaT 和 WADI 数据集上的变体的标准差。 值得注意的是,PA 是我们不推荐的指标。 最好的结果以粗体显示。 SR 不支持多元时间序列异常检测。 SameCAP 是仅适用于多元时间序列的变体方法。
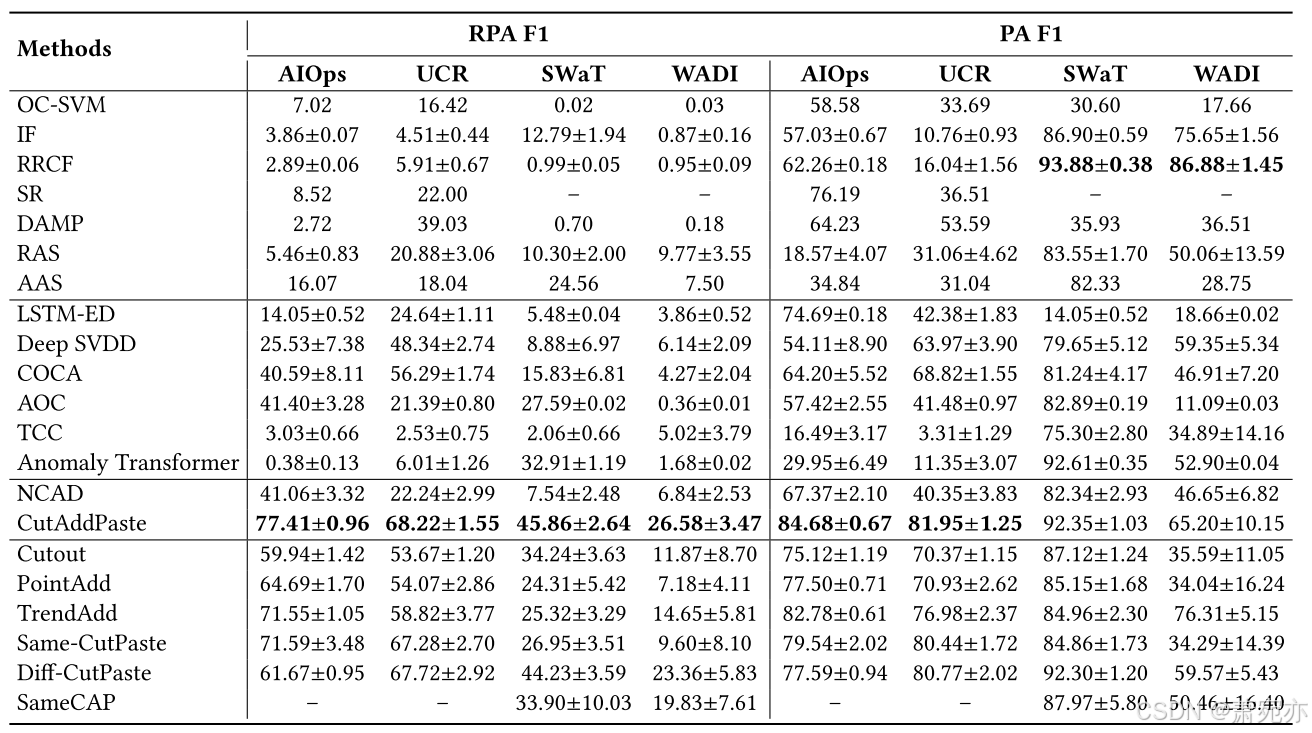
根据表中方法的比较,可以得出以下结论。 首先,在传统的机器学习方法中,DAMP和SR在UCR上获得了39.03%和22%的RPA F1,甚至超过了一些深度方法。 这表明浅层方法在某些特定情况下也可以很好地工作,例如单变量模式异常。 然而,它们在处理高维多元时间序列方面存在缺陷。 其次,基于 TSAD 的正态性假设,AOC 和 COCA 表现出比其他基线更好的性能。 这意味着涉及重建和合并多个正态性假设的技术更符合正态样本的性质。 此外,TCC 令人不满意的结果证实了预训练限制了两阶段方法能力的论点。 最后,比较基于异常假设的方法,NCAD 在所有四个数据集的异常检测中落后于 CutAddPaste。 在 AIOps 上,NCAD 成功实现了超过 41% 的可观 F1 分数,因为它生成了与数据集性质一致的逐点异常。 这再次证实了基于异常假设的 AD 方法作为一种有前途的途径的潜力。 然而,它与我们在其他数据集上的 CutAddPaste 的差距表明,点异常和 OE 的注入可能难以有效地处理复杂的模式异常。 总之,所提出的 CutAddPaste 方法成功地平衡了点异常和模式异常,生成了具有高度辨别力的异常分数,并在所有四个数据集上优于所有基线。 这一结果强调了基于 CutAddPaste 增强的 AD 的有效性和鲁棒性。
4.4 Ablation Study
在本节中,我们研究了六种变体,从仅剪切、添加、移植的CutPaste,到具有相同趋势的CutAddPaste。 这些变体在四个数据集上的 RPA 和 PA F1 分数如表 3 所示。结果揭示了我们提出的方法组件有效性的一些见解。 剪下。 该变体从样本𝑋𝑖中选择一个随机子序列,并将其上的值替换为零,以模拟补丁被切断。 看来纯掩蔽方法有助于提高性能,很可能是因为掩蔽消除了原始图案。 点加法和趋势加法。 这两种变体都直接在样本中添加异常。 PointAdd 在样本 𝑋𝑖 的随机位置注入异常点 𝑥𝑗 (|𝑥𝑗 − 𝜇| > 3𝜎),其中 𝜇 和 𝜎 是 𝑋𝑖 的平均值和标准差。 TrendAdd 保留了“添加”组件,该组件添加了一块趋势异常值,这些异常值显着改变了样本 𝑋𝑖 的平均值。 与 Cutout 相比,除了 AIOps 之外,PointAdd 对 AD 性能的改进几乎没有,这证实了仅逐点增强是不够的直觉。 即使在包含更多点异常的 AIOps 数据集上,TrendAdd 的表现也优于 PointAdd,这表明 Add 组件产生的异常既包括趋势异常,也包括逐点异常。 剪切粘贴变体。 Same-和Diff-CutPaste是我们实现的基于窗口的CutPaste方法。 对于要粘贴到样本 𝑋𝑖 的补丁,前者从 𝑋𝑖 本身剪切它,而后者从另一个 𝑋𝑗 剪切它。 它们都优于剪切变体,证明了粘贴组件的重要性。 Diff-CutPaste 比 Same-CutPaste 产生更好的结果,这表明从不同样本中提取可以增强模型对异常实例的暴露,从而提高性能和鲁棒性。 同时,Diff-CutPaste 与 CutAddPaste 之间的差距再次凸显了 Add 术语在我们的方法中的重要性。 CutAddPaste 具有相同的趋势(SameCAP)。 我们进一步研究了补丁中添加的不同趋势的影响。 SameCAP 在补丁的每个维度上添加相同的趋势,在每个多变量数据集上,它的性能比 CutAddPaste 低 7% 以上。 这表明不同趋势引入的相关异常起作用

图 5:AIOps 和 UCR 数据集上的 CutAddPaste AD 结果的可视化。 标题是它们的编号(数据集中的 ID),x 轴是时间戳,y 轴是信号值。 原始数据显示为蓝色曲线。 黄色区域是真实异常,包括点和模式异常。 红色曲线代表我们的方法预测的异常分数。
总体而言,CutAddPaste 优于其他六种替代方案,表明我们方法中每个组件的有效性和重要性。
4.5 可视化
为了提供更直观的评估,我们的方法在 AIOps 和 UCR 数据集上进行了可视化,如图 5 所示。定性分析表明,该模型预测了一系列具有更好区分度的异常分数,即,它对每种类型的异常分数更加敏感。 异常。 在代表 AIOps 数据集的图 5(a) 中,时间序列包含几个不同的逐点异常,使得异常检测相对简单。 我们的 CutAddPaste 方法生成的高异常分数与真实异常区域紧密一致,证实我们的方法对逐点异常敏感。 另一方面,图 5(b) 描绘了 UCR 数据集中的时间序列,每个序列仅包含一个微妙的模式异常片段。 由于这些类型的异常不明显,因此通常更难检测。 尽管面临挑战,我们的方法的异常分数在真实异常区域周围急剧达到峰值,有效地识别了异常。 虽然该模型确实产生了一些其他高分部分,但整体性能令人印象深刻。 简而言之,CutAddPaste 在两个子序列上都表现良好,进一步说明我们的模型可以检测简单的逐点异常和复杂的模式异常。 另外,为了进一步分析生成的伪异常与原始时间序列之间的差异,其t-SNE嵌入如图6所示。总体而言,伪异常和正常样本被划分为相对清晰的决策边界,如图6所示 如图6(a)、6©和6(d)所示。 在图6(b)中,尽管我们的模型在UCR数据集上生成的伪异常与正常样本有些混合,但大多数都超出了正常样本的范围。 同时,一些伪异常分散在原始异常附近,这表明 CutAddPaste 可以帮助异常检测器泛化到未见的异常分布,并在其上表现良好,尤其是在 AIOps 上。

图 6:四个数据集上原始样本和生成样本的 t-SNE 嵌入的图示。 顶部标题是数据集名称和数据集中的 ID,其中 © 和 (d) 不包含 ID,因为 SWaT 和 WADI 只有一个子集。 蓝点是正常样本,红色是异常样本,绿色是 CutAddPaste 生成的伪异常样本。
4.6 Hyperparameters Analysis
我们进行了敏感性分析来研究超参数的影响,包括趋势项的程度 (𝜌) 和补丁的最小长度 (𝜁),如图 7 所示。y 轴代表 RPA F1 分数。 总的来说,我们的模型对 𝜌 和 𝜁 更敏感。 对于𝜌的分析,我们主要考虑AIOps数据集,该数据集主要包含逐点异常,因此受趋势项比例的影响很大。 如图7(a)所示,很明显,在一定范围内,增加趋势项的程度可以增强模型对点异常的敏感度,从而提高异常检测性能。 然而,超过某个点,较大的 𝜌 可能会损害性能,可能是因为它导致模型过度关注生成的极值点。 我们观察到 𝜌 = 1 表现最好。 图 7(b) 显示了在 2 到 20 范围内变化 𝜁 的结果。该图表明,当最小长度 𝜁 设置为 10 时,模型在 SWaT 数据集上表现最佳。这强调了保持平衡的重要性 粘贴(目标)样本 𝑋𝑖 和剪切(源)样本 𝑋𝑗 的长度之间的差异,以实现最佳的异常检测性能。 更多超参数的分析可以参见附录D。

图 7:AIOps 和 SwaT 数据集的两个敏感性分析实验。 左边是趋势项𝜌的度数,右边是面片𝜁的最小长度。
5 CONCLUSION
我们提出了 CutAddPaste,一种基于异常知识的方法,致力于时间序列异常检测。 据我们所知,它提供了一个简单而强大的增强功能,这是第一个实现将模型暴露于所有五种 TS 异常(包括多元数据中的相关异常)的增强功能。 通过整合领域知识,CutAddPaste 使模型能够理解和检测各种异常并提高整体性能。 我们的方法在四个现实世界数据集上展示了卓越的功能。 它强调了将模型暴露于多种类型异常的有效性,即使是粗略的近似。 我们设想 CutAddPaste 增强可以作为未来强大的时间序列异常检测模型的基础。 此外,我们提倡在 TSAD 中采用 RPA 等公平的评估指标,这对于凝聚共识并为未来的模型创新奠定基础至关重要。 没有它,所取得的令人印象深刻的成果可能仍然是一种幻想。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








