04求指定点到图中各点最短距离——Dijkstra算法

04基于Dijkstra算法的单源最短路径

1.问题

给定一有向图G = <V, E> ，其中V为G的顶点集，E为G的边集，<u, v> 代表从顶点 u 到顶点 v 的有向边，w<u, v> 代表此有向边的权重。

给定一点 u1 ∈ V，如何得到该点到图中各顶点的最短距离？

2.解析

Dijkstra算法的基本思想

Dijkstra算法的基本思想：

1. G = <V, E>，初始时令 dis={V_u}（V_u为选中的起始点，V_u∈V）,T=V-dis={其余顶点}，T中顶点对应<V_u,V_i>的距离值若存在，d(V0,Vi)为<V0,Vi>边上的权值；若不存在<V_u,V_i>，d(V0,Vi)为∞（下文代码用INIT表示极大数）。
2. 从T中选取一个与S中顶点有关联边且权值最小的顶点V_temp，加入到S中。
3. 对其余T中顶点的距离值进行修改：若将V_temp作为中转顶点，从V_u到V_i的距离值缩短，则修改此距离值。重复上述步骤2、3，直到S中包含G中所有顶点，即 S=V，T=Ø 为止。

举个栗子

给定一有8顶点的有向图G = <V, E> ，顶点和边的对应关系及各边权重如下图所示：

我们以点V_a为起始点为例。

• 初始情形1：S={V_a}, T={V_b,V_c,V_d,V_e,V_f,V_g,V_h},
  dis[]={0,1,∞,∞,∞,∞,∞,∞}.

然后在dis[]中，选择距V_a最短且在T的点V_temp，将它从T移除并加入S。然后，松弛T其余各点，若这些点到V_a的距离大于经过点V_temp中转的距离，则更新dis[]中点V_a到点V_temp的距离。

接着，继续在dis[]中选择距V_a最短且在T的点V_temp1，重复上述步骤，直至S=V。（后文不再赘述）

• 情形2：加入V_b。S={V_a,V_b}, T={V_c,V_d,V_e,V_f,V_g,V_h},
  dis[]={0,1,∞,3,∞,∞,∞,∞}.
  
• 情形3：加入V_d。S={V_a,V_b,V_d}, T={V_c,V_e,V_f,V_g,V_h},
  dis[]={0,1,4,3,∞,11,∞,∞}.
  
• 情形4：加入V_c。S={V_a,V_b,V_d,V_c}, T={V_e,V_f,V_g,V_h},
  dis[]={0,1,4,3,∞,11,∞,∞}.
  
• 情形5：加入V_f。S={V_a,V_b,V_d,V_c,V_f}, T={V_e,V_g,V_h},
  dis[]={0,1,4,3,13,11,∞,∞}.
  
• 情形6：加入V_e。S={V_a,V_b,V_d,V_c,V_f,V_e}, T={V_g,V_h},
  dis[]={0,1,4,3,13,11,15,∞}.
  
• 情形7：加入V_g。S={V_a,V_b,V_d,V_c,V_f,V_e,V_g}, T={V_h},
  dis[]={0,1,4,3,13,11,15,18}.
  
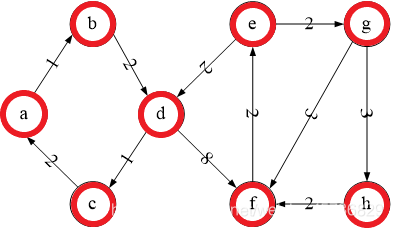
• 最后情形8：加入V_h。S={V_a,V_b,V_d,V_c,V_f,V_e,V_g,V_h}, T={},
  dis[]={0,1,4,3,13,11,15,18}.

至此，Dijkstra算法结束。

3.设计

unsigned int*  Dijkstra(int u, unsigned int mat[][N]) {	//点u为起始点

	unsigned int min,temp,visited[N] = { 0 };	
	//visited[i]数组记录点i是否已找到距离u的最短距离，0未确定，1确定
	unsigned int* dis = (unsigned int*)malloc(sizeof(unsigned int) * N);	//点u到其他点的距离数组
	visited[u] = 1;		
	for (i from 0 to N-1) {
		//根据矩阵初始化起点u到其他点的直接距离
	}	

	for (k from 1 to N) {		//逐一确定剩余N-1个点
		min = INIT; temp = 0;
		for ( i from 0 to N-1) {
			//每次选择距u最短且未被确定过的点加入,将该点下标赋给temp
		}
		visited[temp] = 1;	
		//松弛
		for ( i from 0 to N-1) {
			//更新以temp为中转点的最短距离
		}
	}
	return dis;	//返回最短距离数组
}

4.分析

核心代码块部分大循环里套了两个平行的小循环，其复杂度为：Dijkstra()=O(n²).

进一步分析，若给定有向图的边数相对较少，我们可以改用稀疏矩阵来存储图的相关信息，调整代码，以减少循环的次数，提升程序运行效率。

5.源码

https://github.com/KabgRs/F-SDDR/tree/%E7%AE%97%E6%B3%95%E5%88%86%E6%9E%90%E4%B8%8E%E8%AE%BE%E8%AE%A1%E4%BD%9C%E4%B8%9A/04%E6%B1%82%E6%8C%87%E5%AE%9A%E7%82%B9%E5%88%B0%E5%9B%BE%E4%B8%AD%E5%90%84%E7%82%B9%E6%9C%80%E7%9F%AD%E8%B7%9D%E7%A6%BB_Dijkstra%E7%AE%97%E6%B3%95
（在搜索框复制源码链接后注意删掉“原创声明”）