2.矩阵
2.1 矩阵的定义
矩阵:由
m
×
n
m\times n
m×n个数按照一定的次序排列成的m行n列的矩形数表称为
m
×
n
m\times n
m×n的矩阵,简称矩阵。
A
=
[
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋯
⋯
⋯
⋯
a
m
1
a
m
2
⋯
a
m
n
]
,简记为
A
=
(
a
i
j
)
m
×
n
A=\begin{bmatrix}a_{11}&a_{12}&\cdots & a_{1n}\\ a_{21}&a_{22}&\cdots & a_{2n}\\ \cdots&\cdots&\cdots&\cdots\\ a_{m1}&a_{m2}&\cdots & a_{mn} \end{bmatrix},简记为A=(a_{ij})_{m\times n}
A=⎣
⎡a11a21⋯am1a12a22⋯am2⋯⋯⋯⋯a1na2n⋯amn⎦
⎤,简记为A=(aij)m×n
- 行矩阵:只有一行;
- 列矩阵:只有一列
特殊的矩阵:
-
当m==n时,即矩阵的行数与列数相等时,称矩阵为方阵。
- 主对角线:行标 == 列表
- 斜对角线:行标 + 列表 == n
只有方阵才有主对角线和斜对角线
-
零矩阵
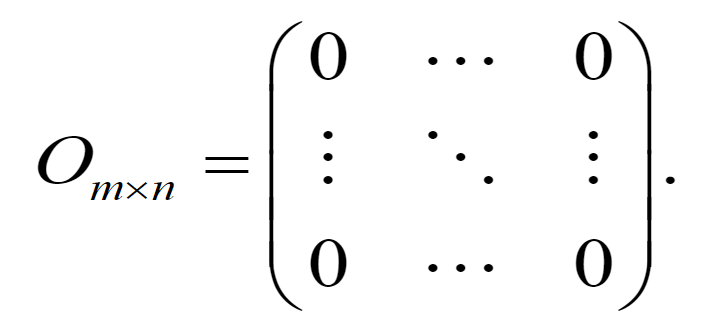
-
对角矩阵
一定是方阵

-
单位阵E
因为对角阵一定是方阵,所以只要一个角标就能确定维度
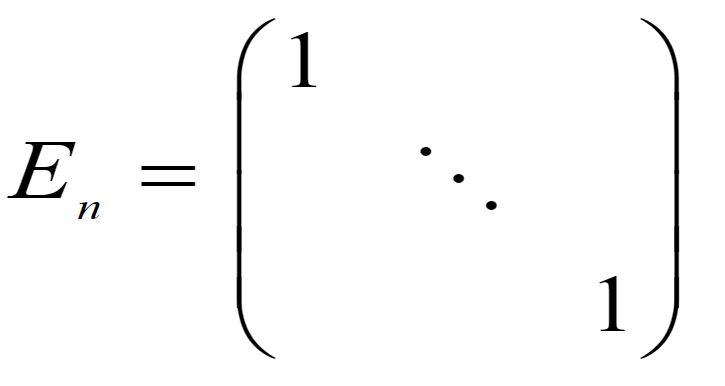
-
数量阵
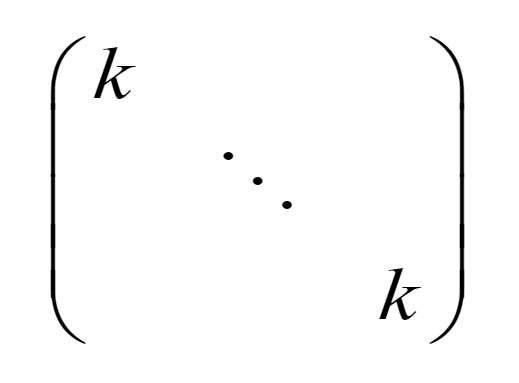
-
-
三角阵
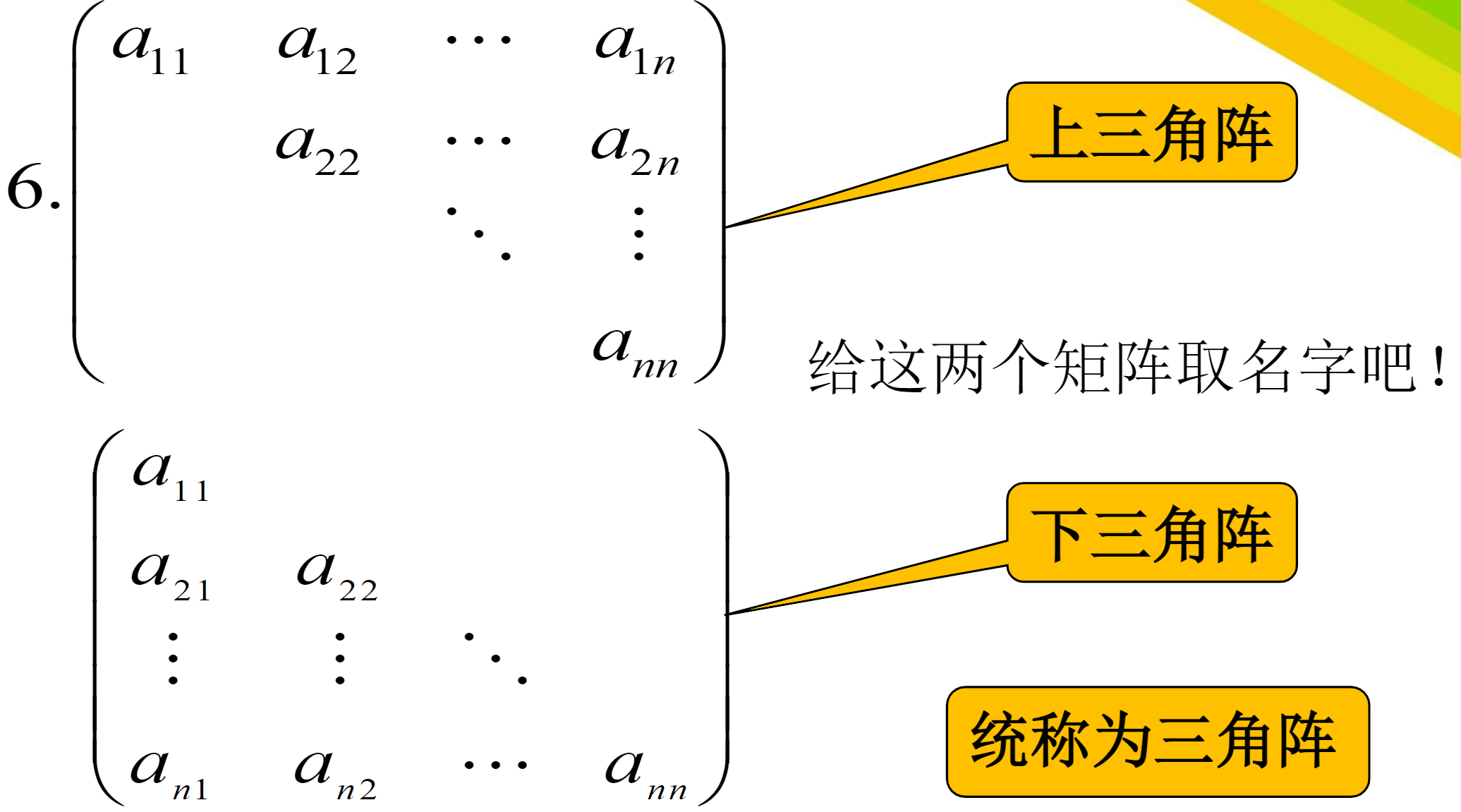
- 上三角阵
- 下三角阵
-
梯形阵
重要矩阵
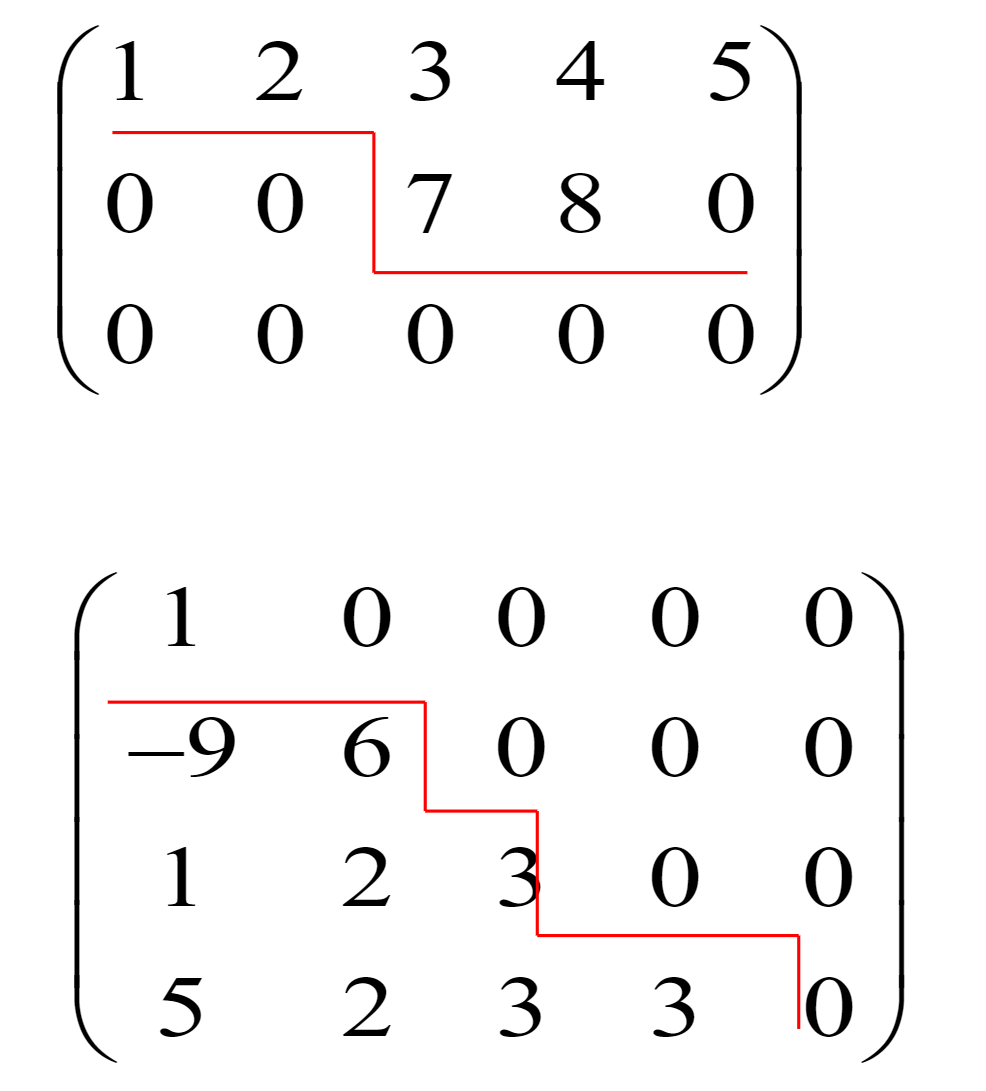
2.2 矩阵的运算
2.2.1 线性运算
2.2.1.1 相等
矩阵相等:两个矩阵相等是指这两个矩阵有相同的行数与列数,且对应元素相等
- 同型、对应元素相等
2.2.1.2 加减法
对应元素相加、相减
运算规律:
- 交换律: A + B = B + A A+B=B+A A+B=B+A
- 结合律: ( A + B ) + C = A + ( B + C ) (A+B)+C = A+(B+C) (A+B)+C=A+(B+C)
- 零元: A + O = A = O + A , A − A = O A+O=A=O+A,A-A=O A+O=A=O+A,A−A=O
负矩阵:每个元素都取负—— − A = ( − a i j ) m × n -A = (-a_{ij})_{m\times n} −A=(−aij)m×n
2.2.1.3 数乘


2.2.2 矩阵的乘法
2.2.2.1 矩阵乘法的计算
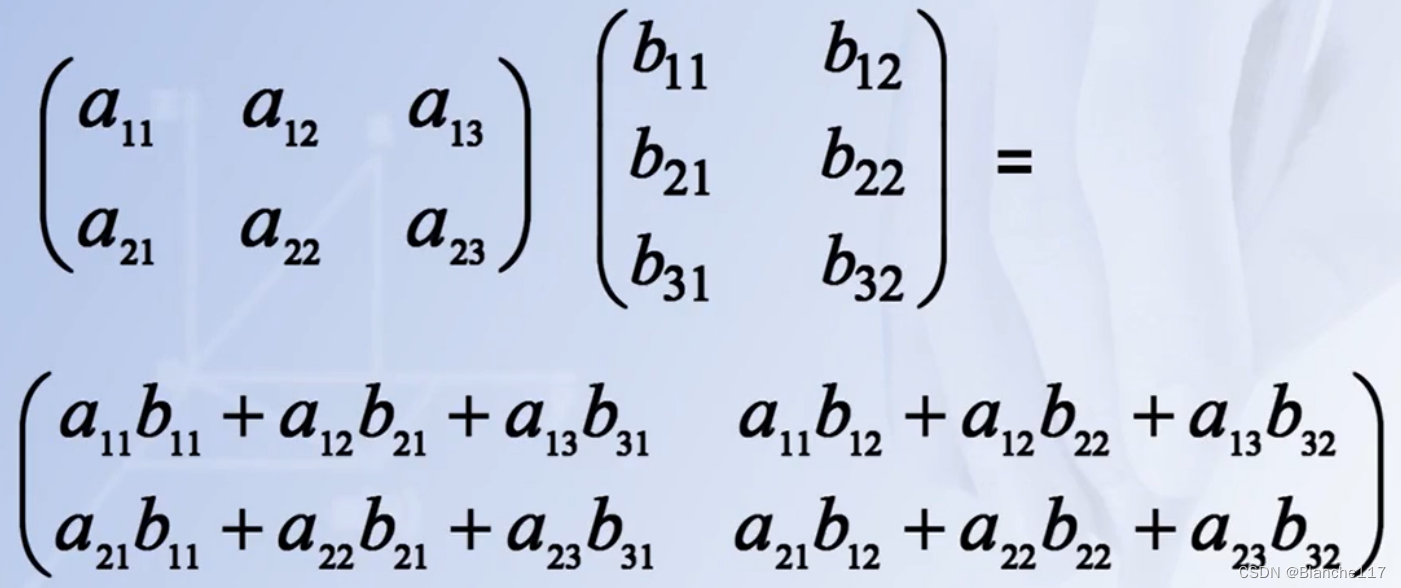
2.2.2.2 矩阵乘法满足的性质
矩阵乘法的特征:
- 矩阵乘法不满足交换律 A B ≠ B A AB\neq BA AB=BA
- 矩阵乘法不满足消去律
- A B = 0 AB=0 AB=0不一定A=0或B=0,可以是非零的因子
由于不满足上述的性质,所以矩阵的乘法对于完全平方等公式不成立。

满足的运算规律:
-
结合律: ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
-
分配律: A ( B + C ) = A B + A C A(B+C) = AB+AC A(B+C)=AB+AC
( B + C ) A = B A + C A (B+C)A = BA+CA (B+C)A=BA+CA
-
k ( A B ) = ( k A ) B = A ( k B ) k(AB) = (kA)B=A(kB) k(AB)=(kA)B=A(kB)
-
E m A m × n = A = A m × n E n E_mA_{m\times n} = A = A_{m\times n}E_n EmAm×n=A=Am×nEn
2.2.2.3 方阵的正整数幂
方阵的幂的定义: A k = A A A . . . A A^k=AAA...A Ak=AAA...A,特别的,当 A ≠ 0 A\neq 0 A=0时, A 0 = E A^0=E A0=E
-
A k + l = A k A l A^{k+l} = A^kA^l Ak+l=AkAl
-
( A B ) k ≠ A k B k (AB)^k \neq A^kB^k (AB)k=AkBk
( A B ) k = A B A B A B A . . . A B (AB)^k = ABABABA...AB (AB)k=ABABABA...AB
A k B k = A A A A A . . A B . . . . B B B A^kB^k = AAAAA..AB....BBB AkBk=AAAAA..AB....BBB
若满足 A B = B A AB=BA AB=BA,那么上式相等
2.2.3矩阵的转置
2.2.3.1 转置的概念
矩阵A的第i行转换为第i列,那么结果为 A T A^T AT
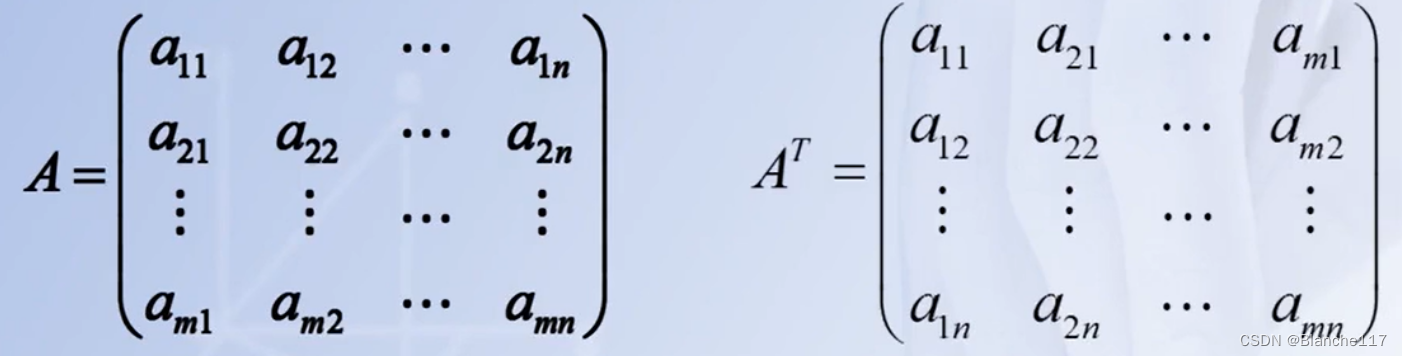
特别的,对角阵的转置为其本身
运算规律:
- ( A T ) T = A (A^T)^T=A (AT)T=A
- ( A + B ) T = A T + B T (A+B)^T=A^T+B^T (A+B)T=AT+BT
- ( k A ) T = k A T (kA)^T = kA^T (kA)T=kAT
- ( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT
证明:
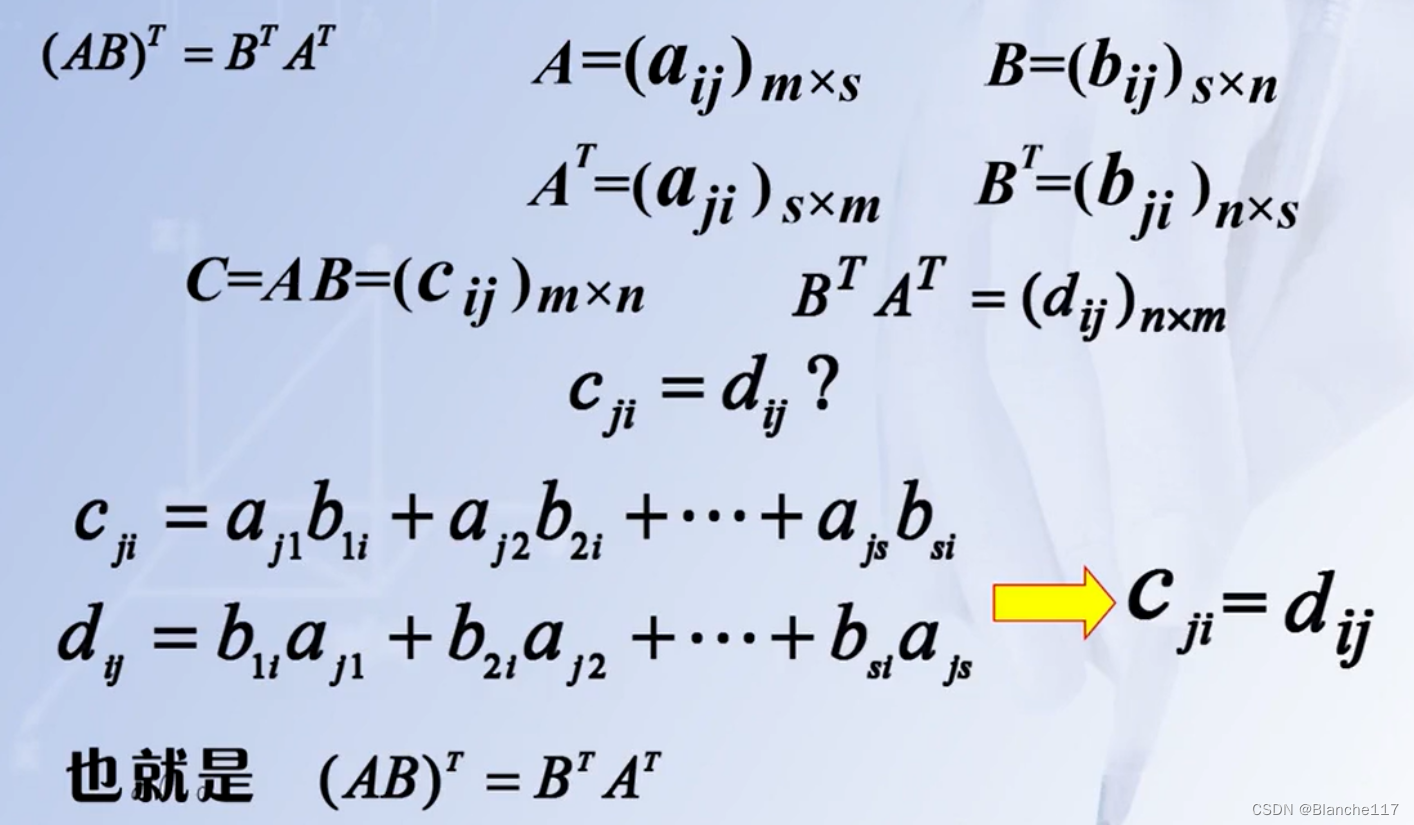
2.2.3.2 对称阵与非对称阵
对称阵与非对称阵一定是方阵
对称阵: A T = A A^T=A AT=A
对称阵的例子: A A T , A T A , A + A T AA^T,A^TA,A+A^T AAT,ATA,A+AT
反对称阵: A T = − A A^T=-A AT=−A
反对称阵的例子: A − A T A-A^T A−AT
任何一个矩阵都可以写成一个对称阵和一个反对称阵的和:
A = A + A T 2 + A − A T 2 A=\frac{A+A^T}{2}+\frac{A-A^T}{2} A=2A+AT+2A−AT
反对称阵: A T = − A A^T=-A AT=−A怎么说明 a i i = 0 a_{ii}=0 aii=0
2.2.4 方阵的行列式
2.2.4.1 定义
定义:由方阵A构成的行列式称为方阵的行列式,记为 ∣ A ∣ = d e t A |A|=det\ A ∣A∣=det A
只有方阵才有行列式!
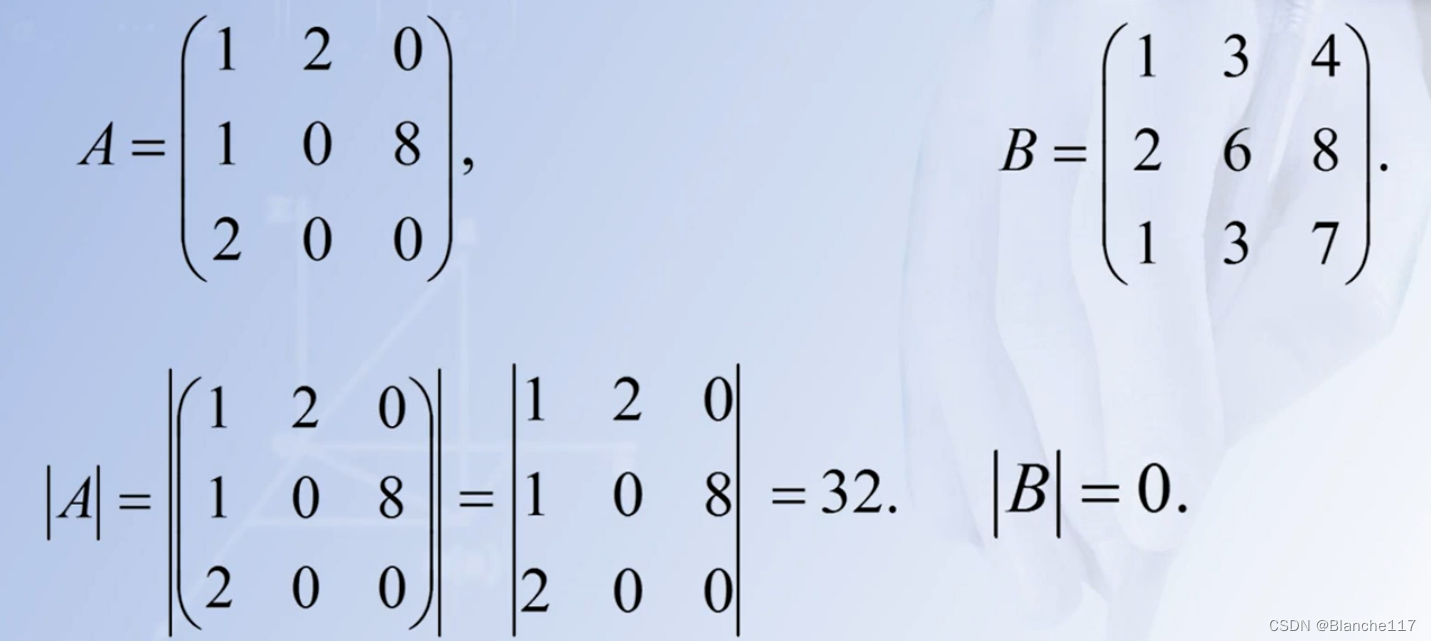

2.2.4.2 奇异方阵与非奇异方阵
定义:若方阵的行列式不为0,那么称方阵为非奇异方阵,否则称为奇异方阵。
- 0矩阵一定是奇异矩阵
- 单位阵是非奇异矩阵
2.2.4.3 方阵行列式的性质
由方阵A多确定的行列式除了具备行列式一般具有的性质外,还具有以下的性质:
设A,B为n阶方阵,k为常数,则有:
- ∣ k A ∣ = k n ∣ A ∣ |kA| = k^n|A| ∣kA∣=kn∣A∣
- ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣AB∣=∣A∣∣B∣,如果A,B不是方阵,那么不成立——只有方阵才有行列式
证明:奇数阶反对称阵的行列式为0
2.2.5 伴随矩阵
注意排列的顺序!!!

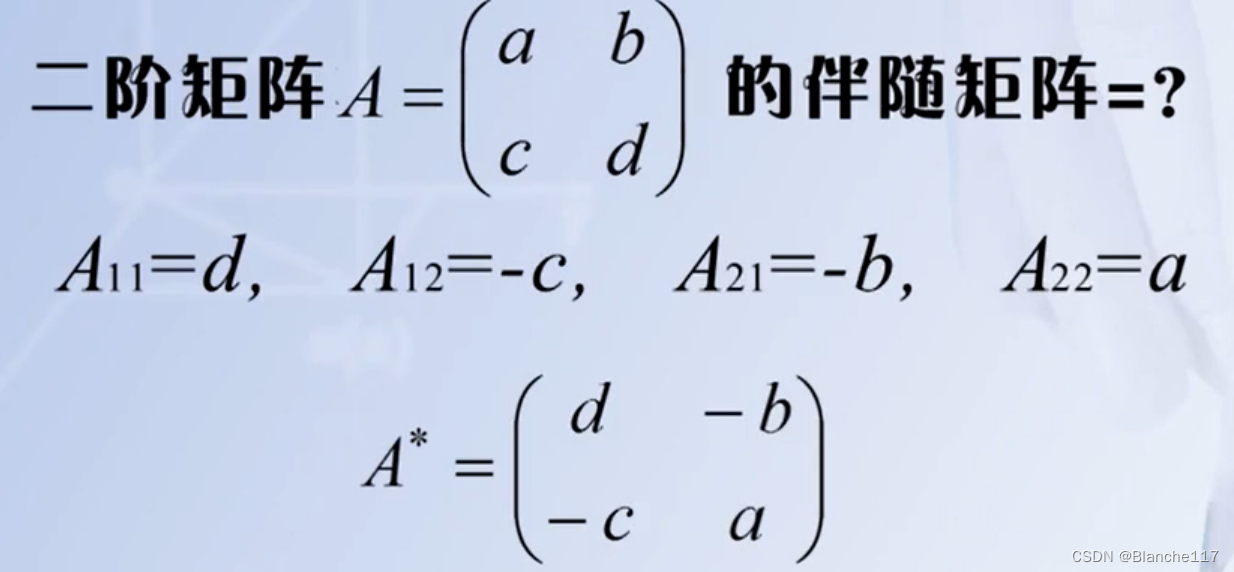
复习:
a
j
1
A
i
1
+
a
j
2
A
i
2
+
.
.
.
+
a
j
n
A
i
n
=
{
D
,
(
i
=
j
)
0
,
(
i
≠
j
)
a_{j1}A_{i1}+a_{j2}A_{i2}+...+a_{jn}A_{in}=\begin{cases}D,(i = j)\\ 0,(i\neq j)\end{cases}
aj1Ai1+aj2Ai2+...+ajnAin={D,(i=j)0,(i=j)
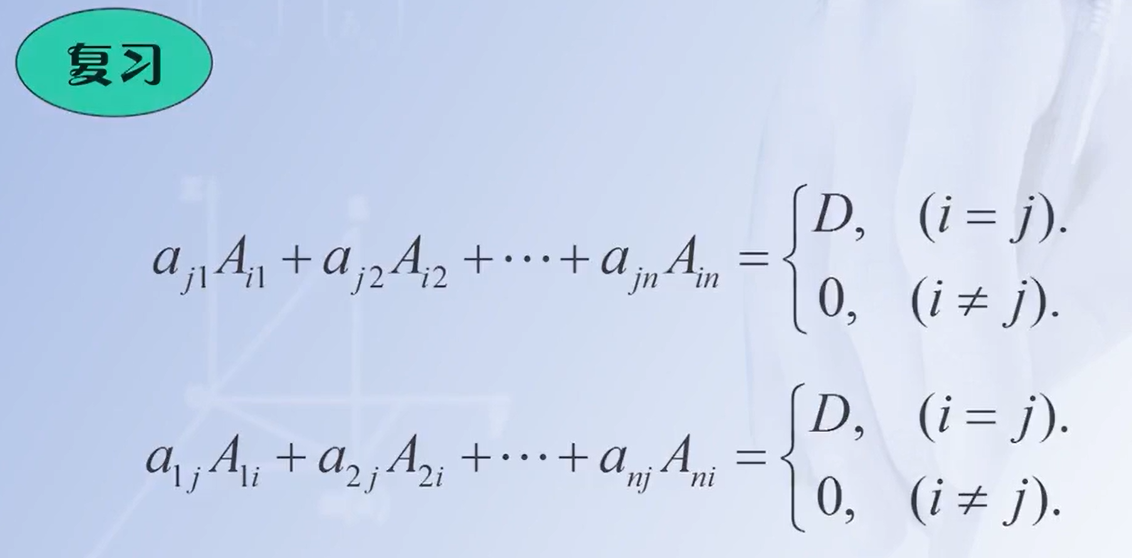
那么有:


important:
A
A
∗
=
A
∗
A
=
∣
A
∣
E
AA^*=A^*A=|A|E
AA∗=A∗A=∣A∣E
2.3 初等变换
2.3.1 矩阵初等变换的定义
以下三种变换称为矩阵的第一、二、三种初等变换:
- 对换矩阵中的第i, j两行(列)的位置,记做 r i j ( c i j ) r_{ij}(c_{ij}) rij(cij)或 r i ( c i ) ↔ r j ( c j ) r_i(c_i) \leftrightarrow r_j(c_j) ri(ci)↔rj(cj)
- 用非零常数k乘以第i行(列),记做 k r i ( k c i ) kr_i(kc_i) kri(kci)
- 将矩阵的第j行(列)乘以常数k后加到第i行(列)对应元素上去,记做 r i + k r j ( c i + k c j ) . r_i+kr_j(c_i+kc_j). ri+krj(ci+kcj).
初等行变换和初等列变换是线性代数中的重要工具,统称为初等变换。
初等变换的作用:
矩阵的初等变换可以将矩阵化为梯形阵。
初等变换后矩阵之间不相等:利用初等变换将A化为B,A与B之间用记号 → \rightarrow →或者 ≅ \cong ≅连接。
2.3.2 矩阵的等价
2.3.1 等价的定义
对矩阵A实行有限次初等变换得到矩阵B,则称A与B等价,记做 A ≅ B A\cong B A≅B或者 A → B A\rightarrow B A→B
等价的性质:
等价矩阵具有自反性,对称性,传递性
- 自反性: A ≅ A A\cong A A≅A
- 传递性: A ≅ B A \cong B A≅B, B ≅ A B\cong A B≅A
- 传递性: A ≅ B , B ≅ C ⇒ A ≅ C A\cong B, B\cong C\Rightarrow A\cong C A≅B,B≅C⇒A≅C
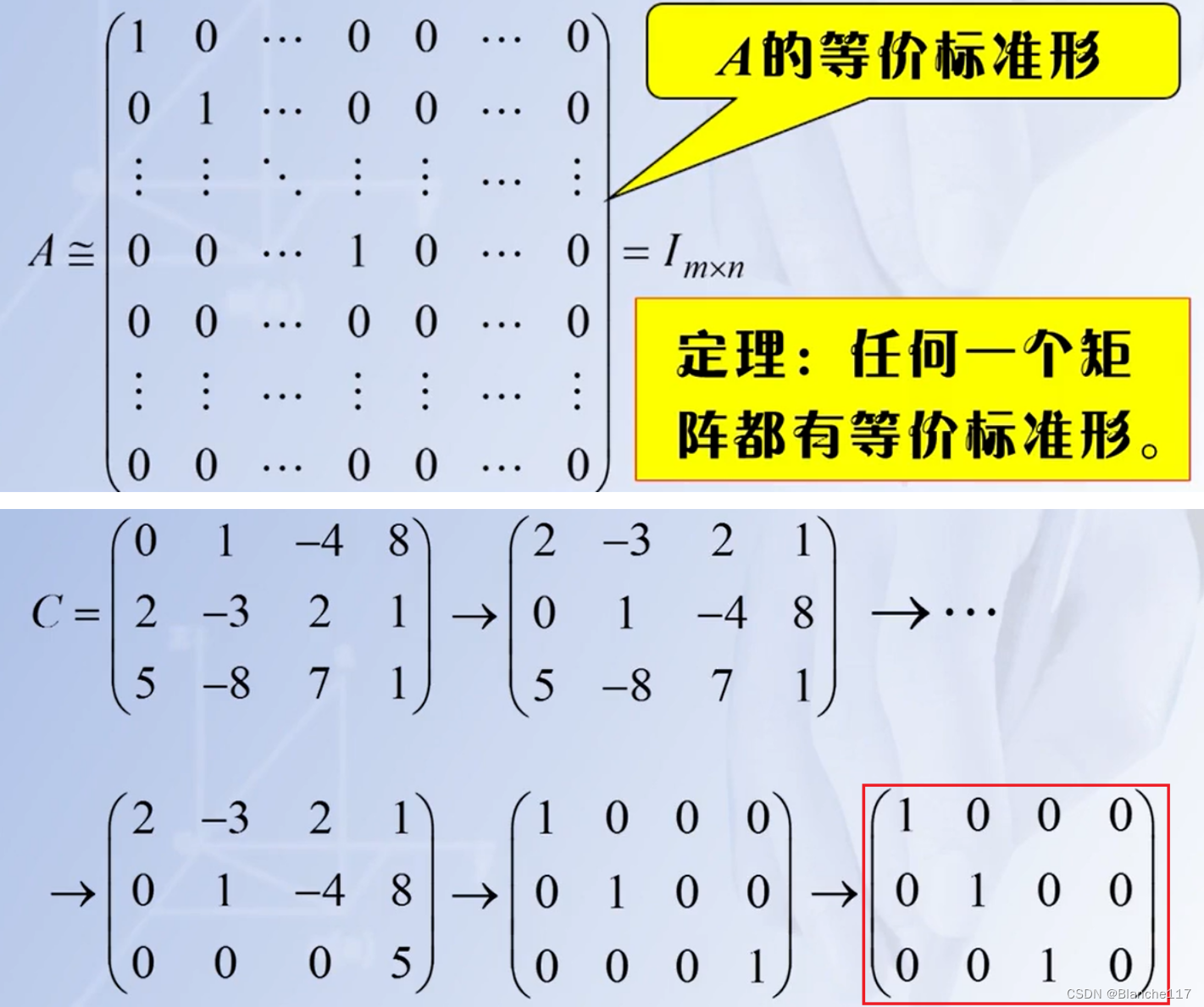
等价标准型中1的个数与什么有关?
2.4 矩阵的秩
2.4.1 矩阵秩的概念
k阶子式:在 A m × n A_{m\times n} Am×n中任取k行k列,位于这些行、列相交处的 k 2 k^2 k2个元素,按原次序组成的k阶行列式,称为矩阵A的k阶子式。
一般的:
m
×
n
矩阵的
k
阶子式有
C
m
k
C
n
k
个
m\times n矩阵的k阶子式有C_m^kC_n^k个
m×n矩阵的k阶子式有CmkCnk个
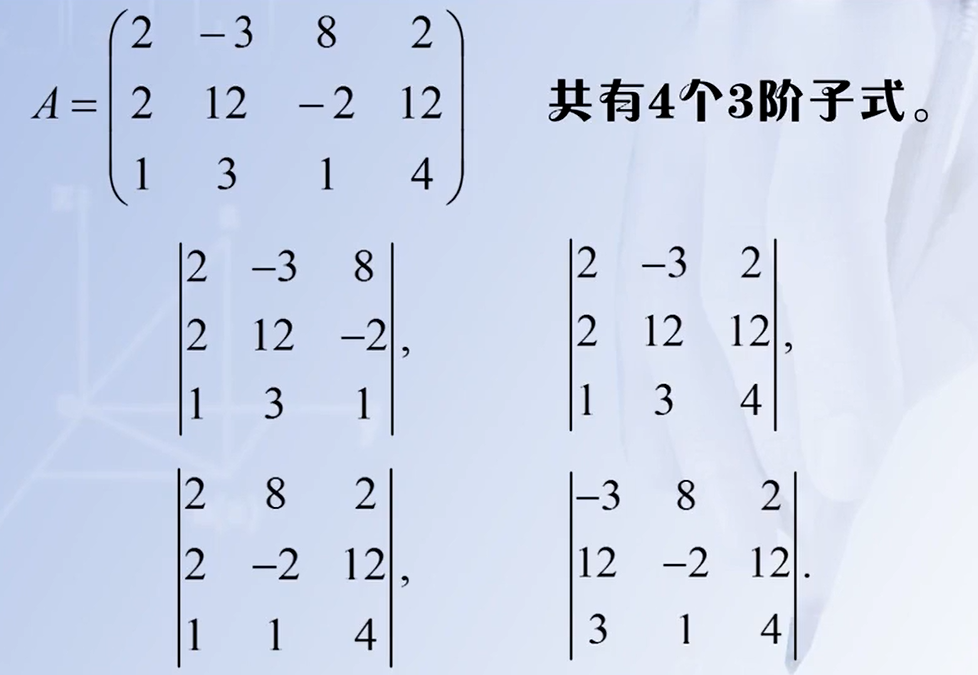
矩阵的秩rank:**矩阵的所有不为0子式的最高阶数称为矩阵的秩,**记做 r ( A ) r(A) r(A)
显然: r ( O ) = 0 ; r(O)=0; r(O)=0;只要A不是零矩阵,就有 r ( A ) > 0 r(A)>0 r(A)>0,并且:
(i) r ( A m × n ) < m i n { m , n } r(A_{m\times n})<min\{m,n\} r(Am×n)<min{m,n}
(ii)若有一个r阶子式不为0,那么 r ( A ) ≥ r r(A)\geq r r(A)≥r,
若所有的r阶子式全为0,那么 r ( A ) < r r(A)<r r(A)<r
(iii) r ( A T ) = r ( A ) r(A^T) = r(A) r(AT)=r(A)
(iv)设 A n × n , 若 ∣ A ∣ ≠ 0 , 则 r ( A ) = n ; 若 ∣ A ∣ = 0 , 则 r ( A ) < n A_{n\times n},若|A|\neq 0,则r(A) = n;若|A|=0,则r(A)<n An×n,若∣A∣=0,则r(A)=n;若∣A∣=0,则r(A)<n
2.4.2 秩的求法
梯形阵的秩很好求:非0行的行数
任何一个矩阵都可以通过初等变换将其转换为梯形阵

那么矩阵经初等变换后,其秩若不变,那么就可以根据初等变换求秩。
定理:矩阵经初等变换后其秩不变。
秩的求法:初等变换法
先做初等变换:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gzq9mTQi-1660358044153)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220724223603588.png)]](https://img-blog.csdnimg.cn/f437ffccfa914a68a1393583ffb6d526.png)
2.4.3 性质
若两个矩阵有相同的秩,那么这两个矩阵有相同的标准型,从而等价。
反之,如果两个矩阵等价,那么他们的秩相同。
定理:矩阵A和B等价的充要条件是 r ( A ) = r ( B ) r(A)=r(B) r(A)=r(B)
2.4.4 满秩矩阵
定义:如果方阵A的秩与其阶数相等,那么则称A为满秩矩阵,否则称为降秩矩阵。
定理:设A为满秩矩阵,那么A的标准型为同阶单位阵E。即:
A
≅
E
A\cong E
A≅E
定义:若方阵A的行列式
∣
A
∣
≠
0
|A|\neq 0
∣A∣=0,则A为非奇异矩阵;若
∣
A
∣
=
0
|A|=0
∣A∣=0,则称A为奇异矩阵。那么:
满秩
⇔
非奇异矩阵
降秩
⇔
奇异矩阵
满秩\Leftrightarrow非奇异矩阵\\降秩\Leftrightarrow 奇异矩阵
满秩⇔非奇异矩阵降秩⇔奇异矩阵
2.5 初等矩阵
2.5.1 定义与性质
定义:对单位阵进行一次初等变换后得到的矩阵称为初等矩阵。
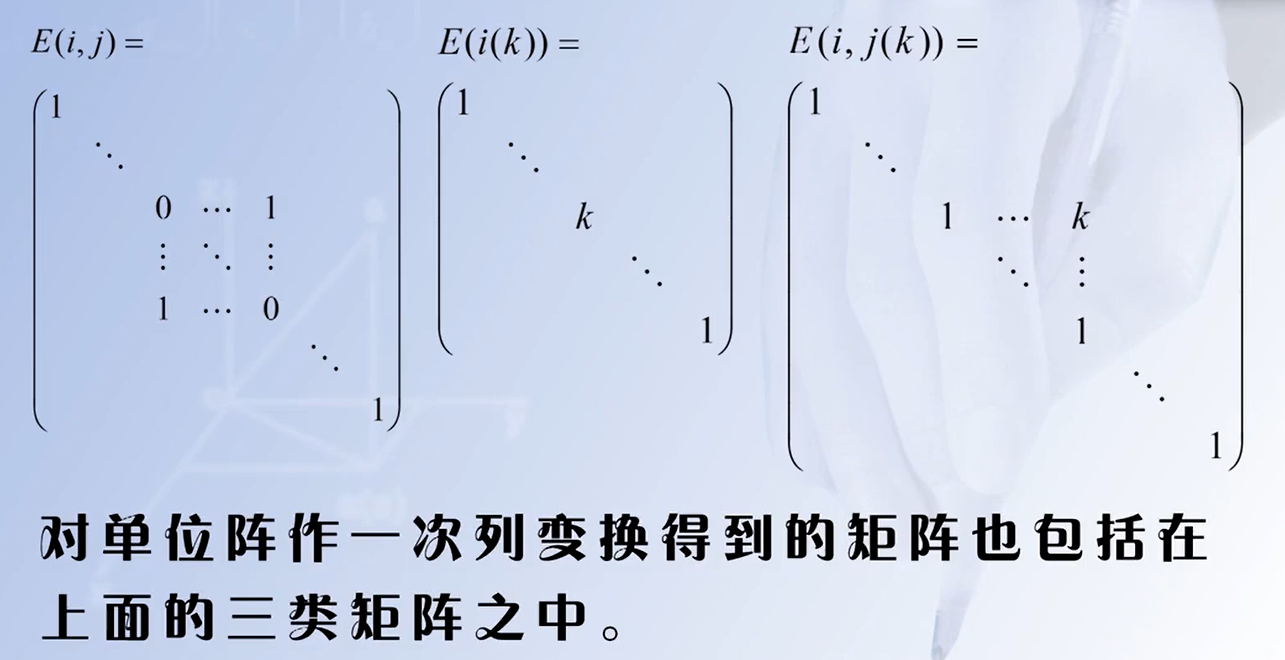
性质:
-
初等矩阵的转置仍为同类型的初等矩阵
-
初等矩阵是非奇异的
∣ E ( i , j ) ∣ = − 1 , ∣ E ( i ( k ) ) ∣ = k , ∣ E ( i , j ( k ) ) ∣ = 1 |E(i,j)|=-1,|E(i(k))|=k,|E(i,j(k))|=1 ∣E(i,j)∣=−1,∣E(i(k))∣=k,∣E(i,j(k))∣=1
2.5.2 初等矩阵与初等变换的关系
行变换相当于左乘初等矩阵;
列变换相当于右乘初等矩阵
问题:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0BHSYBwq-1660358044154)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220724230805037.png)]](https://img-blog.csdnimg.cn/5fdbce20961348af8038c1dfd3adc5e2.png)
定义:若方阵A的秩与其阶数相等,那么A是满秩矩阵,否则A是降秩矩阵
定理:A是满秩矩阵,则A的标准型为同阶单位阵E,即:
A
≅
E
A\cong E
A≅E
推论1:以下命题等价:
- A满秩
- A等价于单位阵
- A非奇异
- A = P 1 P 2 . . . P m ; A = P_1P_2...P_m; A=P1P2...Pm;其中 P i P_i Pi为初等矩阵
证明如下:

推论2:矩阵A与矩阵B等价的充要条件为存在m阶及n阶满秩矩阵P、Q,使 B m × n = P m A m × n Q n B_{m\times n} = P_mA_{m\times n}Q_n Bm×n=PmAm×nQn
由此还可以得到:若P、Q为满秩阵,则
r
(
A
)
=
r
(
P
A
)
=
r
(
P
A
Q
)
=
r
(
A
Q
)
r(A) = r(PA) = r(PAQ) = r(AQ)
r(A)=r(PA)=r(PAQ)=r(AQ)

2.6 矩阵的逆
2.6.1 矩阵逆的概念
定义:对n阶方阵A,若有n阶矩阵B使 A B = B A = E AB=BA=E AB=BA=E,则称B是A的逆矩阵,称A是可逆的。
-
逆矩阵是唯一的,A的逆记做 A − 1 A^{-1} A−1
证明:设B,C都是A的逆,则有: B = E B = ( C A ) B = C ( A B ) = C E = C B=EB=(CA)B=C(AB)=CE=C B=EB=(CA)B=C(AB)=CE=C,即逆阵唯一
-
并非每个方阵都可逆
2.6.2 逆阵存在的条件
由伴随矩阵的知识:
A
A
∗
=
A
∗
A
=
∣
A
∣
E
AA^*=A^*A=|A|E
AA∗=A∗A=∣A∣E
那么有上式知:当
∣
A
∣
≠
0
|A|\neq 0
∣A∣=0时,方阵是可逆的。
定理:n阶方阵A可逆的充要条件是 ∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0
2.6.3 逆矩阵的求法
2.6.3.1 伴随矩阵求法
A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{|A|}A^* A−1=∣A∣1A∗
定理:n阶方阵A可逆的充要条件是
∣
A
∣
≠
0
|A|\neq 0
∣A∣=0充要性的证明:
"
⇒
"
:由
A
可逆知
A
A
−
1
=
E
,两边取行列式,
∣
A
A
−
1
∣
=
∣
A
∣
∣
A
−
1
∣
=
∣
E
∣
=
1
⇒
∣
A
∣
≠
0
"
⇐
"
:由
∣
A
∣
≠
0
,
A
A
∗
=
A
∗
A
=
∣
A
∣
E
⇒
A
(
1
∣
A
∣
A
∗
)
=
(
1
∣
A
∣
A
∗
)
A
=
E
⇒
A
−
1
=
1
∣
A
∣
A
∗
"\Rightarrow":由A可逆知AA^{-1}=E,两边取行列式,\\ |AA^{-1}|=|A||A^{-1}|=|E|=1\Rightarrow |A|\neq 0\\ "\Leftarrow":由|A|\neq 0,AA^*=A^*A=|A|E\Rightarrow A(\frac{1}{|A|}A^*)=(\frac{1}{|A|}A^*)A=E\\ \Rightarrow A^{-1}=\frac{1}{|A|}A^*
"⇒":由A可逆知AA−1=E,两边取行列式,∣AA−1∣=∣A∣∣A−1∣=∣E∣=1⇒∣A∣=0"⇐":由∣A∣=0,AA∗=A∗A=∣A∣E⇒A(∣A∣1A∗)=(∣A∣1A∗)A=E⇒A−1=∣A∣1A∗
2.6.3.2 初等变换法
A 可逆 ⇒ A − 1 可逆 ⇒ A − 1 = P 1 P 2 . . . P s ⇒ P 1 P 2 . . . P s A = E ⇒ P 1 P 2 . . . P s E = A − 1 A可逆\Rightarrow A^{-1}可逆 \Rightarrow A^{-1}=P_1P_2...P_s\\ \Rightarrow P_1P_2...P_s A= E\\ \Rightarrow P_1P_2...P_sE = A^{-1} A可逆⇒A−1可逆⇒A−1=P1P2...Ps⇒P1P2...PsA=E⇒P1P2...PsE=A−1
综上可知:对A和E进行完全相同的初等变换,待
A
A
A变为
E
E
E时,
E
E
E变为
A
−
1
A^{-1}
A−1
(
A
:
E
)
→
.
.
.
→
(
E
:
A
−
1
)
(A:E)\rightarrow ... \rightarrow (E:A^{-1})
(A:E)→...→(E:A−1)

2.6.3.3 定义求法
定义:对n阶方阵,若有n阶矩阵B,使得 A B = B A = E AB=BA=E AB=BA=E,则称B是A的逆矩阵,称A是可逆的。
性质: A B = E ( o r B A = E ) ⇒ B = A − 1 AB=E(or\ BA=E)\Rightarrow B=A^{-1} AB=E(or BA=E)⇒B=A−1
故:对于n阶方阵,只需要找到一个n阶矩阵B,使得 A B = E AB=E AB=E或者 B A = E BA=E BA=E即可。


2.6.3.4 证明逆矩阵
2.6.4 逆矩阵的性质
{ A 可逆 ⇒ ∣ A − 1 ∣ = 1 ∣ A ∣ A 可逆 ⇒ A − 1 可逆, ( A − 1 ) − 1 = A A B = E ( o r B A = E ) ⇒ B = A − 1 ( A T ) − 1 = ( A − 1 ) T ( A B ) − 1 = B − 1 A − 1 ( k A ) − 1 = 1 k A − 1 , ( k ≠ 0 , A 可逆 ) \begin{cases}A可逆\Rightarrow |A^{-1}| = \frac{1}{|A|}\\ A可逆\Rightarrow A^{-1}可逆,(A^{-1})^{-1}=A\\ AB=E(or\ BA=E)\Rightarrow B=A^{-1}\\ (A^T)^{-1}=(A^{-1})^T\\ (AB)^{-1} = B^{-1}A^{-1}\\ (kA)^{-1}=\frac{1}{k}A^{-1},(k\neq 0,A可逆) \end{cases} ⎩ ⎨ ⎧A可逆⇒∣A−1∣=∣A∣1A可逆⇒A−1可逆,(A−1)−1=AAB=E(or BA=E)⇒B=A−1(AT)−1=(A−1)T(AB)−1=B−1A−1(kA)−1=k1A−1,(k=0,A可逆)
注意一个没有的性质: ( A + B ) − 1 ≠ A − 1 + B − 1 (A+B)^{-1}\neq A^{-1}+B^{-1} (A+B)−1=A−1+B−1
证明:初等矩阵都可逆

综上,初等矩阵的三个性质:
1.初等矩阵的转置
2.初等矩阵都是非奇异的矩阵
3.初等矩阵的逆阵仍为同类型的初等矩阵
2.7 分块矩阵
2.7.1 概念与定义
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tYJh1vft-1660358044156)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220725160631522.png)]](https://img-blog.csdnimg.cn/b8ddacdd9c6149918c865aa430bbaf43.png)
2.7.2 分块矩阵的运算
-
线性运算 加法与数乘
-
乘法运算 符合乘法的要求
-
转置运算 大块小块一起转
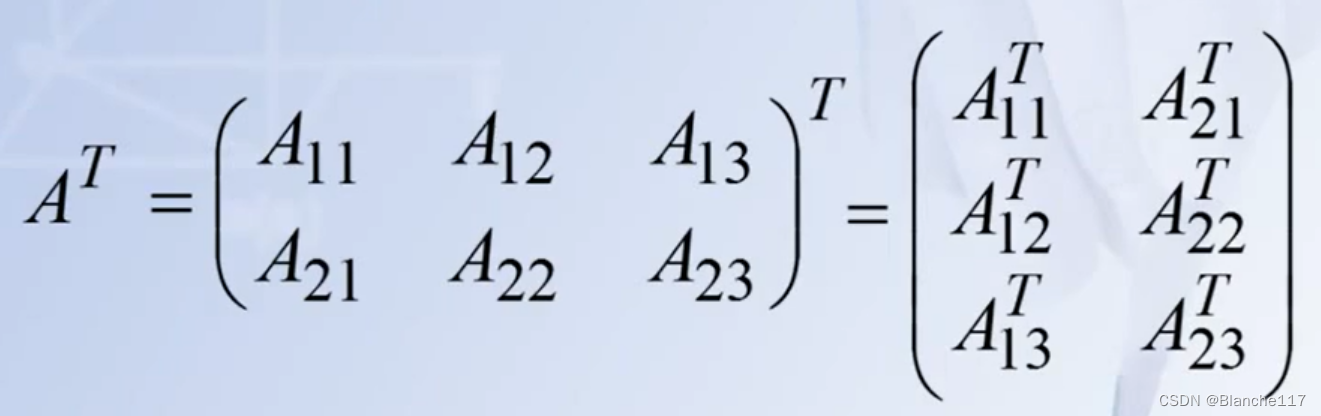
2.7.3 几种特殊的分块矩阵
2.7.3.1 分块矩阵
- 准对角阵

∣ A ∣ = ∣ A 1 ∣ A 2 ∣ . . . ∣ A s ∣ |A| = |A_1|A_2|...|A_s| ∣A∣=∣A1∣A2∣...∣As∣
A可逆的充要条件是每一个小块都可逆

r ( A ) = r ( A 1 ) + r ( A 2 ) + . . . + r ( A s ) r(A) =r(A_1)+r(A_2)+...+r(A_s) r(A)=r(A1)+r(A2)+...+r(As)

- 分块三角阵

-
分块斜对角阵
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KgeyAnmF-1660358044158)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220725162338356.png)]](https://img-blog.csdnimg.cn/5644bb0c0c784c2a99b3421da57d0892.png)
2.8 矩阵方程——逆矩阵的应用
矩阵方程的三中类型:
-
AX=B
-
XA=B

- AXC=B
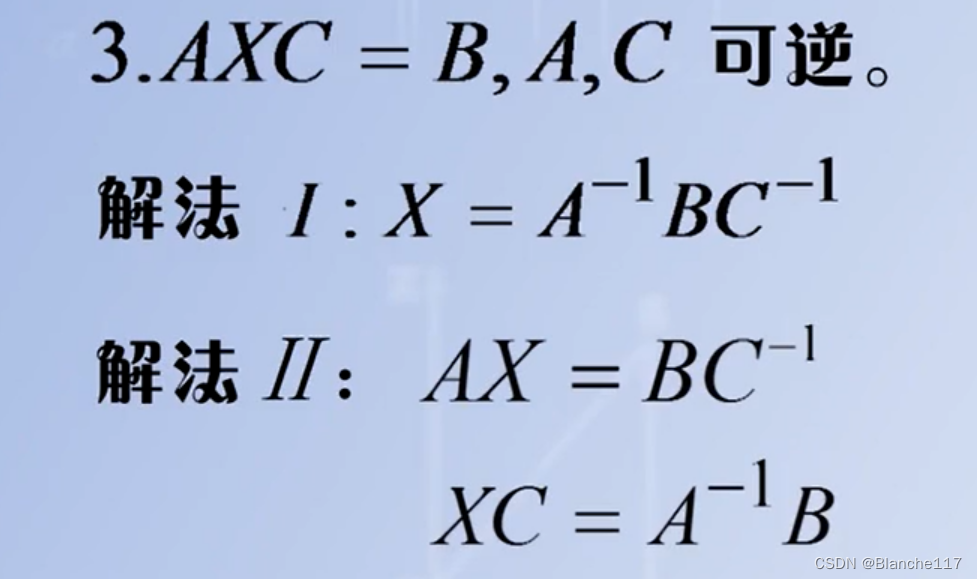
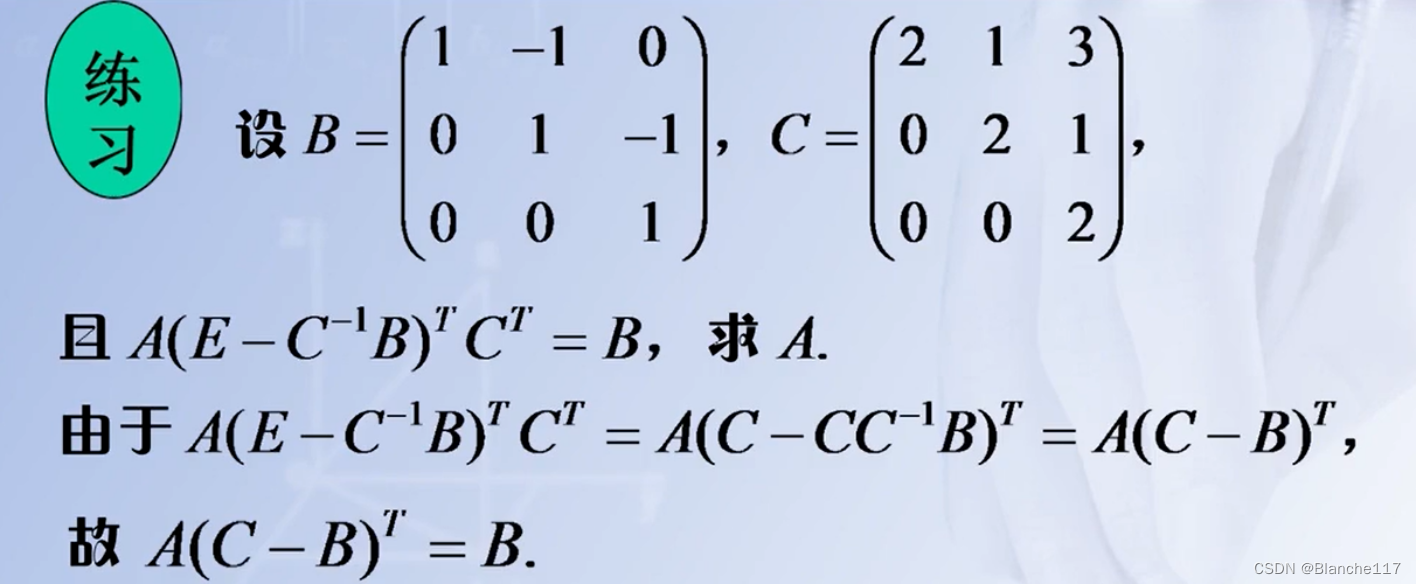
一定要先化简,再求解






















 2639
2639











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










