第三章 简单的优化模型

第三章 简单的优化模型

本章介绍简单的优化模型，归结为微积分中的函数极值问题，直接用微分法求解。

建立优化模型的步骤：

• 做出若干合理简化的假设

• 首先确定优化的目标、寻求决策和决策受到的限制

• 运用数学工具（变量、常数、函数）解决

• 最后运用微分法求出最优决策

以下选出几个实例学习

---

1.存贮模型

1.1不允许缺货的存贮模型

问题：
配件厂生产若干种部件，每次生产因更换设备要付生产准备费（与生产数量无关），部件生产大于需求时占用仓库要付贮存费。设计生产计划，确定生产周期，单个周期产量，可使日均费用最少。

问题分析：
经过试算可以发现，生产周期短、产量小，会使贮存费小，准备费大；而周期长、产量大，会使贮存费大，准备费小。连续性变化，必然存在一个中间值为最佳周期，达到日均费用最小。

模型假设：

• 使用连续模型，生产周期T和产量Q视为连续性变量。
• 每天需求量为常数r，生产准备费为C₁,每天每件产品贮存费为C₂。
• 生产能力足够大，不允许缺货。

模型建立：
$$Q=rT$$

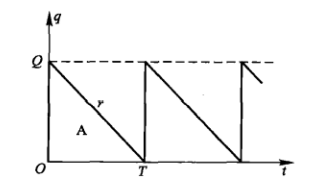
一个周期内的贮存费
$$C=C_1+C_2{\int }_0^{T}q(t)dt=C_1+C_{2}r{T}^2/2$$
日均费用
$$\overline{C}=C_1/T+C_{2}rT/2$$
取最小值得
$$\begin{gathered} T=\sqrt{\frac{2C_1}{C_{2}r}} \\ Q=\sqrt{\frac{2C_{1}r}{C_2}} \\ {C}_{min}=\sqrt{2C_1{C}_{2}r} \end{gathered}$$

1.2允许缺货的存贮模型

模型假设：
与上述模型类似，只是生产能力足够大，允许缺货，每天每件产品损失费为C₃,缺货数量在下次生产补足。

模型建立：
$$Q=r{T}_1$$

可得总费用为
$$C=C_1+C_2{\int }_0^{T_1}q(t)dt-C_3{\int }_{T_1}^{T}q(t)dt=C_1+C_{2}r{T_1}^2/2+C_{3}r(T-T_1{)}^2/2$$
日均费用，化为关于T、Q的二元函数
$$\overline{C}(T,Q)=\frac{C_1}{T}+\frac{C_2{Q}^2}{2rT}+\frac{C_3(rT-Q{)}^2}{2rT}$$
T、Q的偏导均为零得到T、Q的最优解

---

2.求解杯子的重心模型

问题：
杯子的重心随着杯中液体的液面高度的变化而变化，在液面升高过程中，重心会先降低后又升高，其中必然存在一个最低点，建立模型求解最低点，最不容易倾倒的状态。

问题分析：
杯子的重心由杯中液体、杯侧壁和底盘质量共同决定；并且重心在杯子的中轴线上下移动。结合物理背景知识，物体重心计算公式（等效力矩 <印象中>）。为简化问题，不妨从忽略底盘质量开始考虑。

模型一假设：

• 杯子材料均匀分布，形状为圆柱体，高为单位1
• 满杯状态的液体质量为W₁，则液面高度为x时，质量为xW₁，液体重心S₁=x/2
• 侧壁质量为W₂，底盘质量忽略不计，杯子重心S₂=1/2

模型一建立：

物理重心求解
$$(x{W}_1+W_2)S=S_{1}x{W}_1+S_2{W}_2$$
可以求解得到
$$S(x)=\frac{x^2+a}{2(x+a)}$$
令
$$\begin{gathered} \frac{dS}{dx}=0 \\ {x}^{\ast }=\sqrt{a^2+a}-a \\ (质量比a=\frac{W_2}{W_1}) \end{gathered}$$
进一步验证知液面高度与杯子重心重合时，重心最低。

模型二建立：

考虑杯底盘质量W₃，易知重心S₃=0
$$(x{W}_1+W_2+W_3)S=S_{1}x{W}_1+S_2{W}_2+S_3{W}_3$$

$$\begin{gathered} S(x)=\frac{x^2+a}{2(x+a+b)}(a=\frac{W_2}{W_1},b=\frac{W_3}{W_1}) \\ {x}^{\ast }=\sqrt{(a+b{)}^2+a}-(a+b) \end{gathered}$$

得到相同形式的结果：液面与杯子重心重合时的重心最低。有实际数据可证模型一产生的误差可控，简化方式同时合理。

模型推广：
这个所建立的模型同样适用其他形状的杯子，只不过求解过程会变复杂，方法不变。只要杯子为旋转体，重心最低处的条件仍旧成立。

---

3.经济学 商品效用

效用函数

人们商品消费、服务消费所获得的生理、心理上的满足程度称为效用。

效用函数U(x)表示数量为x的某种商品产生的效用

其导函数表示商品数量增加一个单位时U(x)的增量，称为边际效用

遵循原则：边际效用递减
$$\frac{dU}{dx}>0,\frac{d^{2}U}{d{x}^2}<0$$
一种商品的典型效用函数表达式
$$U(x)=a{x}^{\alpha },a>0,0<\alpha <1$$
两种商品的典型效用函数表达式
$$U(x,y)=a{x}^{\alpha }{y}^{\beta },a>0,0<\alpha <1,0<\beta <1$$
对于U(x,y)可引入无差别曲线，效用相同的点的集合
$$\begin{gathered} U(x,y(x))=a{x}^{\alpha }{y}^{\beta },a>0,0<\alpha <1,0<\beta <1 \\ U(x,y)=u \end{gathered}$$

效用最大化模型

假设甲乙两种商品单价分别为p₁，p₂；消费者花费s；购买数量为x，y。

效用最大模型满足以下条件
$$\begin{gathered} maxU(x,y) \\ s.t.p_{1}x+p_{2}y=s \end{gathered}$$
模型几何解法

消费点Q在消费曲线上运动，要使效用最大，必然是切点

数学解法

拉格朗日数乘法求解

可以得到效用最大化原理：当两种商品的边际效用与二者价格之比相同时，效用最大
$$\frac{\delta U/\delta x}{\delta U/\delta y}=\frac{p_1}{p_2}$$
推广：n种商品

---

更多实例冰山运输、影院视角(概率论中变异系数)、易拉罐优化设计(2006年C题)