【DSP】运用FFT抑制一维数据中的高频分量（Python及Java安卓实现）

如果已经对傅里叶变换有深刻的理解，想直接看代码，建议直接往后点。前半部分感觉还不够完整，后面有机会再修改。

FFT与DFT

FFT(Fast Fourier Transformation)，快速傅里叶变换，是一种快速实现离散傅里叶变换DFT的方法。该算法也是数字信号处理里非常重要的一个算法。由于时间关系，在这篇文章中，主要还是讲运用，就先不赘述FFT的详细原理了。关于FFT的原理，如果有机会再另开篇整理~
不过还是要随便记录一下自己的理解。

个人对傅里叶变换的理解

不得不说，傅里叶实在是太厉害了！作为一个通信人，好多门课都会和傅里叶打交道。时域和频域之间的转换，确实非常美妙呢。我在这儿短短一篇也讲不清，推荐一篇通俗易懂的深入浅出的讲解傅里叶变换。
傅里叶变换的根基就是，所有信号都可以用某频率某振幅某相位的正弦波的叠加来表示！
$$x=\sum _{i=-\infty }^{+\infty }{a}_{i}sin({\omega }_i+{\varphi }_i)$$
这么一来，时域上的信号，便能转换为频域上的信号，每个频域点代表一定的频率，而相应的幅值和相位则是相应正弦波的振幅和相位。

傅里叶变换会出现复数，然后就会出现实部和虚部，这个又怎么理解呢？
一个复数，可以用实部和虚部表示，也可以用模和相位表示。而模和相位则对应着信号的幅值和相位。
好像更多的时候，我们更加关心它的幅值，而不是相位，这个在各大语言中基本都能用一个abs来实现。

关于采样以及DFT的很抽象的理解

记得信号与系统老师和我们说过，时域和频域上，周期对应离散，非周期对应连续。那么DFT就是个周期离散对应周期离散的例子…
当我们拥有一个时域的连续周期信号，周期上就是一个离散的非周期信号～其实也可以理解为，时域上采样频率无穷大，所以频域上一个周期也无穷大。不过呢，我们获取信号，时域上总归是要以一定的频率采样的，于是，在频域上，就开始周期化～而这个周期的大小呢，会与采样频率有关。
我们在时域进行采样，那么频域上在一个周期内的最高频率，也就是这个采样频率。
_{我们把信号从时域转换到频域，所能得到得最大的频率肯定只能是采样时所用的频率嘛。就算时域有更加高频的信号，也只会产生混叠，混入该范围的频率中去了。}

那么采样点数，又会带来什么影响呢？
我们以一定的频率，对信号进行采样，信号越长，我们采样的点数会越多，但是我们采样的频率保持不变，所以频域上的最高频率便保持不变，改变的只能是频率点之间的间隔，或许也能理解为频域的分辨率。也就是说，我们采样的点数，在这个最高频率间均匀分布！采样点数越多，我们能获得的分辨率也就越高~

FFT的应用之抑制高频分量

整体的思路就是，将信号从时域转换到频域，然后用低通滤波器进行滤波，最后再从频域转换回时域上去。我们的时域信号是离散信号，此处可以用DFT来处理。
那我们要如何获得这个低通滤波的截止频率呢？这就得看具体的运用需求啦。

Python实现

先简单说明一下——这里是在实现一个类似于列检测的功能，每个图像列与列之间的间距基本一致，不过会有些高频噪音，所以这里用傅里叶变换来抑制。不过这个列检测，是把图像从二维变为一维才处理的，所以这里只是一维数据。

在Python中调用numpy，实现起来非常容易~直接调用np.fft中的函数就可以实现DFT了，整体上和matlab中差不多。
而理想低通滤波直接用了个掩膜来实现，使得频率在较高时为零，即抑制了高频分量。
为了更加直观且方便LPF的实现，这里做了个fftshift，让其做了个平移，使得信号定义域从原来的 $[0,N)$ 到了 $[-N/2,N/2)$ ，因为频域是个周期的对称的离散信号，所以怎么平移都是没问题的。
来直观地感受下这个平移（左边是平移前，后边是平移后。）

在平移后，处于center的就是直流分量~（其实这些都是离散的，不过画成连续的好看点）。这样的话，要进行低通滤波就直接在center左右截至就好。
接下来就是关键的代码啦！

# -*- coding: utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt

#din为输入的信号
#D为设置的截至频率点
def rmHF(din, D):
    #draw the original signal (time domain)
    N=len(din)
    plt.subplot(221)
    plt.plot(din)
    plt.title("the input signal (time domain)")
    
    #perform fft on the signal
    fft_d=np.fft.fft(din) 
    f_shift = np.fft.fftshift(fft_d)
   # f_shift =f_shift/N  #normalized
    
    # draw the original signal (frequency domain)
    plt.subplot(222)
    x=np.arange(N)
    abs_p=np.abs(f_shift)      #the amplitude of the signal
    plt.plot(x,abs_p,'g') #连续画法
    #plt.stem(x,abs_p,'g',use_line_collection=True) #离散画法
    plt.title('FFT-performed input signal (frequency domain)') 

    # ideal low pass filter
    centre=int(N/2)
    mask=np.zeros(len(fft_d), dtype='uint8')
    mask[centre - D:centre + D + 1] = 1
    f_shift = f_shift * mask

    plt.subplot(223)
    abs_f=np.abs(f_shift)
    plt.plot(x,abs_f,'g')    
    plt.title('signal after LPF (frequency domain)') 
    
    # ifft performed
    f_ishift = np.fft.ifftshift(f_shift)
    dout = np.fft.ifft(f_ishift)
    dout_abs = np.abs(dout)
   
    plt.subplot(224)
    plt.plot(dout_abs)
    plt.title('signal after LPF (time domain)') 
    

一个效果图——

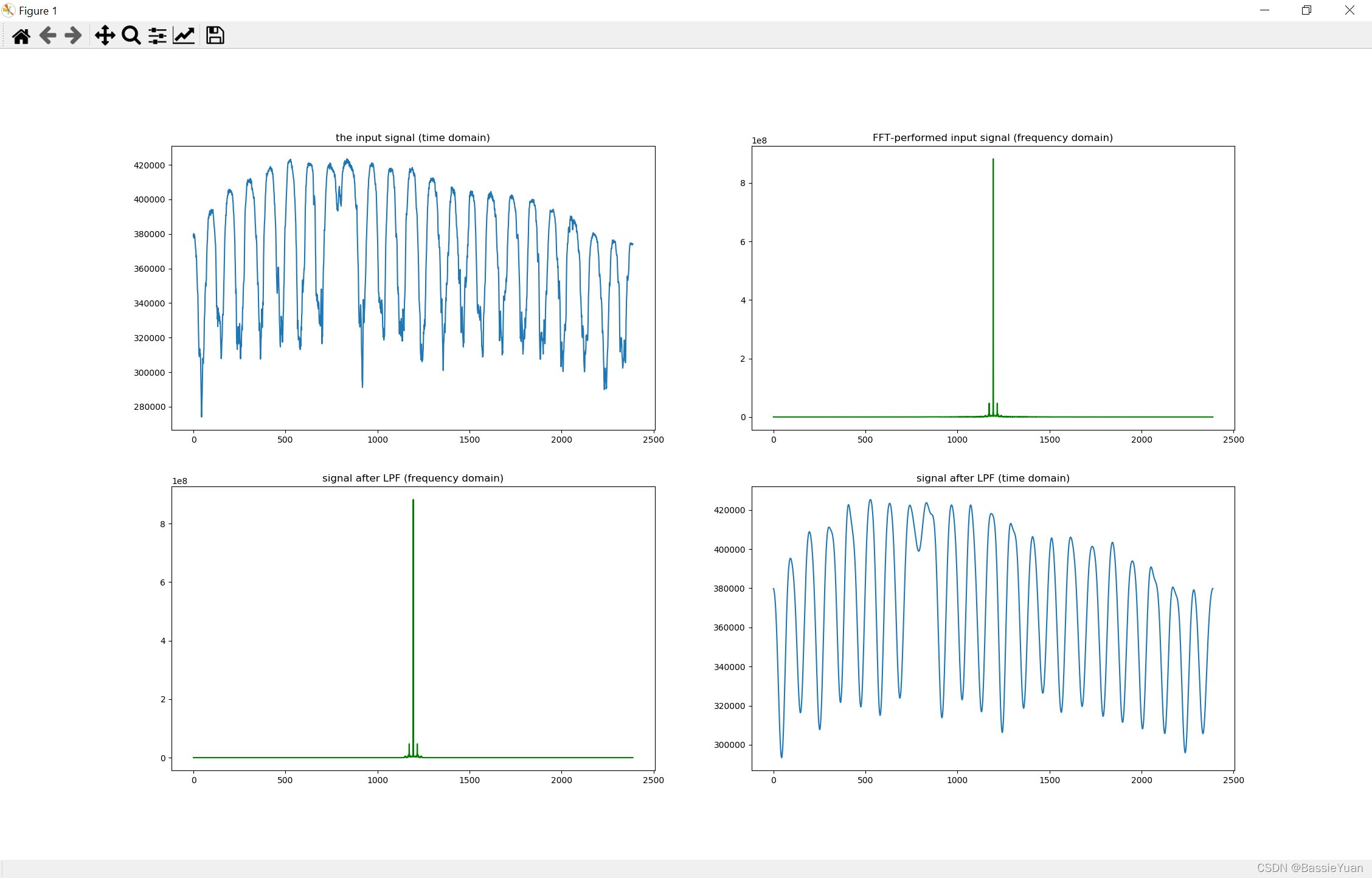
因为上面用的是plot函数，所以画出来的是连续信号，不过实际上DFT输入输出都是离散信号，但是那样画出来有点丑，所以还是用plot吧。不过呢，在频域上用离散信号还是比较合理的，用stem函数，看看效果——

最中间那条就是直流分量啦。也就是频率为零的部分。而两侧次高的其实也就是我这次想要得到的主要的频率。所以就根据那两点定一个理想低通滤波器，修改后的代码如下。最后的结果在上一张图上有所体现~

# ideal low pass filter
    center=np.argmax(abs_p)
    abs_pe=abs_p.view() #复制
    abs_pe[np.argmax(abs_p)]=0 #使得直流分量为0，方便找次高点
    D=abs(np.argmax(abs_pe)-center) #the stop frequency
    D=D+10 #这个10是由于项目其他需求取的
    mask=np.zeros(len(fft_d), dtype='uint8')
    mask[centre - D:centre + D + 1] = 1 #掩膜
    f_shift = f_shift * mask

Android（Java）实现

此处参考了Java jtransforms做简单fft变换这篇文章。
相关文档在此奉上——JTransforms。

由于项目需求，需要调用手机的加速度传感器，然后对其中的数据进行FFT的处理，所以得在安卓上运行。

JTrasform讲解

首先呢，在build.gradle文件里头加上依赖：

dependencies {
    //还有些其他与该功能无关的依赖，此处省略
    implementation 'com.github.rwl:jtransforms:2.4.0'
}

在需要调用FFT函数的文件头加上

import edu.emory.mathcs.jtransforms.fft.*;

在该文件上就可以运用这个包里的函数啦。
这里列举其中几个函数，由于从手机传感器中获取的数据为float类型，此处就以Class FloatFFT_1D中的函数为例~在其他类中也都大同小异。
为了方便理解，先假设我们所输入的是一个长度为n的信号。

函数	输入数组长度	描述
void complexForward(float[] a)	2n	DFT变换。输入为复数。输入数组a中实部虚部交替放置；得到的数组a为相应的完整的FFT变换结果。
void complexInverse(float[] a, boolean scale)	2n	DFT反变换。与complexForward相反。当scale为false，其结果会是原来输入的n倍；当scale为true，与FFT前的数据基本一致。
void realForward(float[] a)	n	DFT变换。由于输入的是实信号，输入数组a中放置信号均为实信号；得到的数组a中实部虚部交替，为相应的FFT变换结果中的前半部分，由实信号FFT的对称性可以得到完整的FFT。
void realInverse(float[] a, boolean scale)	n	DFT反变换。与realForward相反。
void realForwardFull(float[] a)	2n	DFT变换。由于输入的是时域实信号，输入数组a中前n位放置信号，即只放实部；得到的数组a中实部虚部交替，与complexForward得到的结果相同(如果输入为实信号)。
void realInverseFull(float[] a, boolean scale)	2n	DFT反变换。由于输入的是频域实信号，输入数组a中前n位放置信号，即只放实部；得到的数组a中实部虚部交替，与complexInverse得到的结果相同(如果输入为实信号)。

接下来，可以开始运用这些函数啦。

实现之前的小插曲（关于realForward）

由于我们这次处理的都是实信号，方便起见，此处先试一试realForward和realInverse两个函数。
但是在尝试过程中，发现了点（我没看清楚文档而导致的）小问题——

   public void FFTtry(){
        FloatFFT_1D fft = new FloatFFT_1D(10);
        float[] a = new float[10];
        int num = 1;
        for(int i = 0; i < 10; i += 1){
            a[i] = num;
            num++;
        }
        System.out.println();
        System.out.println("Before fftw"+ Arrays.toString(a));

        fft.realForward(a);
        System.out.println("After fftw"+ Arrays.toString(a));
        
        fft.realInverse(a,true);
        System.out.println("After ifftw"+ Arrays.toString(a));
    }

Before fftw[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
After fftw[55.0, -5.0, -4.9999995, 15.388418, -5.0, 6.8819094, -5.0, 3.6327124, -5.0000005, 1.624598]
After ifftw[1.0, 2.0, 2.9999998, 4.0, 5.0, 6.0, 7.000001, 8.0, 9.0, 10.0]

这是用realForward传入传出的例子。
由于对java里的fft不熟悉，我同步在Python中求FFT，来进行一个对比。
试试

[55.+0.00000000e+00j -5.+1.53884177e+01j -5.+6.88190960e+00j -5.+3.63271264e+00j -5.+1.62459848e+00j -5.-1.33226763e-15j -5.-1.62459848e+00j -5.-3.63271264e+00j -5.-6.88190960e+00j -5.-1.53884177e+01j]

为了方便对比，此处输出也只取一半的值，我这里就让精度稍微低些，方便对比。

[55.+0.00000000e+00j -5.+1.53884177e+01j -5.+6.88190960e+00j] -5.+3.63271264e+00j -5.+1.62459848e+00j 

经过对比发现，这个算出来的好像并不是直接直接取前半部分，不然的话第一个值的复数部分应该为零，而这里得到了-5。好了，突然才发觉自己理解错了（捂脸）。这个-5是第六位的实部Re[5]！ 而第六位的虚部非常接近0，其实由对称性可知，理论上应该就是0，这里是误差所致，忽略不计~
_{这里简单解释以下为什么理论上是零。因为对于偶长度实信号来说，其DFT是共轭对称的。也就是实部为偶函数，虚部为奇函数。这个可以直接观察以下上面的结果，很容易发现。那么作为对称中心，它的虚部就应该取零啦！}

所以呢，正确的打开方式是这样——

唉，这就对了嘛！人家说的明明白白，当数据长度为偶数时，在a[1]取的是Re[n/2]，只能怪自己没有好好阅读文档了。
不过问题总算迎刃而解了~我们继续！
如果用的是其他的几个函数，就不会出现这样糟糕的问题了。也就只有realForward和realInverse两个函数是这么设定的。我这里是贪图方便，想直接用获取的实信号数组来处理，懒得生成一个两倍长的数组了。
_{这也太懒了！不过或许有时懒是发明创造的动力源泉呢（bushi}

具体代码实现

讲了这么多，我都快忘了我最开始的目标了…那就是…去除高频分量！
我这里就以上面所提及的函数为例来写代码啦~
先来试一试，看看想法对不对。

   public void FFTtry(){
        FloatFFT_1D fft = new FloatFFT_1D(10);
        float[] a = new float[10];
        int num = 1;
        for(int i = 0; i < 10; i += 1){
            a[i] = num;
            num++;
        }
        System.out.println();
        System.out.println("Before fftw"+ Arrays.toString(a));

        fft.realForward(a);
        System.out.println("After fftw"+ Arrays.toString(a));
        
		//这里截至频率点取的是2
        for(int d=6;d<a.length;d++){
        	a[d]=0; a[1]=0;
        }
        
        fft.realInverse(a,true);
        System.out.println("After ifftw"+ Arrays.toString(a));
    }

得出的IFFT与在python中得出的一致

After ifftw[3.5, 1.2639321, 2.263932, 4.5, 5.5, 5.5, 6.5, 8.736069, 9.736068, 7.5]

好的，那就可以来实现最后的目标了

    //参数表（离散实信号value[], 信号长度n, 采样频率Fsample, 截至频率Fstop）
    public float[] FFT_removeHF(float value[], int n, int Fsample, int Fstop){
        FloatFFT_1D fft= new FloatFFT_1D(n);//先创建一个对象
        fft.realForward(value);//对信号进行FFT操作

        //频率点间隔=2 x 采样频率 / 采样点数
        float Finterval=2*(float)Fsample/n;
        //但是由于频域分辨率的原因，我们很难达到所要求的截止频率，所以只能就近取
        //这里假设实际截止频率能稍微大于理想截止频率
        //这里我们计算出截止频率与中心频率的频率点个数
        int Nstop= (int)Math.ceil((double)(Fstop/Finterval));
        //把截止频率以外的频率全部设置为0
        //由于我们用realInverse，所以数组如下
        //如果数组长度n为偶数：[ Re[0] Re[n/2] Re[1] Im[1] Re[2] Im[2] ... Re[n/2-1] Im[n/2-1] ]
        //如果数组长度n为奇数：[ Re[0] Im[(n-1)/2] Re[1] Im[1] Re[2] Im[2] ... Re[(n-1)/2] ]
        //去除高频分量，即去除value[1]以及value[d]即后面的分量
        for(int d=2+2*Nstop; d<n ; d++){
            value[d]=0;
            value[1]=0;
        }

        fft.realInverse(value,true);//因为要恢复出原来的信号，scale设为true
        return value;
    }

那去除高频分量的部分就完成啦~

小结

做项目还是非常有助于理解基础知识的。因为两个项目刚好都碰上了觉得可以用傅里叶变换来实现的地方，感觉自己对傅里叶变换的理解又更深了一些，不过还是一知半解啊，而且看书越看越晕了。写得这么啰嗦也是希望自己再回顾时能够想起当时突然想通透的那些瞬间吧。
造诣有待提高，但是暂时没那么多时间整理了，先搁置了。
后续有机会的话我会把更加完整的项目代码上传上来。有什么理解有误的地方还望大佬指正！