在机器学习决策树中,最常用的三种算法有三种:ID3,C4.5,CART。在这里我将我对ID3算法的理解说一下。
1、定义
ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征,递归地构建决策树。
ID3名字中的ID是It-erative Dichotomiser(迭代二分器)的简称。
2、理解
这种构建树的算法是通过信息增益(不是信息增益率喔!)来进行特征选择的,而信息增益是由两个熵相减得来的,是由经过特征分裂后的熵减去分裂前结点的熵。
熵是什么呢,熵是一种不确定性,一开始你数据的熵肯定是最大的,你建树的目的就是想要把你数据的不确定性一步一步地减少,使一个结点中的数据更纯(也就是我们说的分好了类)。
当前一个熵给定的时候,我们要做的就是使分裂后的熵(entropy(D,A))尽可能地小。
3、ID3算法的过程
ID3算法处理的数据是离散的,它的基本算法过程如下:
创建Root结点
如果Example都为正,
那么返回label=正的单节点数Root
如果Example都为副,
那么返回label=副的单节点数Root
如果Attribute为空,
那么返回Root,label=Example中最普遍的Target_attribute的值。
否则
A←Atrribute中分类Eaxmples能力最好的属性(*)
Root的决策属性←A
对于A的每个可能值Vi
在Root下加一个新的分支对应测试A=Vi
令Examplevi为Examples满足A属性值为Vi的子集
如果Example为空
在新分支下,加一个叶子节点,
结点label=example中最普遍的Target_attribute值。
否则
在新分支下,加一个ID3的子树(包含所有满足的样例,所有标签,但是特征数-1)。
结束
返回Root
从根结点开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该结点的不同取值建立子结点;再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。
3、ID3算法的优缺点
优点
- 1.假设空间包含所有的决策树,搜索空间完整。
- 2.健壮性好,不受噪声影响。
- 3.可以训练缺少属性值的实例。
总的来说,就是理论清晰、方法简单、学习能力较强
缺点
ID3算法的缺点也是很明显,正如我们上面所说,ID3算法会去选择子类别多的特征,因为这样分裂出来的结果会更纯,熵会更小,这有偏于我们的初衷,我们要的纯不是想通过让它分类分的更细得来的纯啊!如果这样那不如分100个类好了里面数据的纯度都很高。
所以我对ID3算法的缺点进行了一些总结:
- 1.ID3只考虑分类型的特征,没有考虑连续特征,比如长度,密度都是连续值,无法在ID3运用。这大大限制了ID3的用途。
- 2.ID3算法对于缺失值没有进行考虑。
- 3.没有考虑过拟合的问题。
- 4.ID3算法在选择根节点和各内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息。
- 5.划分过程会由于子集规模过小而造成统计特征不充分而停止。
4、为什么倾向特征选项较多的特征
在ID3算法中,一般而言,我们根据信息增益来进行判断。信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。
在信息增益中,还有一个“信息熵”的概念。
假定当前样本集合D中第
k
k
k类样本所占的比例为
p
k
(
k
=
1
,
2
…
,
∣
γ
∣
)
p_k(k=1,2…,|γ|)
pk(k=1,2…,∣γ∣),则D的信息熵定义为:

信息增益的公式为:
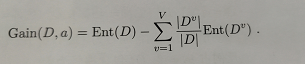
因为考虑到不同的分支结点所包含的样本数不同,给分支结点赋予的权重即样本数越多的分支结点影响就越大。
所以说,ID3算法会倾向于特征选项较多的特征
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








