[学习笔记]策略前展、策略迭代与强化学习1——动态规划

最新推荐文章于 2024-04-10 13:20:06 发布

hozy_Lynnnnn.

最新推荐文章于 2024-04-10 13:20:06 发布

阅读量2k

点赞数 13

分类专栏：【学习笔记】强化学习文章标签：动态规划人工智能学习算法其他

本文链接：https://blog.csdn.net/weixin_45844626/article/details/127304640

版权

【学习笔记】强化学习专栏收录该内容

3 篇文章

订阅专栏

1 exact and approximate dynamic programming principles

1.1 AlphaZero, off-line training, and on-line play

1.2 确定性动态规划

1.2.1 finite horizon problem有限时间问题

1.2.2 动态规划算法

1.2.3 近似值空间

1.3 随机动态规划

1.3.1 finite horizon problem

1.3.2 近似的值空间——stochastic DP

1.3.3 infinite horizon problem

教材：Rollout, Policy Iteration, and Distributed Reinforcement Learning: Dimitri P. Bertsekas

1 exact and approximate dynamic programming principles

1.1 AlphaZero, off-line training, and on-line play

AlphaZero的设计被分为两部分：

（1）off-line training：学习如何评估棋子的位置和使自身棋子的位置处于优势。

AlphaZero在与棋手进行比赛之前，通过自我训练来学习如何下棋，过程中生成chess player和position evaluator序列。其中，

policy network: （chess player）移动到下一位置的概率

value network：（position evaluator）在这个位置胜利的概率

在DP问题中，position被看作是state，position evaluator为cost function（对于给定state的cost-to-go函数），chess player是在给定状态下选择控制的随机策略。

总体的训练算法就是策略迭代的过程，从给定的一个player开始，不断地生成提高的player，最后生成一个最厉害的player。DP的过程是对于给定的状态，根据cost function进行策略评估生成cost后进行策略改进，在所有可选控制中，选择一个使得cost最小的控制作为该状态的策略，再进行。policy iteration可以被分为两个阶段：

（i）policy evaluation策略评估：对于给定的player和state，收集它们下一步的数据点，这些所有的数据点被收集起来训练value network。通过value network来评估position，即计算value function的过程。

（ii）policy improvemen策略t改进：给定player和position evaluator，尝试不同的移动路径并进行评估，调整移动的概率使得player朝着最佳的结果移动，可以看作是训练一个policy network。在AlphaZero中使用了蒙特卡洛搜索树的算法来实现。

（2）on-line play：利用离线的数据，实时的生成移动。

通过离线训练好的数据进行比赛时，可以很快的得到从某个位置到下一个某位置的移动概率，但离线的player无法战胜更强的对手。因此，AlphaZero通过on-line的方式进行策略改进。

on-line play应用在AlphaZero的算法是，对于给定的位置，生成一个到给定深度的lookahead tree（multistep lookahead），利用离线的数据进行更多的移动（truncated rollout：与longer lookahead达到同样效果的方法），最终使用position evaluator获得terminal cost。

在AlphaZero中multistep lookahead已经很长了，因此rollout部分不是很重要，可以不添加。但在Tesauro's 1996 backgammon中使用rollout，并且rollout是实现高性能的关键，这是因为backgammon是随即不确定性的，对于longer lookahead每一步都需要快速的扩展lookahead tree。

1.2 确定性动态规划

DP问题的中心对象是一个离散时间动态系统，其在控制的影响下生成一系列的状态。这个系统可以是确定的或随机的（在随机扰动的影响下）。

1.2.1 finite horizon problem有限时间问题

有限时间问题的有限体现在系统在有限的N个stage里。在时间k下，系统的状态和控制分别表示为 $x_k$ 和 $u_k$ 。在确定性系统中，状态 $x_{k+1}$ 只由 $x_k$ 和 $u_k$ 确定。

$x_{k+1} = f_k\left(x_k,u_k \right )$

其中， $u_k$ 也与 $x_k$ 有关。

state space at time k: 时间k时所有可能的 $x_k$ 的集合

control space at time k: 时间k时所有可能的 $u_k$ 的集合

$f_k$ : 函数可以是任意的，依赖于k

$g_k(x_k,u_k)$ ：隐含的cost function，随时间累加。给定初始状态 $x_0$ ，对于控制序列 $\left\{ u_0,...,u_{N-1} \right\}$ ，控制序列的总代价为 $J(x_0;u_0,...,u_{N-1}) = g_N(x_N) + \sum_{k=0}^{N-1}g_k(x_k,u_k)$ ，取决于 $g_k$ ，其中 $g_N(x_N)$ 是过程结束时产生的终端成本。最终我们希望获得一个总代价最小的控制序列。

离散最优控制问题：当问题的状态和控制空间是离散的时，可以用无环图来描述问题。结点表示每一个状态，弧表示（状态，控制）对。每一条弧线隐含着成本 $g_k$ 。为了处理终端成本，添加了一个人工结点t，stage N的每一个状态都连向状态t，弧成本为 $g_N(x_N)$ 。控制序列由从stage 0到stage N的一条路径表示。有限时间问题被化简为在图上找到一条路径使得cost最少。

一般来说组合优化问题可以表述为确定性有限状态有限时间的优化控制问题。

1.2.2 动态规划算法

确定性有限时间的DP算法，最优子（尾）问题，当子问题是最优的时候，那么整个问题也是最优的。

DP过程：

从 $x_N$ 开始，计算 $g_N(x_N)$ 为 $J_N(x_N)$ 。k时刻最小的的 $J_k$ = min（状态k到状态k+1的代价 + 最小的 $J_{k+1}$ ），从尾序列长度为2开始计算，直到计算到初始状态截至。

获取最短路径的每个结点：从开始状态起始，计算 $u_k^* \in arg \min_{u_k \in U_k(x_k^*)} \left [ g_k(x_k^*,u_k)+J_{k+1}^*(f_k(x_k^*,u_k)) \right ]$ ，最终获得控制序列 $\left\{u_0^*,...,u_{N-1}^* \right\}$ 。

1.2.3 近似值空间

只有计算出 $J_k^*(x_k)$ 后，才能构建最优控制序列，但是由于 $x_k$ 和k的数量可能非常大，难以实现计算。所以采取近似 $J_k^*$ 的方式，表示为 $\widetilde{J_k}$ ，并构造一个次优解 $\left\{\widetilde{u}_0,...,\widetilde{u}_{N-1} \right\}$ （control sequence)。

RL的核心思想：近似值空间

> multistep lookahead

在公式（1.9）运用了one-step lookahead，其对于k解决了one-stage DP problem。在AlphaZero中使用了multistep lookahead，其解决一个l-step DP problem，1< l < N-k，终端成本函数由 $\widetilde{J}_{k+l}$ 确定。在近似方案中，multistep的性能一般比one-step的性能好。其在AlphaZero中起到了关键的作用，l stage被精确的处理了，而不是包含在终端成本中，但这也会更耗时。

> rollout
近似值空间的主要问题就是要构建一个合适的近似cost-to-go函数 $\widetilde{J_k}$ 。 $\widetilde{J_k}$ 可以通过离线训练获得，也可以通过rollout在线获得。在rollout中， $\widetilde{J_k}(x_k)$ 的获得是从状态 $x_k$ 开始，通过运行启发式控制方案，获得轨迹，再进行计算。

> multiagent problem

在多智能体问题下，控制序列的每一个元素的维度为k，即k个智能体，这使得计算量指数型增长，因此通过multiagent or agent-by-agent rollout的方式解决，方法将在后续讲解。

> Q-Factors and Q-learning

公式1.4的变形，引入Q-factors。 $\widetilde{Q}_k(x_k,u_k) = g_k(x_k,u_k) + \widetilde{J}_{k+1}(f_k(x_k,u_k))$ 。

1.3 随机动态规划

1.3.1 finite horizon problem

与确定规划相比，多了随机扰动因子 $\omega_k$ 。 $x_{k+1} = f_k(x_k,u_k,\omega _k)$ 。每个stage的成本为 $g_k(x_k,u_k,\omega _k)$ 。策略由控制序列 $\left\{u_0,..,u_{N-1}\right\}$ ，变成策略函数，最终获得的最优策略为 $\pi = \left\{\mu_0, ...,\mu_{N-1} \right\}$ 。其中控制 $u_k = \mu_k(x_k)$ ，并且对于所有 $x_k$ 满足 $\mu_k(x_k)\in U_k(x_k)$ 。

最优化：找到一个由函数序列组成的策略，使得期望代价最小（确定动态规划是控制序列）

> exp 线性二次优化控制（书p29-31详细过程）

策略是线性函数，成本函数是二次函数

获得结论：最优策略不取决于 $\omega_k$ ，当 $\omega_k$ 被其均值替换后，也没有受到影响，这被称为确定性等价。这通常出现在线性系统和二次成本的问题中。确定性等价可以用作问题近似的基础，用一些典型的值来替换随机量，比如随机量的期望值。

> exp 库存问题->理解随机DP过程（书p32-37 计算过程）

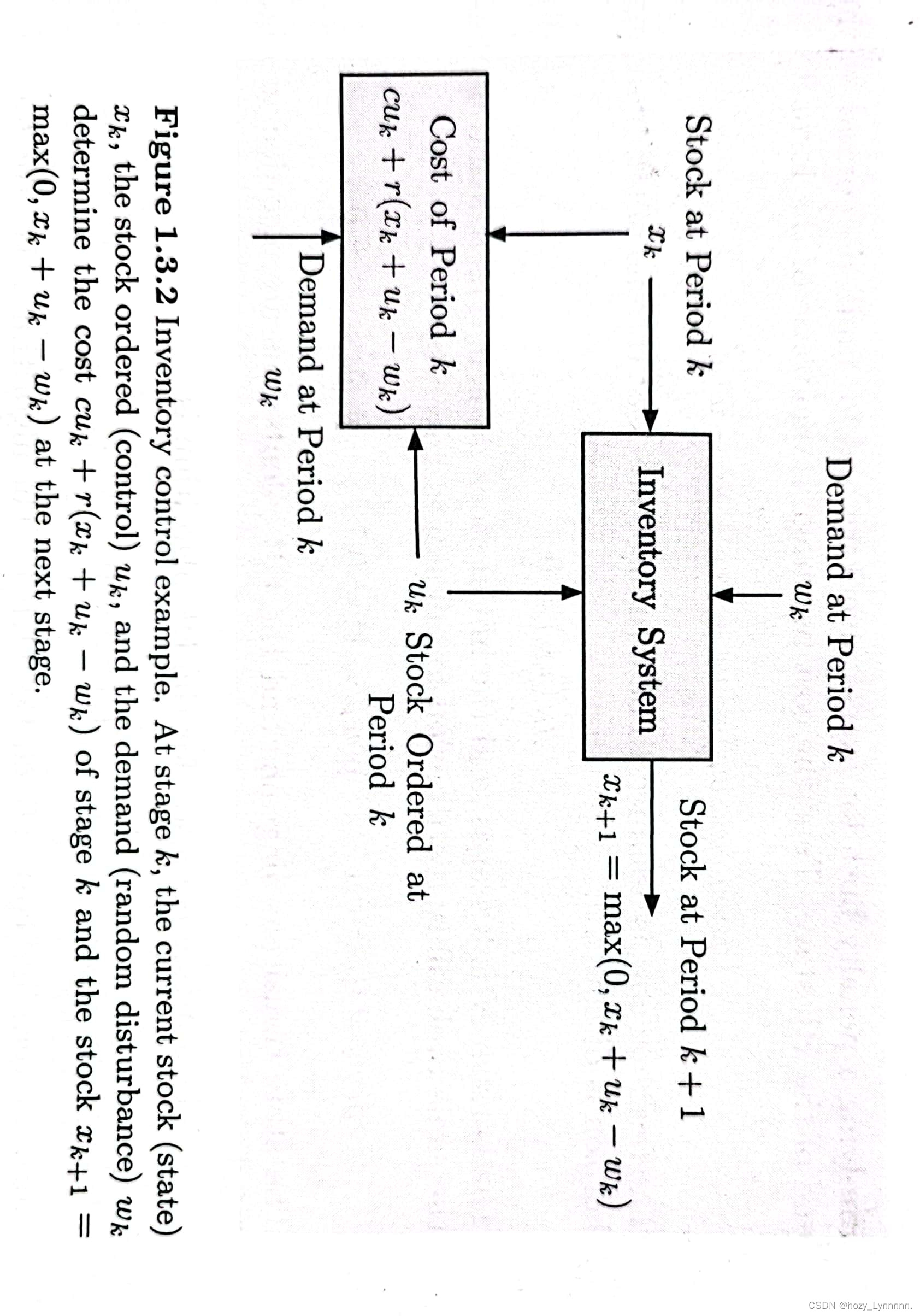
1.3.2 近似的值空间——stochastic DP

三种近似的方式：

1是Simplified Minimization：在多智能体问题上，控制由m个组件组成，可以使用m个单组件最小化序列以减小计算量。
2是Approximate Expected：期望的计算很耗时，在计算期望时采用近似值，如基于蒙特卡洛模拟。
3是 Approximate cost-to-go function $\widetilde{J}_{k+1}(x_{k+1})$ ：近似的方法有问题近似、rollout、参数近似、聚合等。

随机DP也可以引入Q-factor。价值空间的近似可以是cost function近似，也可以利用Q-factor近似。这两种方法的选择主要依据于所要解决问题的内容。

cost function的主要缺点是对于所有控制的期望值需要在线计算，这可能存在着大量的计算。但当系统函数 $f_k$ ，每个stage的成本 $g_k$ 或者控制集合改变时，存在巨大优势，可以使用在线重新规划进行计算，其将提高近似价值空间的鲁棒性。

Q-factor function不支持在线重新规划，但另一方面当问题不需要在线重新规划时，Q-factor不需要去计算期望值，并可以快速地计算出最小化控制 $\widetilde{\mu}_k(x_k)$ 。

1.3.3 infinite horizon problem

无限时间问题即在无限个stage上使得整个问题的成本最小。

$J_{\pi}(x_0) = \lim_{N\to\infty } E_{\omega_k \ _{k=0,1,...}} \left \{ \sum _{k=0}^{N-1} \alpha ^k g(x_k,\mu_k(x_k),\omega_k) \right \}$

其中， $J_{\pi}(x_0)$ 表示给定初始状态 $x_0$ 和策略 $\pi = \left \{ \mu_0,\mu_1,... \right \}$ 的成本， $\alpha$ 是一个折扣因子，一般 $\alpha\leq 1$ 。考虑未来的成本对于离当前状态更远的成本对于当前状态的影响越小，因此使用折扣因子来满足上述情况。

我们将从以下两类问题理解无限时间问题：

（1）随机最短路径问题SSP： $\alpha$ = 1，同时该类问题存在一个特殊的cost-free的终状态，一旦系统到达该状态将会保持在该状态且不产生额外的成本。该终状态被表示为目标状态，尽量使得到达该状态所需的成本最小。我们假设一个问题终将结束，但是需要多少个stage结束是不确定的，即长度是随机的，这由策略来决定。

（2）折扣问题： $\alpha$ < 1，具有有限状态的折扣问题可以转化为SSP。在折扣问题中人工添加一个终状态，系统其他状态移动到终状态的概率为1 - $\alpha$ 。

> 无限时间问题的VI（价值迭代）：

undiscount case:

$J_{k+1}(x) = \min_{u\in U(x)}E_{\omega} \left \{ g(x,u,\omega) +J_k(f(x,u,\omega))\right \},\ k=0,1,...$

discount case:

$J_{k+1}(x) = \min_{u\in U(x)}E_{\omega} \left \{ g(x,u,\omega) +\alpha J_k(f(x,u,\omega))\right \},\ k=0,1,...$

> 近似价值空间

与有限时间相同，使用 $\widetilde{J}$ 来近似价值空间 $J^*$ 。通过one-step lookahead获得 $\widetilde{\mu}$ ， $\widetilde{\mu}(x) \in arg \min_{u_k \in U(x)} E_{\omega} \left \{ g(x,u,\omega) + \widetilde{J}(f(x,u,\omega)) \right \}$

为了便于分析，用 $TJ$ 表示贝尔曼方程的右部，即对于给定的x，

$(TJ)(x) = \min_{u_k \in U(x)} E_{\omega} \left \{ g(x,u,\omega) + \alpha{J}(f(x,u,\omega)) \right \}$

对于每一个 $\mu$ ，引入算子 $T_{\mu}J$ ，对于给定的x，有

$(T_{\mu}J)(x) = E_{\omega} \left \{ g(x,\mu(x),\omega) + \alpha{J}(f(x,\mu(x),\omega)) \right \}$

贝尔曼方程 $J = T_{\mu} J$ 是线性的，因此每一个 $\mu$ 对应一个线性的 $T_{\mu}J$ 。 $TJ$ 可以表示为 $min_{\mu} T_{\mu}J$ 。用 $T$ 和 $T\mu$ 表示VI算法， $J_{k+1 } = TJ_k$ 。当选择了 $\widetilde{\mu}$ 时， $T_{\widetilde{\mu}} \widetilde{J} = T\widetilde{J}$ 。