图像几何变换--缩放、平移、镜像、旋转

已于 2023-03-08 09:26:32 修改
阅读量6.4k 收藏 67
点赞数 3
分类专栏： 数字图像处理 文章标签： 线性代数 深度学习 python opencv c++
于 2021-10-11 20:12:39 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45847073/article/details/120705806
版权
本文详细介绍了图像几何变换的基础概念，包括平移、缩放、旋转和镜像操作的实现过程，以及如何通过变换矩阵进行复合变换。提供了完整代码示例，涵盖了OpenCV库中常用的方法，如最近邻插值和双线性插值。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

一.图像几何变换基础

1.图像的几何变换是指原始图像按照需要产生大小、形状和位置的变化。
2.不改变图像的像素值，而是改变像素所在的几何位置。
3.对于原图像f(x,y)，坐标变换函数
在这里插入图片描述
4.唯一确定了几何变换：
在这里插入图片描述
g(x,y)是目标图像。
5.图像是矩阵，图像的几何变换用矩阵运算来实现。
在这里插入图片描述
6.在数字图像处理中，几何变换由两个基本操作组成：
（1）坐标的空间变换；
坐标变换可由下式表示：
在这里插入图片描述
其中，(v,w)是原图像中像素的坐标，(x,y)是变换后图像中像素的坐标。
最常用的空间坐标变换之一是仿射变换，其一般形式如下：
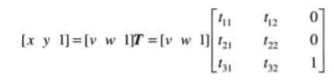
在这里插入图片描述
这个变换可根据矩阵T中元素所选择的值，对一组坐标点做尺度、旋转、平移或偏移。
（2）灰度内插，即对空间变换后的像素赋灰度值。

二.平移

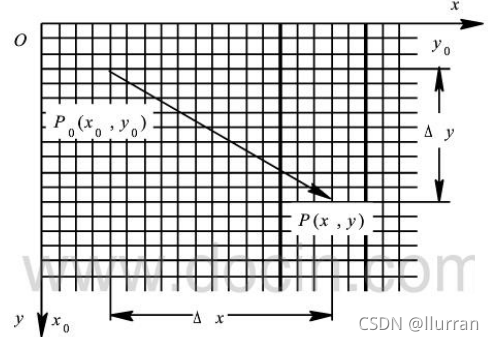
在这里插入图片描述
坐标变换函数：
在这里插入图片描述
用矩阵的形式可表示为：
在这里插入图片描述
（1）齐次坐标
通常将2×3阶矩阵扩充为3×3阶矩阵，以拓宽功能。
点P(x,y)按照3×3的变换矩阵T平移变换的结果。
在这里插入图片描述
可以看出，引入附加坐标后，扩充了矩阵的第3行，并没有使变换结果受到影响。
这种用n+1维向量表示n维向量的方法称为齐次坐标表示法。
（2）平移的变换矩阵
在这里插入图片描述

//平移变换
//tx:水平平移距离，正数向右移动，负数向左移动
//ty:垂直平移距离，正数向下移动，负数向上移动
void trans(Mat& src, Mat& dst, double tx, double ty)
{
	//创建输出图像
	dst.create(src.size(), src.type());
	//平移变换矩阵
	Mat T = (Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, tx, ty, 1);
	//求逆矩阵
	Mat T_inv = T.inv();

	for (int i = 0; i < dst.rows; i++)
	{
		for (int j = 0; j < dst.cols; j++)
		{
			Mat dst_coordinate = (Mat_<double>(1, 3) << j, i, 1);
			Mat src_coordinate = dst_coordinate * T_inv;
			double v = src_coordinate.at<double>(0, 0);  //原图像的横坐标，列，宽
			double w = src_coordinate.at<double>(0, 1);  //原图像的纵坐标，行，高

			if (v >= 0 && w >= 0 && v < src.cols - 1 && w <= src.rows - 1)
			{
				int top = floor(w), bottom = ceil(w), left = floor(v), right = ceil(v);
				double pw = w - top;   //pw为坐标 行 的小数部分
				double pv = v - left;  //pv为坐标 列 的小数部分
				if (src.channels() == 1)
				{
					//灰度图像
					dst.at<uchar>(i, j) = (1 - pw) * (1 - pv) * src.at<uchar>(top, left)
						+ (1 - pw) * pv * src.at<uchar>(top, right)
						+ pw * (1 - pv) * src.at<uchar>(bottom, left)
						+ pw * pv * src.at<uchar>(bottom, right);
				}
				else
				{
					//彩色图像
					dst.at<Vec3b>(i, j)[0] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[0]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[0]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[0]
						+ pw * pv * src.at<Vec3b>(bottom, right)[0];
					dst.at<Vec3b>(i, j)[1] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[1]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[1]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[1]
						+ pw * pv * src.at<Vec3b>(bottom, right)[1];
					dst.at<Vec3b>(i, j)[2] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[2]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[2]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[2]
						+ pw * pv * src.at<Vec3b>(bottom, right)[2];
				}
			}

		}
	}

}

三.缩放

（1）变换矩阵
图像的几何变换改变了像素的空间位置，建立一种原图像像素与变换后图像像素之间的映射关系，通过这种映射关系能够实现下面两种计算：
①向前映射：原图像任意像素计算该像素在变换后图像的坐标位置。
②向后映射：换后图像的任意像素在原图像的坐标位置。
在这里插入图片描述
（2）插值
①最近邻插值
赋予点(x,y)在像素矩阵中离它最近的点的像素值。
最近邻插值的定位误差最大是半个像素。这种误差在物体具有直线边界时就会显现出来，在变换后可能会呈现阶梯状。
在这里插入图片描述
在这里插入图片描述

//最近邻差值缩放
void nearest(Mat& src, Mat& dst, float sx, float sy)  //原图，处理后图，x方向倍数，y方向倍数
{
	//round函数计算之后结果是小数点后全变为0，但其还是float的，需要强制类型转换
	//计算目标图形尺寸
	int dst_cols = (int)round(src.cols * sx);
	int dst_rows = (int)round(src.rows * sy);
	//创建目标图形
	dst.create(dst_rows, dst_cols, src.type());
	//灰度图像处理
	if (src.channels() == 1)
	{
		for (int i = 0; i < dst.rows; i++)
		{
			for (int j = 0; j < dst.cols; j++)
			{
				//插值计算，输出图像的像素点由原图像对应的最近的像素点得到（四舍五入）
				int i_index = (int)round(i / sy);    //y方向缩放，则行数发生改变
				int j_index = (int)round(j / sx);
				//防止越界
				if (i_index > src.rows - 1)
				{
					i_index = src.rows - 1;
				}
				if (j_index > src.cols - 1)
				{
					j_index = src.cols - 1;
				}
				dst.at<uchar>(i, j) = src.at<uchar>(i_index, j_index);
			}
		}
	}
	//彩色图像处理
	else
	{
		for (int i = 0; i < dst.rows; i++)
		{
			for (int j = 0; j < dst.cols; j++)
			{
				//差值计算
				int i_index = (int)round(i / sy);
				int j_index = (int)round(j / sx);
				//防止越界
				if (i_index > src.rows - 1)
				{
					i_index = src.rows - 1;
				}
				if (j_index > src.cols - 1)
				{
					j_index = src.cols - 1;
				}
				//b
				dst.at<Vec3b>(i, j)[0] = src.at<Vec3b>(i_index, j_index)[0];
				//g
				dst.at<Vec3b>(i, j)[1] = src.at<Vec3b>(i_index, j_index)[1];
				//r
				dst.at<Vec3b>(i, j)[2] = src.at<Vec3b>(i_index, j_index)[2];
			}
		}
	}
}

②双线性插值
当求出的分数地址与像素点不一致时，求出周围四个像素点的距离比，根据该比率，由四个邻域的像素灰度值进行线性插值。
在这里插入图片描述
在这里插入图片描述

void linear(Mat& src, Mat& dst, float sx, float sy)
{
	//计算目标图形尺寸
	int dst_cols = (int)round(src.cols * sy);
	int dst_rows = (int)round(src.rows * sx);
	//创建目标图形
	dst.create(dst_rows, dst_cols, src.type());
	for (int i = 0; i < dst.rows; i++)
	{
		//几何中心对齐
		//中心对齐(OpenCV也是如此)：
			//SrcX = (dstX + 0.5) * (srcWidth / dstWidth) - 0.5
			//SrcY = (dstY + 0.5) * (srcHeight / dstHeight) - 0.5
		double index_i = (i + 0.5) / sx - 0.5;
		//防止越界
		if (index_i < 0)
		{
			index_i = 0;
		}
		if (index_i >= (double)src.rows - 1)
		{
			index_i = (double)src.rows - 2;
		}
		//相邻4×4像素的行（坐标）
		int i1 = floor(index_i);
		int i2 = ceil(index_i);
		//u为得到浮点型坐标的小数部分
		double u = index_i - i1;
		for (int j = 0; j < dst.cols; j++)
		{
			//几何中心对齐
			double index_j = (j + 0.5) / sy - 0.5;
			//防止越界
			if (index_j < 0)
			{
				index_j = 0;
			}
			if (index_j >= (double)src.cols - 1)
			{
				index_j = (double)src.cols - 2;
			}
			//相邻4×4像素的列（坐标）
			int j1 = floor(index_j);
			int j2 = ceil(index_j);
			//u为得到浮点型坐标的小数部分
			double v = index_j - j1;
			//处理灰度图像
			if (src.channels() == 1)
			{
				dst.at<uchar>(i, j) = (1 - u) * (1 - v) * src.at<uchar>(i1, j1)
					+ (1 - u) * v * src.at<uchar>(i1, j2)
					+ u * (1 - v) * src.at<uchar>(i2, j1)
					+ u * v * src.at<uchar>(i2, j2);
			}
			//处理彩色图像
			else
			{
				dst.at<Vec3b>(i, j)[0] = (1 - u) * (1 - v) * src.at<Vec3b>(i1, j1)[0] 
					+ (1 - u) * v * src.at<Vec3b>(i1, j2)[0]
					+ u * (1 - v) * src.at<Vec3b>(i2, j1)[0] 
					+ u * v * src.at<Vec3b>(i2, j2)[0];
				dst.at<Vec3b>(i, j)[1] = (1 - u) * (1 - v) * src.at<Vec3b>(i1, j1)[1] 
					+ (1 - u) * v * src.at<Vec3b>(i1, j2)[1] 
					+ u * (1 - v) * src.at<Vec3b>(i2, j1)[1] 
					+ u * v * src.at<Vec3b>(i2, j2)[1];
				dst.at<Vec3b>(i, j)[2] = (1 - u) * (1 - v) * src.at<Vec3b>(i1, j1)[2]
					+ (1 - u) * v * src.at<Vec3b>(i1, j2)[2]
					+ u * (1 - v) * src.at<Vec3b>(i2, j1)[2]
					+ u * v * src.at<Vec3b>(i2, j2)[2];
			}
		}
	}
}

四.旋转

1.一般图像的旋转是以图像的中心为原点，将图像上的所有像素都旋转一个相同的角度。
2.图像的旋转变换是图像的位置变换，但旋转后，图像的大小一般会改变。
3.图像旋转变换后，既可以把转出显示区域的图像截去，也可以扩大图像范围以显示所有的图像。
4.变换矩阵
在这里插入图片描述
在这里插入图片描述

//图像旋转
void img_rotate(Mat& src, Mat& dst, double Angle)
{
	double angle = Angle * CV_PI / 180.0;
	//构造输出图形
	int dst_rows = (int)round(fabs(src.rows * cos(angle)) + fabs(src.cols * sin(angle)));//图像高度
	int dst_cols = (int)round(fabs(src.cols * cos(angle)) + fabs(src.rows * sin(angle)));//图像宽度
	dst.create(dst_rows, dst_cols, src.type());

	//将原图像坐标映射到数学笛卡尔坐标
	Mat T1 = (Mat_<double>(3, 3) << 1.0, 0.0, 0.0, 0.0, -1.0, 0.0, -0.5 * src.cols, 0.5 * src.rows, 1.0);
	//数学笛卡尔坐标下顺时针旋转的变换矩阵
	Mat T2 = (Mat_<double>(3, 3) << cos(angle), -sin(angle), 0.0, sin(angle), cos(angle), 0.0, 0.0, 0.0, 1.0);
	//将数学笛卡尔坐标映射到旋转后的图像坐标
	double t3[3][3] = { {1.0,0.0,0.0},{0.0,-1.0,0.0},{0.5 * dst.cols,0.5 * dst.rows,1.0} };
	Mat T3 = Mat(3.0, 3.0, CV_64FC1, t3);
	Mat T = T1 * T2 * T3;
	Mat T_inv = T.inv();    //求逆矩阵

	for (double i = 0.0; i < dst.rows; i++)
	{
		for (double j = 0.0; j < dst.cols; j++)
		{
			Mat dst_coordinate = (Mat_<double>(1, 3) << j, i, 1.0);
			Mat src_coordinate = dst_coordinate * T_inv;
			double v = src_coordinate.at<double>(0, 0);   //原图像的横坐标，列，宽
			double w = src_coordinate.at<double>(0, 1);  //原图像的纵坐标，行，高

			//判断是否越界
			if (int(Angle) % 90 == 0)
			{
				if (v < 0)
				{
					v = 0;
				}
				if (v > src.cols - 1)
				{
					v = src.cols - 1;
				}
				if (w < 0)
				{
					w = 0;
				}
				if (w > src.rows - 1)
				{
					w= src.rows - 1;
				}
			}

			if (v >= 0 && w >= 0 && v < src.cols - 1 && w <= src.rows - 1)
			{
				int top = floor(w), bottom = ceil(w), left = floor(v), right = ceil(v);
				double pw = w - top;   //pw为坐标 行 的小数部分
				double pv = v - left;  //pv为坐标 列 的小数部分
				if (src.channels() == 1)
				{
					//灰度图像
					dst.at<uchar>(i, j) = (1 - pw) * (1 - pv) * src.at<uchar>(top, left)
						+ (1 - pw) * pv * src.at<uchar>(top, right)
						+ pw * (1 - pv) * src.at<uchar>(bottom, left)
						+ pw * pv * src.at<uchar>(bottom, right);
				}
				else
				{
					//彩色图像
					dst.at<Vec3b>(i, j)[0] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[0]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[0]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[0]
						+ pw * pv * src.at<Vec3b>(bottom, right)[0];
					dst.at<Vec3b>(i, j)[1] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[1]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[1]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[1]
						+ pw * pv * src.at<Vec3b>(bottom, right)[1];
					dst.at<Vec3b>(i, j)[2] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[2]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[2]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[2]
						+ pw * pv * src.at<Vec3b>(bottom, right)[2];
				}
			}
		}
	}
}

五.镜像

1.水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心进行镜像对换。
2.垂直镜像操作是将图片上半部分和下半部分以图像水平中轴线为中心进行镜像对换。
在这里插入图片描述
3.变换矩阵
在这里插入图片描述

六.复合变换

1.图像的复合变换是指对给定的图像连续施行若干次如前所述的平移、镜像、比例缩放、旋转等基本操作后所完成的变换，图像的复合变换又叫级联变换。
2.利用齐次坐标，对给定的图像依次按一定顺序连续施行若干次基本变换，其变换的矩阵仍可以用3×3阶的矩阵表示。复合变换的矩阵等于基本变换的矩阵按顺序依次相乘得到的组合矩阵。
3.设对给定的图像依次进行了基本变换F1,F2,…,FN，他们的变换矩阵分别为T1,T2,…TN，按照几何变换公式的表示形式，图像复合变换的矩阵T可以表示为：T=TNTN-1···T1。

七.变换矩阵总结

在这里插入图片描述

八.完整代码

#include<opencv2/core.hpp>
#include<opencv2/highgui.hpp>
#include<iostream>
#include<opencv2/highgui/highgui.hpp>
#include<opencv2/imgproc/imgproc.hpp>
#include<opencv2/imgproc/types_c.h>

using namespace cv;
using namespace std;

//最近邻差值缩放
void nearest(Mat& src, Mat& dst, float sx, float sy)  //原图，处理后图，x方向倍数，y方向倍数
{
	//round函数计算之后结果是小数点后全变为0，但其还是float的，需要强制类型转换
	//计算目标图形尺寸
	int dst_cols = (int)round(src.cols * sx);
	int dst_rows = (int)round(src.rows * sy);
	//创建目标图形
	dst.create(dst_rows, dst_cols, src.type());
	//灰度图像处理
	if (src.channels() == 1)
	{
		for (int i = 0; i < dst.rows; i++)
		{
			for (int j = 0; j < dst.cols; j++)
			{
				//插值计算，输出图像的像素点由原图像对应的最近的像素点得到（四舍五入）
				int i_index = (int)round(i / sy);    //y方向缩放，则行数发生改变
				int j_index = (int)round(j / sx);
				//防止越界
				if (i_index > src.rows - 1)
				{
					i_index = src.rows - 1;
				}
				if (j_index > src.cols - 1)
				{
					j_index = src.cols - 1;
				}
				dst.at<uchar>(i, j) = src.at<uchar>(i_index, j_index);
			}
		}
	}
	//彩色图像处理
	else
	{
		for (int i = 0; i < dst.rows; i++)
		{
			for (int j = 0; j < dst.cols; j++)
			{
				//差值计算
				int i_index = (int)round(i / sy);
				int j_index = (int)round(j / sx);
				//防止越界
				if (i_index > src.rows - 1)
				{
					i_index = src.rows - 1;
				}
				if (j_index > src.cols - 1)
				{
					j_index = src.cols - 1;
				}
				//b
				dst.at<Vec3b>(i, j)[0] = src.at<Vec3b>(i_index, j_index)[0];
				//g
				dst.at<Vec3b>(i, j)[1] = src.at<Vec3b>(i_index, j_index)[1];
				//r
				dst.at<Vec3b>(i, j)[2] = src.at<Vec3b>(i_index, j_index)[2];
			}
		}
	}
}

//双线性插值缩放
//对于一个目的像素，设置坐标通过反向变换得到的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分，
//u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个像素得值 f(i+u,j+v) 可由原图像中坐标为
//(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定，即：
//f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) 
//其中f(i, j)表示源图像(i, j)处的的像素值，以此类推。
void linear(Mat& src, Mat& dst, float sx, float sy)
{
	//计算目标图形尺寸
	int dst_cols = (int)round(src.cols * sy);
	int dst_rows = (int)round(src.rows * sx);
	//创建目标图形
	dst.create(dst_rows, dst_cols, src.type());
	for (int i = 0; i < dst.rows; i++)
	{
		//几何中心对齐
		//中心对齐(OpenCV也是如此)：
			//SrcX = (dstX + 0.5) * (srcWidth / dstWidth) - 0.5
			//SrcY = (dstY + 0.5) * (srcHeight / dstHeight) - 0.5
		double index_i = (i + 0.5) / sx - 0.5;
		//防止越界
		if (index_i < 0)
		{
			index_i = 0;
		}
		if (index_i >= (double)src.rows - 1)
		{
			index_i = (double)src.rows - 2;
		}
		//相邻4×4像素的行（坐标）
		int i1 = floor(index_i);
		int i2 = ceil(index_i);
		//u为得到浮点型坐标的小数部分
		double u = index_i - i1;
		for (int j = 0; j < dst.cols; j++)
		{
			//几何中心对齐
			double index_j = (j + 0.5) / sy - 0.5;
			//防止越界
			if (index_j < 0)
			{
				index_j = 0;
			}
			if (index_j >= (double)src.cols - 1)
			{
				index_j = (double)src.cols - 2;
			}
			//相邻4×4像素的列（坐标）
			int j1 = floor(index_j);
			int j2 = ceil(index_j);
			//u为得到浮点型坐标的小数部分
			double v = index_j - j1;
			//处理灰度图像
			if (src.channels() == 1)
			{
				dst.at<uchar>(i, j) = (1 - u) * (1 - v) * src.at<uchar>(i1, j1)
					+ (1 - u) * v * src.at<uchar>(i1, j2)
					+ u * (1 - v) * src.at<uchar>(i2, j1)
					+ u * v * src.at<uchar>(i2, j2);
			}
			//处理彩色图像
			else
			{
				dst.at<Vec3b>(i, j)[0] = (1 - u) * (1 - v) * src.at<Vec3b>(i1, j1)[0] 
					+ (1 - u) * v * src.at<Vec3b>(i1, j2)[0]
					+ u * (1 - v) * src.at<Vec3b>(i2, j1)[0] 
					+ u * v * src.at<Vec3b>(i2, j2)[0];
				dst.at<Vec3b>(i, j)[1] = (1 - u) * (1 - v) * src.at<Vec3b>(i1, j1)[1] 
					+ (1 - u) * v * src.at<Vec3b>(i1, j2)[1] 
					+ u * (1 - v) * src.at<Vec3b>(i2, j1)[1] 
					+ u * v * src.at<Vec3b>(i2, j2)[1];
				dst.at<Vec3b>(i, j)[2] = (1 - u) * (1 - v) * src.at<Vec3b>(i1, j1)[2]
					+ (1 - u) * v * src.at<Vec3b>(i1, j2)[2]
					+ u * (1 - v) * src.at<Vec3b>(i2, j1)[2]
					+ u * v * src.at<Vec3b>(i2, j2)[2];
			}
		}
	}
}

//图像旋转
void img_rotate(Mat& src, Mat& dst, double Angle)
{
	double angle = Angle * CV_PI / 180.0;
	//构造输出图形
	int dst_rows = (int)round(fabs(src.rows * cos(angle)) + fabs(src.cols * sin(angle)));//图像高度
	int dst_cols = (int)round(fabs(src.cols * cos(angle)) + fabs(src.rows * sin(angle)));//图像宽度
	dst.create(dst_rows, dst_cols, src.type());

	//将原图像坐标映射到数学笛卡尔坐标
	Mat T1 = (Mat_<double>(3, 3) << 1.0, 0.0, 0.0, 0.0, -1.0, 0.0, -0.5 * src.cols, 0.5 * src.rows, 1.0);
	//数学笛卡尔坐标下顺时针旋转的变换矩阵
	Mat T2 = (Mat_<double>(3, 3) << cos(angle), -sin(angle), 0.0, sin(angle), cos(angle), 0.0, 0.0, 0.0, 1.0);
	//将数学笛卡尔坐标映射到旋转后的图像坐标
	double t3[3][3] = { {1.0,0.0,0.0},{0.0,-1.0,0.0},{0.5 * dst.cols,0.5 * dst.rows,1.0} };
	Mat T3 = Mat(3.0, 3.0, CV_64FC1, t3);
	Mat T = T1 * T2 * T3;
	Mat T_inv = T.inv();    //求逆矩阵

	for (double i = 0.0; i < dst.rows; i++)
	{
		for (double j = 0.0; j < dst.cols; j++)
		{
			Mat dst_coordinate = (Mat_<double>(1, 3) << j, i, 1.0);
			Mat src_coordinate = dst_coordinate * T_inv;
			double v = src_coordinate.at<double>(0, 0);   //原图像的横坐标，列，宽
			double w = src_coordinate.at<double>(0, 1);  //原图像的纵坐标，行，高

			//判断是否越界
			if (int(Angle) % 90 == 0)
			{
				if (v < 0)
				{
					v = 0;
				}
				if (v > src.cols - 1)
				{
					v = src.cols - 1;
				}
				if (w < 0)
				{
					w = 0;
				}
				if (w > src.rows - 1)
				{
					w= src.rows - 1;
				}
			}

			if (v >= 0 && w >= 0 && v < src.cols - 1 && w <= src.rows - 1)
			{
				int top = floor(w), bottom = ceil(w), left = floor(v), right = ceil(v);
				double pw = w - top;   //pw为坐标 行 的小数部分
				double pv = v - left;  //pv为坐标 列 的小数部分
				if (src.channels() == 1)
				{
					//灰度图像
					dst.at<uchar>(i, j) = (1 - pw) * (1 - pv) * src.at<uchar>(top, left)
						+ (1 - pw) * pv * src.at<uchar>(top, right)
						+ pw * (1 - pv) * src.at<uchar>(bottom, left)
						+ pw * pv * src.at<uchar>(bottom, right);
				}
				else
				{
					//彩色图像
					dst.at<Vec3b>(i, j)[0] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[0]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[0]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[0]
						+ pw * pv * src.at<Vec3b>(bottom, right)[0];
					dst.at<Vec3b>(i, j)[1] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[1]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[1]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[1]
						+ pw * pv * src.at<Vec3b>(bottom, right)[1];
					dst.at<Vec3b>(i, j)[2] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[2]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[2]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[2]
						+ pw * pv * src.at<Vec3b>(bottom, right)[2];
				}
			}
		}
	}
}

//平移变换
//tx:水平平移距离，正数向右移动，负数向左移动
//ty:垂直平移距离，正数向下移动，负数向上移动
void trans(Mat& src, Mat& dst, double tx, double ty)
{
	//创建输出图像
	dst.create(src.size(), src.type());
	//平移变换矩阵
	Mat T = (Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, tx, ty, 1);
	//求逆矩阵
	Mat T_inv = T.inv();

	for (int i = 0; i < dst.rows; i++)
	{
		for (int j = 0; j < dst.cols; j++)
		{
			Mat dst_coordinate = (Mat_<double>(1, 3) << j, i, 1);
			Mat src_coordinate = dst_coordinate * T_inv;
			double v = src_coordinate.at<double>(0, 0);  //原图像的横坐标，列，宽
			double w = src_coordinate.at<double>(0, 1);  //原图像的纵坐标，行，高

			if (v >= 0 && w >= 0 && v < src.cols - 1 && w <= src.rows - 1)
			{
				int top = floor(w), bottom = ceil(w), left = floor(v), right = ceil(v);
				double pw = w - top;   //pw为坐标 行 的小数部分
				double pv = v - left;  //pv为坐标 列 的小数部分
				if (src.channels() == 1)
				{
					//灰度图像
					dst.at<uchar>(i, j) = (1 - pw) * (1 - pv) * src.at<uchar>(top, left)
						+ (1 - pw) * pv * src.at<uchar>(top, right)
						+ pw * (1 - pv) * src.at<uchar>(bottom, left)
						+ pw * pv * src.at<uchar>(bottom, right);
				}
				else
				{
					//彩色图像
					dst.at<Vec3b>(i, j)[0] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[0]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[0]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[0]
						+ pw * pv * src.at<Vec3b>(bottom, right)[0];
					dst.at<Vec3b>(i, j)[1] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[1]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[1]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[1]
						+ pw * pv * src.at<Vec3b>(bottom, right)[1];
					dst.at<Vec3b>(i, j)[2] = (1 - pw) * (1 - pv) * src.at<Vec3b>(top, left)[2]
						+ (1 - pw) * pv * src.at<Vec3b>(top, right)[2]
						+ pw * (1 - pv) * src.at<Vec3b>(bottom, left)[2]
						+ pw * pv * src.at<Vec3b>(bottom, right)[2];
				}
			}

		}
	}

}
int main()
{
	Mat src = imread("cat.webp");
	
	//图像的缩放
	Mat dst1,dst2;
	//使用函数resize
	dst1 = Mat::zeros(812, 612, CV_8UC3);    //放大
	dst2 = Mat::zeros(200, 300, CV_8UC3);    //缩小
	resize(src, dst1, dst1.size());
	resize(src, dst2, dst2.size());
	//使用像素矩阵
	float sx0 = 3.0f, sy0 = 2.0f;    //放大的倍数
	float sx1 = 0.4f, sy1 = 0.6f;     //缩小的倍数
	//在 C 语言中，如果不指定数据类型，那么小数常量会被认为是 double 类型的
	//由于它是常量，所以编译器称为 const double。
	//double 是不能隐式转换为 float 的。
	//在后面加一个f或F，且需写成小数形式
	//最近邻插值放大缩小
	Mat dst3, dst4;
	nearest(src, dst3, sx0, sy0);
	nearest(src, dst4, sx1, sy1);
	//双线性插值
	Mat dst5, dst6;
	linear(src, dst5, sx0, sy0);
	linear(src, dst6, sx1, sy1);

	//旋转
	Mat dst7;
	img_rotate(src, dst7, 250);

	//平移
	Mat dst8;
	trans(src, dst8, 80.11, 100.33);

	imshow("原图", src);
	imshow("调用函数-放大", dst1);
	imshow("调用函数-缩小", dst2);
	imshow("最近邻插值-放大", dst3);
	imshow("最近邻插值-缩小", dst4);
	imshow("双线性插值-放大", dst5);
	imshow("双线性插值-缩小", dst6);
	imshow("旋转250", dst7);
	imshow("平移", dst8);
	cout << "size:" << src.size() << endl;
	cout << "row:" << src.rows << endl;
	cout << "col:" << src.cols << endl;
	waitKey(0);
	return 0;
}

参考文章：https://blog.csdn.net/weixin_40647819/article/details/87912122

CG3-v2.0-图形几何变换
Junds0的博客
09-23 1880
(1) 理解几何变换基本原理, 掌握平移、旋转、缩放变换的方法; (2) 根据平移算法原理补全translation、scale、rotation_x、rotation_y和rotation_z函数; (3) 根据几何变换基本原理,将main函数中的translation、scale、rotation_z参数补充完整。 第2关：图形的平移与缩放 (1) 理解几何变换基本原理, 掌握平移和缩放变换的方法; (2) 根据几何变换基本原理,将main函数中的空白部分补充完整。 第3关：图形的平移与旋转 (1) 理
[Python从零到壹] 三十八.图像处理基础篇之图像几何变换（平移缩放旋转）
热门推荐
杨秀璋的专栏
01-27 1万+
欢迎大家来到“Python从零到壹”，在这里我将分享约200篇Python系列文章，带大家一起去学习和玩耍。上一篇文章介绍了图像融合处理和ROI区域绘制，同时补充图像属性、通道和类型转换。这篇文章将详细讲解图像几何变换，包括图像平移、图像缩放和图像旋转。希望文章对您有所帮助，如果有不足之处，还请海涵。
头歌实践教学平台：CG3-v2.0-图形几何变换
菜鸟的博客~
05-08 963
(2) 根据平移算法原理补全translation、scale、rotation_x、rotation_y和rotation_z函数;(3) 将立方体的顶点坐标分别向x,y,z轴正方向平移0.5个单位距离，然后绘制一个红色正方形；(4) 将立方体的顶点坐标分别沿x,y,z轴方向缩放0.5倍，然后绘制一个绿色正方形；时，物体x、y坐标改变，而z坐标值在该变换中不改变，即。时，物体y、z坐标改变，而x坐标值在该变换中不改变，即。时，物体x、z坐标改变，而y坐标值在该变换中不改变，即。开始你的任务吧，祝你成功！
图像的几何变换
最新发布
qq_53529450的博客
03-25 641
本文全面探讨了图像几何变换在计算机视觉和图像处理中的重要性，涵盖其数学基础、应用场景及对图像信息的影响。几何变换通过变换矩阵（如平移、旋转、缩放）实现，采用齐次坐标和矩阵乘法组合复杂操作。应用包括数据增强（提升深度学习模型鲁棒性）、图像注册（医学与遥感对齐）、视图变换（计算机图形学）等。变换可能导致信息保留或丢失，影响特征分布，同时增强CNN和GAN的性能。文章详细分析了平移（矩阵表示、边界处理）和旋转（公式、插值方法如最近邻、双线性、双三次）的原理与应用，强调其在图像拼接、视觉效果及特征提取中的作用。
几何变换详解
weixin_34106122的博客
08-08 590
在三维图形学中，几何变换大致分为三种，平移变换（Translation），缩放变换（Scaling），旋转变换（Rotation）。以下讨论皆针对DirectX，所以使用左手坐标系。 平移变换 将三维空间中的一个点[x, y, z, 1]移动到另外一个点[x', y', z', 1]，三个坐标轴的移动分量分别为dx=Tx, dy=Ty, dz=Tz, 即 x' = x + Tx y' = ...
图像的几何变换—平移、旋转、镜像、缩放、剪切（原理+调用函数+像素操作）
☆下山☆的博客
10-10 5259
图像的几何变换—平移、旋转、镜像、缩放、剪切（原理+调用函数+像素操作）
头歌-图形扩展缩放、平移、旋转
f3244077856的博客
11-01 926
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), 45, 0.6) # 旋转中心，旋转角度，缩放因子,这里缩放因子的作用是变为原来的0.6倍。cv2.warpAffine 接收的参数是2 × 3 的变换矩阵，而 cv2.warpPerspective 接收的参数是 3 × 3 的变换矩阵。M = np.float32([[1, 0, 30], [0, 1, 60]]) # 构建移动矩阵,x轴左移30个像素，y轴下移60个。
几何变换
君只见独不见的专栏
04-30 595
几何变换详解 在三维图形学中，几何变换大致分为三种，平移变换（Translation），缩放变换（Scaling），旋转变换（Rotation）。以下讨论皆针对DirectX，所以使用左手坐标系。 平移变换 将三维空间中的一个点[x, y, z, 1]移动到另外一个点[x’, y’, z’, 1]，三个坐标轴的移动分量分别为dx=Tx, dy=Ty, dz=Tz, 即 x’ = x + Tx y’...
Python3+OpenCV2实现图像的几何变换(平移、镜像、缩放、旋转、仿射)
01-01
总结一下最近看的关于opencv图像几何变换的一些笔记. 这是原图: 1.平移 import cv2 import numpy as np img = cv2.imread(image0.jpg, 1) imgInfo = img.shape height = imgInfo[0] width = imgInfo[1] mode =...
几何变换 图像平移 垂直镜像 水平镜像 图像转置 图像缩放 图像旋转.rar
09-07
本项目基于VS2017开发，提供了一组完整的图像处理功能，包括图像平移、垂直镜像、水平镜像、图像转置和图像缩放以及图像旋转。下面我们将详细讨论这些知识点。 1. **图像平移**：图像平移是指将图像在二维空间中...
MFC 图像处理之几何运算 图像平移旋转缩放镜像(源码)
06-04
该资源主要参考我的博客【数字图像处理】六.MFC空间几何变换之图像平移、镜像、旋转、缩放详解，博客地址http://blog.csdn.net/eastmount/article/details/46345299 主要讲述基于VC++6.0 MFC图像处理的应用知识，要...
几何变换(图像平移,，垂直镜像，水平镜像，图像转置，缩放，旋转）
04-21
几何变换(图像平移,，垂直镜像，水平镜像，图像转置，缩放，旋转）
几何变换.docx
06-21
仿射变换平移，缩放，旋转原理
36.OpenCV图像几何变换万字详解（平移缩放旋转、镜像仿射透视）.pdf
03-31
根据变换的复杂程度，可以将其大致分为简单变换（如平移、缩放、旋转、镜像）和复杂变换（如仿射变换、透视变换）。接下来，我们将详细介绍这些变换的基本原理和OpenCV中的实现方法。 ### 一、图像平移变换 #### ...
简单几何变换
FH的博客
05-26 833
简单几何变换几何表示2D几何变换translation 平移rotation+transform （平移+旋转）刚性变换Similarity相似变换(旋转+按比缩放+平移)Affine放射变换projective 投影影变换(透视变换、同态映射)3D几何变换 几何变换就是空间变换，是图形学的基础算法，在计算机视觉中应用也比较广泛。本文就简单介绍集中基础几何变换 几何表示 2D几何变换 “名场面”如...
头歌cg3-v2.0-图形几何变换
10-25
头歌cg3-v2.0-图形几何变换是一种计算机图形处理技术，可以对图形进行各种几何变换，如平移、旋转、缩放和投影等。该技术广泛应用在图形设计、游戏开发和虚拟现实等领域。 平移是指将图形沿着某个方向进行移动，不改变其形状和大小。通过指定平移的距离和方向，可以将图形在二维或三维空间中进行移动。平移可以用于实现物体的移动、拖拽和动画效果。 旋转是指将图形绕着某个中心点进行旋转。通过指定旋转的角度和旋转中心，可以使图形围绕指定中心点进行旋转。旋转可以用于实现物体的旋转效果、转盘等视觉效果。 缩放是指改变图形的大小，可以放大或缩小图形。通过指定缩放的比例因子，可以按照指定比例对图形进行放大或缩小。缩放可以用于实现物体的大小调整、变焦效果等。 投影是指将图形从三维空间映射到二维平面上。通过指定投影的参数，可以将三维图形投影到二维平面上呈现出逼真的视觉效果。投影可以用于实现三维场景的渲染和显示。 头歌cg3-v2.0-图形几何变换技术可以大大提高图形处理的效率和质量，使得图形在虚拟环境中更加真实和逼真。它为图形设计师、游戏开发者和虚拟现实应用提供了强大的工具和技术支持，帮助他们创造出更加优秀的作品。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

llurran

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值