Swin Transformer 时间复杂度的分析

Swin Transformer的论文中涉及到了两个关于时间复杂度的计算公式，在此梳理一下推导过程。

1. 前置知识

神经网络的运算过程中涉及大量矩阵运算，因此在分析时间复杂度之前，需要对矩阵运算的复杂度有一个基本的认识，假设有三个矩阵$A\in {\mathbb{R}}^{m\times n}$，$B\in {\mathbb{R}}^{n\times l}$，$C\in {\mathbb{R}}^{l\times m}$：
$$\Theta (AB)=O(mln)$$$$\Theta (ABC)=O(mln)+O(m^{2}l)$$
可以理解为：第一个矩阵的行维（第一维）$\times$ 第二个矩阵的列维（第二维）$\times$ 两个矩阵的相等维度。三个矩阵的情况需要先计算前两个，根据计算结果和第三个矩阵的维度就可以计算整体的复杂度。

2. Transformer的时间复杂度

Transformer是2017由Google提出的用于NLP领域的自注意力模型，其核心模块则是Multi-Head Self-Attention（MSA）：

假设序列长度为$L$，词向量维度为$C$，所以输入的形状是$[batchsize,L,C]$。在计算时间复杂度时暂时忽略batch size，而多头各自计算并不影响结果，所以也可以忽略。

MSA可以分为四个阶段：

1. Q, K, V分别进行了Linear变换，每个都可以看成是$[L,C]\times [C,C]$ ，时间复杂度：$L{C}^2+L{C}^2+L{C}^2=3L{C}^2$
2. dot-product的$Q{K}^{\top }$，$[L,C]\times [C,L]$，时间复杂度：$L^{2}C$
3. Softmax操作后与$V$相乘，$[L,L]\times [L,C]$，时间复杂度：$L^{2}C$
4. Attention最后的Linear层，$[L,C]\times [C,C]$，时间复杂度：$L{C}^2$

四个阶段相加，得到最终的时间复杂度$4L{C}^2+2L^{2}C$

3. Vision Transformer的时间复杂度

Vision Transformer提出了Patch Embedding的思想：

Transformer的时间复杂度为$4L{C}^2+2L^{2}C$。如上图所示，在ViT中，$L$ = Patch的个数 = $9$，$C$ = 每个Patch的Depth = Embedding的维度，这个Depth类似CNN中的output channel。假设图像在Patch后的宽度为$w$，高度为$h$，则：
$$L=w\times h=3\times 3=9$$
因此，ViT的时间复杂度可以表示为：
$$\Theta (MSA)=4L{C}^2+2L^{2}C=4(hw)C^2+2(hw{)}^{2}C$$
这与Swin Transformer论文中所列的结果一致，时间复杂度与$hw$呈平方相关。

4. Swin Transformer的时间复杂度

Swin Transformer沿用了Patch的设定，但为了进一步降低时间复杂度，在此基础上提出了Window的思想。

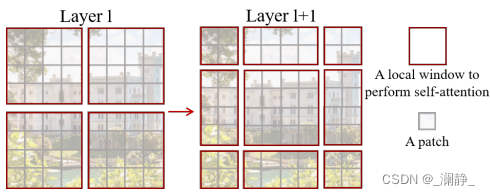
如下图所示，Swin Transformer Block的时间复杂度集中于W-MSA与SW-MSA。SW-MSA比W-MSA多了一来一回两步平移操作，和一步Mask操作，但是二者的计算量依然是同一个量级。

假设Window的边长为$M$，则大小为$M\times M$。如第一张图中的Layer 1所示，在W-MSA中，所有的patch被划分为 $\frac{h}{M}\times \frac{w}{M}$ 个Windows，每个Window单独做self-attention的Q, K, V运算。把$M$带入，每个Window的时间复杂度为：
$$\Theta (Window)=4M^2{C}^2+2M^{4}C$$
因此，整个W-MSA的时间复杂度可以表示为：
$$\Theta (W-MSA)=(4M^2{C}^2+2M^{4}C)\times (\frac{h}{M}\times \frac{w}{M})=4hw{C}^2+2M^{2}hwC$$
推导结果与论文中的保持一致，时间复杂度降到与$hw$呈线性相关，至此推导完毕。

在论文后半部的实验也证明，Swin相比于ViT很大幅度地降低了计算时间。