matlab和python仿真实现吉布斯抽样，简单的二维分布抽样

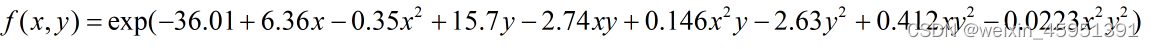
通过函数进行Gibbs采样，该函数定义了一个二维分布。代码首先将函数归一化，使其在x从0到20、y从0到2π的范围内积分为1。然后执行Gibbs采样并绘制生成的样本。

python代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import dblquad

# 定义所提供的函数
def f(x, y):
    return np.exp(-36.01 + 6.36*x - 0.35*x**2 + 15.7*y - 2.74*x*y + 0.146*x**2*y - 2.63*y**2 + 0.412*x*y**2 - 0.0223*x**2*y**2)

# 积分范围
x_bounds = (0, 20)
y_bounds = (0, 2*np.pi)

# 将函数归一化，使其在指定范围内积分为1
integral, error = dblquad(f, x_bounds[0], x_bounds[1], lambda x: y_bounds[0], lambda x: y_bounds[1])
norm_factor = 1 / integral

# Gibbs采样函数
def gibbs_sampling(f, n_samples, x_bounds, y_bounds, norm_factor):
    samples = np.zeros((n_samples, 2))
    x_current = np.random.uniform(x_bounds[0], x_bounds[1])
    y_current = np.random.uniform(y_bounds[0], y_bounds[1])

    for i in range(n_samples):
        # 从给定y的x的条件分布中采样
        x_pdf = lambda x: f(x, y_current) * norm_factor
        x_samples = np.linspace(x_bounds[0], x_bounds[1], 1000)
        x_probs = np.array([x_pdf(val) for val in x_samples])
        x_probs /= np.sum(x_probs)
        x_current = np.random.choice(x_samples, p=x_probs)

        # 从给定x的y的条件分布中采样
        y_pdf = lambda y: f(x_current, y) * norm_factor
        y_samples = np.linspace(y_bounds[0], y_bounds[1], 1000)
        y_probs = np.array([y_pdf(val) for val in y_samples])
        y_probs /= np.sum(y_probs)
        y_current = np.random.choice(y_samples, p=y_probs)

        samples[i, :] = [x_current, y_current]

    return samples

# 要生成的样本数
n_samples = 1000

# 进行Gibbs采样
samples = gibbs_sampling(f, n_samples, x_bounds, y_bounds, norm_factor)

# 绘制生成的样本
plt.figure(figsize=(10, 6))
plt.scatter(samples[:, 0], samples[:, 1], alpha=0.5, s=1)
plt.xlim(x_bounds)
plt.ylim(y_bounds)
plt.xlabel('x')
plt.ylabel('y')
plt.title('使用Gibbs采样的二维分布样本')
plt.show()

 仿真结果：

matlab代码：

function samples = gibbs_sampling(f, n_samples, x_bounds, y_bounds, norm_factor)
    samples = zeros(n_samples, 2);
    x_current = (x_bounds(2) - x_bounds(1)) * rand() + x_bounds(1);
    y_current = (y_bounds(2) - y_bounds(1)) * rand() + y_bounds(1);

    for i = 1:n_samples
        % 从给定y的x的条件分布中采样
        x_pdf = @(x) f(x, y_current) * norm_factor;
        x_samples = linspace(x_bounds(1), x_bounds(2), 1000);
        x_probs = arrayfun(x_pdf, x_samples);
        x_probs = x_probs / sum(x_probs);
        x_current = randsample(x_samples, 1, true, x_probs);

        % 从给定x的y的条件分布中采样
        y_pdf = @(y) f(x_current, y) * norm_factor;
        y_samples = linspace(y_bounds(1), y_bounds(2), 1000);
        y_probs = arrayfun(y_pdf, y_samples);
        y_probs = y_probs / sum(y_probs);
        y_current = randsample(y_samples, 1, true, y_probs);

        samples(i, :) = [x_current, y_current];
    end
end

% 定义所提供的函数
f = @(x, y) exp(-36.01 + 6.36*x - 0.35*x.^2 + 15.7*y - 2.74*x.*y + 0.146*x.^2.*y - 2.63*y.^2 + 0.412*x.*y.^2 - 0.0223*x.^2.*y.^2);

% 积分范围
x_bounds = [0, 20];
y_bounds = [0, 2*pi];

% 使用数值方法计算积分以归一化函数
integral = integral2(f, x_bounds(1), x_bounds(2), y_bounds(1), y_bounds(2));
norm_factor = 1 / integral;

% 要生成的样本数
n_samples = 1000;

% 进行Gibbs采样
samples = gibbs_sampling(f, n_samples, x_bounds, y_bounds, norm_factor);

% 绘制生成的样本
scatter(samples(:, 1), samples(:, 2), '.');
xlim(x_bounds);
ylim(y_bounds);
xlabel('x');
ylabel('y');
title('使用Gibbs采样的二维分布样本');

 运行结果