10 最大期望(EM)

Expectation Maximization (EM) 算法，中文名字叫做“期望最大”算法，是用来解决具有隐变量的混合模型的参数估计（即其极大似然估计）。在比较简单的情况中，我们可以直接得出我们想要求得的参数的解析解，比如：MLE: $p(X|\theta )$。我们想要求解的结果就是： $${\theta }_{MLE}=\underset{\theta }{\mathrm{argmax}}\log p(X|\theta )$$其中，$logp(X|\theta )$ 也被我们称为对数似然函数。一旦问题变得复杂起来以后，就不是这么简单了，特别是引入了隐变量之后。

最大似然MLE和最大后验MAP的关系？
$\theta$ 和隐变量 Z 的关系？$\theta$ 是否可以看作隐变量？

1 EM 算法简述以及收敛性证明

1.1 EM 算法简述

实际上，EM 算法的描述也并不是很难，我们知道，通常我们想求的似然函数为 $p(X|\theta )$。引入隐变量之后，原式就变成了： $$p(X|\theta )=\int p(X,Z|\theta )p\left(Z|X,{\theta }^{(t)}\right)dZ$$EM 算法是一种迭代的算法，我们的目标是求：
$${\theta }^{t+1}=\underset{\theta }{\mathrm{argmax}}{\int }_Z\log [p(X,Z|\theta )]p(Z|X,{\theta }^t)dZ={\mathbb{E}}_{Z|X,{\theta }^t}[\log p(X,Z|\theta )]$$也就是找到一个更新的参数 $\theta$，使得 $p(X,Z|\theta )$ 出现的概率更大。

1.2 EM 算法的收敛性

我们想要证明的是当 ${\theta }^{(t)}⟶{\theta }^{(t+1)}$ 时，有 $\log p\left(X|{\theta }^{(t)}\right)\le \log p\left(X|{\theta }^{(t+1)}\right)$，这样才能说明我们的每次迭代都是有效的，也就是每次迭代都要使 $X$ 发生的概率增加。
$$\log p(X|\theta )=\log \frac{p(X,Z|\theta )}{p(Z|X;\theta )}=\log p(X,Z|\theta )-\log p(Z|X;\theta )$$下一步，则是同时对两边求关于 $p(X,Z|{\theta }^{(t)})$的期望。
左边：
$$\begin{array}{rl}{\mathbb{E}}_{Z\sim p\left(Z|X,{\theta }^{(t)}\right)}[\log p(X|\theta )]& ={\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log p(X|\theta )dZ.\\ & =\log p(X|\theta ){\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)dZ\\ & =\log p(X|\theta )\cdot 1=\log p(X|\theta )\end{array}$$
右边：
$$\underset{Q\left(\theta ,{\theta }^{(t)}\right)}{\underbrace{{\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log p(X,Z|\theta )dZ}}-\underset{H\left(\theta ,{\theta }^{(t)}\right)}{\underbrace{{\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log p(Z|X,\theta )dZ}}$$

所以：
$$\log p(X|\theta )=Q(\theta ,{\theta }^t)-H(\theta ,{\theta }^t)$$
由于 $Q(\theta ,{\theta }^t)={\int }_{Z}p(Z|X,{\theta }^t)\log p(X,Z|\theta )dZ$，而 ${\theta }^{t+1}=\underset{\theta }{\mathrm{argmax}}{\int }_Z\log [p(X,Z|\theta )]p(Z|X,{\theta }^t)dZ$，所以 $Q({\theta }^{t+1},{\theta }^t)\ge Q({\theta }^t,{\theta }^t)$。

要证 $$\begin{gathered} \log p(x|{\theta }^t)\le \\ logp(x|{\theta }^{t+1}) \end{gathered}$$，还需证： $H({\theta }^t,{\theta }^t)\ge H({\theta }^{t+1},{\theta }^t)$：
$$\begin{array}{rl}H\left({\theta }^{(t+1)},{\theta }^{(t)}\right)-H\left({\theta }^{(t)},{\theta }^{(t)}\right)& ={\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log p\left(Z|X,{\theta }^{(t+1)}\right)dZ-{\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log p\left(Z|X,{\theta }^{(t)}\right)dZ\\ & ={\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log \frac{p\left(Z|X,{\theta }^{(t+1)}\right)}{p\left(Z|X,{\theta }^{(t)}\right)}dZ\\ & =-KL\left(p\left(Z|X,{\theta }^{(t)}\right)\Vert p\left(Z|X,{\theta }^{(t+1)}\right)\right)\le 0\end{array}$$

为什么Q不用KL？答：关于Q的比较，属于定义部分，本节第二个公式。

或者，我们也可以使用Jensen inequality。很显然，log 函数是一个concave 函数（凸函数），那么有 $E[logX]\le log[E[X]]$，那么：
$$\begin{array}{rl}{\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\log \frac{p\left(Z|X,|{\theta }^{(t+1)}\right)}{p\left(Z|X,{\theta }^{(t)}\right)}dZ& ={\mathbb{E}}_{Z\sim p\left(Z|X,{\theta }^{(t)}\right)}\left[\log \frac{p\left(Z|X,{\theta }^{(t+1)}\right)}{p\left(Z|X,{\theta }^{(t)}\right)}\right]\\ & \le \log \left[{\mathbb{E}}_{Z\sim p\left(Z|X,{\theta }^{(t)}\right)}\left[\frac{p\left(Z|X,{\theta }^{(t+1)}\right)}{p\left(Z|X,{\theta }^{(t)}\right)}\right]\right]\\ & =\log \left[{\int }_{Z}p\left(Z|X,{\theta }^{(t)}\right)\left[\frac{p\left(Z|X,{\theta }^{(t+1)}\right)}{p\left(Z|X,{\theta }^{(t)}\right)}\right]dZ\right]\\ & =\log {\int }_{Z}p\left(Z|X,{\theta }^{(t+1)}\right)dZ\\ & =0\end{array}$$
综合上面的结果：
$$p(X|{\theta }^t)\le \log p(X|{\theta }^{t+1})$$那么，经过每次的迭代，似然函数在不断的增大。这就证明了我们的更新是有效的，也证明了算法是收敛的。

2 导出公式

机器学习中，所谓的模型实际上就可以看成是一堆的参数。根据极大似然估计的思想，我们要求解的对象是： $${\theta }_{MLE}=logP(X|\theta )$$其中， $X$ 为observed data； $Z$ 为latent data； $(X;Z)$ 为complete data； $\theta$ 为parameter。
那么，EM 公式就被我们描述为：$${\theta }^{t+1}=\underset{\theta }{\mathrm{argmax}}{\int }_Z\log [p(X,Z|\theta )]p(Z|X,{\theta }^t)dZ$$EM 算法可以被我们分解成 E-step 和 M-step 两个部分。

• E-step: $P\left(Z|X,{\theta }^{(t)}\right)⟶{\mathbb{E}}_{Z\sim P\left(Z|X,{\theta }^{(t)}\right)}[\log P(X,Z|\theta )]$

• M-step: ${\theta }^{(t+1)}=\arg {\max }_{\theta }{\mathbb{E}}_{Z\sim P\left(Z|X,{\theta }^{(t)}\right)}[\log P(X,Z|\theta )]$

前面我们已经证明了EM 算法的收敛性了，也就是：
$$\log p(X|{\theta }^t)\le \log p(X|{\theta }^{t+1})$$收敛性告诉了我们算法确实是有效的，我们可以放心的去使用它。而大家会不会觉得这个公式的得来有点懵逼？懵逼就对了，那么下一步，我们的目标就是要推导出EM 算法究竟是怎么来的，给出一个理论的证明。

2.1 从KL Divergence 进行分析

这是个什么东西呢？中文名字叫做“证据下界”。这个名字读起来似乎有一点点奇怪。我们首先看看它是怎么来的。

首先，我们定义一个有关于表示层 $Z$ 的表示层变量 $q(Z)$， $q(Z)$ 可以表示任何一个变量。
$$\begin{array}{rl}\log P(X|\theta )& =\log P(X,Z|\theta )-\log P(Z|X,\theta )\\ & =\log \frac{P(X,Z|\theta )}{Q(Z)}-\log \frac{P(Z|X,\theta )}{Q(Z)}\end{array}$$两边同时对于 $Q(Z)$ 求期望，我们可以得到：
左边：
$$\begin{array}{rl}{\int }_{Z}Q(Z)\log P(X|\theta )dZ& =\log P(X|\theta ){\int }_{Z}Q(Z)dZ\\ & =\log P(X|\theta )\cdot 1\\ & =\log P(X|\theta )\end{array}$$
右边：
$$\underset{ELBO}{\underbrace{{\int }_{Z}Q(Z)\log \frac{P(X,Z|\theta )}{Q(Z)}dZ}}-\underset{KL}{\underbrace{{\int }_{Z}Q(Z)\log \frac{P(Z|X,\theta )}{Q(Z)}dZ}}$$Evidence Lower Bound(ELBO)，是一个下界，所以， $\log P(X|\theta )=ELBO+KL(Q||P)$。其中， $P(Z|X,\theta )$为后验分布(Posterior)。并
且，KL 散度的值一定是大于零的。所以， $ELBO\le logP(X,\theta )$，当且仅当 $P(Z|X,\theta )=Q(Z)$ 时等号成立。
EM 算法的一个想法就是想让 ELBO 不断的增加，从而使 $logP(X|\theta )$不断的变大的一种攀爬的迭代方法。

$logP(X|\theta )$ 是固定的吗？为什么只是让ELBO增大？

那么，我们对下界进行优化，使下界尽可能的变大，就可以使目标函数不断的上升，那么我们可以得到： $$\hat{\theta }=\arg \underset{\theta }{\max }ELBO=\arg \underset{\theta }{\max }\int Q(Z)\log \frac{P(X,Z|\theta )}{Q(Z)}dZ$$因此，实际上也就是用ELBO去逼近 $logP(X,\theta )$，寻找最合适的Q，如果要使得 $ELBO=logP(X,{\theta }^t)$，则需要 $P(Z|X,{\theta }^t)=Q(Z)$，如何求 $Q(Z)$ 见变分推断。
下面使用图来帮助理解EM 算法的一个核心：

在某一时刻 ${\theta }^t$ ,我们可以的得到一个关于 $\theta$ 的函数：
$$\log P\left(X|{\theta }^{(t)}\right)={\int }_{Z}Q(Z)\log \frac{P(X,Z|\theta )}{Q(Z)}dZ-{\int }_{Z}Q(Z)\log \frac{P\left(Z|X,{\theta }^{(t)}\right)}{Q(Z)}dZ$$由于想让 ELBO 更大，此时 $logP(X|{\theta }^t)$ 是一个定值，那么也就是想让 KL 散度的值越小。所以，我们想让 KL 散度的值为零，也就是让 $Q(Z)=P(X|Z,{\theta }^t)$。这一步实际上就是求 $Q(Z)$ 的过程，在图上表示就是上面两幅图，使得 ELBO 与 $logP(X|\theta )$ 相交。这样我们在固定了 ${\theta }^t$ 之后就得到了一个 ELBO 关于 $\theta$ 的函数。然后我们找到这个函数令值最大的 ${\theta }^{t+1}$ 后开始进行下一步迭代。

实际上我们的目的就是在不断的优化 ELBO，使 ELBO 不断的变大，那么我们想要的结果自然也就变大了，这是一个间接优化的方法。整个迭代算法的流程如下图：

那么
$$\begin{array}{rl}\hat{\theta }& =\arg \underset{\theta }{\max }\int Q(Z)\log \frac{P(X,Z|\theta )}{Q(Z)}dZ\\ & =\arg \underset{\theta }{\max }\int P\left(Z|X,{\theta }^{(t)}\right)\log \frac{P(X,Z|\theta )}{P\left(Z|X,{\theta }^{(t)}\right)}dZ\\ & =\arg \underset{\theta }{\max }\int P\left(Z|X,{\theta }^{(t)}\right)[\log P(X,Z|\theta )-\log P\left(Z|X,{\theta }^{(t)}\right)]dZ\end{array}$$
由于 $P\left(Z|X,{\theta }^{(t)}\right)$ 与 $\theta$ 的求解无关（${\theta }^{(t)}$与$\theta$无关）。所以我们可以直接省略掉。那么下一步的 ${\theta }^{t+1}$ 的表达自然也就是：
$$\begin{array}{rl}{\theta }^{(t+1)}& =\arg \underset{\theta }{\max }{\int }_{Z}P\left(Z|X,{\theta }^{(t)}\right)\log P(X,Z|\theta )dZ\\ & =\arg \underset{\theta }{\max }{\mathbb{E}}_{Z\sim P\left(Z|X,{\theta }^{(t)}\right)}[\log P(X,Z|\theta )]\end{array}$$

整个EM算法流程：

2.2 从Jensen Inequality 的角度进行分析

首先，我们介绍一下什么是Jensen Inequality。实际上，进行过一些机器学习理论研究的同学，都应该听说过这个概念。在这里我们做一个简述。首先我们需要保证函数是一个凸函数，下面我们来画一个凸函数：

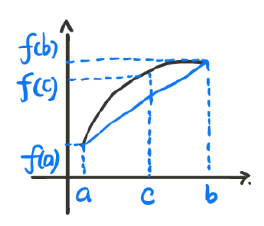
那么对于一个 $t\in [0,1]，c=ta+(1-t)b$，我们都可以得到：
$$f(c)=f[ta+(1-t)b]\ge tf(a)+(1-t)f(b)$$当 t = 1/2 时，我们可以得到： $$f\left(\frac{(a+b)}{2}\right)\ge \frac{1}{2}[f(a)+f(b)]f[E]\ge E[f]$$也就是均值的函数大于函数值的均值

所以，我们可以利用Jensen Inequality 进行推导：
$$\begin{array}{rl}\log P(X|\theta )& =\log {\int }_{z}P(X,Z|\theta )dZ\\ & =\log {\int }_{z}Q(Z)\frac{P(X,Z|\theta )}{Q(Z)}dZ\\ & =\log {\mathbb{E}}_{Z\sim Q(Z)}\left[\frac{P(X,Z|\theta )}{Q(Z)}\right]\\ & \ge {\mathbb{E}}_{Z\sim Q(Z)}\left[\log \frac{P(X,Z|\theta )}{Q(Z)}\right]\end{array}$$
对比上节结果，他就是ELBO，现在来验证 $Q(Z)$ 是不是等于后验 $P(X|Z,{\theta }^t)$ 。

根据Jensen Inequality 的定义，当 $\frac{P(X,Z|\theta )}{Q(Z)}=C$ 时可以取得等号。毫无疑问，当我们取等时，可以达到最大。所以有，
$$\begin{array}{c}\frac{P(X,Z|\theta )}{Q(Z)}=C\\ \\ Q(Z)=\frac{1}{C}P(X,Z|\theta )\\ \\ {\int }_{Z}Q(Z)dZ=\frac{1}{C}{\int }_{Z}P(X,Z|\theta )dZ\\ \\ 1=\frac{1}{C}P(X|\theta )\end{array}$$所以，我们就可以得到： $$Q(Z)=\frac{P(X,Z|\theta )}{P(X|\theta )}=P(Z|X,\theta )$$
所以，大家有没有惊奇的发现，这个 Q(Z) 实际上就是Posterior。当时我们随便引入的一个分布Q(Z)，没想到当它取等的时候就是后验分布。那么像不断去优化这个ELBO，从而使得 $P(X|\theta )$ 的值不断的增加。由于，我们是迭代式的上升这里的 $P(Z|X,{\theta }^t)$，而 ${\theta }^t$ 是上一次迭代得到的，我们可以认为是一个常数。所以，
$$\begin{array}{c}{\mathbb{E}}_{Z\sim Q(Z)}\left[\log \frac{P(X,Z|\theta )}{Q(Z)}\right]={\mathbb{E}}_{Z\sim Q(Z)}\left[\log \frac{P(X,Z|\theta )}{P\left(Z|X,{\theta }^{(t)}\right)}\right]\end{array}$$所以
$$\begin{array}{c}{\theta }^{(t+1)}=\arg {\max }_{\theta }{\mathbb{E}}_{Z\sim Q(Z)}\left[\log \frac{P(X,Z|\theta )}{P\left(Z|X,{\theta }^{(t)}\right)}\right]\end{array}$$​所以，从Jensen Inequality 的角度，我们仍然可以得到 EM 算法的核心表达式。

2.3 小结

在最后，我们再来梳理一下EM 算法的实现思想。我们的目标是想使 $P(X|\theta )$ 似然函数值最大。但是，很不幸，我们直接优化非常的难。所以，我们想到了一个优化下降的方法。对于每一个 ${\theta }^t$ 时，我们可以计算得到下界为： ${\mathbb{E}}_{Z\sim Q(Z)}\left[\log \frac{P(X,Z|\theta )}{P\left(Z|X,{\theta }^{(t)}\right)}\right]$。这个值最大我们就得到了，想要求得的 ${\theta }^{t+1}$。然后，按这个思路，不断的进行迭代。

EM算法的主要工作是去求 $P(X|\theta )$ 中的 ${\theta }^{(t+1)}$。这里实际上是假设使用MLE： ${\theta }_{MLE}=\underset{\theta }{\mathrm{argmax}}\log p(X|\theta )$。但是我们不能直接解，因为不知道 $X$ 服从什么分布，所以我们需要引入一个归纳偏置（假设其服从某个模型），假设存在一个隐变量 $Z$ 能够生成 $X$，因此 $p(X)={\int }_{Z}p(X,Z)dZ$

3 广义EM

本小节中，我们想要介绍三个方便的知识点。

1. 从狭义的EM 算法推广到广义的EM 算法；
2. 狭义的EM 实际上只是广义的EM 的一个特例；
3. 真正的开始介绍EM 算法。

X : O b s e r v e d V a r i a b l e ⟶ X = { x i } i = 1 N X: Observed Variable ⟶ X=\left\{x_{i}\right\}_{i=1}^{N} X:ObservedVariable⟶X={xi​}i=1N​
Z : L a t e n t V a r i a b l e ⟶ Z = { Z i } i = 1 N Z: Latent Variable ⟶ Z=\left\{Z_{i}\right\}_{i=1}^{N} Z:LatentVariable⟶Z={Zi​}i=1N​
$(X,Z)$: Complete Model
$\theta$: Model Parameter
我们希望得到一个参数 $\theta$，可以来推导出 $X$ ，也就是 $P(X|\theta )$ 。而这个参数怎么求得呢？所以，这就是一个learning 的问题了。

3.1 极大似然估计

所以，根据极大似然估计法的思路，我们要求的最优化参数 $\hat{\theta }$ 为：
$$\begin{array}{rl}\hat{\theta }& =\arg \underset{\theta }{\max }P(X|\theta )\\ & =\arg \underset{\theta }{\max }\prod _{i=1}^{N}P\left(x_i|\theta \right)\\ & =\arg \underset{\theta }{\max }\sum _{i=1}^N\log P\left(x_i|\theta \right)\end{array}$$好像，我们这样做就可以解决问题了呀。为什么要多此一举的来引入隐变量 $Z$ 呢？这是因为，我们实际观察的输入空间 $\mathcal{X}$ 的分布 $P(X)$，是非常复杂的。可能什么规律都找不出来，这时我们就想到了一个很好的解决办法。我们引入了一个隐变量 $Z$，这个变量中包含了我们自己的一些归纳总结，引入了内部结构。而 $P(X)={\int }_{Z}P(X,Z)dZ$，实际上就是对 $X$ 进行了分解处理。

3.2 广义的EM 算法

EM 算法是为了解决参数估计问题，也就是learning 问题： $\hat{\theta }=\arg {\max }_{\theta }P(X|\theta )$
但是， $P(X|\theta )$ 可能会非常的复杂。那么，在生成模型的思路中，可以假设一个隐变量Z。有了这个生成模型的假设以后，我们就可以引入一些潜在归纳出的结构进去。通过 $P(X)=\frac{P(X,Z)}{P(Z|X)}$​，就可以把问题具体化了。

这里说明一下，我们习惯用的表达是 $P(X|\theta )$，但是也有的文献中使用 $P(X;\theta )$ 或者 $P_{\theta }(X)$ 。这三种表达方式代表的意义是等价的。

前面我们已经说过了，我们的目标是：
$$\begin{array}{l}\log P(X|\theta )=\underset{L(Q,\theta )}{\underbrace{ELBO}}+KL(Q\Vert P)\ge L(Q,\theta )\\ \{\begin{array}{l}ELBO={\int }_{Z}Q(Z)\log \frac{P(X,Z|\theta )}{Q(Z)}dZ\\ KL(Q\Vert P)={\int }_{Z}Q(Z)\log \frac{Q(Z)}{P(Z|X,\theta )}dZ\end{array}\end{array}l$$但是，问题马上就上来了，那就是 $P(X|\theta )$ 非常有可能求不出来。那么我们怎么来求解这个方程呢？也就是使下界变得更大。

我们之前假定 $Q(Z)=P(Z|X,\theta )$ ，但实际上 $P(Z|X,{\theta }^t)$ 是 intractable 的，如果生成模型较复杂，则无法求出 $P(Z|X,{\theta }^t)$。因此 $Q(Z)$ 无法直接取到 $P(Z)$ ，需要进行优化，逐渐接近 $P(Z)$ 。

首先第一步，我们把 $\theta$ 给固定住。那么， $P(Z|X,\theta )$ 的结果就是一个定值。那么由于 $logP(X|\theta )$ 不变，所以 KL 越小，ELBO 就会越大。由于，Q(Z) 是我们引入的一个中间变量，那么我们的第一步就是得到： $$\hat{Q}(Z)=\arg \underset{Q}{\min }KL(Q\Vert P)=\arg \underset{Q}{\max }L(Q,\theta )$$当 Q 被我们求出来以后，我们就可以将Q 固定了，再来求解 $\theta$： $$\hat{\theta }=\arg \underset{\theta }{\max }L(\hat{q},\theta )$$那么，广义的EM 算法，就可以被我们定义为：
$$\begin{array}{l}E-\text{step}:Q^{(t+1)}=\arg {\max }_{Q}L\left(Q(Z),{\theta }^{(t)}\right)\\ M-\text{step}:{\theta }^{(t+1)}=\arg {\max }_{\theta }L\left(Q(Z{)}^{(t+1)},\theta \right)\\ L(Q,\theta )={\mathbb{E}}_Q[\log P(X,Z)-\log Q]={\mathbb{E}}_Q[\log P(X,Z)]-{\mathbb{E}}_Q[\log Q]\end{array}$$

这里注意 ${\theta }^{(t)}$ 和 $\theta$ 是如何作用的？
为什么在E步要增大ELBO？是要保证KL趋向于0吗（即Q(Z)近似于P(Z)）？控制ELBO和KL中的一个，优化另一个？

看到这里，我估计大家已经可以理解上一小节中，为什么有的 $\theta$ 带(t) 有的不带。因为，首先第一步中是固定 $\theta$ 求Q，这里的 $\theta$ 就是来自于上一次迭代的 ${\theta }^t$。第二次，是将上一步求得的Q 固定，将 $\theta$ 看成参数，来求最优的表达结果的 ${\theta }^{t+1}$。另一个方面，从上面的第三个公式，我们可以看出实际上：
$$ELBO={\mathbb{E}}_{Q(Z)}[\log P(X,Z|\theta )]+H(Q(Z))$$我们对比一下上一节讲到的EM 算法，就会惊奇的发现，ELBO 中最后那个 $H(Q(Z))$ （就是熵， $H(P)=E[-logP]$）竟然不见了。这是为什么呢？其实也很好理解的。因为在M-step 中，我们假定 $Q(Z)$ 已经是固定的了，那么显然 $H[Q(Z)]$ 就是一个定值了，并且与我们的优化目标 $\theta$ 之间并没有任何的关系，所以就被我们给省略掉了。
所以，本小节中引出了广义EM 算法，也说明了原来的EM 算法是广义EM 算法的一种特殊情况。

3.3 坐标上升法

EM 算法的整体描述如下所示： $$\begin{array}{ll}E-\text{step}:& Q^{(t+1)}=\arg {\max }_{Q}L\left(Q(Z),{\theta }^{(t)}\right)\\ M-\text{step}:& {\theta }^{(t+1)}=\arg {\max }_{\theta }L\left(Q(Z{)}^{(t+1)},\theta \right)\end{array}$$这个坐标上升法(SMO) 是个什么东西呢？具体的描述，大家可以去网上找找资料看一看（固定一个，优化另一个，然后固定另一个，优化这个）。两者都是迭代的思路，在这里我们将它和梯度下降法的优化思路放在一起，做一个小小的对比。大家就会发现有什么不一样的地方，

我们发现坐标上升法的优化方向基本是恒定不变的，而梯度下降法的优化方向是随着梯度方向而不断发生改变的。

讲到这里，好像一切都很完美，可以圆满的结束了。但是，很不幸的是，问题马上又来了。因为，现实生活中，并没有那么的容易，一切都没有我们想的那么的简单。实际上，有关 $P(Z|X,\theta )$ 的计算，有可能会非常的复杂。所以，我们将采用变分推断(Variable Inference) 或者马尔可夫蒙特卡罗采样(Markov Chain Monte Carlo) 的方法来求解。结合起来以后就是 VBEM/VEM 和 MCEM 。这里注意一下，Variable Inference 和Variable Bayes 实际上都是一种东西。
当然，虽然 EM 算法看上去好像很厉害的样子。但是，没有一种算法可以一劳永逸的解决所有的问题。它一定存在优点，也一定有无法解决的问题。具体描述，大家可以去网上寻找相关的资料。

版权声明：本文为CSDN博主「AI路上的小白」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/cengjing12/article/details/106480582