论文阅读——SADE:Self-Supervised Aggregation of Diverse Experts for Test-Agnostic Long-Tailed Recognition

论文
代码

任务

Test-Agnostic Long-Tailed Recognition：测试不可知长尾识别，其中训练类分布是长尾的，而测试类分布是不可知的，不一定是一致的。

除了类不平衡的问题外，这项任务还提出了另一个挑战：训练和测试数据之间的类分布变化是未知的。

创新点

（1）一种新的技能多样的专家学习策略，该策略从单一且稳定的长尾数据集中训练多个专家，以分别处理不同的类分布；
（2）一种新颖的测试时专家聚合策略，该策略利用自我监督来聚合所学习的多个专家以处理未知的测试类分布。
图片: 图1 a现有长尾识别方法 b 本文方法

SADE面临的第一个挑战是如何从一个固定的长尾训练数据集中学习多个不同的专家。为了应对这一挑战，我们在这项任务中实证评估了现有的长尾方法，并发现现有方法训练的模型在学习的类分布和训练损失函数之间具有模拟相关性。也就是说，通过各种损失学习的模型熟练地处理具有不同偏度的类分布。例如，用传统的softmax损失训练的模型模拟了长尾训练类分布，而从现有的长尾方法获得的模型擅长于均匀类分布。受这一发现的启发，SADE提出了一种简单但有效的技能多样化专家学习策略，从单个长尾训练分布中生成具有不同分布偏好的专家。在这里，不同的专家分别用不同的专业知识指导的目标函数来处理不同的类分布。因此，学习到的专家比以前的多专家长尾方法更加多样化[49，63]，从而获得更好的集成性能，并总体上模拟了广泛的可能的类分布。

另一个挑战是如何聚集这些技能多样的专家，以便仅基于未标记的测试数据来处理测试不可知的类分布。为了应对这一挑战，我们实证研究了不同专家的性质，并观察到专业知识和预测稳定性之间存在正相关，即更强的专家在其有利类别的样本的不同扰动视图之间具有更高的预测一致性。基于这一发现，我们开发了一种新的自监督策略，即预测稳定性最大化，以仅基于未标记的测试数据自适应地聚集专家。我们从理论上表明，最大化预测稳定性使SADE能够学习聚合权重，该聚合权重使预测的标签分布和真实类别分布之间的互信息最大化。通过这种方式，生成的模型能够模拟未知的测试类分布。

1.1 多专家学习

图2 不同专家指导损失的多专家训练
它包括两个组成部分：
（1）专家共享主干fθ；
（2） 独立专家网络E1、E2和E3。
The forward expert E1：

The uniform expert E2

The backward expert E3

1.2测试时自监督聚合

专家聚集的一个基本原则是，专家在拥有专业知识的情况下应该发挥更大的作用。然而，如何在未知的测试类分布中检测出强大的专家仍然是未知的。我们的关键见解是，即使这些样本受到干扰，强大的专家在预测其熟练班的样本时也应该更加稳定。
为了验证这一假设，我们通过比较专家对样本的两个增广视图的预测之间的余弦相似性来估计专家的预测稳定性。这里，数据视图是通过MoCo v2[5]中的数据扩充技术生成的。从表2中，我们发现专业知识和预测稳定性之间存在正相关，即更强的专家在其有利类别的样本的不同观点之间具有更高的预测相似性。根据这一发现，我们建议探索检测未知测试类别分布的强专家和权重专家的相对预测稳定性。因此，我们开发了一种新的自监督策略，即预测稳定性最大化。
a.Data view generation
sample x ->x1,x2

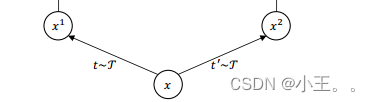
b.Learnable aggregation weight
A learnable aggregation weight w = [w1; w2; w3]
w1 + w2 + w3=1.
c.Objective function
理论上分析预测稳定性最大化策略，以从概念上理解它为什么有效。为此，我们首先将预测和标签的随机变量定义为^Y～p（Y）和Y～pt（Y）。我们得到以下结果：
定理1。预测稳定性S与预测标签分布和测试类分布与之间的互信息I(^Y,Y)成正比例,预测熵H( ^Y)成负比例：

根据定理1，最大化预测稳定性S使得SADE能够学习聚合权重，该聚合权重最大化预测标签分布p（^y）和测试类分布pt（y）之间的互信息，以及最小化预测熵。由于最小化熵有助于提高分类器输出的置信度[12]，因此学习聚合权重来模拟测试类分布pt（y）并提高预测置信度。这一特性直观地解释了为什么我们的方法有潜力在测试时解决测试不可知的长尾识别这一具有挑战性的任务。