[蓝桥杯][2014年第五届真题]斐波那契

题解

题目链接

题解

矩阵快速幂。

数据量太大了，直接模拟过程肯定不行。

---

先看一个结论：S(n) = f(n+2) - 1，其中
S(n) = f(n) + f(n-1) + …… + f(1)，
f(n) = f(n-1) + f(n-2)，
f(1) = f(2) = 1
我是通过打表找到的规律，应该也可以证明出来。（至于你问我为什么会去打表找规律？因为没啥思路了，觉得这么大的数据量，应该不能是遍历求S(n)，所以打表找了一下规律，就发现这个结论了）

这个结论最后再用。

---

遍历求f(n)还是会超时，这里就用到新知识了，矩阵快速幂。

矩阵快速幂讲解

矩阵快速幂的意思就是进行快速幂运算的是矩阵。

快速幂的知识我在这就不讲了，不知道的可以看Here

矩阵快速幂的本质是将递推公式转换为幂次运算，幂次运算又可以通过快速幂算法来快速实现，从而降低了时间复杂度。

---

矩阵快速幂中要进行幂次操作的是矩阵，矩阵的幂次操作就是矩阵进行多次相乘，那我们就先来了解一下矩阵乘法：
A * B = C，其中A、B、C均为矩阵，且A、B、C满足规格要求：A：n×k、B：k×m、C：n×m。
其中C[i][j]为A的第i行与B的第j列对应乘积的和。（线性代数基础）

矩阵乘法代码如下：

struct Matrix { // 我比较喜欢用结构体存一个二维数组表示矩阵，因为传参的时候可以传结构体，而不是一个二维数组
	int m[N][N];
};

Matrix Matrix_mul(Matrix a, Matrix b) {
	Matrix c;
	for(int i = 1;i <= n;i ++) // 矩阵大小为n*n
	for(int j = 1;j <= n;j ++)
	for(int k = 1;k <= n;k ++)
	c.m[i][j] += a.m[i][k] * b.m[k][j];
	return c;
}

快速幂代码如下：

int KSM(int a, int p) { 
	int res = 1;
	while(p) {
		if(p&1) res = res * a;
		a = a * a;
		p>>=1;
	}
	return res;
}

矩阵快速幂代码就是将快速幂中的数值a换成矩阵，函数里面对应的乘法也换成矩阵乘法。

矩阵快速幂代码：

Matrix Matrix_KSM(Matrix a, int p) {
	Matrix res = Matrix(1, 0, 1, 0); // 单位矩阵
	while(p) {
		if(p&1) res = Matrix_mul(res, a);
		a = Matrix_mul(a, a);
		p>>=1;
	}
	return res;
}

为什么矩阵快速幂中的res要初始化为单位矩阵？这与快速幂代码中要将res初始化为1的道理类似，矩阵乘法中任何矩阵乘单位矩阵都是矩阵本身，作用与数值乘法中的1一致，这里的单位矩阵就是起到这样的作用。

---

以上就是矩阵快速幂的基础知识了，下面我们针对本题来说一下如何使用矩阵快速幂解决问题。

我们可以将斐波那契数列的递推公式f(n) = f(n-1) + f(n-2)，转换为矩阵形式（好神奇）：

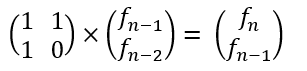
简写成T * A(n-1) = A(n)，T矩阵就是那个2×2的常数矩阵，我们发现数列A就是一个等比数列，公比为常数矩阵T。那我们知道了A(1)之后通过矩阵快速幂不就可以实现计算常数矩阵T的若干次幂了嘛。
举几个例子可以发现，我们要求f(n)，对常数矩阵T进行n次幂的操作后得到的矩阵右上角位置的数即为f(n)的值。
快速幂的时间复杂度是O(logn)，因此我们将时间复杂度从O(n)降至O(logn)。

---

一些其他的递推式变形（感觉蓝桥杯会个Fib的就不错了）：

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

ll n, m, p;

struct Matrix {
	ll m[3][3];
	Matrix() {m[1][1] = m[1][2] = m[2][1] = m[2][2] = 0;}
	Matrix(ll a, ll b, ll c, ll d) {
		m[1][1] = a;
		m[1][2] = b;
		m[2][1] = c;
		m[2][2] = d;
	}
};

ll mul(ll a, ll b, ll mod) {
	ll res = 0;
	while(b) {
		if(b&1) res = (res + a) % mod;
		(a<<=1) %= mod;
		b>>=1;
	}
	return res;
}

Matrix Matrix_mul(Matrix a, Matrix b, ll mod) {
	Matrix res;
	for(int i = 1;i <= 2;i ++)
	for(int j = 1;j <= 2;j ++)
	for(int k = 1;k <= 2;k ++)
	res.m[i][j] = (res.m[i][j] + mul(a.m[i][k], b.m[k][j], mod)) % mod;
	return res;
}

ll Fib(ll n, ll mod) {
	Matrix res = Matrix(1, 0, 1, 0);
	Matrix a = Matrix(1, 1, 1, 0);
	
	while(n) {
		if(n&1) res = Matrix_mul(res, a, mod);
		a = Matrix_mul(a, a, mod);
		n>>=1;
	}
	return res.m[1][2];
}

int main()
{
	cin>>n>>m>>p;
	if(m > n+2) printf("%lld\n", (Fib(n+2, p)  + p - 1) % p); // 如果m>n+2，则S(n) = f(n+2)-1 < f(n+2) < f(m)，那无需对f(m)进行取模操作 
	else {
		ll Fm = Fib(m, LONG_LONG_MAX); // 得到f(m)，因为没法实现边进行矩阵快速幂边取模的操作，因此评测的数据必然能保证将f(m)求出来 
		printf("%lld\n", (Fib(n+2, Fm) + p - 1) % p);  
	}

	return 0;
}

参考

wust_wenhao
顾亦倾