两点间距离、点到直线距离、点到线段距离、线段到线段距离

两点之间的距离

直接运用两点间距离公式 (x2-x1)^ 2+(y2-y1)^ 2开根号

//两点间距离
double getDistancePP(Point a,Point b)
{
   
//这个代码是部分代码,有些逻辑没有展现完全,大家往下看!
    Point c(b.x-a.x,b.y-a.y);//返回一个新的点
    return  c.abs();//取模
}

点到直线距离

通常给出3个点,其中两个点构成一条直线,求另外一个点到直线的距离,我们将点与点的关系转换为向量之间关系进而利用向量知识求出点到直线距离!

点到直线距离,我们可以利用外积的取模公式的几何意义,|axb|=|a|x|b|sinθ=所围成平行四边形面积,先求出向量a✖向量b的模,然后除以平行四边形底边边长|a|,最后用平行四边形面积除以底边边长就是高,也就是点到直线距离!

图解

不明白外积模的几何意义点击下方超链接
外积知识点大全

实现代码

//点到直线距离(利用外积平行四边形)
double getDistancePL(Point a,Point b,Point c)
{
   
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ac(c.x-a.x,c.y-a.y);

    return cross(ab,ac)/ab.abs();//cross函数求两个向量的外积模,abs函数求向量模
}

点到线段距离

点到线段距离有一点复杂,因为线段不像直线那样可以无限延申,线段有端点,这就导致了点到线段距离可以分为3种情况!

第一种:点到线段距离等于点到直线的距离
图示

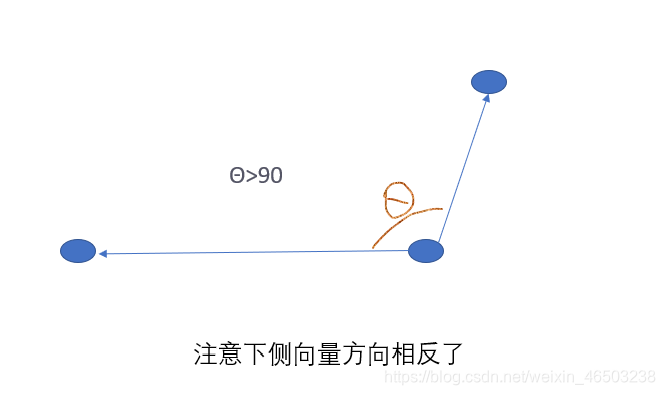
第二种:点到线段距离等于点到左端点的距离
图示

第三种:点到线段等于点到右端点的距离
图示

如何判断θ大小呢?

我们利用内积大小判断 a·b=|a|x|b|cosθ
如果a·b>0则θ在0~90°之间
如果a·b<0则θ在90°~180°之间

实现代码

//点到线段距离
double getDistancePS(Point a,Point b,Point c)
{
   
    //定义4个向量
    Vector ab(b.x-a.x,b.y-a.y);
    Vector ba(a.x-b.x,a.y-b.y);
    Vector ac(c.x-a.x,c.y-a.y);
    Vector bc(c.x-b.x,c.y-b.y);
    //dot函数用于求内积
    if(dot(ab,ac)<0.0) return getDistancePP(a,c);//到左端点距离