（学习笔记）BP神经网络

神经元模型

神经元模型如下：

$\sigma (x$)为激活函数。

BP神经网络结构

$$BP神经网络结构$$
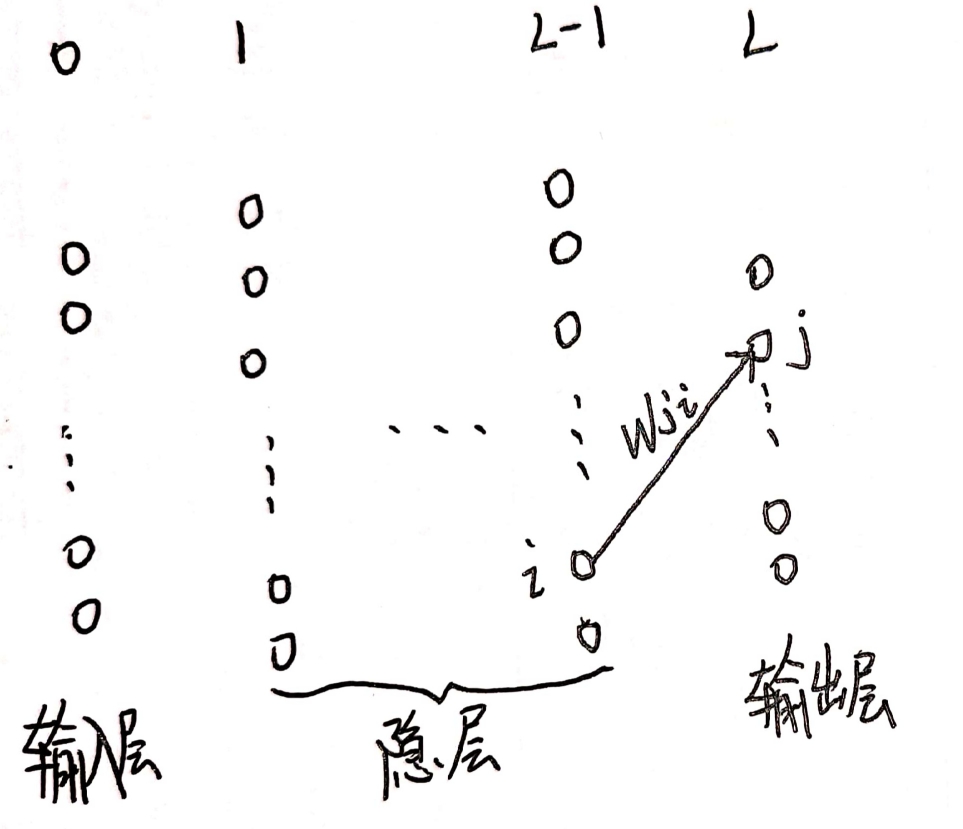
图示BP神经网络相邻两层之间的各神经元相互连接，同一层的神经元不连接。

第一层称为输入层，最后一层称为输出层，中间各层称为隐层。

训练集$D$

训练样本输入$x=[x_1,x_2,...,x_{m^1}]$，样本输出$y=[y_1,y_2,...,y_{m^L}]$

$m^k$为第$k$层神经元的个数。

$w_{ji}^k$为第$k-1$层第$i$个神经元连接第$k$层第$j$个结点的权值。

$y_j^k$为第$k$层第$j$个神经元的输出值，也是第$k+1$层的输入值，$k=0$时，$y^0$即为训练样本输入的$x$。

$b_j^k$为第$k$层第$j$个神经元的阈值。

$z_j^k$为第$k$层第$j$个神经元受到上一层各神经元的输出总和。

$\sigma (x)$为激活函数。

各变量之间的关系：
$$\begin{array}{rl}{z}_j^k=& \sum _i^{m^{k-1}}(w_{ji}^k{y}_i^{k-1}+b_j^k)\\ & \\ y_j^k=& \sigma (z_j^k),k=1,...,L\\ & \\ y^0=& x，x\in D\end{array}$$
对于激活函数，常用的有Sigmoid、ReLU等

$$Sigmoid函数$$

$$ReLU函数$$

BP神经网络算法

训练集$D$

随机初始化网络中的所有权值和阈值
$while$
　$forall(x,y)\in D$
　　计算各层输出值$y^k,k=1,2,...,L-1$
　　计算各层权值和阈值的梯度
　　根据梯度更新权值和阈值
　$end$
$until$到达终止条件　
$BP$算法的目标是最小化训练集上的累积误差
$$\begin{array}{rl}E=& \frac{1}{m}\sum _l^D{J}_l\\ & \\ J_l=& \frac{1}{2}\sum _{j=1}^{m^L}(y_j^L-y_j{)}^2\end{array}$$

误差反向传播推导

BP算法通过反向传播更新权值来进行学习，对于训练样本$(x,y{)}_l$，神经网络输出为$y^L$，误差函数为：
$$\begin{array}{rl}{J}_l=& \frac{1}{2}\sum _{j=1}^{m^L}(y_j^L-y_j{)}^2\end{array}$$
使用梯度下降法更新各层权值和阈值，即沿目标函数的负梯度方向更新权值，因此，神经网络权值修正量为：
$$\begin{array}{r}\Delta w_{ji}^k=-\eta \frac{\partial J}{\partial w_{ji}^k}\\ \\ \Delta b_i^k=-\eta \frac{\partial J}{\partial b_i^k}\\ \\ \eta \in (0,1),称为学习率\end{array}$$
下面进行推导。
对于输出层的神经元的权值：
$$\begin{array}{rl}\frac{\partial J}{\partial w_{ji}^L}=& \frac{\partial J}{\partial z_j^L}\frac{\partial z_j^L}{\partial w_{ji}^L}\end{array}$$
令
$$\begin{array}{rl}{d}_j^L=& \frac{\partial J}{\partial z_j^L}\end{array}$$
则
$$\begin{array}{rl}{d}_j^L=& \frac{\partial J}{\partial y_j^L}\frac{\partial y_j^L}{\partial z_j^L}\\ & \\ =& (y_j^L-y_j){\sigma }^{\prime }(z_j^L)\end{array}$$又
$$\begin{array}{rl}\frac{\partial z_j^L}{\partial w_{ji}^L}=& y_i^{L-1}\end{array}$$
所以
$$\begin{array}{rl}\frac{\partial J_l}{\partial w_{ji}^L}=& \frac{\partial J_l}{\partial z_j^L}\frac{\partial z_j^L}{\partial w_{ji}^L}\\ & \\ =& d_j^L{y}_i^{L-1}\\ & \\ =& \frac{\partial J_l}{\partial y_j^L}\frac{\partial y_j^L}{\partial z_j^L}\frac{\partial z_j^L}{\partial w_{ji}^L}\\ & \\ =& (y_j^L-y){\sigma }^{\prime }(z_j^L)y_i^{L-1}\end{array}$$
对于输出层的神经元的阈值，与权值同理：
$$\begin{array}{rl}\frac{\partial J_l}{\partial b_j^L}=& \frac{\partial J_l}{\partial z_j^L}\frac{\partial z_j^L}{\partial b_j^L}\end{array}$$
由于
$$\begin{array}{rl}\frac{\partial z_j^L}{\partial b_j^L}=& 1\end{array}$$
所以
$$\begin{array}{rl}\frac{\partial J_l}{\partial b_j^L}=& \frac{\partial J_l}{\partial z_j^L}\frac{\partial z_j^L}{\partial b_j^L}\\ & \\ =& d_j^L\\ & \\ =& (y_j^L-y){\sigma }^{\prime }(z_j^L)\end{array}$$
对于隐层的神经元的权值：
以$L-1$层为例:
$$\begin{array}{rl}\frac{\partial J_l}{\partial w_{ji}^{L-1}}=& \frac{\partial J_l}{\partial z_j^{L-1}}\frac{\partial z_j^{L-1}}{\partial w_{ji}^{L-1}}\end{array}$$
同理，
$$\begin{array}{rl}{d}_j^{L-1}=& \frac{\partial J_l}{\partial z_j^{L-1}}\\ & \\ =& \frac{\partial J_l}{\partial y_j^{L-1}}\frac{\partial y_j^{L-1}}{\partial z_j^{L-1}}\\ & \\ =& \frac{\partial J_l}{\partial y_j^{L-1}}{\sigma }^{\prime }(z_j^L)\\ & \\ \frac{\partial z_j^{L-1}}{\partial w_{ji}^{L-1}}=& y_i^{L-2}\end{array}$$
因为
$$\begin{array}{rl}J=& \frac{1}{2}\sum _{j=1}^{m^L}(y_j^L-y_j{)}^2\\ & \\ y_j^L=& \sigma (\sum _i^{m^{L-1}}(w_{ji}^k{y}_i^{L-1}+b_j^L))\end{array}$$
神经网络是全连接，所以
$$\begin{array}{rl}\frac{\partial J_l}{\partial y_j^{L-1}}=& \sum _{i=1}^{m^L}\frac{\partial J}{\partial y_i^L}\frac{\partial y_i^L}{\partial y_j^{L-1}}\\ & \\ =& \sum _{i=1}^{m^L}\frac{\partial J_l}{\partial y_i^L}\frac{\partial y_i^L}{\partial z_i^L}\frac{\partial z_i^L}{\partial y_j^{L-1}}\\ & \\ =& \sum _{i=1}^{m^L}{d}_i^L{w}_{ij}^L\end{array}$$
所以，
$$\begin{array}{rl}\frac{\partial J_l}{\partial w_{ji}^{L-1}}=& \frac{\partial J_l}{\partial z_j^{L-1}}\frac{\partial z_j^{L-1}}{\partial w_{ji}^{L-1}}\\ & \\ =& \frac{\partial J_l}{\partial y_j^{L-1}}\frac{\partial y_j^{L-1}}{\partial z_j^{L-1}}\frac{\partial z_j^{L-1}}{\partial w_{ji}^{L-1}}\\ & \\ =& d_j^{L-1}{y}_i^{L-2}\\ & \\ =& \frac{\partial J}{\partial y_j^{L-1}}{\sigma }^{\prime }(z_j^L)y_i^{L-2}\\ & \\ =& \sum _{i=1}^{m^L}\frac{\partial J_l}{\partial y_i^L}\frac{\partial y_i^L}{\partial z_i^L}\frac{\partial z_i^L}{\partial y_j^{L-1}}{\sigma }^{\prime }(z_j^L)y_i^{L-2}\\ & \\ =& \sum _{i=1}^{m^L}{d}_i^L{w}_{ij}^L{\sigma }^{\prime }(z_j^L)y_i^{L-2}\end{array}$$
对于隐层的神经元的阈值，与权值同理
以L-1层为例：
$$\begin{array}{rl}\frac{\partial J_l}{\partial b_j^{L-1}}=& \frac{\partial J_l}{\partial z_j^{L-1}}\frac{\partial z_j^{L-1}}{\partial b_j^{L-1}}\end{array}$$
$$\begin{array}{r}\frac{\partial z_j^{L-1}}{\partial b_j^{L-1}}=1\end{array}$$
所以
$$\begin{array}{rl}\frac{\partial J_l}{\partial b_j^{L-1}}=& \frac{\partial J_l}{\partial z_j^{L-1}}\frac{\partial z_j^{L-1}}{\partial b_j^{L-1}}\\ & \\ =& d_j^{L-1}\\ =& \sum _{i=1}^{m^L}{d}_i^L{w}_{ij}^L{\sigma }^{\prime }(z_j^L)\end{array}$$
推广到第k层隐层的权值：
$$\begin{array}{rl}\frac{\partial J_l}{\partial w_{ji}^k}=& \frac{\partial J_l}{\partial z_j^k}\frac{\partial z_j^k}{\partial w_{ji}^k}\\ & \\ =& \frac{\partial J_l}{\partial y_j^k}\frac{\partial y_j^k}{\partial z_j^k}\frac{\partial z_j^k}{\partial w_{ji}^k}\\ & \\ =& d_j^k{y}_i^{k-1}\\ & \\ =& \frac{\partial J_l}{\partial y_j^k}{\sigma }^{\prime }(z_j^k)y_i^{k-1}\\ & \\ =& \sum _{i=1}^{m^{k+1}}\frac{\partial J_l}{\partial y_i^{k+1}}\frac{\partial y_i^{k+1}}{\partial z_i^{k+1}}\frac{\partial z_i^{k+1}}{\partial y_j^k}{\sigma }^{\prime }(z_j^k)y_i^{k-1}\\ & \\ =& \sum _{i=1}^{m^{k+1}}{d}_i^{k+1}{w}_{ij}^{k+1}{\sigma }^{\prime }(z_j^k)y_i^{k-1}\end{array}$$
第k层隐层的阈值：
$$\begin{array}{rl}\frac{\partial J_l}{\partial b_j^k}=& \frac{\partial J_l}{\partial z_j^k}\frac{\partial z_j^k}{\partial b_j^k}\\ & \\ =& d_j^k\\ & \\ =& \sum _{i=1}^{m^{k+1}}{d}_i^{k+1}{w}_{ij}^{k+1}{\sigma }^{\prime }(z_j^k)\end{array}$$
根据上面的推导，更新权值和阈值
$$\begin{array}{r}{w}_{ji}^k\leftarrow w_{ji}^k+\Delta w_{ji}^k\\ \\ b_j^k\leftarrow b_j^k+\Delta b_j^k\\ \end{array}$$

BP算法总结

训练集$D$
训练样本输入$x=[x_1,x_2,...,x_{m^1}]$，样本输出$y=[y_1,y_2,...,y_{m^L}]$

各层输出：
$$\begin{array}{rl}{z}_j^k=& \sum _i^{m^{k-1}}(w_{ji}^k{y}_i^{k-1}+b_j^k)\\ & \\ y_j^k=& \sigma (z_j^k)k=1,...,L\\ & \\ y^0=& x，x\in D\end{array}$$
最小化累积误差：
$$\begin{array}{rl}E=& \frac{1}{m}\sum _l^D{J}_l\\ & \\ J_l=& \frac{1}{2}\sum _{j=1}^{m^L}(y_j^L-y_j{)}^2\end{array}$$
权值、阈值更新：
Δ w j i k = − η d j k y i k − 1 Δ b j k = − η d j k d j L = ( y j L − y j ) σ ′ ( z j L ) d j k = ∑ i = 1 m L d i L w i j L σ ′ ( z j L ) , k ∈ { 1 , . . . , L − 1 } \begin{aligned} \Delta{w^k_{ji}}=&-\eta{d^k_jy_i^{k-1}}\\ \\ \Delta{b^k_{j}}=&-\eta{d^k_j}\\ \\ d_j^L=&(y^L_j-y_j)\sigma'(z_j^L)\\ \\ d_j^k=&\sum_{i=1}^{m^{L}}d^L_iw^L_{ij}\sigma'(z_j^L),k\in\{1,...,L-1\} \end{aligned} Δwjik​=Δbjk​=djL​=djk​=​−ηdjk​yik−1​−ηdjk​(yjL​−yj​)σ′(zjL​)i=1∑mL​diL​wijL​σ′(zjL​),k∈{1,...,L−1}​