引言
排序算法第一部分,我们聊了冒泡排序、插入排序、选择排序这三种排序算法,它们的时间复杂度比较高,都是 O(n2),适合小规模数据的排序。今天,我们来看三种时间复杂度为 O(nlogn) 的排序算法,归并排序、快速排序和堆排序。
归并排序和快速排序都用到了“分治”的思想。
一、快速排序(Quick Sort)
快速排序简称为“快排”,思路是:从待排序的数据中,选取一个基准点Pivot,遍历其他元素,将小于基准点的元素放到pivot的左边,将大于基准点的元素放到pivot的右边,将pivot放到中间。经过这一步后,待排序的数据就被分为三个部分:小于pivot的,大于pivot的,中间是pivot。然后,根据同样的思路,递归处理pivot的左右两边的待排数据,直到全部有序。
1.1 完整代码实现:
// 快速排序
int Partion(vector<int>&nums, int start, int end)
{
int povit = nums[start]; // 这里选取第一个元素为基准点pivot
while(start < end){
// 从最后一个元素往前遍历,找到第一个小于等于基准点的元素,注意start < end
while (start < end && nums[end] > povit) end--;
nums[start] = nums[end];
// 从第一个元素往后遍历,找到第一个大于基准点的元素,注意start < end
while (start < end && nums[start] <= povit) start++;
nums[end] = nums[start];
}
// 将基准点放到合适的位置
nums[start] = povit;
// 返回修正后的基准点的下标位置
return start;
}
// @param nums: 待排序原始数据
// @param start:第一个元素的下标
// @param end: 最后一个元素的下标
void QuickSort(vector<int>&nums, int start, int end)
{
if (start < end){
int mid = Partion(nums, start, end);
QuickSort(nums, start, mid-1); // 递归处理pivot左边
QuickSort(nums, mid+1, end); // 递归处理pivot左边
}
return;
}
int main()
{
vector<int> nums = {20, 5, 3, 11, 6, 8, 7, 2};
QuickSort(nums, 0, 7);
cout << "QuickSort: " << endl;
for (int i = 0; i < nums.size(); i++){
cout << nums[i] << " " ;
}
cout << endl;
return 0;
}
运行结果:

小结:快速排序是不稳定的、空间复杂度O(1),时间复杂度为:O(nlogn)的排序算法
1.2 快速排序的应用(获取第K大元素)
void QuickSortGetKth(vector<int>&nums, int start, int end, int k){
if (start < end){
int mid = Partion(nums, start, end);
if (mid == k-1){
cout << "the k is: " << nums[mid] << endl;
return ;
}
else if(mid > k-1)
{
QuickSortGetKth(nums, start, mid-1, k);
}else
{
QuickSortGetKth(nums, mid+1, end, k);
}
}
return;
}
二、归并排序(Merge Sort)
归并排序的思路:将待排序的数据,从中间分为前后两个部分,分别对前后两个部分进行排序,再将排好序的前后两部分进行合并,最终完全有序。
分治一般用递归来实现。递归的要素就是:找到递推公式,找到终止条件,再将递推公式翻译为代码。
递推公式:
MergeSort(start, end) = Merge(MergeSort(start, mid), MergeSort(mid+1, end));
终止条件:
start >= end 不再继续分解
完整代码实现
// 归并排序
void Merge(vector<int>& nums, int start, int mid, int end) // 合并函数
{
int i = start, j = mid+1, k = 0;
vector<int> tmp(end-start+1); // 开辟临时空间
while (i <= mid && j <= end)
{
if (nums[i] <= nums[j])
{
tmp[k++] = nums[i++];
}
else{
tmp[k++] = nums[j++];
}
}
while (i <= mid){
tmp[k++] = nums[i++];
}
while (j <= end){
tmp[k++] = nums[j++];
}
for (int i = 0; i < end-start+1; i++){
nums[i+start] = tmp[i];
}
return;
}
void MergeSort(vector<int>& nums, int start, int end)
{
if (start >= end) return;
int mid = start + ((end - start) >> 1);
MergeSort(nums, start, mid); // 继续分解前半部分,直到不满足分解条件
MergeSort(nums, mid+1, end);
Merge(nums, start, mid, end);
return ;
}
int main()
{
vector<int> nums = {20, 5, 3, 11, 6, 8, 7, 2};
MergeSort(nums, 0, 7);
cout << "MergeSort: " << endl;
for (int i = 0; i < nums.size(); i++){
cout << nums[i] << " " ;
}
cout << endl;
return 0;
}
运行结果:

代码运行分析:
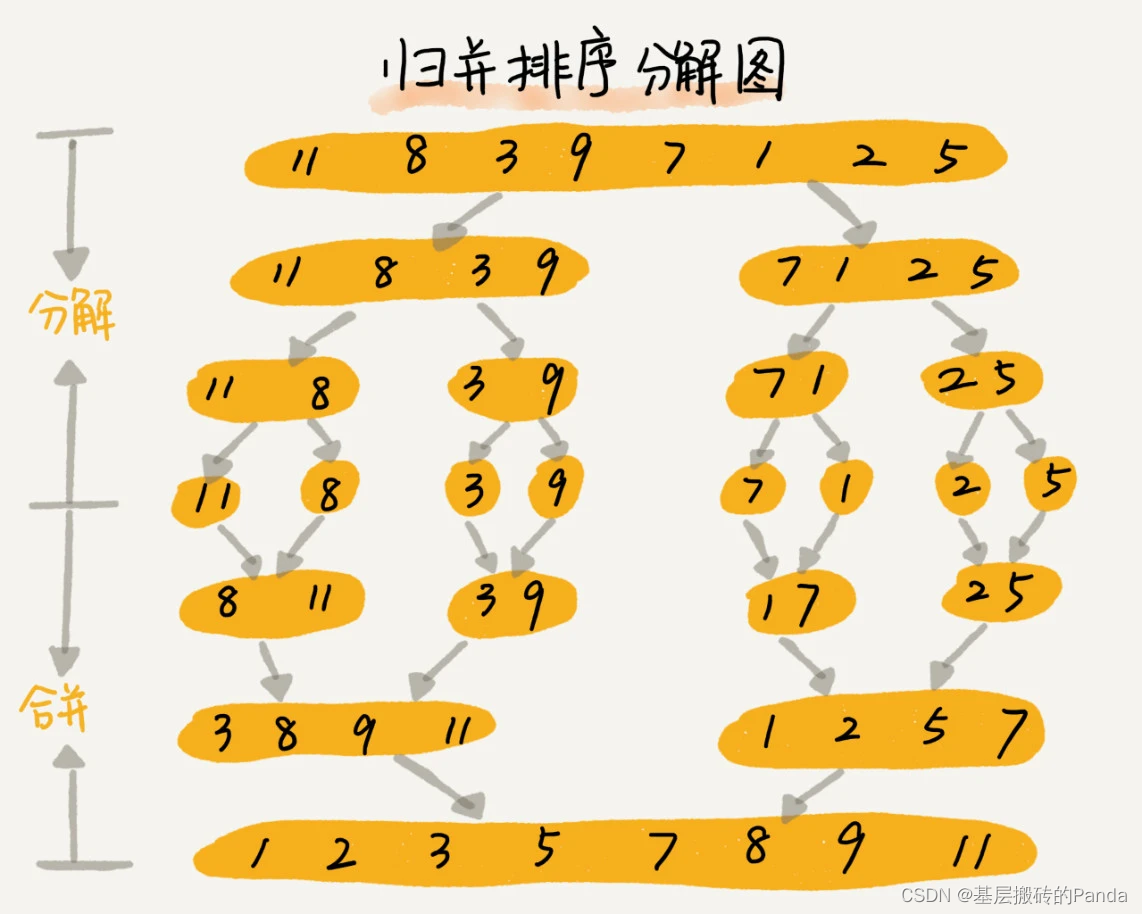
假设待排序的数据:nums = {11, 8, 3, 9, 7, 1, 2, 5},则:MergeSort(nums,0, 7); start = 0, end=7,mid = 3;
第一次分解:
前半部分:11, 8, 3, 9 ;此时 s = 0,e = 3,mid = 1; 执行 MergeSort(nums,0, 3)
后半部分:7, 1, 2, 5;此时 s = 4,e = 7,mid = 5; 执行 MergeSort(nums,4, 7) ;
前半部分11, 8, 3, 9 继续分解(递归进行)
第二次分解:
子前半部分:11, 8;此时 s = 0, e = 1,mid = 0; 执行 MergeSort(nums,0, 0) 和 MergeSort(nums,1, 1) 。注意
MergeSort(nums,0,0)和 MergeSort(nums,1,1)因为,if (start >= end) return; 本次递归结束,进入到Merge(nums,0,0,1)合并函数。注意,此时,子前半部分只有两个元素:11,8,开辟2个元素大小的临时空间。比较元素大小,按顺序放入临时空间,也就是[8,11] 。然后,返回到上一次递归MergeSort(nums, 0, 3);
子后半部分:3, 9;此时 s = 2, e = 3,mid = 2; 执行 MergeSort(nums,2, 2) 和 MergeSort(nums,3, 3) 。注意
MergeSort(nums,2,2)和 MergeSort(nums,3,3)因为,if (start >= end) return; 本次递归结束,进入到Merge(nums,2,3,3)合并函数。注意,此时,子后半部分只有两个元素:3,9,开辟2个元素大小的临时空间。比较元素大小,按顺序放入临时空间,也就是[3,9] 。然后,也返回到上一次递归MergeSort(nums, 0, 3);
进入到合并函数Merge(nums, 0, 1, 3); 此时,开辟3-0+1 = 4个元素大小的临时空间。比较元素大小,按顺序放入临时空间,也就是[3,8,9,11] 。
后半部分7, 1, 2, 5 继续分解(递归进行),有兴趣的小伙伴可以自己分析以下,思路同上。
最终,前后两部分合并为一个有序数组:[1,2,3,5,7,8,9,11]
小结:归并排序是稳定的,空间复杂度O(n),时间复杂度为O(nlogn)。
三、堆排序
3.1 堆的基础知识
堆一般指的是二叉堆,顾名思义,二叉堆是完全二叉树或者近似完全二叉树。
性质
- 是一棵完全二叉树
- 每个节点小于其子节点的值称为“小顶堆”,反之称为“大顶堆”
存储
一般用数组来表示堆,下标为i的节点的父节点下标为:(i-1)/2,其左右子几点下标分别为:(2i+1)和(2i+2)。
堆的操作(以大顶堆为例)
堆中定义了以下几种操作:
- 创建堆(BuildHeap)
- 堆调整(AdjustHeap):将堆的末端子节点作调整,使得子节点永远小于等于父节点
3.2 堆排序分析(图文结合,仔细阅读,一定能掌握堆排序)
实现堆排序思路:
- 如何由一个无序序列建成一个堆?
- 如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
假设: nums = {20, 5, 3, 11, 6, 8, 7, 2}, size = 8

创建堆:从第一个非叶子节点(下标为 size/2-1 = 3 的位置)开始调整,直到根节点(下标为0的位置)。
思考:为什么要从第一个非叶子节点开始调整呢?因为默认叶子节点满足大顶堆的性质。
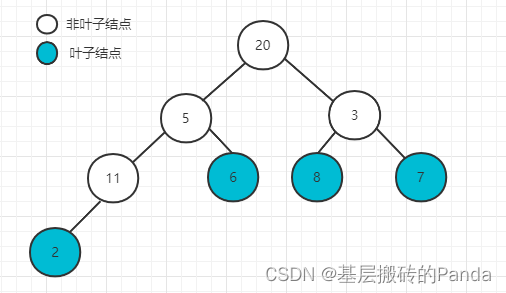
下标为 i = 3 的节点,因为只有左孩子,满足大顶堆性质,且maxIdx == i,本次调整结束如下图:
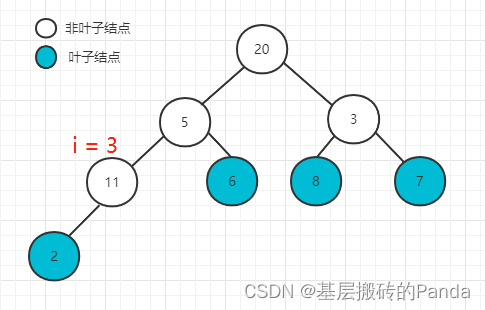
下标为 i = 2 的节点, 因为左孩子为8,右孩子为7,maxIdx = 5,因为maxIdx != 2,交换并继续调整maxIdx。因为maxIdx的节点不满足调整条件,本次调整结束,如下:
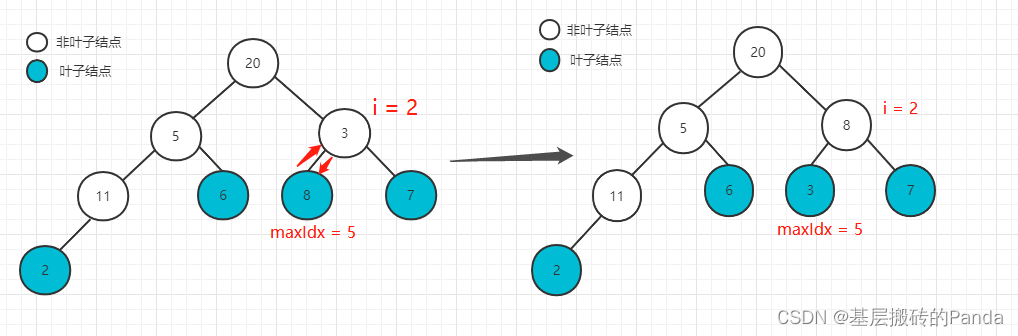
下标为 i = 1的节点,左孩子为11,右孩子为6,最大值为11,则与最大值11交换,最大值的maxIdx = 3,继续进入AdjustHeap函数,此时,maxIdx位置的元素为5,左右节点已经满足大顶堆的性质,本次调整结束,如下:
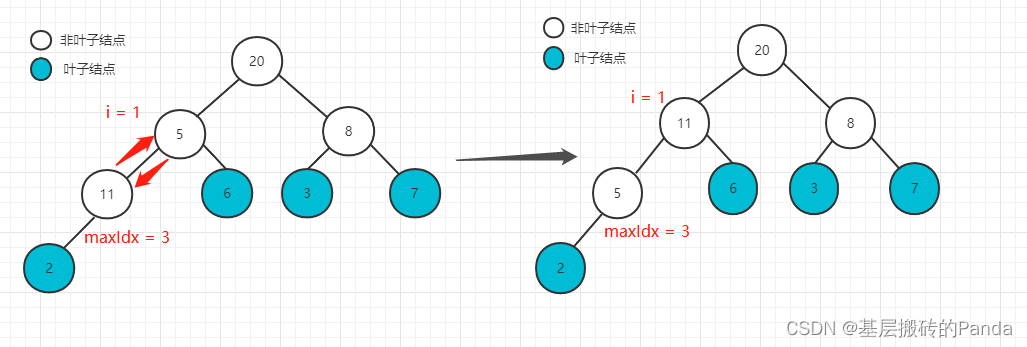
下标为 i = 0的节点,已满足大顶堆的性质,本次调整结束,如下:
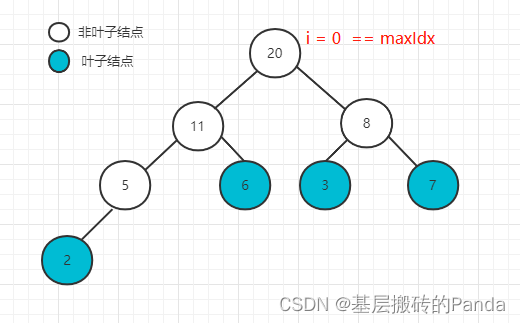
到这一步BuildHeap函数执行结束。此时,堆顶元素就是本次排序中最大的元素。
后面的思路就是,把堆顶元素与数组的最后一个元素进行交换,然后继续调整第一个元素,使之成为次大值,循环往复,直到最后一个元素。注意,每确定一个当前的最大值后,AdjustHeap(nums, maxIdx, size)函数的size需要减1。
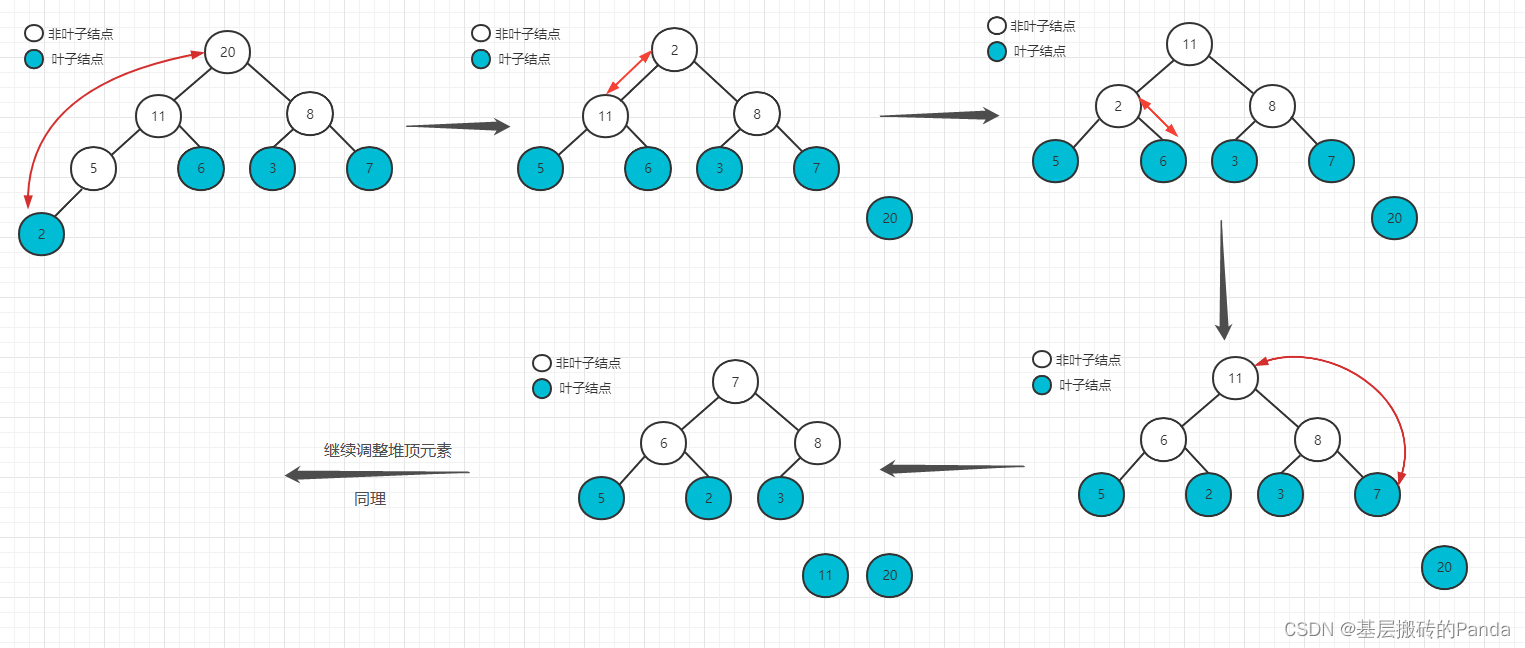
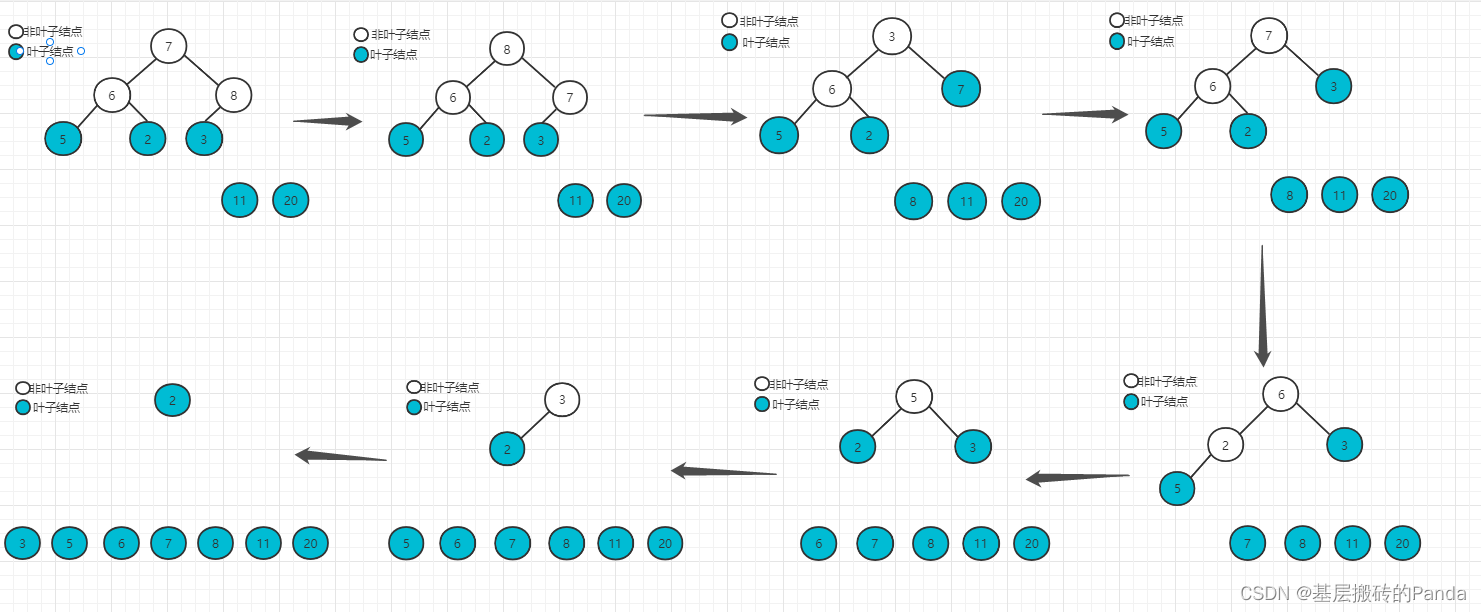
3.3 堆排序完整代码实现
// 堆排序
void AdjustHeap(vector<int>&nums, int i, int size){
int maxIdx = i;
int lChild = 2*i+1, rChild = 2*i+2;
if (lChild < size && nums[lChild] > nums[maxIdx]){
maxIdx = lChild;
}
if (rChild < size && nums[rChild] > nums[maxIdx]){
maxIdx = rChild;
}
if (maxIdx != i){
swap(nums[maxIdx], nums[i]);
AdjustHeap(nums, maxIdx, size);
}
return;
}
void BuildHeap(vector<int>&nums, int size)
{
for (int i = size/2-1; i >= 0; i--){
AdjustHeap(nums, i, size);
}
return;
}
void HeapSort(vector<int>&nums)
{
int size = nums.size();
BuildHeap(nums, size);
for (int i = size-1; i >= 0; i--){
swap(nums[0], nums[i]); // 将堆顶元素与“最后一个元素交换”,继续调整
AdjustHeap(nums, 0, i); // 注意这里i的变化
}
return;
}
int main()
{
vector<int> nums = {20, 5, 3, 11, 6, 8, 7, 2};
HeapSort(nums);
cout << "Heap Sort: " << endl;
for (int i = 0; i < size; i++){
cout << nums[i] << " " ;
}
cout << endl;
return 0;
}
运行结果:

小结:堆排序是不稳定的,空间复杂度O(1),时间复杂度为O(nlogn)。
四、总结
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 Merge合并函数。同理,理解快排的重点也是理解递推公式,还有 partition() 分区函数。
归并排序算法的时间复杂度在任何情况下都比较稳定,缺点是归并排序不是原地排序算法,空间复杂度比较高O(n)。正因为此,它也没有快排应用广泛。快速排序算法虽然最坏情况下的时间复杂度是 O(n2),但是平均情况下时间复杂度都是 O(nlogn)。快速排序时间复杂度退化到 O(n2) 的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
堆排序需要好好揣摩创建堆、调整堆的思路,一定能熟练掌握。






















 1818
1818











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








