编译原理——程序语言的语法描述（笔记）

yjx23332

已于 2022-03-24 21:56:22 修改

阅读量1.8k

点赞数 2

分类专栏：编译原理（笔记）文章标签：编译原理

于 2022-03-10 22:52:18 首次发布

本文链接：https://blog.csdn.net/weixin_46949627/article/details/123387681

版权

编译原理（笔记）专栏收录该内容

7 篇文章

订阅专栏

本文深入探讨了形式语言的理论基础，包括有穷字母表、字与字符串的概念，以及闭包和正规闭包的定义。上下文无关文法作为文法的一种，通过四元组形式进行描述，并通过产生式来定义语言结构。此外，文章还讨论了文法的直接推出和星号推出，以及最左推导和最右推导，强调了语法树在理解文法结构中的作用。最后，提到了文法的二义性和无二义性问题，以及乔姆斯基层次的文法分类。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

连接、闭包、正规闭包

考虑一个有穷字母表∑ 字符集
其中每一个元素称为一个字符
∑ 上的字(字符串)是指由∑中的字符所构成的一个有穷序列
不包含任何字符的序列称为空字，记为ε
用∑*表示∑上的所有字的全体，包含空字ε

例如 : 设 ∑ ={a ， b} ，则 ∑* ={ε,a,b,aa,ab,ba,bb,aaa,...}

∑* 的子集 U 和 V 的连接（积）定义为 UV ＝ $\{\alpha \beta| \alpha \epsilon U$ $\&\beta \epsilon V\}$

设： U ＝ { a, aa } V ＝ { b, bb }

那么： UV= { ab, abb, aab, aabb}

∑* 的子集 U 和 V 的连接（积）定义为UV ＝ { $\alpha \beta| \alpha \epsilon U$ & $\beta \epsilon V$ }

V 自身的 n 次积记为 $V^n$ =V V…V （选n个V内的字拼接，字可相同可不相同）

规定 $V^0$ ={ε}

令 V*= $V^0\cup V^1\cup V^2\cup V^3$ ...

称 V* 是 V 的闭包

记 $V^+$ ＝VV*，称 V+ 是 V 的正规闭包（正则闭包）

大多数情况，闭包与正规闭包没有不同。

但，当V没有空字时，V的闭包有空字，V的正规闭包没空字。

上下文无关文法

文法：描述语言的语法结构的形式规则

一个上下文无关文法 G 是一个四元式 G=( $V_T$ ， $V_N$ ，S，P) ，其中：

$V_T$ ：终结符集合 ( Terminal，非空，最小有意义单位，无法再被分解定义。以英语为例，单词的种类就是终结符)

$V_N$ ：非终结符集合 ( Not Terminal，非空,语法单位。如英语中的语法单位) 且 $V_T$ $\cap$ $V_N$ = $\phi$

S：文法的开始符号（文法所定义的最大/最重要的语法单位。如英文中的句子）， $S\epsilon V_N$

P：产生式集合 ( 有限 ) ，每个产生式形式为 $P\rightarrow \alpha ,P\epsilon V_N,\alpha \epsilon (V_T\cup V_N)^*$ ，开始符 S 至少必须在某个产生式的左部出现一次（ $\alpha$ 是由终结符与非终结符组成的任意串）

$\rightarrow$ ：定义符。

例

定义只含+，*的算术表达式的文法G：

G=< {i，+，*，(，)}，{E}，E，P>，

$V_T$ ：i，+，*，(，)

$V_N$ ：E

S：E

P：P

其中，P由下列产生式组成：

组成	翻译
E $\rightarrow$ i	E(表达式)可以由单独的一个 i 构成
E $\rightarrow$ E+E	E(表达式)可以由一个‘+’连接两个E（表达式）构成
E $\rightarrow$ E*E	E(表达式)可以由一个‘*’连接两个E（表达式）构成
E $\rightarrow$ (E)	E(表达式)可以由一个‘(’')'包裹一个E（表达式）

巴科斯范式 (BNF)

“ $\rightarrow$ ” 也可以用“ ::=" 表示，这种表示称为巴科斯范式 (BNF)

几点约定

$\begin{equation}P \rightarrow \alpha_1\\ P \rightarrow \alpha_2\\ P \rightarrow \alpha_3\\ ...\\ P \rightarrow \alpha_n \end{equation}$ 可缩写为 $P\rightarrow \alpha_1|\alpha_2|...|\alpha_3$ ，（‘|’读做'或'）

一般大写字母开头符号位非终结符；小写字母、运算符、分界符开始的符号为终结符

表示一个文法时，通常只给出开始符号和产生式。比如：G(E) ： E $\rightarrow$ i | E+E | E*E | (E)

直接推出

直接推出：把一个串中间的一个定义符号，替换为它的定义式。

定义：称 $\alpha A \beta$ 直接推出 $\alpha \gamma \beta$ ，即 $\alpha A\beta \Rightarrow \alpha \gamma \beta$

当且仅当 $A\rightarrow \gamma$ 是一个产生式，且 $\alpha ,\beta\epsilon \left ( V_T\cup V_N \right )^*$ 。

（将一个由终结符与非终结符组成的任意串，将串中的一个终结符的一次出现替换为它的一个定义式，得到一个新的串。旧串与新串的关系就是直接推出）

如果 $\alpha_1 \Rightarrow \alpha_2 \Rightarrow ...\Rightarrow \alpha_n$ ,则我们称这个序列式从 $\alpha_1$ 到 $\alpha_n$ 的一个推导。若存在一个从 $\alpha_1$ 到 $\alpha_n$ 的推导，则称 $\alpha_1$ 可以推导出 $\alpha_n$ 。

例子：

因此，对文法G(E):E $\rightarrow$ i | E+E | E*E | (E)

E $\Rightarrow$ (E) $\Rightarrow$ (E+E) $\Rightarrow$ (i+E) $\Rightarrow$ (i+i)

结论：(i+i)是合法的串。

加号推出

用 $\alpha_1\overset{+}{\Rightarrow} \alpha_n$ 表示：从 $\alpha_1$ 出发经过一步或若干步可以推出 $\alpha_n$ 。

星号推出

用 $\alpha_1\overset{*}{\Rightarrow}\alpha _n$ 表示：从 $\alpha_1$ 出发，经过0步或者若干步，可以推出 $\alpha_n$ 。

定义：

假定G是一个文法，S是它的开始符号，如果 $S\overset{*}{\Rightarrow}\alpha$ ，则称 $\alpha$ 是一个句型。

仅含终结符号的句型是一个句子。

文法G所产生的句子的全体是一个语言，将它记为L(G)。 $L(G) = \{\alpha |S\Rightarrow \alpha ,\alpha \epsilon V_T^*\}$

下图中，He gave me a book 为句子。

（换言之，句型（ $\alpha$ ）包含句子（ $V_T$ ）以及句子成分（ $V_N$ ），或者说 $\alpha\epsilon $V_N\cup V_T$^*$ )

对于语言而言，显然不能有句子成分，因此 $L(G) = \{\alpha |S\Rightarrow \alpha ,\alpha \epsilon V_T^*\}$ 。

例：

证明(i*i+i) 是文法 G(E)：E $\rightarrow$ i | E+E | E*E | (E) 的一个句子。

（G(E)中E就是指代一个产生式）

证明：

E $\Rightarrow$ (E)

$\Rightarrow$ (E+E)

$\Rightarrow$ (E*E+E)

$\Rightarrow$ (i*E+E)

$\Rightarrow$ (i*i+E)

$\Rightarrow$ (i*i+i)

例：给出产生语言为 { $a^nb^n$ |n $\geq$ 1} 的文法

(递归思想）

G(S) ：

S $\rightarrow$ aSb（n个ab的组合S替换，使得满足上式，可作为句型）

S $\rightarrow$ ab（n=1,即递归中基础部分,满足上式，可作为基础的语句）

例：给出产生语言为 { $a^mb^n$ |1 $\leq$ n $\leq$ m $\leq$ 2n} 的文法

G(S) ：

S $\rightarrow$ ab | aab（m=1,n=1或者m=2,n=1，满足上式，作为基础的语句）

S $\rightarrow$ aSb | aaSb（m=1,n=1加上任意个m=1,n=1或者m=2,n=1，满足上式，m=2,n=1同理可知。因而可作为句型）

从一个句型到另一个句型的推导往往不唯一

$E+E\Rightarrow i+E\Rightarrow i+i$

$E+E\Rightarrow E+i \Rightarrow i+i$

最左推导：任何一步 $\alpha \Rightarrow \beta$ 都是对 $\alpha$ 中的最左非终结符进行替换

最右推导：任何一步 $\alpha \Rightarrow \beta$ 都是对 $\alpha$ 中的最右非终结符进行替换

语法树与二义性

用一张图表示一个句型的推导 , 称为语法树

G(E) ： E $\rightarrow$ i | E+E | E*E | (E)

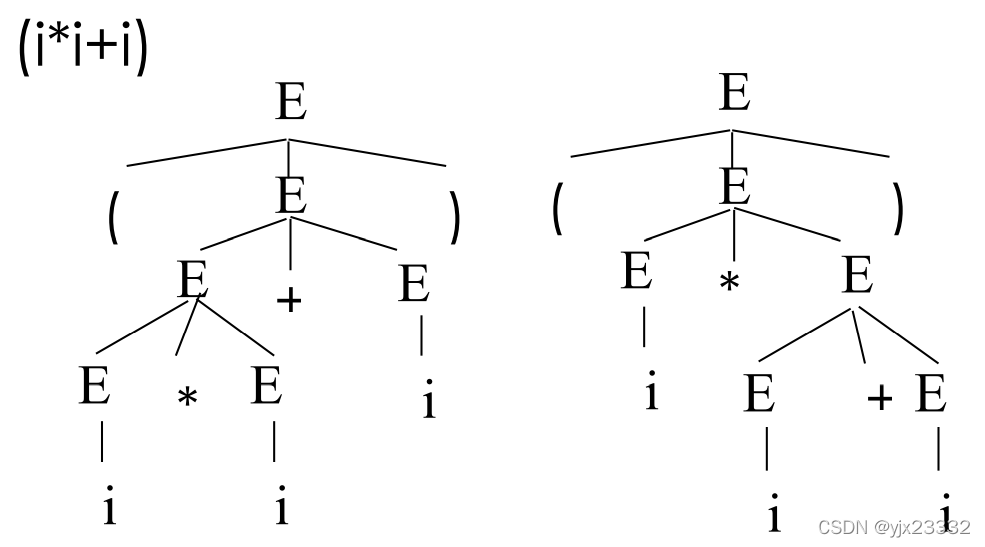
定义：如果一个文法存在某个句子对应两棵不同的语法树，则说这个文法是二义的

语言与文法的二义性

一个语言是二义性的，如果对它不存在无二义性的文法。

但是，可能存在G和G’，一个为二义性的，一个为无二义性的。但 L(G)=L(G’)

二义性问题是不可判定问题，即不存在一个算法，它能在有限步骤内，确切地判定一个文法是否是二义的。但我们可以找到一组无二义文法的充分条件。

无二义性文法

$G(E) :$

$E\rightarrow T | E+T$

$T\rightarrow F | T*F$

$F \rightarrow (E) | i$

1. 不含 P $\rightarrow$ P 形式的产生式

2. 每个非终结符P必须有用处

乔姆斯基形式语言体系

乔姆斯基于 1956 年建立形式语言体系，他把文法分成四种类型： 0，1，2，3型

与上下文无关文法一样，它们都由四部分组成，但对产生式的限制有所不同

从0型开始不断增加限制条件（类似数据库的范式）。

0型（短语文法，图灵机）

产生式形如： $\alpha \rightarrow \beta$

其中： $\alpha \epsilon (V_T \cup V_N )^*$ 且至少含有一个非终结符；

则 $\beta \epsilon (V_T \cup V_N )^*$

1型（上下文有关文法，线性界限自动机）

产生式形如： $\alpha \rightarrow \beta$

其中： $|\alpha |\leq |\beta |$ ，仅 $S\rightarrow \varepsilon$ 例外

2型（上下文无关文法，非确定下推自动机）

产生式形如： $A\rightarrow\beta$

其中： $A\epsilon V_N; \beta \epsilon (V__T\cup V_N)^*$

3型（正规文法，有限自动机）

右线性文法

产生式形如： $A\rightarrow \alpha B$ 或 $A\rightarrow \alpha$

其中： $\alpha \epsilon V_T^*;A,B\epsilon V_N$

左线性文法

产生式形如： $A\rightarrow B\alpha$ 或 $A\rightarrow \alpha$

其中： $\alpha \epsilon V_T^*;A,B\epsilon V_N$