day 14 SHAP可视化-CSDN博客

本文链接：https://blog.csdn.net/weixin_47130140/article/details/147749846

一、原理——合作博弈论

SHAP（SHapley Additive exPlanations）是一种用于解释机器学习模型预测结果的方法，它基于合作博弈论中的 Shapley 值概念。Shapley 值最初用于解决合作博弈中的利益分配问题。假设有 n 个参与者共同合作完成一项任务并获得一定收益，Shapley 值能公平地分配这个总收益给每个参与者，它考虑了每个参与者在所有可能的合作组合中的边际贡献。

在机器学习中，特征的边际贡献指的是某个特征在模型中对预测结果所带来的额外价值或影响。它衡量了在已有其他特征的基础上，单独添加该特征后模型性能的提升程度。

例如：甲、乙、丙、丁四个工人一起打工，甲和乙完成了价值100元的工件，甲、乙、丙完成了价值120元的工件，乙、丙、丁完成了价值150元的工件，甲、丁完成了价值90元的工件，那么该如何公平、合理地分配这四个人的工钱呢？

这里每个工人获得的工钱反映了他在不同组合中对最终价值产出的独特贡献。这里通过对比不同工人组合完成工件价值的差异，来确定每个工人的贡献。比如从 “甲和乙完成价值 100 元工件” 到 “甲、乙、丙完成价值 120 元工件”，差值 20 元体现了丙在这个组合变化中的贡献，即丙的工钱。

二、shapley值计算思路

特征组合枚举：对于一个有 n 个特征的模型，需要考虑所有可能的特征子集组合。例如，当有 3 个特征 A、B、C 时，特征子集包括空集 {}，单特征集 {A}、{B}、{C}，双特征集 {A, B}、{A, C}、{B, C}，以及包含所有特征的集合 {A, B, C}。总共有 $2^n$ 种组合。

边际贡献计算：对于每个特征子集 S ，计算包含该特征 i （ i ∉ S ）和不包含该特征 i （即子集 S ）时模型预测值的差异，这个差异就是特征 i 在特征子集 S 下的边际贡献。

平均边际贡献（shap值）：对特征 i 在所有可能的特征子集组合下的边际贡献进行加权平均，权重是该子集组合出现的概率，得到的结果就是该特征的 SHAP 值。正值表示该特征倾向于使模型预测值增加，负值表示倾向于使模型预测值减少。

三、shap的关键特性

基准值代表了在没有考虑任何特定样本特征时，模型基于整个训练数据集的平均预测输出。例如，在一个预测房价的模型中，如果对训练数据集中所有房屋的价格求平均，得到的这个平均价格就是基准值。它为解释模型对特定样本的预测提供了一个参考点。

加性特性解释：SHAP 的加性特性表明，对于任何一个样本的预测，模型预测值可以分解为基准值与每个特征的 SHAP 值之和。也就是说，每个特征对模型预测值的贡献是独立可加的。

假设有一个预测客户是否会购买产品（0 ：不购买，1 ：购买）的模型，基准值为 0.3（即平均来看，在不考虑任何客户特征时，模型预测客户购买产品的概率是 0.3）。对于某个特定客户，特征 1（比如客户年龄）的 SHAP 值为 0.1，特征 2（比如客户收入）的 SHAP 值为 0.2，特征 3（比如客户购买历史）的 SHAP 值为 0.05。根据 SHAP 的加性特性，该客户的模型预测值就是基准值加上各个特征的 SHAP 值，即 0.3+0.1+0.2+0.05=0.65 ，这意味着考虑了该客户的年龄、收入和购买历史等特征后，模型预测该客户购买产品的概率为 0.65。

四、`shap_values` 数组

SHAP 旨在深入剖析模型对单个样本做出预测的内在原因。对于每个样本的预测，需要明确每个特征对预测值的作用方向（是使预测值升高还是降低）以及作用程度（升高或降低了多少）。SHAP 值直观地反映了特征对样本预测值的 “推力”，SHAP 值的绝对值越大，说明该特征对预测值的影响越显著。

回归问题：

模型输出特点：回归模型的输出是一个连续的数值，例如预测房价、温度等。

计算逻辑：对于数据集中的每个样本（共n_samples个），都要计算每个特征（共n_features个）对该样本预测值的 SHAP 值。

数组结构：shap_values生成的是一个numpy数组，它的形状为 (n_samples, n_features)。例如，shap_values[10, 3] 表示第 10 个样本的第 3 个特征对该样本预测值的贡献。

即：shap_values.shape = (n_samples, n_features)

分类问题：

模型输出特点：分类模型通常为每个类别输出一个分数或概率，例如在判断一封邮件是垃圾邮件还是正常邮件时，模型会给出邮件属于垃圾邮件和正常邮件的概率。

计算逻辑：SHAP 需要分别解释模型是如何得出每个类别的分数的。所以对于每个样本，要针对每个类别分别计算每个特征的 SHAP 值。

数组结构：常见的组织方式是返回一个列表，列表长度等于类别数。列表的第 k 个元素是一个 (n_samples, n_features) 的numpy数组，表示所有样本的所有特征对预测类别k的贡献。

即：shap_values.shape =(n_samples, n_features, n_classes)

例如二分类问题中，shap_values[0][10, 3] 表示第 10 个样本的第 3 个特征对该样本被预测为第 0 类的贡献；shap_values[1][10, 3] 则表示第 10 个样本的第 3 个特征对该样本被预测为第 1 类的贡献。

总结：

SHAP 通过计算 Shapley 值，将模型预测分解到每个特征上，这种分解针对每个样本、每个特征以及分类问题中的每个类别都要进行，从而形成了特定结构的shap_values数组。通过这个数组，我们能够清晰地了解模型预测背后每个特征的作用，为模型解释提供了有力的工具。

五、代码实例

import shap
import matplotlib.pyplot as plt

# 初始化 SHAP 解释器，他会分析模型结构，为后续计算shap值做准备
explainer = shap.TreeExplainer(rf_model)

# 计算 SHAP 值（测试集），这个计算耗时
shap_values = explainer.shap_values(X_test)

# 生成所有特征对每个样本预测结果的影响程度
shap_values

array表示不同类别，每行表示单个样本，每列表示单个特征，值表示特征对样本预测结果的影响程度，正值表示正向影响，负值表示负向影响。

注意！！！分类问题返回的是列表，列表没有shape属性，所以会报错：

将列表转化为数组，形状为(num_classes, n_samples, n_features)
shap_array = np.array(shap_values)
#根据索引对维度进行转置，变成 (n_samples, n_features, num_classes)
shap_array_aligned = np.transpose(shap_array, axes=(1, 2, 0))
shap_array_aligned.shape
# 输出：（1500,31,2）

print("shap_array_aligned shape:", shap_array_aligned.shape)
print("shap_array_aligned[0] shape:", shap_array_aligned[0].shape)
print("shap_array_aligned[:, :, 0] shape:", shap_array_aligned[:, :, 0].shape)
print("X_test shape:", X_test.shape)
# 输出：
shap_array_aligned shape: (1500, 31, 2)
shap_array_aligned[0] shape: (31, 2)
shap_array_aligned[:, :, 0] shape: (1500, 31)
X_test shape: (1500, 31)

shap_array_aligned[:, :, 0] ：

第一个 : 表示选取第一个维度（样本维度）上的所有元素。

第二个 : 表示选取第二个维度（特征维度）上的所有元素。

0 表示选取第三个维度（类别维度）上索引为 0 的元素。

shap_array_aligned 的形状是 (n_samples, n_features, num_classes)，经过这个切片操作后，会得到一个新的二维数组，其形状为 (n_samples, n_features)。这个新数组包含了所有样本的所有特征对于类别索引为 0 的 SHAP 值。

在处理多维数组切片时，start:stop:step 这种格式中 step 用于指定步长，即每隔多少个元素取一个。但当只写一个数字，如这里的 0，它就被当作索引，用来精确获取指定位置的元素。如果想要在第三个维度上使用步长，格式会变为 shap_array_aligned[:, :, ::2]，这表示在第三个维度上，从开头开始，每隔一个元素（步长为 2）进行选取。

上面这些输出有点玄学，不同电脑可能输出不同，中间的2个谁和x_test的尺寸一样就选谁

特征重要性条形图

print("--- 1. SHAP 特征重要性条形图 ---")
#  show=False表示不立即显示图形,这样可继续用plt自定义修改图形
shap.summary_plot(shap_array_aligned[:, :, 0], X_test, plot_type="bar",show=False)  
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()

特征重要性蜂巢图

print("--- 2. SHAP 特征重要性蜂巢图 ---")
shap.summary_plot(shap_array_aligned[:, :, 0], X_test,plot_type="violin",show=False,max_display=10) 
# max_display=10 表示只显示对预测结果影响最大的前 10 个特征，默认为20.
plt.title("SHAP Feature Importance (Violin Plot)")
plt.show()

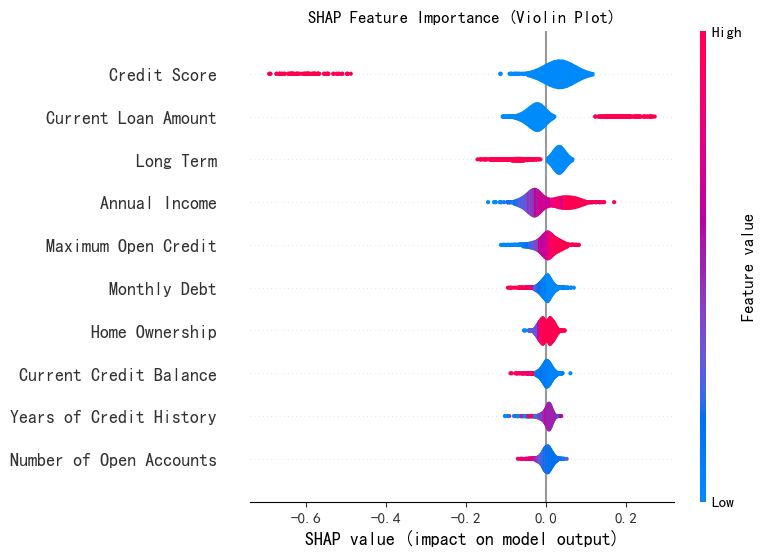注意！！！小提琴图的横轴表示单个样本中特征的shap值，和条形图横轴表示特征在所有样本的特征平均值。