数据结构之二叉平衡树

躺平的小懒猫

于 2023-09-16 12:37:06 发布

阅读量190

点赞数

分类专栏：数据结构与算法文章标签：数据结构

本文链接：https://blog.csdn.net/weixin_47225948/article/details/132917157

版权

数据结构之二叉平衡树

一、C 二叉平衡树源码实现及详解
二、C++ 二叉平衡树源码实现及详解

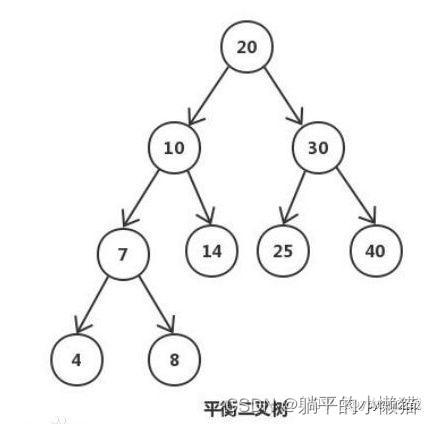
二叉平衡树是一种自平衡二叉搜索树，具有以下特点：

每个节点的左子树和右子树的高度差最多为1；
每个节点的左子树和右子树也都是一棵二叉平衡树。

实现原理：

插入操作：向二叉平衡树中插入一个元素时，先按照二叉搜索树的规则找到插入位置，然后从插入位置开始向上追溯，检查每个节点的平衡因子是否超过1。若超过1，则需要通过旋转操作进行平衡处理。具体来说，可以分为四种情况：

LL型：在节点的左子树的左子树上插入节点导致不平衡，需要进行右旋操作；
RR型：在节点的右子树的右子树上插入节点导致不平衡，需要进行左旋操作；
LR型：在节点的左子树的右子树上插入节点导致不平衡，需要进行先左旋再右旋操作；
RL型：在节点的右子树的左子树上插入节点导致不平衡，需要进行先右旋再左旋操作。

删除操作：从二叉平衡树中删除一个元素时，先按照二叉搜索树的规则找到要删除的节点，然后进行删除操作。删除后，从删除位置开始向上追溯，检查每个节点的平衡因子是否超过1。若超过1，则需要通过旋转操作进行平衡处理，具体处理方式与插入操作相同。

通过插入和删除操作的平衡处理，可以使二叉平衡树保持平衡，从而提高了搜索、插入和删除的效率。

在这里插入图片描述

一、C 二叉平衡树源码实现及详解

二叉平衡树是一种自平衡的二叉搜索树，它的每个节点都满足以下性质：

它的左子树和右子树的高度之差不超过1；
它的左子树和右子树都是一棵二叉平衡树。

二叉平衡树的平衡操作包括左旋和右旋。左旋是指将一个节点的右子树作为新的子树，同时该节点成为新子树的左子树；右旋是指将一个节点的左子树作为新的子树，同时该节点成为新子树的右子树。

以下是 C 实现的二叉平衡树代码，其中包括节点的插入、删除和打印操作：

#include <stdio.h>
#include <stdlib.h>

struct TreeNode {
   
    int val;
    int height;
    struct TreeNode* left;
    struct TreeNode* right;
};

int max(int a, int b) {
   
    return a > b ? a : b;
}

int height(struct TreeNode* node) {
   
    return node == NULL ? -1 : node->height;
}

int getBalance(struct TreeNode* node) {
   
    return node == NULL ? 0 : height(node->left) - height(node->right);
}

struct TreeNode* createNode(int val) {
   
    struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    node->val = val;
    node->height = 0;
    node->left = NULL;
    node->right = NULL;
    return node;
}

struct TreeNode* leftRotate(struct TreeNode* node) {
   
    struct TreeNode* newRoot = node->right;
    node->right = newRoot->left;
    newRoot->left = node;
    node->height = max(height(node->left), height(node->right)) + 1;
    newRoot->height = max(height(newRoot->left), height(newRoot->right)) +