欧几里得算法与扩展欧几里得算法——公钥密码的数学基础

欧几里得算法

欧几里得算法也叫辗转相除法，用于计算两个正整数的最大公约数（gcd）

计算

我们先来求16和6的最大公约数吧！

其实我们口算就能算出来最大公约数是2。下面是我们一般手算的做法：

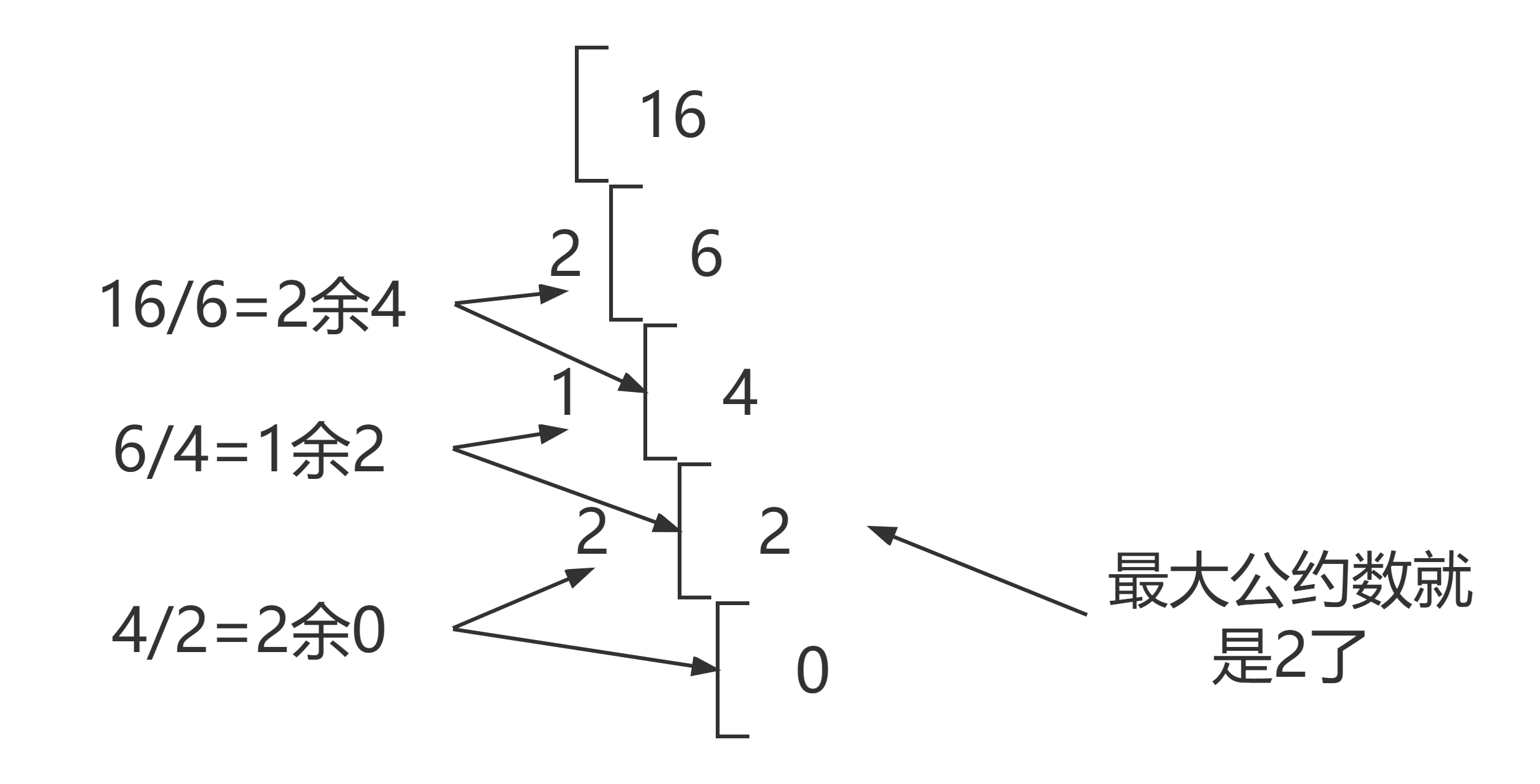
使用数学计算可以表示为：

16 / 6 = 2 余 4
6 / 4 = 1 余 2
4 / 2 = 0，因此最大公约数为2

上面的步骤可以总结如下：

假设两个正整数a和b（a>=b）

1、r = a mod b

2、如果r = 0，则b为最大公约数。否则，将b赋值给a，r赋值给b，然后返回第一步执行

代码

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

证明 *

可以通过归纳法来证明。假设有两个正整数a和b，其中a > b。则根据欧几里得算法的定义，我们可以将a表示成：

a = bq + r

其中q为商数，r为余数，且0 <= r < b。如果r=0，显然b即为最大公约数；否则，我们可以继续使用较小的数b和余数r进行相同的操作，直到余数为0为止。

我们需要证明gcd(a, b) = gcd(b, r)是成立的，因此我们需要证明以下两个命题：

• 命题1：如果x能同时整除a和b，则x也必然能同时整除b和r。
• 命题2：如果y能同时整除b和r，则y也必然能同时整除a和b。

对于命题1，我们可以将a和b表示为x的倍数，即a=k1x，b=k2x，则有：

r = a - bq = k1x - k2qx = (k1 - k2q)x

由于x能同时整除a和b，因此x也必然能整除r。

对于命题2，我们可以将b和r表示为y的倍数，即b=k3y，r=k4y，则有：

a = bq + r = k3yq + k4y = (k3q + k4)y

由于y能同时整除b和r，因此y也必然能整除a，证毕。

因此，根据归纳法原理和以上两个命题，欧几里得算法是正确的，它总能找到两个正整数的最大公约数。

扩展欧几里得算法

扩展欧几里得算法（Extended Euclidean Algorithm）是求解两个正整数a和b的最大公约数gcd(a, b)以及一对整数x和y，使得ax + by = gcd(a, b)。它可以用于解决模线性方程、计算乘法逆元等问题。

其原理如下：

假设有两个正整数a和b（a >= b），并令r为a除以b所得的余数。我们需要求解形如ax + by = gcd(a, b)的一对整数x和y，其中x和y的值可以是负数。

根据辗转相除法，我们可以得到：

• 如果b等于0，则gcd(a, b)等于a，此时x等于1，y等于0。

• 如果b不等于0，则递归调用扩展欧几里得算法来求解(b, r)的解，并将结果命名为(x1, y1)。然后，我们可以通过以下公式计算(a, b)的解：

  x = y1

  y = x1 - [a / b] * y1【注：[a / b]表示a被b整除】

由于(a, b) = (b, r)，因此(x1, y1)是(b, r)的解。因此，上述公式给出了(a, b)的解。

计算

我们以16和6举例，进行扩展欧几里得算法的计算演示。

首先根据欧几里得算法，我们得到：

16 = 6 * 2 + 4
6 = 4 * 1 + 2
4 = 2 * 2 + 0

因此最大公约数是2。那么在此过程中，我们希望通过ax + by = gcd(a, b)，求出每一对(x, y)。那我们知道根据欧几里得算法，最后递归出口是gcd(2, 0)，从而得到最大公约数是2，因此gcd(2, 0) = 2x + 0y = 2，那么我们可以得到其中一个解就是(1, 0)，故：

gcd(2, 0) = 2 * x + 0 * y => (1, 0)
带入公式x = y1, y = x1 - [a / b] * y1：
(0, 1) =>  4 * x + 2 * y = gcd(4, 2)
(1, -1) => 6 * x + 4 * y = gcd(6, 4)
(-1, 3) => 16 * x + 6 * y = gcd(16, 6)

即存在(x, y) = (-1, 3)，使得16 * x + 6 * y = gcd(16, 6)

代码

def egcd(a, b):
    if b == 0:
        return 1, 0
    else:
        x2, y2 = egcd(b, a % b)
        x1, y1 = y2, x2 - a // b * y2
    return x1, y1

证明 *

扩展欧几里得算法就是在欧几里得算法的基础上求出一条线性方程ax + by = gcd(a, b)

因此，在递归的过程中，我们要记录每一步中a和b的系数x和y，使得满足以下等式：

a * x + b * y = gcd(a, b)

当b = 0时，a即为最大公约数，此时ax + 0y = a，可求出解(x, y) = (1, 0)，也是作为递归的出口

当b != 0时，有：

a * x + b * y = gcd(a, b)
b * x1 + (a mod b) * y1 = gcd(b, a mod b)

由于a mod b = a - [a / b] * b（其中[a / b]表示a整除b），代入得：

b * x1 + (a - [a / b] * b) * y1 = gcd(b, a mod b)

由欧几里得算法可知gcd(b, a mod b) = gcd(a, b)，代入：

b * x1 + (a - [a / b] * b) * y1 = gcd(a, b)
即a * y1 + b * (x1 - [a / b] * y1) = gcd(a, b)

解得x = y1, y = x1 - [a / b] * y1，也就是最终可以根据该等式求得a * x + b * y = gcd(a, b)，即存在x、y使得等式成立，证毕

求乘法逆元

由扩展欧几里得算法，有：

a * x + b * y = gcd(a, b)

当a和b互质时，有gcd(a, b) = 1，即：

a * x + b * y = 1

将等式mod b，得：

a * x + b * y mod b = 1 mod b

因为b * y被b整除，所以有：

a * x = 1 mod b

即当a和b互质时，存在逆元x使得a * x = 1 mod b

举例

3和5互质，求3相对5的乘法逆元。我们使用上面的egcd函数，得到结果为(2, -1)，即3 * 2 + 5 * (-1) = 1，此时 3 * 2 = 1 mod 5，即2就是3相对5的乘法逆元