目录
李群李代数基础
三维旋转矩阵构成了特殊正交群
SO
(3)
,而变换矩阵构成了
特殊欧氏群
SE
(3)
:
群
群(
Group
)是
一种集合
加上
一种运算
的代数结构。把集合记作
A
,运算记作
·, 那么群可以记作
G
= (
A,
·
)
。群要求这个运算满足以下几个条件:
1.
封闭性
: 
2.
结合律
:

3.
幺元
: 
4.
逆
:

李群是指具有连续(光滑)性质的群。而
SO(
n) 和
SE(
n),它们在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动,所以它们都是李群。
李代数的引出
考虑任意旋转矩阵  满足:
满足:
在等式两边对时间求导,得到:
整理:
可以找到一个三维向量  ,与之对应。于是有:
,与之对应。于是有:
等式两边右乘
 :
:
每对旋转矩阵求一次导数,只需左乘一个矩阵  即可。在
即可。在
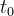 附近,设
附近,设 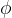 保持为常数
保持为常数
 ,则有:
,则有:
由初始值  ,解微分方程:
,解微分方程:
李代数的定义
每个李群都有与之对应的李代数。李代数描述了李群的局部性质。通用的李代数的定义如下:
李代数由一个集合  ,一个数域
,一个数域  和一个二元运算
[
,
]
组成。如果它们满足以下几条
和一个二元运算
[
,
]
组成。如果它们满足以下几条
性质,称 ( ,
,  , [
,
])
为一个李代数,记作
g
。
, [
,
])
为一个李代数,记作
g
。
1.
封闭性 :
![\forall X,Y\in\mathbb{V},[X,Y]\in\mathbb{V}](https://latex.csdn.net/eq?%5Cforall%20X%2CY%5Cin%5Cmathbb%7BV%7D%2C%5BX%2CY%5D%5Cin%5Cmathbb%7BV%7D)
2.
双线性 :  ,有
,有 ![[a\boldsymbol{X}+b\boldsymbol{Y},\boldsymbol{Z}]=a[\boldsymbol{X},\boldsymbol{Z}]+b[\boldsymbol{Y},\boldsymbol{Z}]](https://latex.csdn.net/eq?%5Ba%5Cboldsymbol%7BX%7D+b%5Cboldsymbol%7BY%7D%2C%5Cboldsymbol%7BZ%7D%5D%3Da%5B%5Cboldsymbol%7BX%7D%2C%5Cboldsymbol%7BZ%7D%5D+b%5B%5Cboldsymbol%7BY%7D%2C%5Cboldsymbol%7BZ%7D%5D) ,
,
3.
自反性:![\forall X\in\mathbb{V},[X,X]=0](https://latex.csdn.net/eq?%5Cforall%20X%5Cin%5Cmathbb%7BV%7D%2C%5BX%2CX%5D%3D0)
4.
雅可比等价: ![\forall X,Y,Z\in\mathbb{V},[X,[Y,Z]]+[Z,[Y,X]]+[Y,[Z,X]]=0](https://latex.csdn.net/eq?%5Cforall%20X%2CY%2CZ%5Cin%5Cmathbb%7BV%7D%2C%5BX%2C%5BY%2CZ%5D%5D+%5BZ%2C%5BY%2CX%5D%5D+%5BY%2C%5BZ%2CX%5D%5D%3D0)
其中二元运算被称为
李括号
。
李代数 
每个 都可以生成一个反对称矩阵:
在此定义下,两个向量
 的李括号为:
的李括号为:
则
李群SO(3)对应的李代数
 :
:
它与
SO
(3)
的关系由指数映射给定:
李代数
与 相似,
位于
空间中:
前三维为平移,记作  ;后三维为 旋转,记作
;后三维为 旋转,记作 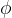 。
在这里同样使用
。
在这里同样使用  符号将六维向量扩展成为四维矩阵,但不再表示反对称:
符号将六维向量扩展成为四维矩阵,但不再表示反对称:
李括号为:
指数与对数映射
SO(3) 上的指数映射
对  中任意一元素
中任意一元素 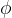 ,定义它的指数映射:
,定义它的指数映射:
由于 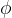 是三维向量,我们可以定义它的模长和它的方向,分别记作
是三维向量,我们可以定义它的模长和它的方向,分别记作 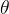 和
和  ,于是有
,于是有  。这里
。这里  是一个长度为 1 的方向向量。首先,对于
是一个长度为 1 的方向向量。首先,对于  ,有以下两条性质:
,有以下两条性质:
以及
利用这两个性质,可以把指数映射写成:
得到了一个似曾相识的式子:
SE(3) 上的指数映射
其中:
可以看到,平移部分经过指数映射之后,发生了一次以 为系数矩阵的线性变换。
李群李代数转换关系如下图:

李代数求导与扰动模型
使用李代数的一大动机是为了进行优化。
BCH 公式与近似形式
李群乘积和李代数加法并不等价。
两个李代数指数映射乘积的完整形式,由 Baker-Campbell-Hausdorff
公式(
BCH 公式)
给出。由于它完整的形式较复杂,展开式的前几项:
其中
[]
为李括号。
BCH 公式告诉我们,当处理两个矩阵指数之积时,它们会产生一些由 李括号组成的余项。特别地,考虑
SO
(3) 上的李代数  ,当
,当
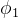 或
或
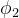 为小量时,小量二次以上的项都可以被忽略掉。此时,BCH 拥有线性近似表达:
为小量时,小量二次以上的项都可以被忽略掉。此时,BCH 拥有线性近似表达:
左乘
BCH
近似雅可比  事实上就是从
事实上就是从
 对数映射中的雅可比矩阵:
对数映射中的雅可比矩阵:
它的逆为:
而右乘雅可比仅需要对自变量取负号即可:
某个旋转  (
对应的李代数为
(
对应的李代数为 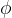 )
左乘一个微小旋转
)
左乘一个微小旋转  (对应的李代数为
(对应的李代数为  )得到的
)得到的 对应的李代数为:
对应的李代数为:
在李代数上进行加法,让一个 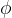 加上
加上  :
:
对于
SE
(3),亦有类似的BCH
近似公式:
李代数求导
使用李代数解决求导 问题的思路分为两种:
1.
用李代数表示姿态,然后对根据李代数加法来对李代数求导。
2.
对李群
左乘
或
右乘
微小扰动,然后对该扰动求导,称为左扰动和右扰动模型。
对一个空间点 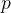 进行了旋转,得到了
进行了旋转,得到了  ,旋转之后点的坐标对旋转的导数可表示为:
,旋转之后点的坐标对旋转的导数可表示为:
由于
SO
(3)
没有加法,所以该导数无法按照导数的定义进行计算。
李代数加法求导
转而计算:
按照导数的定义,有:
第二行的近似为 BCH 线性近似,第三行为泰勒展开舍去高阶项后近似,第四行至第 五行将反对称符号看作叉积,交换之后变号。旋转后的点相对于李代数的导数:
于这里仍然含有形式比较复杂的  。
。
扰动模型求导
旋转 进行一次扰动
,左乘后的李代数对
求导,即:






















 387
387

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








