《视觉SLAM十四讲》公式笔记（ch03三维空间刚体运动)

三丫Nono

于 2024-05-29 21:37:45 发布

阅读量896

点赞数 20

分类专栏： SLAM 文章标签：笔记

本文链接：https://blog.csdn.net/weixin_47445781/article/details/139279365

版权

SLAM 专栏收录该内容

3 篇文章 0 订阅

订阅专栏

点和向量，坐标系

只有当我们指定这个三维空间中的某个坐标系时，才可以谈论该向量在此坐标系下的坐标，也就是找到若干个实数对应这个向量。如果我们确定一个坐标系，也就是一个线性空间的基

$(e_1,e_2,e_3)$ ，那就可以谈论向量 $\boldsymbol{a}$ 在这组基下的坐标 $[\mathrm{a}_{1},\mathrm{a}_{2},\mathrm{a}_{3}]^{\mathrm{T}}$ 了：

$\boldsymbol{a}=[\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3]\left[\begin{array}{c}a_1\\\\a_2\\\\a_3\end{array}\right]=a_1\boldsymbol{e}_1+a_2\boldsymbol{e}_2+a_3\boldsymbol{e}_3.$

内积可以描述向量间的投影关系。对于 $a,b\in\mathbb{R}^3$ ，内积可以写成：

$\boldsymbol{a}\cdot\boldsymbol{b}=\boldsymbol{a}^T\boldsymbol{b}=\sum_{i=1}^3a_ib_i=\left|\boldsymbol{a}\right|\left|\boldsymbol{b}\right|\cos\left\langle\boldsymbol{a},\boldsymbol{b}\right\rangle$

外积可以写成：

$\small\left.\boldsymbol{a}\times\boldsymbol{b}=\left[\begin{array}{ccc}\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k}\\\\a_1&a_2&a_3\\\\b_1&b_2&b_3\end{array}\right.\right]=\left[\begin{array}{ccc}a_2b_3-a_3b_2\\\\a_3b_1-a_1b_3\\\\a_1b_2-a_2b_1\end{array}\right]=\left[\begin{array}{ccc}0&-a_3&a_2\\\\a_3&0&-a_1\\\\-a_2&a_1&0\end{array}\right]\boldsymbol{b}\triangleq\boldsymbol{a}^\wedge\boldsymbol{b}$

其中， $\boldsymbol{a}^{\wedge}$ 表示 $\boldsymbol{a}$ 的反对称矩阵。

坐标系间的欧氏变换

相机运动是一个刚体运动，它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。

旋转矩阵 $\boldsymbol{R}$ 的推导:

设某个单位正交基 $(e_1,e_2,e_3)$ 经过一次旋转，变成了 $(\boldsymbol{e}_1^{'},\boldsymbol{e}_2^{'},\boldsymbol{e}_3^{'})$ 。那么，对于同一个向量 $\boldsymbol{a}$ （注意该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为 $[a_1,a_2,a_3]^T$ 和 $[a_1^{'},a_2^{'},a_3^{'}]^T$ 。根据坐标的定义，有：

$\left.[\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3]\left[\begin{array}{c}a_1\\\\a_2\\\\a_3\end{array}\right.\right]=\left[\boldsymbol{e}_1^{'},\boldsymbol{e}_2^{'},\boldsymbol{e}_3^{'}\right]\left[\begin{array}{c}a_1^{'}\\\\a_2^{'}\\\\a_3^{'}\end{array}\right]$

对上面等式左右同时左乘 $[e_1^T,e_2^T,e_3^T]^T$ ，那么左边的系数变成了单位矩阵：

$\left.\left[\begin{array}{c}a_1\\\\a_2\\\\a_3\end{array}\right.\right]=\left[\begin{array}{ccc}e_1^Te_1^{'}&e_1^Te_2^{'}&e_1^Te_3^{'}\\e_2^Te_1^{'}&e_2^Te_2^{'}&e_2^Te_3^{'}\\e_3^Te_1^{'}&e_3^Te_2^{'}&e_3^Te_3^{'}\end{array}\right]\left[\begin{array}{c}a_1^{'}\\a_2^{'}\\a_3^{'}\end{array}\right]\triangleq\boldsymbol{R}\boldsymbol{a}^{'}$

矩阵 $\boldsymbol{R}$ 描述了旋转本身。因此它又称为旋转矩阵。

旋转矩阵的性质

事实上，它是一个行列式为 1 的正交矩阵 。反之，行列式为 1 的正交矩阵也可以是一个旋转矩阵。所以，可以把旋转矩阵的集合定义如下：

$SO(n)=\{\boldsymbol{R}\in\mathbb{R}^{n\times n}|\boldsymbol{R}\boldsymbol{R}^T=\boldsymbol{I},\det(\boldsymbol{R})=1\}$

旋转矩阵可以描述相机的旋转。由于旋转矩阵为正交阵， 它的逆（即转置）描述了一个相反的旋转。按照上面的定义方式，有：

$a^{{^{\prime}}}=R^{-1}a=R^{T}a$

欧氏空间的坐标变换

考虑世界坐标系中的向量 $\boldsymbol{a}$ ，经过一次旋转（用 $\boldsymbol{R}$ 描述）和一次平移 $\boldsymbol{t}$ 后，得到了 $a^{{^{\prime}}}$ ，那么把旋转和平移合到一起，有：

$a^{^{\prime}}=Ra+t$

变换矩阵与齐次坐标

假设进行了两次变换：

$b=R_1a+t_1,\quad c=R_2b+t_2$

则：

$c=R_2\left(R_1a+t_1\right)+t_2$

因此，要引入齐次坐标和变换矩阵重写式：

$\left[\begin{array}{c}a^{{^{\prime}}}\\\\1\end{array}\right]=\left[\begin{array}{cc}R&t\\\\\mathbf{0}^{T}&1\end{array}\right]\left[\begin{array}{c}a\\\\1\end{array}\right]\triangleq\boldsymbol{T}\left[\begin{array}{c}a\\\\1\end{array}\right]$

对于这个四维向量，我们可以把旋转和平移写在一个矩阵里面，使得整个关系变成了线性关系。该式中，矩阵 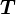$\boldsymbol{T}$ 称为 变换矩阵（Transform Matrix）。我们暂时用 $\tilde{\boldsymbol{a}}$ 表示 $\boldsymbol{a}$ 的齐次坐标。

依靠齐次坐标和变换矩阵，两次变换的累加就可以有很好的形式：

$\widetilde{b}=\boldsymbol{T}_1\widetilde{\boldsymbol{a}},\widetilde{\boldsymbol{c}}=\boldsymbol{T}_2\widetilde{\boldsymbol{b}}\quad\Rightarrow\widetilde{\boldsymbol{c}}=\boldsymbol{T}_2\boldsymbol{T}_1\widetilde{\boldsymbol{a}}$

在不引起歧义的情况下，以后我们就直接把它写成 $\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a}$ 的样子，默认其中是齐次坐标了。

变换矩阵的性质

它具有比较特别的结构：左上角为旋转矩阵，右侧为平移向量，左下角为 0 向量，右下角为 1 。这种矩阵又称为特殊欧氏群（ Special Euclidean Group ）：

$SE(3)=\left\{\boldsymbol{T}=\left[{\begin{array}{cc}R&t\\\\\mathbf{0}^T&1\end{array}}\right]\in\mathbb{R}^{4\times4}|\boldsymbol{R}\in SO(3),\boldsymbol{t}\in\mathbb{R}^3\right\}$

求解该矩阵的逆表示一个反向的变换：

$\boldsymbol{T}^{-1}=\left[\begin{array}{cc}\boldsymbol{R}^{T}&-\boldsymbol{R}^{T}\boldsymbol{t}\\\\\boldsymbol{0}^{T}&1\end{array}\right]$

旋转向量和欧拉角

旋转向量

矩阵表示方式的缺点

1. 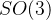$SO(3)$ 的旋转矩阵有九个量，但一次旋转只有三个自由度。因此这种表达方式是冗余的。同理，变换矩阵用十六个量表达了六自由度的变换。

2. 旋转矩阵自身带有约束：它必须是个正交矩阵，且行列式为 1。变换矩阵也是如此。要估计或优化一个旋转矩阵 / 变换矩阵时，这些约束会使得求解变得更困难。

旋转向量的定义

任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，可以使用一个向量，其方向与旋转轴一致，而长度等于旋转角。这种向量，称为旋转向量（或轴角，Axis-Angle ）。

假设有一个旋转轴为 $\boldsymbol{n}$ ，角度为 ${\theta}$ 的旋转，显然，它对应的旋转向量为 ${\theta}\boldsymbol{n}$ 。

旋转向量和旋转矩阵之间的转换

由旋转向量到旋转矩阵的过程由罗德里格斯公式（ Rodrigues’s Formula ）表明:

$\boldsymbol{R}=\cos\theta\boldsymbol{I}+(1-\cos\theta)\boldsymbol{n}\boldsymbol{n}^T+\sin\theta\boldsymbol{n}^\wedge$

其中，旋转轴 $\boldsymbol{n}$ 是矩阵 $\boldsymbol{R}$ 特征值1对应的特征向量。反之，我们也可以计算从一个旋转矩阵到旋转向量的转换:

$\begin{aligned} \operatorname{tr}\left(\boldsymbol{R}\right)& =\quad\cos\theta\text{tr}\left(\boldsymbol{I}\right)+\left(1-\cos\theta\right)\text{tr}\left(\boldsymbol{n}\boldsymbol{n}^T\right)+\sin\theta\text{tr}(\boldsymbol{n}^\wedge) \\ &=\quad3\cos\theta+(1-\cos\theta) \\ &\begin{array}{rcl}=&1+2\cos\theta.\end{array} \end{aligned}$

则有：

$\theta=\arccos(\frac{\operatorname{tr}(\boldsymbol{R})-1}2)$

欧拉角

它使用了三个分离的转角，把一个旋转分解成三次绕不同轴的旋转。欧拉角当中比较常用的一种，便是用“偏航-俯仰-滚转”（yaw-pitch-roll）三个角度来描述一个旋转的。

1. 绕物体的 Z 轴旋转，得到偏航角 yaw ；

2. 绕旋转之后的 Y 轴旋转，得到俯仰角 pitch ；

3. 绕旋转之后的 X 轴旋转，得到滚转角 roll 。

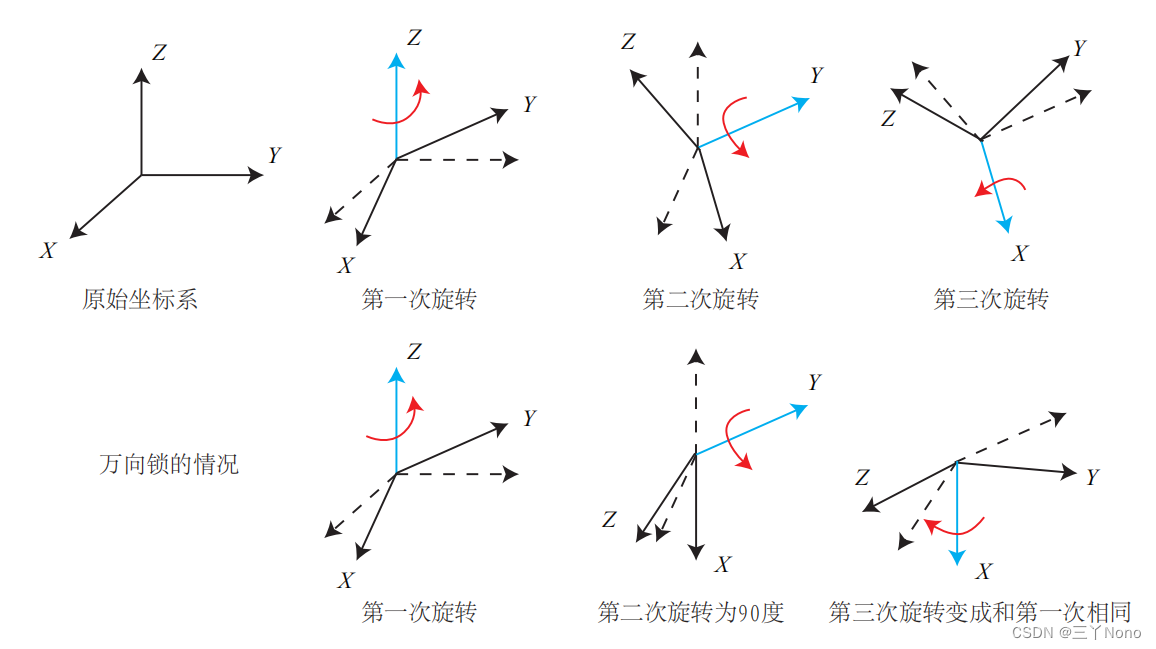
欧拉角的一个重大缺点是会碰到著名的 万向锁问题（Gimbal Lock）：在俯仰角为 $\pm90^{\circ}$ 时，第一次旋转与第三次旋转将使用同一个轴， 使得系统丢失了一个自由度（由三次旋转变成了两次旋转）。这被称为奇异性问题，在其他形式的欧拉角中也同样存在。

四元数

旋转矩阵用九个量描述三自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但具有奇异性。四元数是 Hamilton 找到的一种扩展的复数。 它既是紧凑的，也没有奇异性。如果说缺点的话，四元数不够直观，其运算稍为复杂一些。

四元数的形式

一个四元数 $\boldsymbol{q}$ 拥有一个实部和三个虚部：

$q=q_0+q_1i+q_2j+q_3k$

其中 $\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$ 为四元数的三个虚部。这三个虚部满足关系式：

$\begin{aligned}&i^2=j^2=k^2=-1\\&ij=k,ji=-k\\&jk=i,kj=-i\\&ki=j,ik=-j\end{aligned}$

也用一个标量（四元数的实部）和一个向量（四元数的虚部）来表达四元数：

$\boldsymbol{q}=[s,\boldsymbol{v}],\quad s=q_0\in\mathbb{R},\boldsymbol{v}=[q_1,q_2,q_3]^T\in\mathbb{R}^3$

四元数与旋转

在三维情况下,任意一个旋转都可以用单位四元数来描述,乘 $i$ 就是绕 $i$ 轴旋转180°。

假设某个旋转是绕单位向量 $\boldsymbol{n}=\left[n_x,n_y,n_z\right]^T$ ，进行了角度为 ${\theta}$ 的旋转，那么这个旋转的四元数形式为：

$\boldsymbol{q}=\left[\cos\frac\theta2,n_x\sin\frac\theta2,n_y\sin\frac\theta2,n_z\sin\frac\theta2\right]^T$

从单位四元数中计算出对应旋转轴与夹角：

$\begin{cases}\theta=2\arccos q_0\\\left[n_x,n_y,n_z\right]^T=\left[q_1,q_2,q_3\right]^T/\sin\frac{\theta}{2}\end{cases}$

${\theta}$ 加上 $2\pi$ ，我们得到一个相同的旋转，但此时对应的四元数变成了 $-\boldsymbol{q}$ 。因此，在四元数中，任意的旋转都可以由两个互为相反数的四元数表示。

把三维空间点用一个虚四元数来描述：

$\boldsymbol{p}=[0,x,y,z]=[0,\boldsymbol{v}]$

用四元数 $\boldsymbol{q}$ 表示这个旋转：

$\boldsymbol{q}=[\cos\frac\theta2,\boldsymbol{n}\sin\frac\theta2]$

那么，旋转后的点即可表示为这样的乘积：

$p^{\prime}=qpq^{-1}$

三丫Nono

关注

20
点赞
踩
19

收藏

觉得还不错? 一键收藏
0
评论
《视觉SLAM十四讲》公式笔记（ch03三维空间刚体运动)

任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，可以使用一个向量，其方向与旋转轴一致，而长度等于旋转角。这种向量，称为旋转向量（或轴角，Axis-Angle假设有一个旋转轴为，角度为的旋转，显然，它对应的旋转向量为。
复制链接

扫一扫