探索面板回归模型：内生性处理的策略与技巧（Stata进阶篇）

Stata进阶

本篇就来讲讲如何利用Stata来做实证分析，介绍具体操作的命令。实证分析用的数据通常为面板数据，因此文章以面板数据为例。在介绍之前，首先要了解什么是面板数据，面板数据指的是在一段时间内跟踪同一组个体的数据。它既有截面的维度（n位个体），又有时间维度（T个时期）。

一、面板数据模型的估计

对面板数据的估计，通常构建静态面板数据（指自变量没有时间滞后项/前推项的模型），对模型做进一步限制可以将面板数据模型划分为：混合回归模型、固定效应模型、随机效应模型。下面来一一介绍。

1、混合回归模型

混合回归模型假设从时间上看，不同个体之间不存在显著性差异；从截面上看，不同截面之间也不存在显著性差异，也可以理解为截距项和斜率都不随个体和时间的变化而变化，直接把面板数据混合在一起，用普通最小二乘法OLS估计参数。

reg y x1 x2 x3  //普通最小二乘回归

2、固定效应模型

对于面板数据，只有模型的截距项是不同的，而模型的斜率系数是相同的，并且允许截距项的变化（即个体的变化）与解释变量相关，则称此种模型为固定效应模型。固定效应模型又可以分为个体固定效应模型、时间固定效应模型和个体时间双向固定效应模型三种。

• 个体固定效应解决的是不随时间变化，但随个体变化的遗漏变量问题
• 时间固定效应解决的是不随个体变化，但随时间变化的遗漏变量问题

xtset id year //设定面板数据
//通常id为字符串变量，那么可以用以下命令转换为数值型变量
encode id,gen(ide) //这样变量ide就以1、2、3来代表不同个体
xtreg y x1 controls,fe //个体固定效应模型命令（默认固定个体）
xtreg y x1 x2 x3 i.year,fe //时间个体双固定效应模型命令（控制时间和个体）

//使用稳健标准误 
xtreg y x1 controls,fe robust  //个体固定效应模型命令
xtreg y x1 x2 x3 i.year,fe robust //时间个体双固定效应模型命令

3.随机效应模型

如果对于面板数据，只是模型的截距项是不同的，而模型的斜率系数是相同的，但是截距项的变化与解释变量不相关，则称此种模型为随机效应模型。同固定效应模型，随机效应模型可以分为个体随机效应模型、时间随机效应模型和个体时间双向随机效应模型三种。

xtreg y x1 x2 x3,re //个体随机效应模型命令
xtreg y x1 x2 x3 i.year,re //时间个体随机效应模型命令

4.豪斯曼检验

对于是否用固定效应还是随机效应模型，可用豪斯曼方法来检验，原假设为随机扰动项与解释变量x不相关，如果拒绝原假设，则选用固定效用模型。

//首先进行固定效应估计
xtreg y x1 x2 x3,fe   
estimates store FE //存储结果，名称为FE
//然后进行随机效应估计
xtreg y x1 x2 x3,re  
estimates store RE  
hausman FE RE,constant sigmamore  //豪斯曼检验

xtoverid //稳健的豪斯曼检验

5.最小二乘虚拟变量法（LSDV）

LSDV方法通过引入(n-1)个虚拟变量来代表不同个体，可以估计每个个体不随时间变化的变量的影响。

reg y x1 x2 x3 i.id //等同于xtreg y x1 x2 x3,fe命令

6.多维固定效应

在有些情况下，我们需要对三维甚至更高维度的数据进行分析 (例如，公司-年度-高管，省份-城市-行业-年度)，此时，可以考虑使用reghdfe命令。

ssc install gtools,replace
ssc install reghdfe,replace
reghdfe y x1 controls,absorb(id year) //控制个体、时间
reghdfe y x controls,absorb(id year industry) //控制个体、时间、行业

//使用稳健标准误
reghdfe y x controls,absorb(id year industry) vce(robust) //控制个体、时间、行业

xtreg、reg、reghdfe三种方法比较

命令	个体固定效应	时间固定效应
xtreg	fe	i.year
reg	i.id	i.year
reghdfe	absorb(id)	absorb(year)

建议个体固定效应使用xtreg，双向固定及多维固定效应使用reghdfe命令。

7.标准误的选择

• 普通标准误（独立同分布，同方差，不自相关）
• 异方差稳健标准误（异方差，不自相关）
• 聚类稳健标准误（异方差，自相关）
  括号里为具体出现相应问题，应采用的方法。

xtreg y x1 x2 x3 i.year,fe //普通标准误
xtreg y x1 x2 x3 i.year,fe robust //异方差稳健标准误
xtreg y x1 x2 x3 i.year,fe vce(cluster id) //聚类稳健标准误，以id名称进行聚类

8.实战

//导入消费与价格的数据后
reg consumption price // consumption与price回归
est store reg1
reg consumption price income  //consumption与price，income回归
est store reg2
reg consumption price income temp //consumption与price，income，temp回归
est store reg3

local m "reg1 reg2 reg3"
esttab reg1 reg2 reg3 using "C:\Users\86198\Desktop\结果.doc",se replace nogap scalars(r2_a aic bic N) star(* 0.1 ** 0.05 *** 0.01) b(%6.4f) //将结果导出为一个表格显示，要求系数的下方显示标准误

二、计量分析中内生性问题研究

在学习计量初级阶段，学习到的最小二乘法，即OLS，重要的基本假设中包含解释变量与扰动项不相关（不存在内生性），但在现实中，该条件往往是难以满足的，因此需要一些办法来解决内生性问题；

1.内生性的介绍

在计量经济学中，将所有与随机扰动项相关的解释变量都成为“内生变量”；具体描述可以用矩阵方程来展示，一般线性模型为：

产生内生性问题的原因主要有以下几点：

• 逆向因果关系
• 遗漏变量
• 测量误差

2.工具变量法

（1）使用条件
一个有效的工具变量应该满足两个条件：即工具变量与内生解释变量相关（相关性）、工具变量与扰动项不相关（外生性）；
工具变量法一般通过两阶段最小二乘法来估计，即2SLS，来实现，其基本原理主要是：进行两个回归来完成

• 第一阶段回归：将内生解释变量作为因变量，工具变量为自变量，进行回归，得到内生解释变量的拟合值；第一阶段目的主要是将内生解释变量进行分解，将内生部分与外生部分进行隔离开。
• 第二阶段回归：用被解释变量对第一阶段回归的拟合值进行回归

//两阶段最小二乘回归命令：ivregress
ivregress 2sls depvar [varlist1] (varlist2 = varlist_iv) [if] [in] [weight] [, options]`在这里插入代码片`

（2）工具变量的有效性检验
使用工具变量的提前是工具变量是有效性：

• 工具变量过度识别检验（检验工具变量的外生性）

ivregress 2sls lw s expr tenure rns smsa (iq=med kww),r first  //其中iq为内生变量，med与kww为工具变量
estimates store sls2
estat overid //过度识别检验：目的是考察是否所有工具变量都是外生的，即与扰动项不相关。若P值>0.1，则接受原假设，说明工具变量外生

注意：一般模型中可以包含多个回归变量（X）、多个外生变量（W）以及多个工具变量（Z），为了确保工具变量可行，工具变量（Z）的个数至少要和内生变量数目一样多。工具变量个数（m）与内生回归变量（k）个数关系可以描述为：当m=k时，则称回归系数恰好识别；当m>k时候，为过度识别；当m<k时候，为不可识别。要想估计工具变量回归，那么系数必须是恰好识别或过度识别的。

• 工具变量的相关性检验（弱工具变量检验）

estat firststage ,all forcenonrobust //关注第一阶段F值，F的P值较小<0.05，说明说明工具变量与内生变量是强相关的，满足工具变量的相关性要求。

解释较少X变化的工具变量称为弱工具变量，如果工具变量是弱的，那么2SLS（两阶段最小二乘法）不再可靠。那么检验方法为：在2SLS第一阶段，看F值，F统计量越大，工具变量包含的信息越多，一般大于10，那么无需担心若工具变量问题。

（3）ivreg2命令

ssc install ivreg2
ivreg2  lw s expr tenure rns smsa (iq=med kww),r orthong(med kww) first //orthong(med kww)检验工具变量是否满足外生性

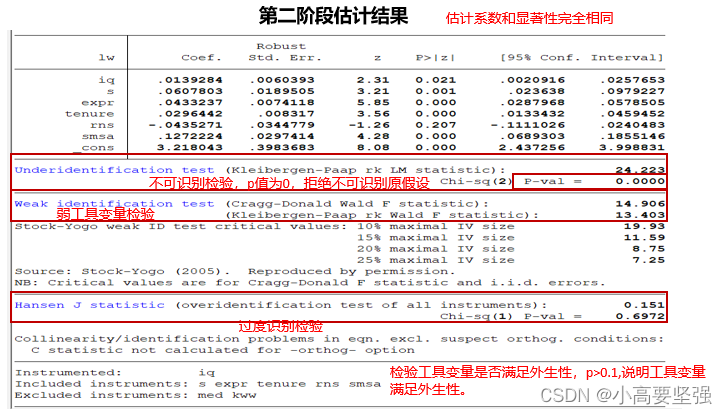
主要查看弱工具变量检验与过度识别检验来检验工具变量选取的是否合理。这里不可识别检验中P值为0，拒绝不可识别原假设。再来看，弱工具检验中的F值较大，通过检验。说明工具变量选取较为合理。

过度识别检验用来检验工具变量外生性：工具变量外生性，如何来检验，需要分情况，第一种情况是恰好识别情形，这种情况无法进行工具在事实上为外生的假设的统计检验，只能采用专家的建议以及你对该问题的经验认识。第二种情况是过度识别情形，则存在这一过程能够起到帮助作用的统计检验工具，即过度识别约束检验。如果P>0.1，则说明工具变量满足外生性。

过度识别约束检验：假设两个工具变量和一个内生变量，用两个工具进行估计得到两个系数，如果两个工具均为外生，那么它们会非常接近，如果不同，则可以有理由说明其中一个工具变量或这两个变量都不是外生的结论。

（4）多维固定效应模型的工具变量法

help ivreghdfe
ivreghdfe price weight (length=gear), absorb(rep78, tol(1e-6))