人工智能导论实验3——汉诺塔&八皇后问题

人工智能导论实验——汉诺塔&八皇后问题

实验目的及要求：
本项目要求能够理解人工智能的基本原理，理解问题归约法的原理和方法，掌握用问题归约表示问题的步骤，并能够实际问题给出具体的实现。
实验内容：
1.问题归约法的原理和方法
2.与或树表示问题的步骤
3.问题归约法的实现

一、汉诺塔问题

实验项目1：
已知3个柱子1，2，3和3个盘子A，B，C（A比B小，B比C小）。初始状态下，A，B，C依次放到1柱上。目标状态是A，B，C依次放在柱子2上。条件是每次可移动一个盘子，盘子上方是空顶方可移动，而任何时候都不允许大盘放在小盘之上。
实验要求：
1．形式化表示Hanoi问题，画出其规约图（即，与/或图）
2. 根据问题的形式化结果，结合prolog语言的特点，Prolog实现该问题求解；

实验步骤：
题目分析：
实现这个算法可以简单分为三个步骤：
①把n-1个盘子由柱1移到柱3；
②把第n个盘子由柱1移到柱2；
③把n-1个盘子由柱3移到柱2；

例如：
当n == 1时，
1.柱1---->柱2
sum = 1 次

当n == 2时，
2.柱1---->柱3
2. 柱1---->柱2
3. 4. 柱3---->柱2
sum = 3 次

当n == 3时，
4. 柱1---->柱2
5. 柱1---->柱3
6. 柱2---->柱3
7. 柱1---->柱2
8. 柱3---->柱1
9. 柱3---->柱2
10. 柱1---->柱2
sum = 7 次

其状态图如下：

prolog代码如下：

hanoi(N) :- move(N,left,center,right).
move(0,_,_,_) :- !.
move(N,A,B,C) :-
    M is N-1,
    move(M,A,C,B),
    inform(A,B),
    move(M,C,B,A).

inform(X,Y) :- write('Move from '), write(X), write(' to '), write(Y), write('.'), nl.

运行结果如下：

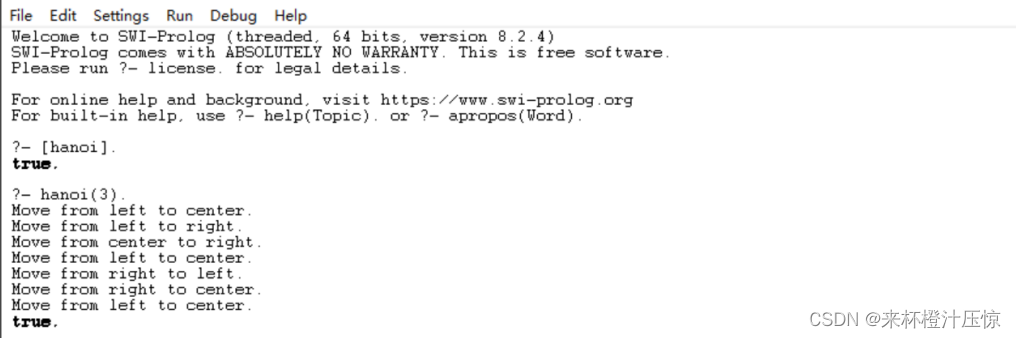
二、八皇后问题

实验项目2：
如何能在8*8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇
后？为了到达此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。
通过实验，基本掌握逻辑编程的思想，了解逻辑编程与命令式编程的区别。
能够依据给定的事实以及规则编写代码，解决逻辑约束问题(CLP)。

实验要求：

1. 画出求解8皇后问题的递归回溯算法和迭代算法流程图。
2. 画出状态树（任意解均可）。
3. 参考华为《人工智能导论》实验手册，在华为云的ModelArts中用Python实现该问题的求解。

实验步骤：
算法介绍：
回溯算法：回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，