正态分布定义
正态分布(Normal Distribution),又名高斯分布(Gaussian Distribution)。若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
标准差:
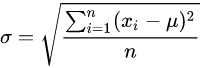
若随机变量 X 服从一个位置参数为 μ、尺度参数为 σ 的概率分布,且其概率密度函数为



标准化
小明每天上学的通勤时间是一个随机变量X,这个变量服从正态分布。统计他过去20天的通勤时间(单位:分钟):26、33、65、28、34、55、25、44、50、36、26、37、43、62、35、38、45、32、28、34。现在我们想知道他上学花30~45分钟的概率。
求解期望μ以及方差σ
import numpy as np
datas = np.array([26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32, 28, 34])
print(datas.mean(), datas.std())
38.8 11.399999999999999
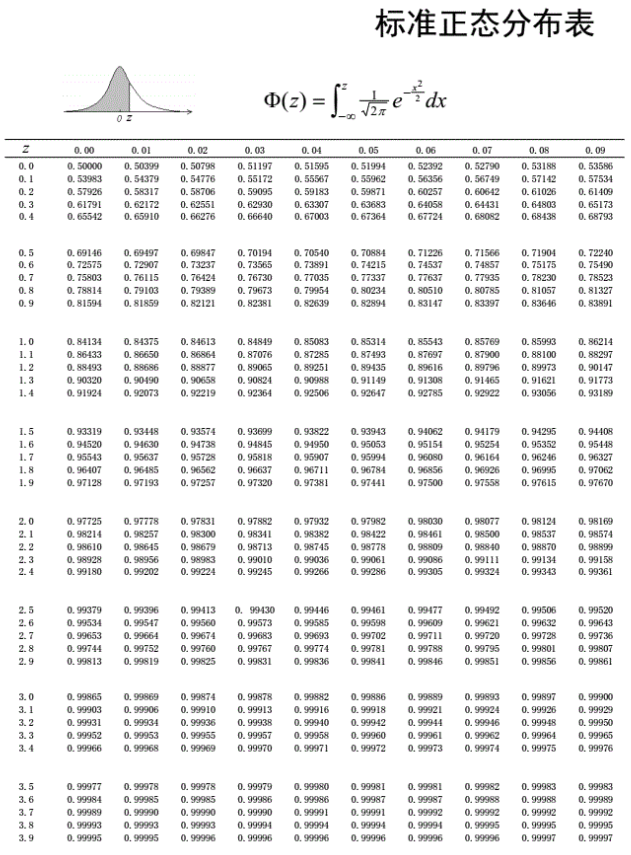
求P(30 < X < 45),就转换成了求P(-0.77 < Z < 0.54),标准化的具体计算为:
- 30 →(30-38.8)/ 11.4 = - 0.77
- 45 →(45-38.8)/ 11.4 = 0.54
- X → Z
- P(30 ≤ X ≤ 45)= P(-0.77 ≤ Z ≤ 0.54)
- P (-0.77 ≤ Z ≤0.54) = P (Z ≤ 0.54) – P (Z ≤ -0.77)
标准正态分布








 本文介绍了正态分布的概念,包括其定义、期望值μ和标准差σ的作用。通过一个实际例子展示了如何对一组数据进行标准化处理,将通勤时间从原始分布转换为标准正态分布,并计算了在30到45分钟之间的概率。标准化是统计分析中常用的数据预处理方法,便于比较不同分布的数据。
本文介绍了正态分布的概念,包括其定义、期望值μ和标准差σ的作用。通过一个实际例子展示了如何对一组数据进行标准化处理,将通勤时间从原始分布转换为标准正态分布,并计算了在30到45分钟之间的概率。标准化是统计分析中常用的数据预处理方法,便于比较不同分布的数据。

















 1116
1116

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










