求局域最小值的方法 学习笔记（2）

拟牛顿法的提出以及拟牛顿条件

虽然牛顿法具有最速下降法所无法匹敌的下降的速度，但是有着几个非常明显的缺陷：
1. 若Hessian矩阵不是正定矩阵，则会出现搜索方向可能不是函数的下降方向，使得函数不降反升。
2. 若函数不存在二阶连续导数，则无法使用牛顿法求解
3. 计算Hessian矩阵较为繁琐

在此基础上，人们提出了拟牛顿法，核心思想是构造矩阵$A^{(k)}$，在每一步的迭代过程中都不断修改$A^{(k)}$，最终使之逼近海森矩阵的逆矩阵。在此基础上，每次迭代的方向为
$${\vec{d}}_k=-A^{(k)}\nabla f(x_k)$$
当$A^{(k)}=E$时，迭代搜索的方向就是梯度下降法的方向；当$A^{(k)}=H^{-1}$时，迭代搜索方向就是牛顿法的方向
构造$A^{(k)}$时，应该具有如下性质：

1. 正定性：函数下降方向为$-\nabla f(x)$，为使搜索方向也为下降方向，应有$$-{\vec{d}}^T\nabla f(x)=\nabla f(x{)}^T{A}^{(k)}\nabla f(x)>0$$即$A^{(k)}$具有正定性。
2. 收敛于$H^{-1}$或$H$：为使得该方法具有牛顿法的下降速度，需使得$A^{(k)}$收敛于$H$或其逆矩阵
3. 计算方便。

接下来分析如何构造$A^{(k)}$：
将$f(x)$展开，有：
$$f(x_k+x)=f(x_k)+x^T\nabla f(x_k)+\frac{1}{2}{x}^{T}Hx$$
那么在$x_{k+1}$处，其梯度满足:
$$\nabla f(x_{k+1})=\nabla f(x_k)+H_k(\Delta x_k)$$
令$\nabla f(x_{k+1})=g(x_{k+1}),\nabla f(x_k)=g(x_k)$，有：
$$\begin{gathered} \Delta g_k=H_k\Delta x_k \\ \Delta x_k=H_k^{-1}\Delta g_k \end{gathered}$$
选用下面的式子做为逼近条件，即用$A^{(k+1)}$逼近$H_k^{-1}$，得到$A^{(k+1)}$满足的条件：
$$\Delta x_k=A^{(k+1)}\Delta g_k$$
上式称为拟牛顿条件。

DFP法

令$A^{(k+1)}=A^{(k)}+E^{(k)}$，即认为$A^{(k+1)}$是由上一个$E^{(k)}$加上修正矩阵${\Delta }^{(k)}$得来，那么所求改为修正矩阵。带入拟牛顿条件有：
$$E^{(k)}\Delta g_k=\Delta x_k-A^{(k)}\Delta g_k$$
由于需要$E^{(k)}$对称，故设$E^{(k)}=\alpha u{u}^T+\beta v{v}^T,u=\Delta x,v=A^{(k)}\Delta g_k.$
右乘$\Delta g_k$,有：
$$E^{(k)}\Delta g_k=\alpha u(u^T\Delta g_k)+\beta v(v^T\Delta g_k)$$
结合拟牛顿条件，不难得到：
$$\alpha =\frac{1}{(u^T\Delta g_k)},\beta =-\frac{1}{(v^T\Delta g_k)}$$
带入即得$E^{(k)}$，进一步得$A^{(k+1)}$:
$$A^{(k+1)}=A^{(k)}+\frac{\Delta x\Delta x^T}{(\Delta x^T\Delta g_k)}-\frac{A^{(k)}\Delta g_k\Delta g_k^T{A}^{(k)T}}{(\Delta g_k^T{A}^{(k)}\Delta g_k)}$$
若我们初始$A^0$取单位矩阵，其也满足对称以及正定性，而且迭代时第一步就是最速下降法。

BFGS法

若用$A^{(k+1)}$逼近$H_k$，得到$A^{(k+1)}$满足的条件：
$$\Delta x_k=A^{(k+1)}\Delta g_k$$
仿照上面推导过程可以的到：
$$A^{(k+1)}=A^{(k)}+\frac{\Delta g\Delta g^T}{(\Delta x^T\Delta g_k)}-\frac{A^{(k)}\Delta x_k\Delta x_k^T{A}^{(k)T}}{(\Delta x_k^T{A}^{(k)}\Delta x_k)}$$
同理取$A^0$为单位矩阵，第一步为最速下降法。

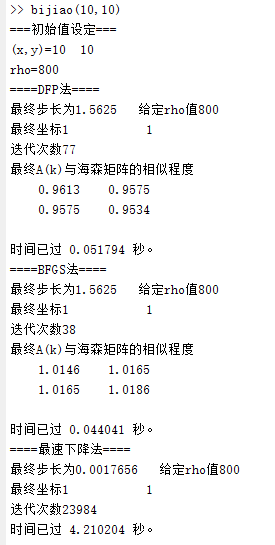
结果