2025-11-20：买卖股票的最佳时机Ⅴ。用go语言，给定一个整数数组 prices（prices[i] 表示第 i 天的股票价格），以及一个整数 k。你最多可以执行 k 笔交易，每笔交易有两种形式

原创于 2025-11-20 01:00:00 发布 · 619 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#golang #java #开发语言

福大大架构师每日一题专栏收录该内容

1665 篇文章

订阅专栏

开源AI·十一月创作之星挑战赛 10w+人浏览 398人参与

2025-11-20：买卖股票的最佳时机Ⅴ。用go语言，给定一个整数数组 prices（prices[i] 表示第 i 天的股票价格），以及一个整数 k。你最多可以执行 k 笔交易，每笔交易有两种形式：

正向交易（先买后卖）：在某天 i 买入，在之后的某天 j 卖出（i < j），该笔交易的收益为 prices[j] − prices[i]。
做空交易（先卖后买回）：在某天 i 先卖出，之后在某天 j 买回（i < j），该笔交易的收益为 prices[i] − prices[j]。
约束条件：
每次交易必须在前一笔交易完成后才能开始，交易之间不能重叠；
同一天内不能同时进行买入和卖出操作。

目标是在不超过 k 笔交易的前提下，使总收益最大化，返回该最大可能的累计收益。

2 <= prices.length <= 1000。

1 <= prices[i] <= 1000000000。

1 <= k <= prices.length / 2。

输入: prices = [12,16,19,19,8,1,19,13,9], k = 3。

输出: 36。

解释:

我们可以通过 3 笔交易获得 36 美元的利润：

一笔普通交易：第 0 天以 12 美元买入，第 2 天以 19 美元卖出。
一笔做空交易：第 3 天以 19 美元卖出，第 4 天以 8 美元买回。
一笔普通交易：第 5 天以 1 美元买入，第 6 天以 19 美元卖出。

题目来自力扣3573。

程序过程详细描述

状态定义：
- 程序使用一个二维数组 f，其维度为 (k+2) x 3。其中：
  - f[j][0] 表示在完成最多 j 笔交易后，当前处于“空闲状态”（不持有任何头寸）时的最大收益。
  - f[j][1] 表示在完成最多 j 笔交易后，当前持有“多头头寸”（已买入股票但未卖出）时的最大收益。
  - f[j][2] 表示在完成最多 j 笔交易后，当前持有“空头头寸”（已卖空股票但未买回）时的最大收益。
- 索引 j 的范围是 0 到 k+1，其中 j=0 表示未进行任何交易，j=k+1 是为了覆盖最多 k 笔交易的边界情况。
初始化：
- 将 f 数组的初始值设置为一个极小的负数（math.MinInt / 2），表示不可能状态或未初始化状态。
- 特别地，f[0][0] 也被初始化为极小负数，但实际初始状态（0笔交易、空闲状态）的收益应为0，不过程序通过后续更新覆盖此值。
遍历价格数组：
- 对于每一天的价格 p，程序逆序更新 j 从 k+1 到 1（逆序是为了避免状态覆盖，确保使用前一天的数据）。
- 对于每个 j，更新三个状态：
  - 更新空闲状态（f[j][0]）：
    - 可能来自三种情况：
      - 保持空闲：f[j][0] 自身。
      - 从多头头寸平仓：卖出持有的股票，收益增加 p，即 f[j][1] + p。这完成了一笔正向交易（但交易次数 j 不变，因为交易次数在开仓时已计算）。
      - 从空头头寸平仓：买回股票平仓，收益减少 p，即 f[j][2] - p。这完成了一笔做空交易。
    - 取这三种情况的最大值。
  - 更新多头头寸状态（f[j][1]）：
    - 可能来自两种情况：
      - 保持多头头寸：f[j][1] 自身。
      - 从空闲状态开仓买入：在空闲状态下买入股票，开始新交易。收益减少 p，并从 j-1 笔交易的状态转移，即 f[j-1][0] - p。这里 j-1 到 j 表示开仓操作占用了一笔交易次数。
  - 更新空头头寸状态（f[j][2]）：
    - 类似地，可能来自：
      - 保持空头头寸：f[j][2] 自身。
      - 从空闲状态开仓做空：在空闲状态下卖出股票（做空），开始新交易。收益增加 p，即 f[j-1][0] + p，交易次数从 j-1 增加到 j。
状态转移的核心：
- 开仓操作（买入或做空）会增加交易次数 j，并从空闲状态转移。
- 平仓操作（卖出或买回）不改变 j，但将头寸转为空闲状态。
- 交易不能重叠，因此任何时候最多持有一个头寸（多头或空头）。
返回结果：
- 遍历所有价格后，返回 f[k+1][0]，表示在最多进行 k 笔交易后处于空闲状态的最大收益。这里使用 k+1 是为了确保覆盖所有交易次数，因为初始化时 j 从 0 开始。

时间复杂度和空间复杂度

时间复杂度：程序需要遍历价格数组中的每个价格（长度为 n），对于每个价格，逆序遍历 j 从 k+1 到 1（共 k 次循环）。因此，总时间复杂度为 O(n × k)。
空间复杂度：程序维护了一个二维数组 f，大小为 (k+2) × 3。由于 k 是输入参数且 k ≤ n/2，额外空间复杂度为 O(k)（与 n 无关，但受 k 限制）。

该动态规划方法通过状态机模型高效处理了两种交易类型，确保了在约束下最大化收益。

Go完整代码如下：

package main

import (
	"fmt"
	"math"
)

func maximumProfit(prices []int, k int) int64 {
	f := make([][3]int, k+2)
	for j := 1; j <= k+1; j++ {
		f[j][1] = math.MinInt / 2
		f[j][2] = math.MinInt / 2
	}
	f[0][0] = math.MinInt / 2
	for _, p := range prices {
		for j := k + 1; j > 0; j-- {
			f[j][0] = max(f[j][0], f[j][1]+p, f[j][2]-p)
			f[j][1] = max(f[j][1], f[j-1][0]-p)
			f[j][2] = max(f[j][2], f[j-1][0]+p)
		}
	}
	return int64(f[k+1][0])
}

func main() {
	prices := []int{12, 16, 19, 19, 8, 1, 19, 13, 9}
	k := 3
	result := maximumProfit(prices, k)
	fmt.Println(result)
}

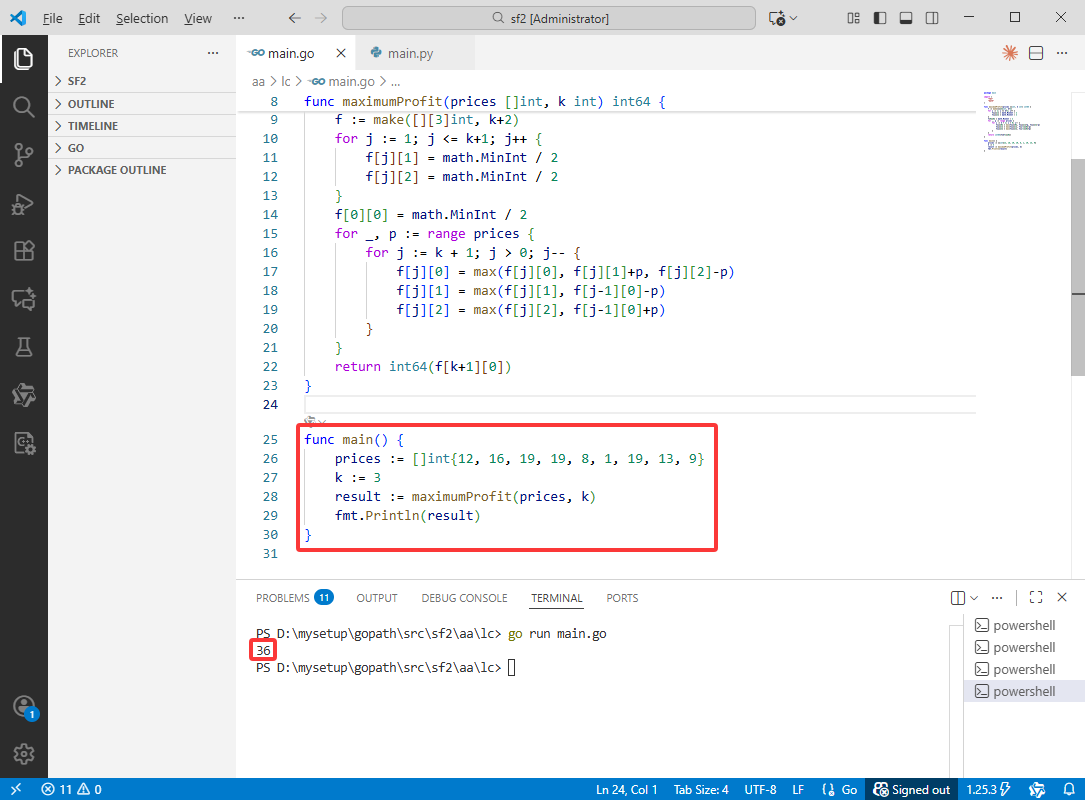
在这里插入图片描述

Python完整代码如下：

# -*-coding:utf-8-*-

import math

def maximumProfit(prices, k):
    # 初始化动态规划数组
    # f[j][0]: 空仓状态的最大利润
    # f[j][1]: 持有第一支股票状态的最大利润  
    # f[j][2]: 持有第二支股票状态的最大利润
    f = [[0] * 3 for _ in range(k + 2)]
    
    # 初始化状态
    for j in range(1, k + 2):
        f[j][1] = -10**18  # 使用一个很大的负数代替math.MinInt
        f[j][2] = -10**18
    f[0][0] = -10**18
    
    # 动态规划处理每个价格
    for p in prices:
        # 从后往前更新，避免状态覆盖
        for j in range(k + 1, 0, -1):
            # 更新空仓状态：保持空仓、卖出第一支、卖出第二支
            f[j][0] = max(f[j][0], f[j][1] + p, f[j][2] - p)
            # 更新持有第一支股票状态：保持持有、从空仓买入
            f[j][1] = max(f[j][1], f[j-1][0] - p)
            # 更新持有第二支股票状态：保持持有、从空仓买入
            f[j][2] = max(f[j][2], f[j-1][0] + p)
    
    return f[k+1][0]

# 测试代码
if __name__ == "__main__":
    prices = [12, 16, 19, 19, 8, 1, 19, 13, 9]
    k = 3
    result = maximumProfit(prices, k)
    print(result)

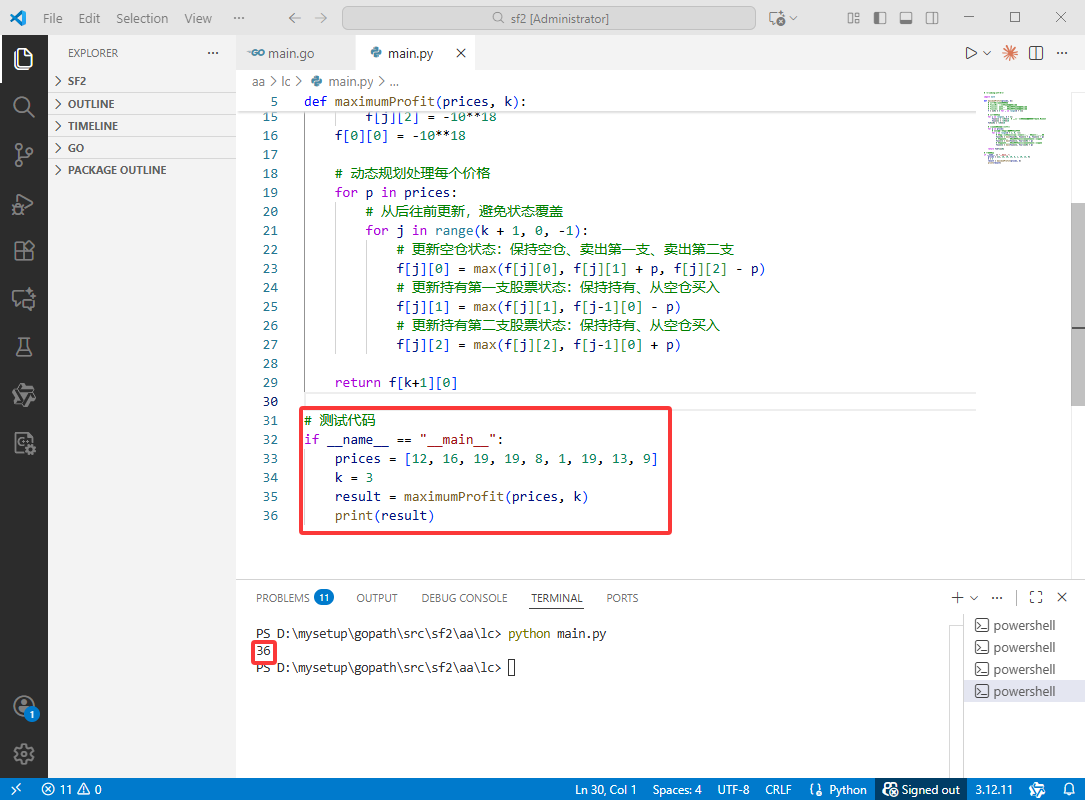
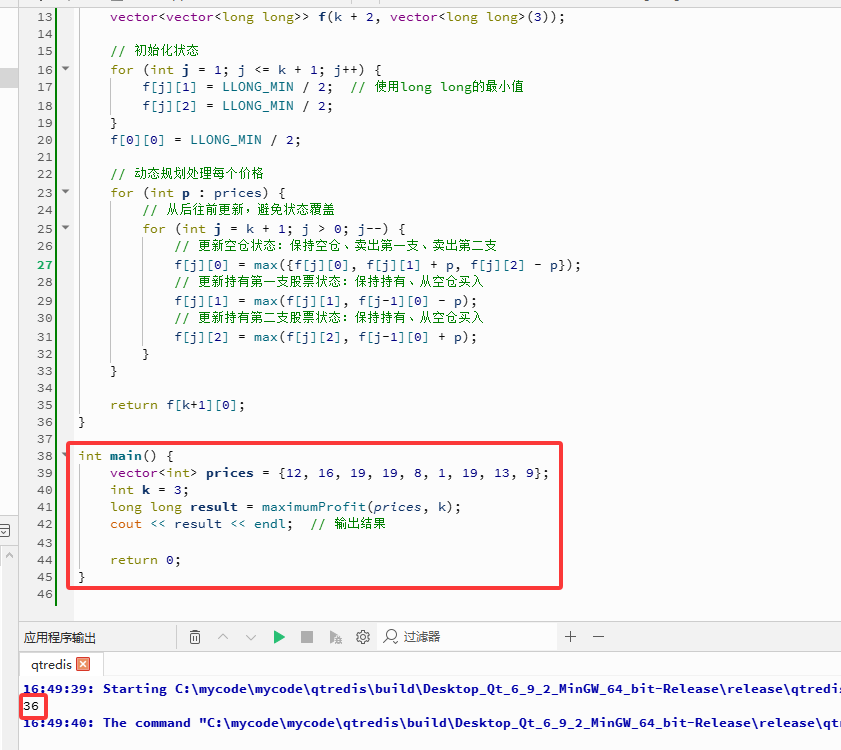
在这里插入图片描述

C++完整代码如下：

#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>

using namespace std;

long long maximumProfit(vector<int>& prices, int k) {
    // 初始化动态规划数组
    // f[j][0]: 空仓状态的最大利润
    // f[j][1]: 持有第一支股票状态的最大利润
    // f[j][2]: 持有第二支股票状态的最大利润
    vector<vector<long long>> f(k + 2, vector<long long>(3));

    // 初始化状态
    for (int j = 1; j <= k + 1; j++) {
        f[j][1] = LLONG_MIN / 2;  // 使用long long的最小值
        f[j][2] = LLONG_MIN / 2;
    }
    f[0][0] = LLONG_MIN / 2;

    // 动态规划处理每个价格
    for (int p : prices) {
        // 从后往前更新，避免状态覆盖
        for (int j = k + 1; j > 0; j--) {
            // 更新空仓状态：保持空仓、卖出第一支、卖出第二支
            f[j][0] = max({f[j][0], f[j][1] + p, f[j][2] - p});
            // 更新持有第一支股票状态：保持持有、从空仓买入
            f[j][1] = max(f[j][1], f[j-1][0] - p);
            // 更新持有第二支股票状态：保持持有、从空仓买入
            f[j][2] = max(f[j][2], f[j-1][0] + p);
        }
    }

    return f[k+1][0];
}

int main() {
    vector<int> prices = {12, 16, 19, 19, 8, 1, 19, 13, 9};
    int k = 3;
    long long result = maximumProfit(prices, k);
    cout << result << endl;  // 输出结果

    return 0;
}