贝叶斯决策理论

贝叶斯决策理论的相关知识

贝叶斯的思想：顾名思义，贝叶斯决策论是利用概率来进行决策，是概率框架下的方法。贝叶斯决策论是利用概率的不同分类决策与相应的决策代价之间的平衡，核心思想是决策问题可以通过概率的形式来描述。

1.表示法

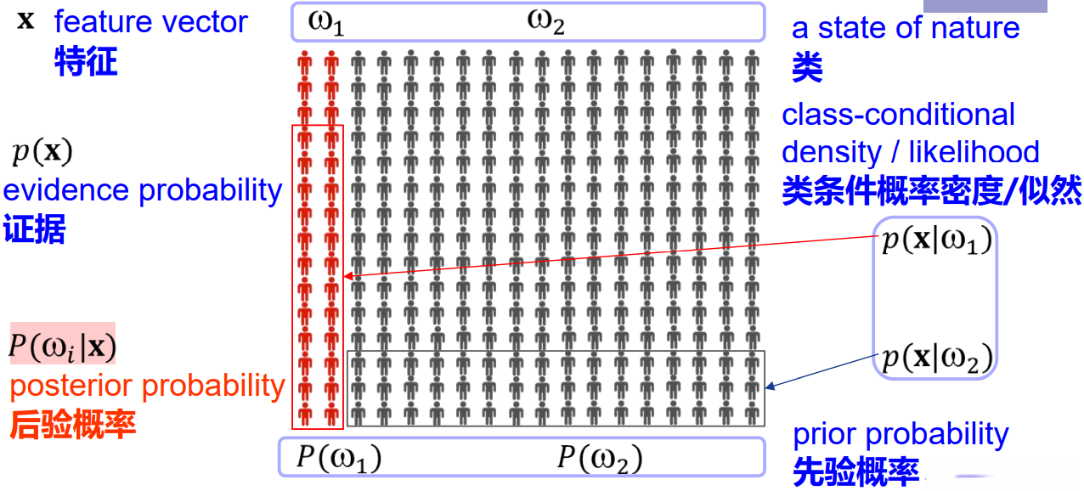
假定x是一个连续随机变量，其分布取决于类别状态，表示为  的形式，这就是类条件概率密度，即类别状态为  时的x的概率密度函数。通俗的理解：分类作为概率密度函数的条件。

2 贝叶斯分类

假设我们要对一种物体进行分类，只根据它的先验概率p(w)分类是不现实的，若某种类型的先验概率较大，那么几乎所有物体都会被判别为那种类型，这显然是错误的。

为了更好的进行分类，我们观察事物的一些特征X，例如对于鱼分类——鱼的光泽程度，对西瓜分类——西瓜的颜色。统计了关于特征x的类条件概率密度。根据贝叶斯公式：

Pωj∣x=px∣ωjPωjp(x) 表明，通过观测x的值我们可以将先验概率转换为后验概率，即假设特征值x已知的条件下类别为wj的概率。

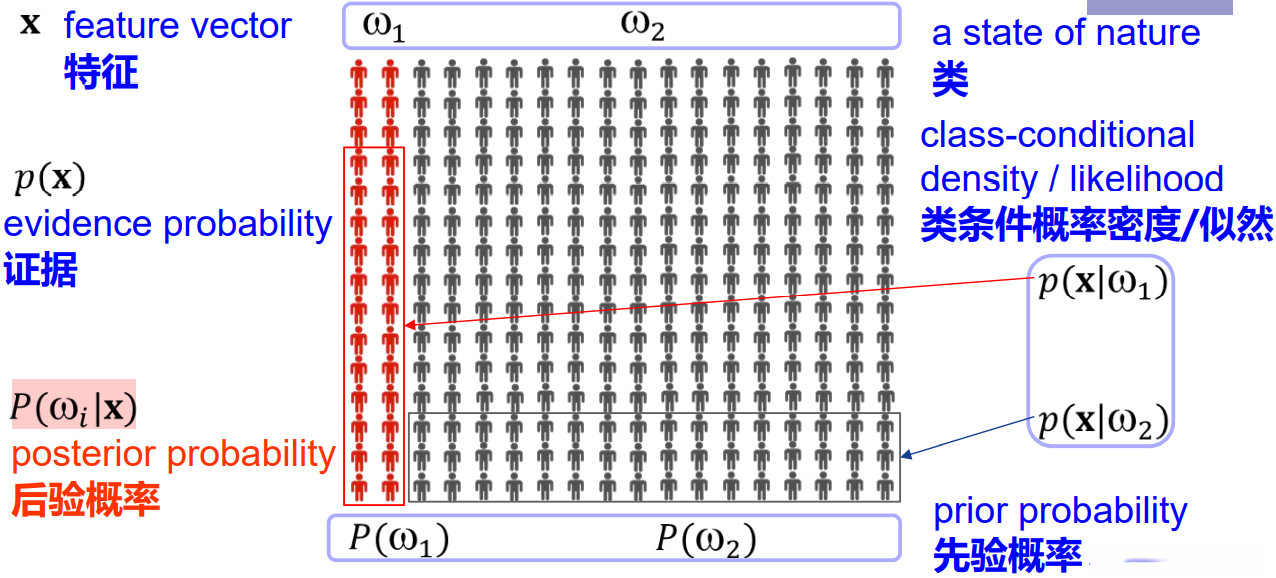
上图是一个二分类问题，可以看到右图中每个横坐标下对应的后验概率之和为1

我们可以初步的利用后验概率进行分类。

3 贝叶斯决策理论

贝叶斯决策：在类条件概率密度和先验概率已知的情况下，通过贝叶斯公式比较样本属于两类的后验概率，为使总体错误率最小，将类别决策为后验概率大的一类。

Pωi∣X=PX∣ωiPωiP(X)

3.1 最小误差概率决策

最小错误率：Pωk∣x=maxi=1,2 Pωi∣x, 则 x∈ωk

平均错误概率P(e): P(e)=∫P(e∣x)P(x)dx

根据第2节的内容，如果有某个观测值x使得  我们自然的会做出真实类别是w1的判断，我们计算做出某次分类判决时的误差概率：

        对于特殊的二分类问题，我们有：

P( error ∣x)=&Pω2∣x    && if we decide ω1&Pω1∣x    && if wedecide ω2

可验证得到，这种规则可以将平均误差概率最小化。因此，我们得到了最小化误差概率条件下的贝叶斯决策规则：对于二分类问题       

注意到在贝叶斯公式中，分母证据因子p(x)对于做出某种决策并不重要，表示我们实际测量的具有特征x的模式的出现概率，实际问题中可以忽略。

3.2 连续特征下的最小化风险决策

将不同类分错造成的后果的严重性并不总是一样的，于是要设计分类规则使得损失（风险）最低

对于3.1所讨论的问题我们推广到以下四种情况：

• 有多于一个特征x
• 多种类别状态
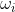
• 允许有其他的行为而不仅仅是判别类型
• 引入一个更一般损失函数来代替误差概率p(error)

计算后验概率的贝叶斯公式将一维的特征x推广到多维x向量：（证据因子  ）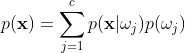

假定我们观测某个特定模式x并且采取行动  ，如果真实的类别状态为  ，通过定义我们将有损失  。既然  是实际类别状态为  时的概率，与行为  相关联的损失——条件风险：

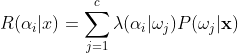
回到最初的问题，我们希望找到一种替代  的决策规则以最小化总风险，我们设为观测某个特征的向量形式x而采取的行动，总风险R：

——此积分是在整个特征空间进行的

 因此我们得出最小化风险决策的贝叶斯决策规则：为了最小化总风险，对所有的 i = 1,2...,a 计算条件风险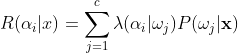： 并且选择  使   最小化。最小化后的总风险记为R*，叫做贝叶斯风险，他是可获得的最优结果。

3.2.1  0-1 损失函数下的风险函数

假设采取行为为而实际类别为，那么在i=j的情况下判决时正确的，如果i != j 则定义为误判，当我们采用0-1损失函数/对称损失函数：

这个损失函数将0损失赋给一个正确的判断，而将一个单位损失赋给任何一个错误判决，所有误判代价都是等价的，这种情况下的条件风险为：

  Rαi∣x=j=1c λαi∣ωjPωj∣x=j≠i Pωj∣x=1-Pωi∣x

这种情况下我们想最小化风险只要选取i使得后验概率最大即可。

3.2.2两类分类问题

考虑将最小化风险决策运用到两类分类问题时，简化以 表示当实际类型为 时误判为  所引起的损失。自然得到以下结论：

最小风险和最小错误率贝叶斯决策法则的关系：

两类最小错误率贝叶斯决策规则

Pω1∣x⩾Pω2∣x,∋x∈&ω1&ω2

多类最小错误率贝叶斯决策规则

Pωk∣x=maxi=1,…,c Pωi∣x,∋x∈ωk

多类最小风险贝叶斯决策规则

Rαk∣x=mini=1,…,c j=1c λjiPωj∣x,∋α=αk

关系：当损失函数为 0 − 1 0-10−1 损失函数 Cannot read properties of undefined (reading 'type') 时，最小风险贝叶斯决策就变成了最小错误率贝叶斯决策。即后者时前者的一个特例。