什么是二次曲面？什么是三次曲面？（含曲面算法公式）

二次曲面和三次曲面是数学和计算机图形学中的基本概念，它们分别代表不同阶数的代数曲面。以下是它们的定义、特点和常见例子。

1. 二次曲面（Quadratic Surface）

定义：二次曲面是由二次方程定义的曲面，其标准形式为：

其中 A, B, C, D, E, F, G, H, I, JA,B,C,D,E,F,G,H,I,J 是常数。二次曲面可以看作是三维空间中的曲面，通常由二次多项式的线性组合形成。

特点：

• 形状多样：二次曲面可以呈现多种形状，包括椭圆、抛物线和双曲线等。
• 平滑性：二次曲面在其定义域内通常是平滑的，没有尖点或折角。

常见的二次曲面例子：

• 椭球面：标准方程为 ，其中 a, b, ca,b,c 为半轴长。
• 抛物面：标准方程为 ，表现为一个开口向上的曲面。
• 双曲面：标准方程为 ，表现为一个双曲线的旋转体。

2. 三次曲面（Cubic Surface）

定义：三次曲面是由三次方程定义的曲面，其标准形式为：

其中 A, B, C, D, E, F, G, H, I, J, K, L, M, NA,B,C,D,E,F,G,H,I,J,K,L,M,N 是常数。

特点：

• 更复杂的形状：三次曲面比二次曲面具有更高的灵活性和复杂性，可以表达更加复杂的几何形状。
• 光滑性：三次曲面通常是光滑的，具有较好的视觉效果。

常见的三次曲面例子：

• 三次贝兹曲面：常用于计算机图形学中的建模和曲面设计，尤其在CAD软件和动画制作中。
• B样条曲面：广泛应用于计算机图形学中的曲线和曲面建模。
• 多项式曲面：在数值分析和数据拟合中，经常使用三次多项式来进行数据插值。

小结

• 二次曲面：由二次多项式定义，形状较简单，包含椭球、抛物面和双曲面等。
• 三次曲面：由三次多项式定义，形状更复杂，能表示更丰富的几何形状，常用于现代计算机图形学和建模。

---

        我们可以用简单的语言和比喻来解释二次曲面和三次曲面的概念，以及它们的公式。

二次曲面

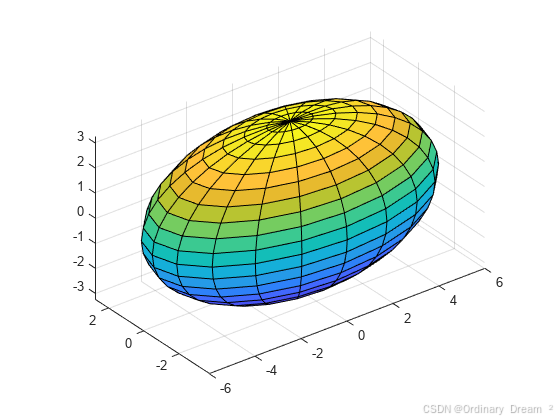
想象一下一个气球！
当你把气球充气时，气球的表面会变得圆圆的。这种形状就是一种叫做椭球面的二次曲面。

二次曲面的简单公式

我们可以用一个很简单的数学表达式来描述椭球的形状，像这样：

    

• x, y, z：就像我们在空间中找东西的位置。
• a, b, c：就像气球的不同方向的长度（比如，气球的宽度、高度和深度）。

常见的二次曲面例子

1. 椭球：就像你充气的气球。
2. 抛物面：想象一个碗的形状。我们可以用一种叫做抛物线的形状来描述。
3. 双曲面：可以想象一个沙漏的形状，上面和下面是两个开口的部分。

三次曲面

现在想象一个沙滩上的小山！
如果你在沙滩上用手指做一个小山，那个小山的形状就可以用一种叫做三次曲面的东西来描述。

三次曲面的简单公式

三次曲面的表达式会更复杂，但我们可以想象成是这样：

• x 和 y：就像在沙滩上找地方。
• A 和 B：这些是帮助我们确定小山形状的“助手”。

常见的三次曲面例子

1. 三次贝兹曲面：就像用粘土做出的复杂形状，可以弯曲得很好。
2. B样条曲面：就像滑滑梯的形状，平滑而弯曲。
3. 多项式曲面：想象你在地图上画的山脉，可以有很多起伏。

小结

• 二次曲面：像气球、碗和沙漏，形状简单。
• 三次曲面：像沙滩上的小山，形状复杂。