期末考试考点:
目录
11.2 双边Z-变换((Two-sided) z-transform)
11.2.2 序列变成多项式(Sequence becomes a polynomial)
11.3.1 指数衰减练习(11.3.1 Exponential decay exercise)
11.4 Z变换的性质(Properties of the z-transform)
第12章:Introduction to Digital Filtering
12.2 数字滤波器方程(Digital filter equation)
12.3.1 多项式的系数(Ratio of polynomials)
12.3.2 极点和零点 (Poles and zeros)
12.3.2.1 零极点图(Pole-zero diagram)(重点!!!)
12.3.3 实系数多项式(Polynomials with Real coefficients)
12.3.4 实系数滤波器 (Filters with real coefficients)
12.4.1 模拟信号的数字滤波(Digital filtering of an analog signal)
第13-15章:Finite Impulse Response(FIR)filter
13.2.2 阶跃响应(Unit step response)
13.2.3 转换方程(Transfer function)
13.3.3 对正弦波@1/4fs的响应(sine wave)
13.3.4 对余弦波@ 1/2fs的响应(cosine wave)
13.3.5 传递函数(Transfer function)
14.2 实滤波器的充分条件(Sufficient conditions for real filters)
14.2.2.1 偶数个系数(An even numbe of coefficients)
14.2.2.2 奇数个系数(An odd numbe of coefficients)
14.2.3 结论(Conclusion)(究极重要!!!!)
15.3.2 窗口类型(Windowing procedure)
前言:
本笔记是基于北京都柏林学院2022年EEEN3004J Digital Signal Process课程课件总结出的笔记。任课教师为Dr John Healy。
第11章:The z-transform
11.1 背景(Backgournd)
对于连续时间系统,我们有傅里叶变换和(双面)拉普拉斯变换-为什么两者都有?让我们看看它们的定义:
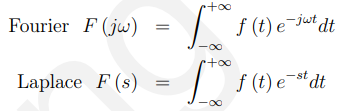
其中,拉普拉斯变换![]()
它们之间的主要区别是,在拉普拉斯变换中,变量s = σ + jw是任意复数,而傅里叶变量w是纯实数。这种改变使得无限复正弦曲线的和之外的解存在。
稳态系统的解可以用复数正弦项的和来表示,例如 对于
,但是暂态系统的解需要更复杂的公式,不能简单地用
项来表示,因此拉普拉斯变量
![]() 包含额外的
包含额外的项,从而允许解有指数衰减(或增加)项,即
![]() 。
。
显然,如果,则这一项趋近于0即t趋近于无穷,解收敛于某些稳态条件(暂态效应消失)。
RC电路练习题(重点之一)
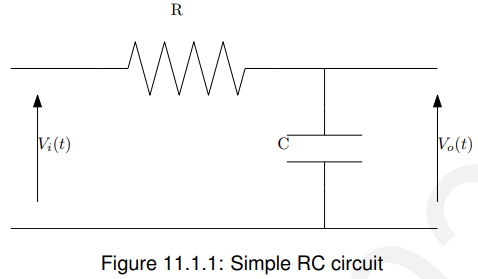
这个电路的傅里叶分析允许我们计算输出(无限长)正弦信号,当有(无限长)正弦信号输入时:
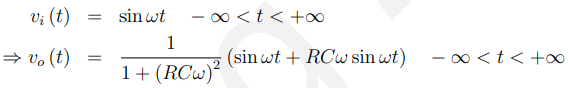
过程:
让 ,
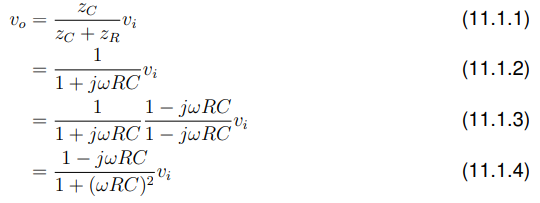
然后让 ![]()
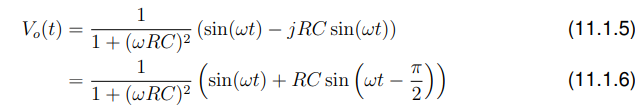
现在我们已经用傅里叶变换计算出了输出。但是,如果t < 0时,输入(t) = vo (t) = 0,即电路在t = 0时“接通”,并且假设在此时间之前所有电压都为零,该怎么办?,即
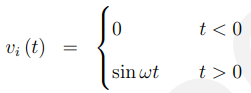
傅里叶分析结果不再有效
拉普拉斯变换得到以下结果:
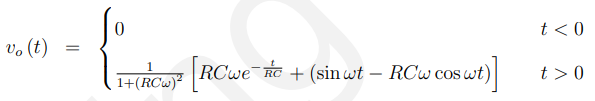
注意当t趋近无穷时,上面的解变为:
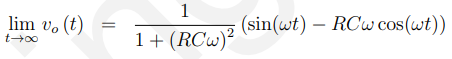
11.2 双边Z-变换((Two-sided) z-transform)
首先我们会给出定义然后我们会证明这确实是采样信号的拉普拉斯变换的定义是:
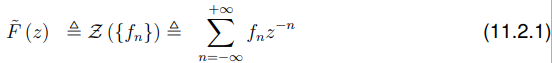
假设脉冲采样信号:
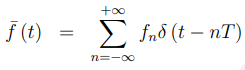
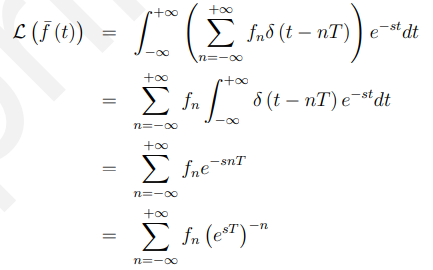
让,可得
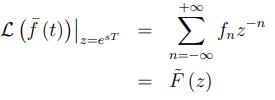
我们已经证明了离散信号[fn]的(双侧)z变换等于脉冲采样信号f (t)的(双侧)拉普拉斯变换,只是符号变化很小,为
11.2.2 序列变成多项式(Sequence becomes a polynomial)
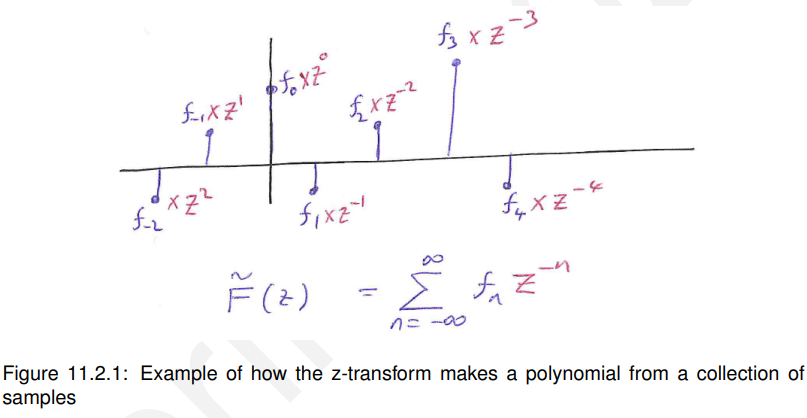
z变换将一个序列[fn)(即样本的集合)变成一个多项式,方法是将的唯一次方加到每个样本上,并将所有项加到一起,见图11.2.1。
11.3.1 指数衰减练习(11.3.1 Exponential decay exercise)
![]()
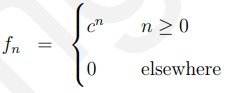
Z变换为:
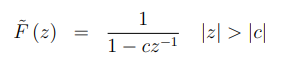
过程:
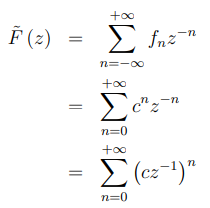
当且仅当 ![]()
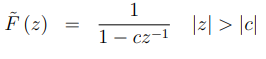
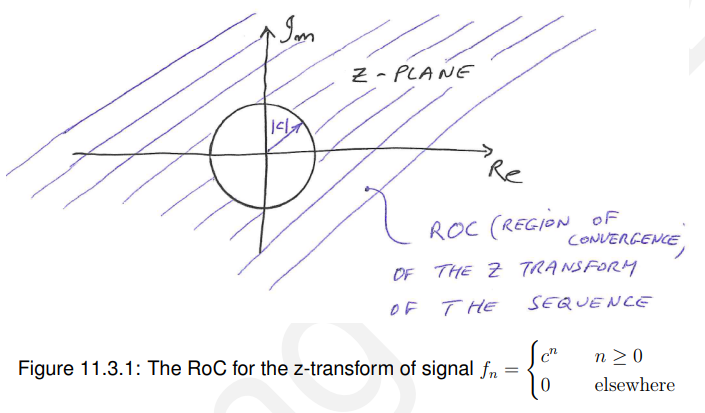
11.3.2 其他形式的Z变换(非常非常重要)
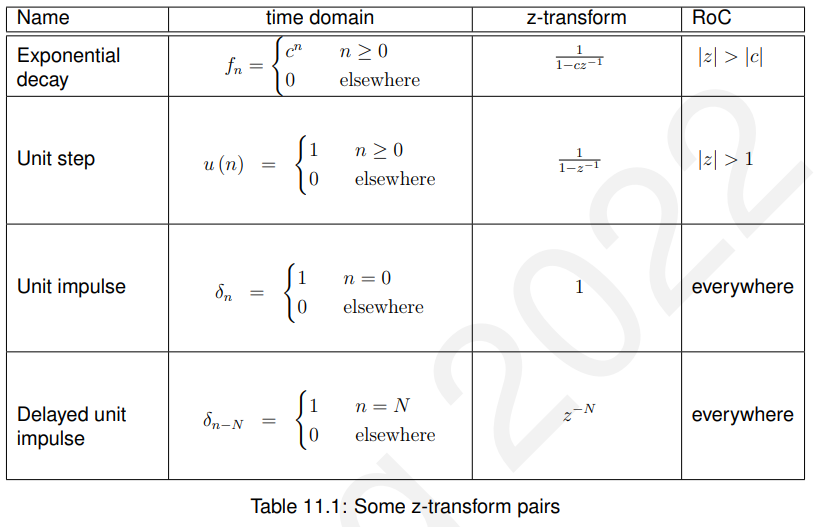
证明过程:


11.4 Z变换的性质(Properties of the z-transform)
11.4.1 linear
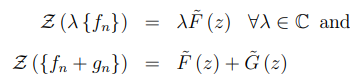
证明过程:
考虑第一条准则:
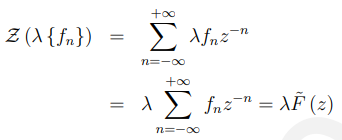
考虑第二条准则:
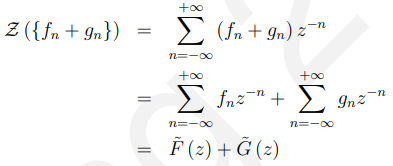
所以这两条都是对的,为了更方便计算,我们使用一下公式表示:
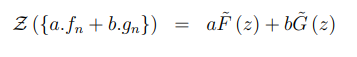
11.4.2 Shift
![]()
证明过程:
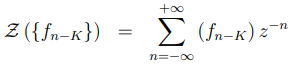
让
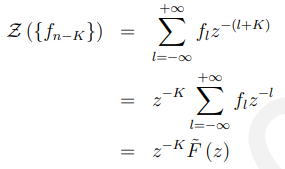
正因为上述定理,经常被称为延迟算子,即每次你想延迟一个信号的一个样本时,只需乘以
;事实上,在DSP世界中,我们经常表示如图11.4.1所示的信号延迟线
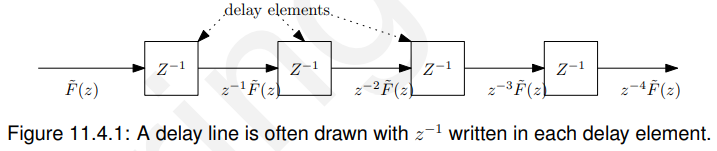
11.4.3 与DTFT的关系
它的重要性在于,一旦我们知道了z变换,我们就可以很容易地计算DTFT。我们还注意到,可以通过让来计算DC (w = 0)响应,可以通过让
来计算
点的响应,这些以及其他一些在图11.4.2中显示。
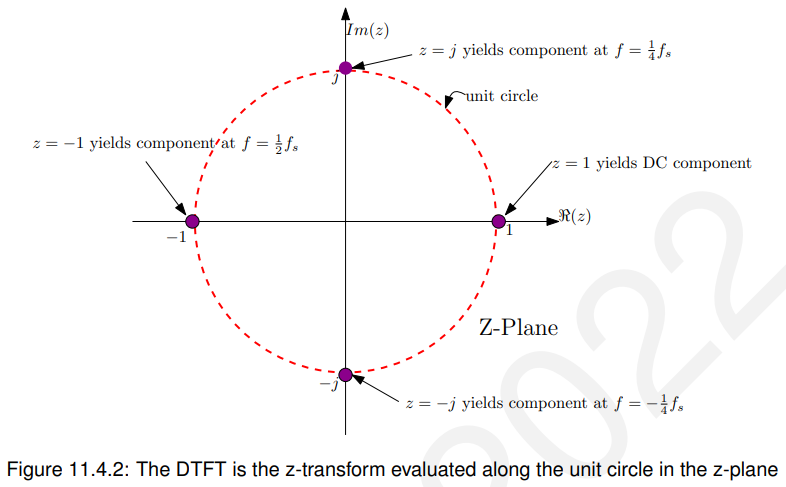
11.4.4 卷积(Convolution)
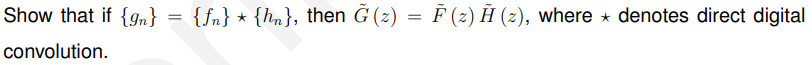
卷积变点乘(这个很nb)
证明:
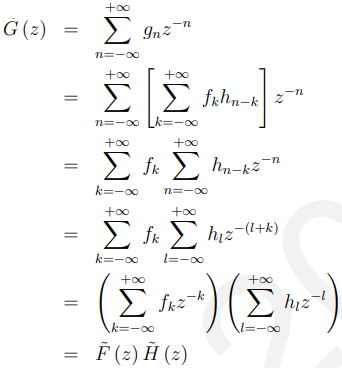
二元性(Duality): 我们又看到了通常的对偶性,即一个域中的卷积对应于另一个域中的乘法。
11.5 Z逆变换
• z逆变换的形式如下(无需证明):
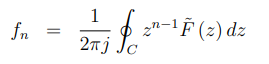
式中,C为z平面上在收敛区域(RoC)内围绕原点的任何逆时针闭合轮廓线。
我们很少用这种形式的z逆变换。对于几乎所有的实际情况,通常都有更简单的技术可以应用。
第12章:Introduction to Digital Filtering
12.1 背景介绍
数字滤波器可以用来过滤模拟信号,只要提供一种机制来采样输入,并重构输出,如图12.1.1所示。

数字滤波器可以被设计成做各种各样的事情,例如,它可以被用来平滑一个有噪声的信号通过去除高频成分一个低通滤波器。图12.1.2展示了这样一个过滤器的运行示例。
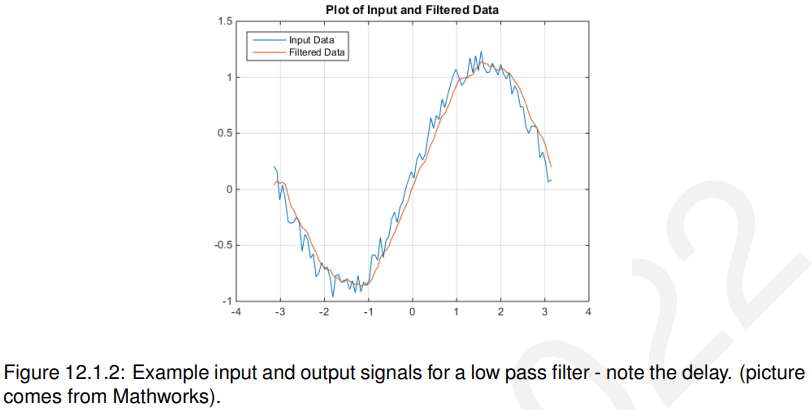
在本章中,我们将研究描述数字滤波器输入和输出之间时域关系的一般方程。然后我们将研究它的一些性质,并考虑它的z域表示。这将为后面课程中更高级的滤波器设计和分析提供良好的基础。
12.2 数字滤波器方程(Digital filter equation)
一个大类的线性、时不变、单输入单输出(SISO)的离散时间系统可以用方程来描述:
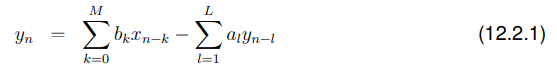
这是一个差分方程,是数字滤波的基础。
[an]和[bn]的值(有时称为系数)是常数,即系统是时不变的。
[xn]是输入,[yn]为输出,即滤波后的信号。
图12.2.1中显示了实现这种过滤器的一种明显的方法。
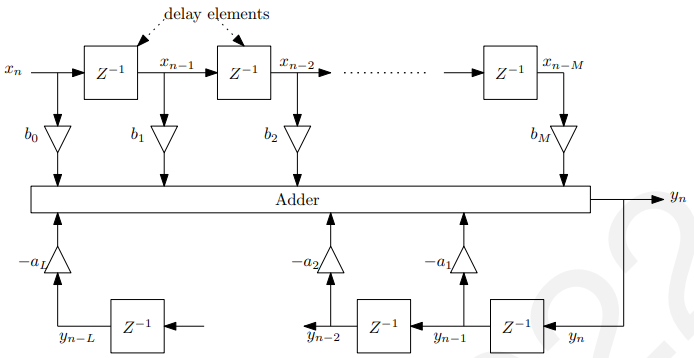
通过调整[a]和[b]系数,可以改变过滤器以执行不同类型的过滤操作。这种能力显然提供了巨大的灵活性,使一个硬件或软件可以很容易地重新配置,以适应许多任务,这也是为什么数字信号处理在今天如此广泛的原因之一。
12.2.1 Linear
证明12.2.1的等式是线性的:
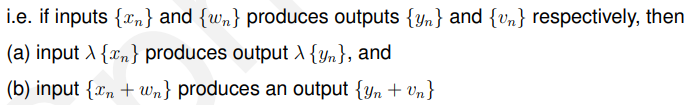
证明过程:
先证明(a):
首先假设,当输入是时,输出实际上是
,看看我们是否得到矛盾:
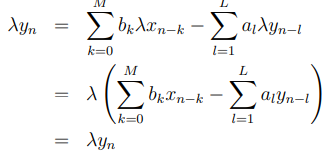
得出结果是对的
再证明(b):
采用相同的方法,假设当输入是时,输出是
,即:

由于线性要求(a)和(b)都被满足,证明是完整的。
12.2.2 时不变(Time invariant)
表明方程12.2.1的z变换是时不变的。
![]()
证明过程:
和前两个证明一样,假设输入为,那么输出为
,即:
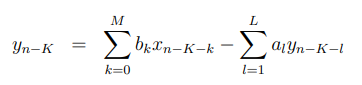
让 ,
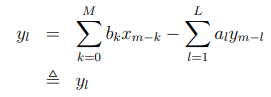
12.3 传递函数(Transfer function)
就像在连续时间系统中用拉普拉斯变换来得到系统的传递函数一样,这里我们用z变换。如果
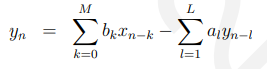
然后我们定义传递函数为:

允许我们将输入/输出关系简单地写为:
![]()
练习:

证明过程:
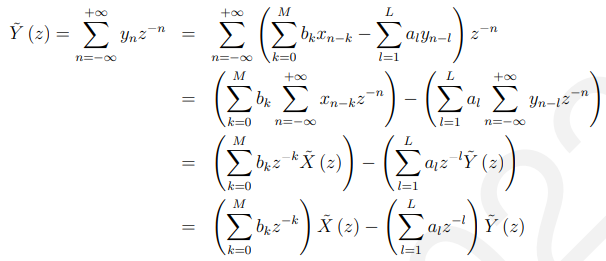
可得:
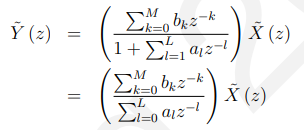
最后一行是通过![]() (没有失去一般性)定义到达的。
(没有失去一般性)定义到达的。
但分子是[bk]的z变换,而分母的和是[ak]的z变换,因此有:
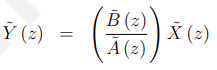
由此可得:
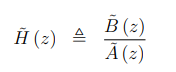
12.3.1 多项式的系数(Ratio of polynomials)
我们可以把传递函数写在“long-hand”上:
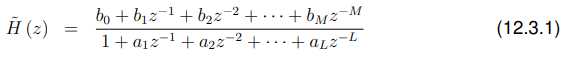
也就是说,这是两个多项式的比,分子B (z)和分母A (z)
12.3.2 极点和零点 (Poles and zeros)
H (z)的极点和零点的定义为:
零点: 在z平面上 H (z) = 0 的点。
极点: z平面上 H (z) 除以0的点(即它会爆炸到无穷)。
注意,根据定义,B (z)只包含z的负次幂,因此我们可以这样分解:
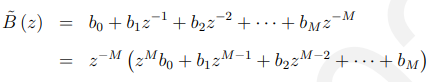
即起始项和
的正幂多项式。从这种形式,我们现在可以在z平面的根集合中再次分解它:
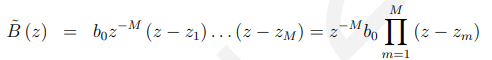
其中是平面(不是
plane)中B (z) = 0的位置,即
的零。我们还注意到在z = 0位置B (z)有m个极点。
分母也是这样:
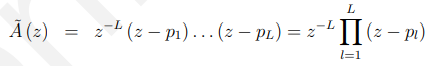
(注意,上面没有显示)。
结合这些我们有:
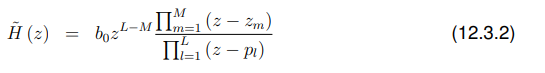
我们看到,在z = 0处,如果L >m有L - M个零,如果M > L有M - L极点。
假设H (z)是不可约的,我们可以说除了x = 0处的极点或零,还有M个零点和L个极点。
你应该很容易就能验证这一点:
•如果(对于任意m),则分子为0,因此
。
同样地,对于任意,如果
那么分母为0我们有一个除以0的情况通常得到
12.3.2.1 零极点图(Pole-zero diagram)(重点!!!)
滤波器的极点和零点的位置对频率响应和稳定性都有巨大的影响,它是许多数字滤波器分析和合成的基础。
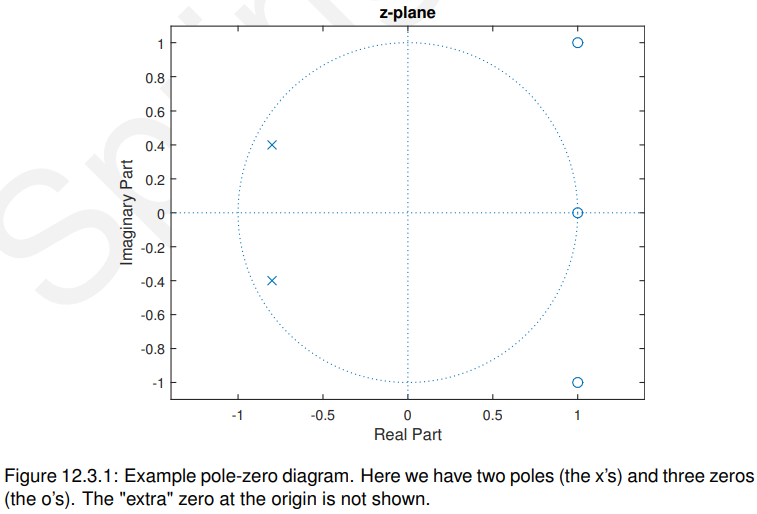
我们通常喜欢在极零图上可视化它们,如图12.3.1所示。符号:
.“O”用来表示零,即H (z) = 0
.“X”是用来表示极点的。
为了清晰起见,我们通常不会在原点画极点或零点,因为
a)它们总是存在于因果滤波器中,只会混淆问题,
b)可以证明它们不影响幅度响应或稳定性(然而,它们通过添加或减去一个固定的群延迟来影响相位响应——请参阅z变换的移位特性)。
12.3.3 实系数多项式(Polynomials with Real coefficients)
表明,如果任何多项式的系数是实数,那么根要么是实数或者它们以共轭对的形式出现。
设![]() 为任意n阶实值系数(ak)多项式。这里的主张是,如果
为任意n阶实值系数(ak)多项式。这里的主张是,如果是根,那么
也必须是,所以我们假设
是f (x)的根,即假设:
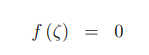
则:
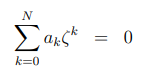
![]() 为:
为:
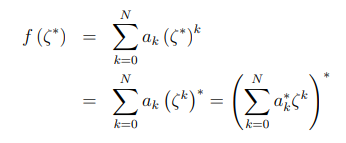
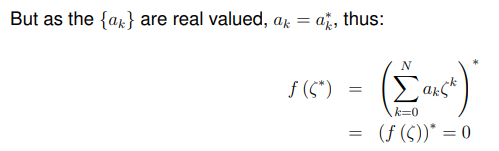
得到定理:如果任何多项式的系数是实的,那么根要么是实的,要么是共轭的。
12.3.4 实系数滤波器 (Filters with real coefficients)
设数字滤波器的传递函数为两个多项式之比,两个多项式的系数即为滤波器系数本身,即:
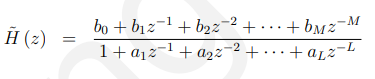
我们可以应用上述定理,并声明:
如果滤波器系数都是实值,那么极点和零必须是实值或出现在共轭对中。
这在图12.3.1中得到了说明,其中有两个极点以共轭对的形式出现(在), 3个零由1个实值零(在x = 1)和2个其他的以共轭对的形式出现(在
)组成。因此我们可以肯定地说,这个过滤器的系数都是实值的。
12.4 频率响应(Frequency Response)
12.4.1 模拟信号的数字滤波(Digital filtering of an analog signal)
正如本章引言中提到的,可以使用数字滤波器对模拟信号进行滤波。
当然我们想知道模拟传递函数H (jw)和数字传递函数之间的关系。
通过查看图12.4.1,我们可以图形化地推导出这种关系。
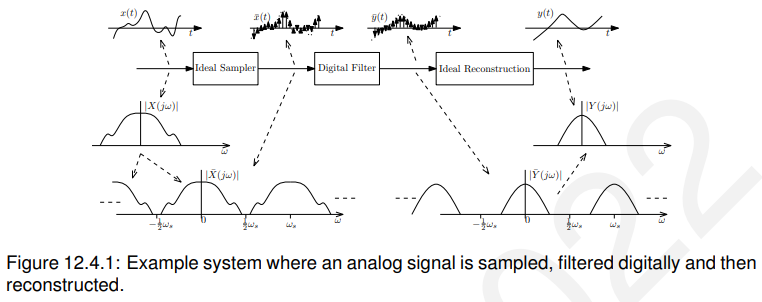
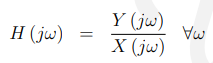
在![]() 的区间中:
的区间中:
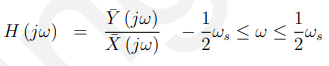
让![]()
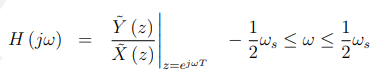
或者更紧凑一点,我们有:
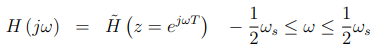
根据上面的讨论,当我们讨论离散系统的频率响应时,我们指的是,不管是否有模拟信号!
12.4.2 周期(Periodic)
概述:频率响应现在定义为:
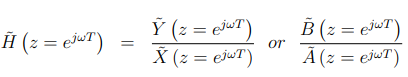
两个dft的比值,每个dft都是周期性的,因此频率响应也是周期性的,如图12.4.2所示。
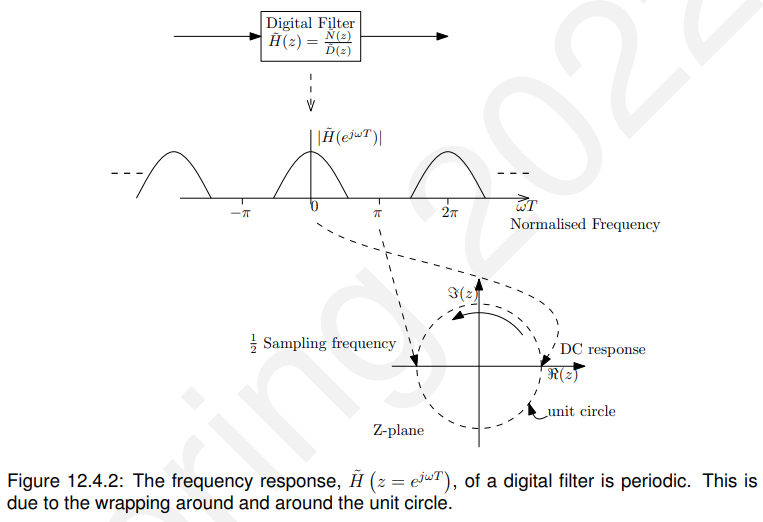
第13-15章:Finite Impulse Response(FIR)filter
13.1 基本定义(Basic definition)
有限脉冲响应(FIR)滤波器,也称为非递归滤波器,几乎用于每一个DSP应用。如果我们让等式12.2.1中的所有[ak]系数为零,我们得到:

即电流输出yn是电流和M最近输入'的加权和,如图13.1.1所示。
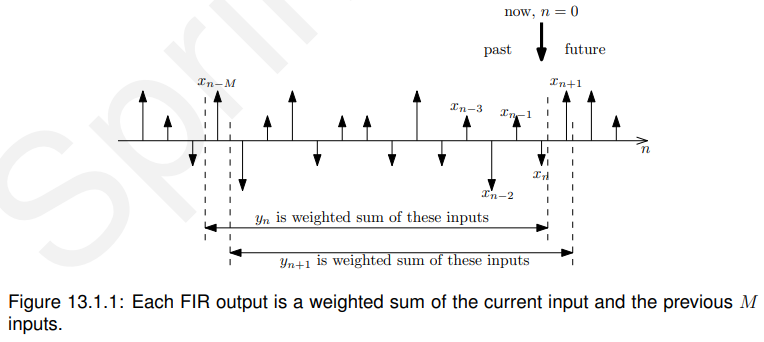
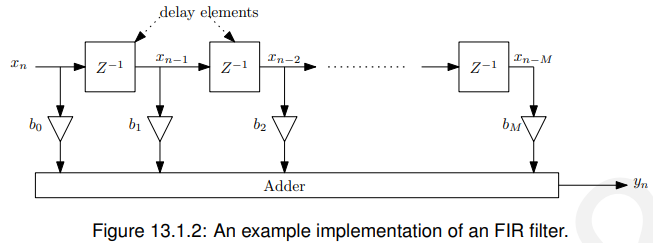
公式13.1.1可以使用如图13.1.2所示的结构来实现。
13.2 特性(Properties)
13.2.1 冲激响应(Impulse response)
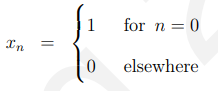
简单地看一下图13.1.2,沿着延迟线沿着“1”计算输出,你应该能够创建以下表格:

所以输出就是系数[bk]:
![]()
注意:这个输出在持续时间上是有限的,即当和
时
,因此称为有限脉冲响应(FIR)滤波器。
13.2.2 阶跃响应(Unit step response)
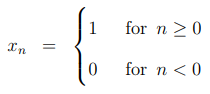
再次简单地看一下图13.1.2,沿着延迟线沿着“1”计算输出,你应该能够创建以下表格:

单位阶跃输入的稳态条件也是系统的直流响应,即。如果你一直代入1你得到的输出总是等于系数的和。

13.2.3 转换方程(Transfer function)
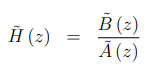
但在FIR滤波器的情况下,除总是被定义为= 1外,[ak]系数都为零,因此A (z) = 1,因此:
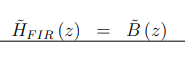
13.2.4 零极点(Poles and zeros)
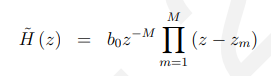
也就是说,原点有M个极点,M个零。
13.3 示例:丝锥过滤器(two tap filter)
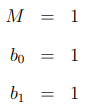
图如13.3.1所示:
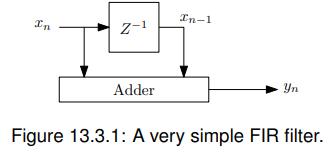
输出为:
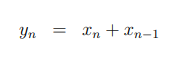
13.3.1 冲激响应(Impulse response)
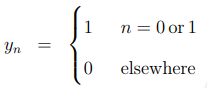
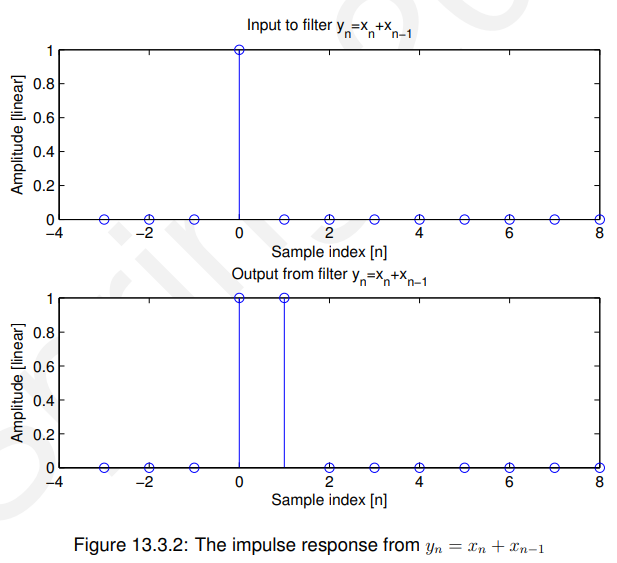
13.3.2 阶跃响应(Unit step)

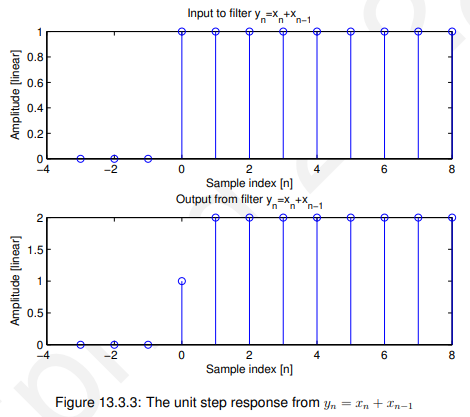
13.3.3 对正弦波@1/4fs的响应(sine wave)
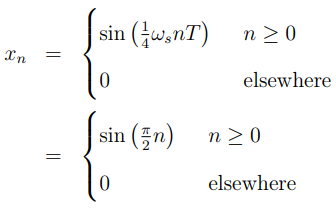
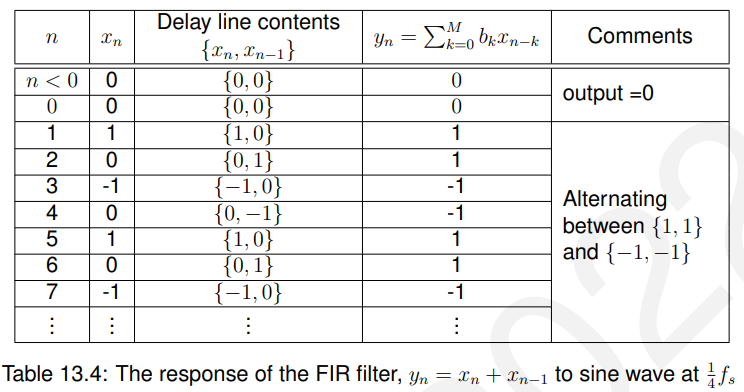
振幅和相位可以计算,当n = 2时其振幅为1,当n = 3时为-1,即:
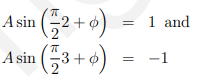
通过等式左边的两个等式来解:
![]()
两个角都减去
![]()
注意sin是一个奇函数,最小的角是。
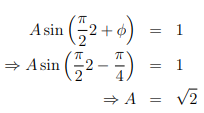
所以最终输出为:
![]()
图像如下所示:
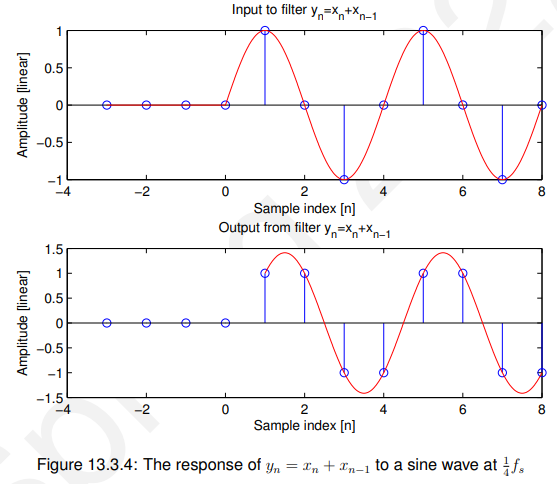
13.3.4 对余弦波@ 1/2fs的响应(cosine wave)

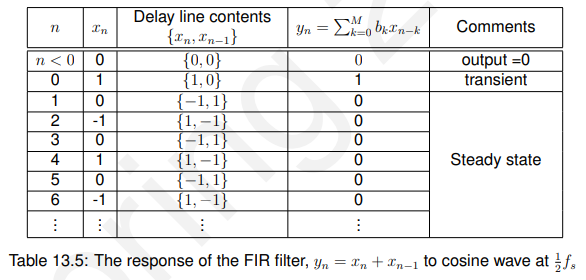
所以在稳定状态下(即当n > 1)输出总是零!!! 如图13.3.5所示:
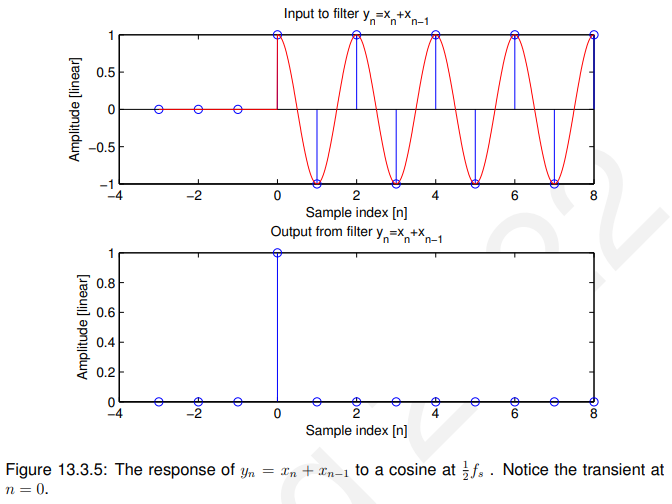
13.3.5 传递函数(Transfer function)
对于FIR滤波器传递函数就是系数的傅里叶变换在这种情况下是[1,1]所以我们有
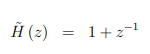
通过计算处的传递函数得到频率响应,即:
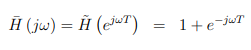
示例:
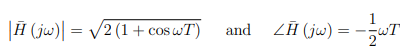
证明过程:
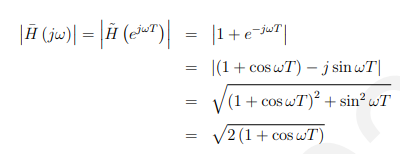
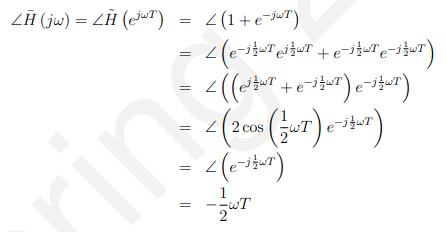
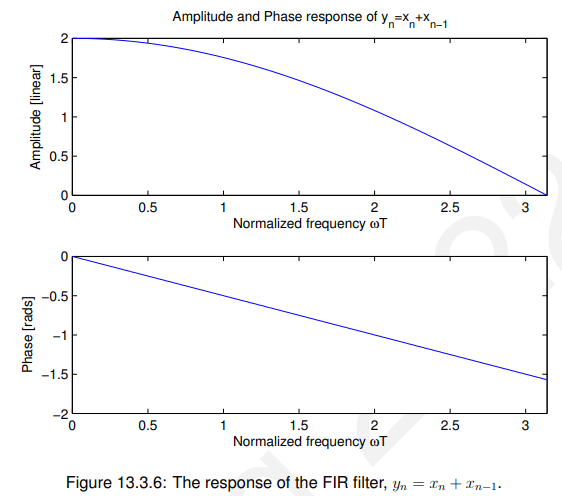
相位响应是线性的(关于w)这是一个非常重要的结果。线性相位响应意味着每个频率分量被延迟一个固定的量(由相位响应的斜率给出)。这种固定延迟特性在许多音频和视频信号处理中都是非常重要的。
13.3.6 简单方法
在前面的小节中,我们计算了各种输入类型的输出。如果我们只对稳态行为感兴趣,那么我们可以简单地使用传递函数H (z)如第13.3.5节所计算。
这在表13.6中显示,可以看到这与先前导出的结果一致。

14.1 为什么需要线性?
想象一个模拟滤波器,它以相同的延迟通过特定输入信号的所有频率成分,例如以秒为单位增益。那么几个频率的输入输出可以如下表所示:
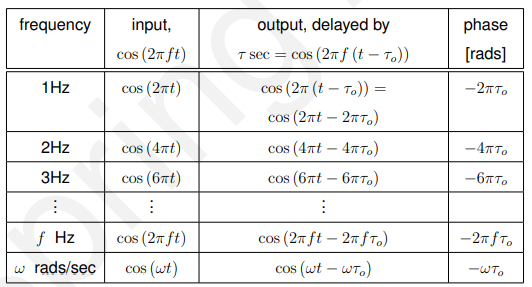
即如果一个滤波器的相位响应是w的线性函数,即![]() 则该滤波器的群延时为to秒,因为所有频率分量的群延时为
则该滤波器的群延时为to秒,因为所有频率分量的群延时为秒。
如果一个信号的所有频率成分都在理想滤波器的通带内,那么除了一个固定的延迟或秒外,它既不会发生振幅失真,也不会发生相位失真。这就是为什么我们几乎总是尝试设计线性相位滤波器。
作为一个例子,图14.1.1显示了低通滤波器的理想响应。
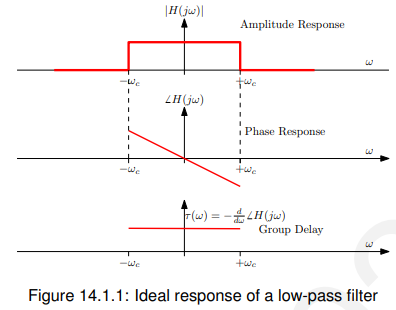
14.1.1 群时延(Group delay)
更正式地,我们将滤波器的群延迟定义为减去相位响应的导数:
![]()
显然,在上面给出的例子中,滤波器引入了一个固定的时间延迟。如果,我们有
which有意义,如图14.1.1所示。题外话:技术上,
,也被认为是线性相位,但一个非零常数K违反了我们经常想要的良好延迟特性,但尽管如此,这些类型的滤波器确实找到了相同的应用,例如在微分器和希尔伯特变压器(超出了本课程的范围)。
对于离散时间滤波器也可以采用相同的参数,所以现在我们将考虑需要什么条件来确保实值滤波器的线性相位响应。
14.2 实滤波器的充分条件(Sufficient conditions for real filters)
我们希望找出实值FIR滤波器具有精确线性相位响应的条件。由第13.2.3节可知,系数为[bk]的FIR滤波器的传递函数H (z)为:
![]()
其中B (z)为系数的z变换。扩展一下,我们有:
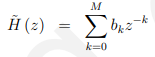
总共有M + 1个系数。
我们再次强调(目前)我们将假设[bk]都是实值。
14.2.1 预备(Preliminaries)
我碰巧知道结果的群延迟是y,所以作为起点,我们重写传递函数H (z),通过提出延迟,我们从位移定理知道,它涉及到z的幂次乘法,即:
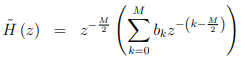
我们感兴趣的频率响应角H (jw)由沿单位圆计算H (z)得到,即当'时,有:
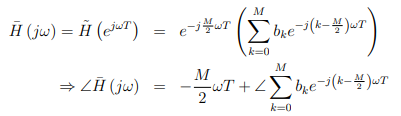
如果上面的和角是w的线性函数,这就是线性相位。
即我们需要选择[bk]来保证![]() 是w的线性函数。
是w的线性函数。
14.2.2 对称(symmetry)
如果实值系数具有对称性,即或反对称
,则得到的滤波器将具有线性相位。更一般地,我们可以把
或
写成
。
为了证明这一点,我们需要考虑系数为奇数和偶数的两种情况,并分别考察和
时
的相位响应。
14.2.2.1 偶数个系数(An even numbe of coefficients)
如果M为奇数。![]() 可以分成两等份:
可以分成两等份:
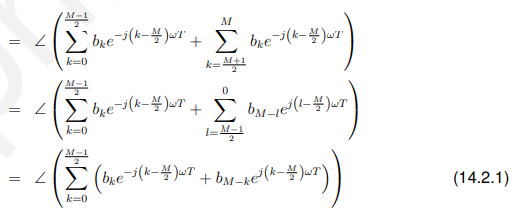
在上面的第二行中,我们用来使两个和的范围相同。
在第三行,我们合并两个和。
现在我们应用的假设
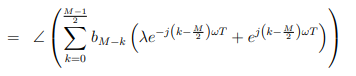
注意,这两个指数互为复共轭,对于任意复数v,![]() 和
和![]() ,因此:
,因此:
•如果λ = 1(即对称情况),上面括起来的项是实值。
•如果λ= -1(即反对称情况),上面括号中的项是复值。
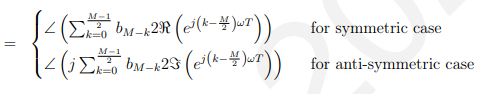
对于对称情况,一切都是实值phase = 0 or = 。
对于反对称情况,一切都是phase = 。
最后我们有:
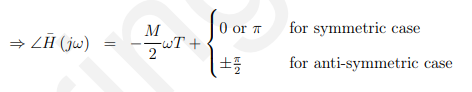
它们都是w的线性函数。
因此,对称系数或反对对称系数是偶数系数FIR具有线性相位响应的充分条件。
在这两种情况下,群延迟都是秒(这是两个中间系数的中间位置)。
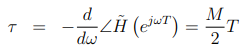
作为一个例子,图14.2.1显示了长度为10的FIR滤波器的这种情况。
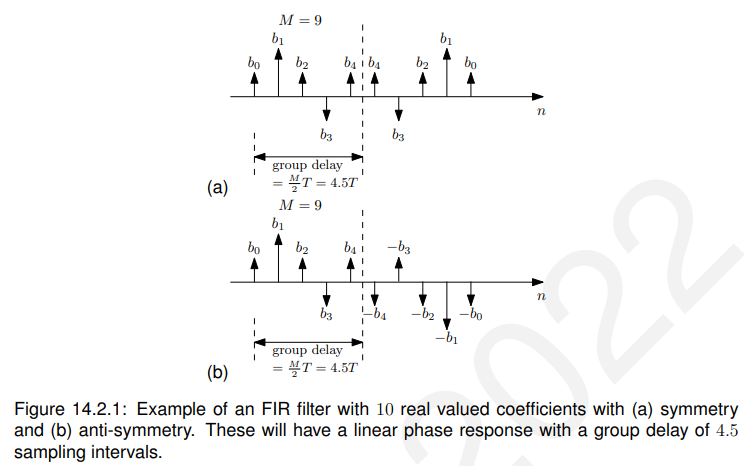
注意:对于奇数和偶数情况,有两个方程的相位响应,每一个正好有弧度的不同。这对应于信号反转,即FIR滤波器有正增益和负增益的情况;记住响应的大小(根据定义)是正的,所以信号反转必须体现在相位响应中。
14.2.2.2 奇数个系数(An odd numbe of coefficients)
规则也适用于奇数系数,这是很容易证明的,完全相同的方式上,除了我们必须考虑中间系数
:
如果,那么中间项
可以有任何值
如果,那么中间项
必须= 0,因为这是唯一的方法,假设是实数。
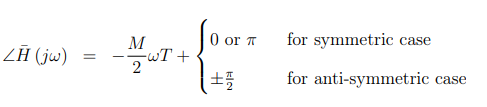
群延迟(这是中间系数的位置)。
作为示例,图14.2.2显示了长度为11的FIR滤波器的这些条件。
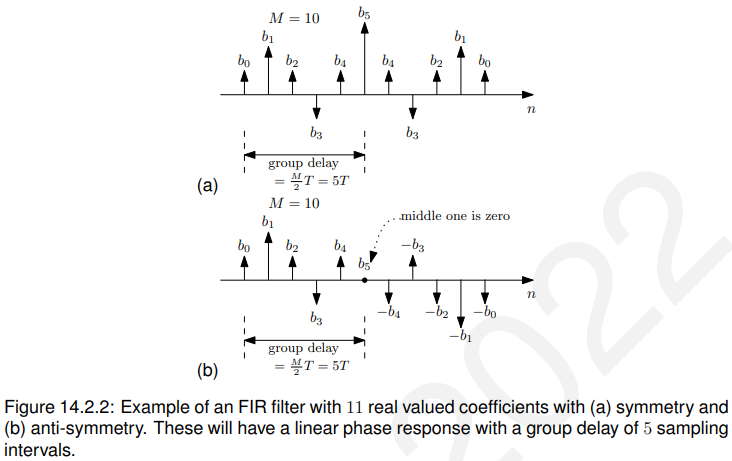
14.2.3 结论(Conclusion)(究极重要!!!!)
实值线性相位FIR滤波器可以通过保证系数具有以下任一项来构造:
1. 对称:![]()
2. 反对称性:![]()
如果有一个奇数的系数,并且有一个中间的系数,必须为= 0反对称性。为了对称,中间系数是不受约束的。在所有情况下,组延迟为:
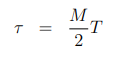
我们现在声称,无需证明,对于实值FIR滤波器,这些表示线性相位的必要条件,即它们不仅仅是充分的。
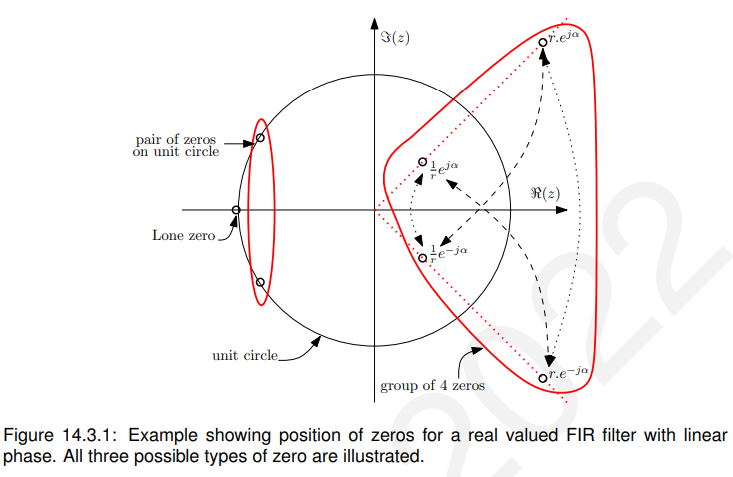
14.3 z域中视图
请注意,我们已经在第12.3.4节中建立了任何具有实系数的滤波器,其极点和零要么在z平面的实轴上,要么在共轭对中。
FIR滤波器只有零,但仍然符合以下规则:实值FIR滤波器有实零和/或它们以共轭对出现。
在原点也有M个极点。线性相位滤波器对零点的位置有一个额外的约束,我们现在将看到。
练习:
除了上面的标准,实值线性相位FIR滤波器的零以反相对出现,即对于线性相位滤波器,如果是零,那么
也是零。
证明过程:
若是零:
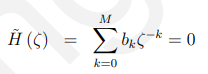
但是线性相位滤波器的系数是对称的,(我们将在证明的最后处理反对称的情况),因此:
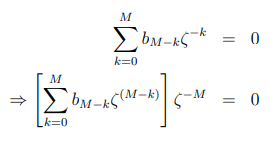
让 :
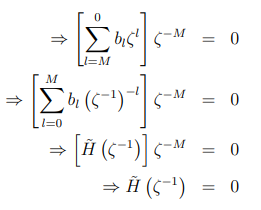
最后一行暗示确实是一个根。注意,如果我们假设反对称,即
,那么我们就会得到这样的结论:
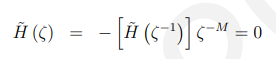
也能证明确实是一个根。
结论:
所有实值线性相位FIR滤波器要么是实值零,要么是共轭出现,另外任何零的逆也是零。
基于以上结论得出:
在z = -1或z = +1时(因为+1是唯一的实数值,是它们自己的逆)。
在单位圆上的共轭对。.
一组4个,例如![]() 和它的逆
和它的逆![]() 。
。![]() 以及它们的共轭词
以及它们的共轭词![]() 。
。
第15章:FIR滤波器设计
15.2 傅里叶系数法(Fourier series)
提示:周期函数f (t)可以用傅立叶级数表示:
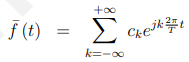
式中T为f (T)的周期。傅里叶系数c的计算公式为:
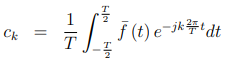
FIR设计应用:
任何数字滤波器的频率响应H (jw)都是周期性的,也可以用傅里叶级数表示(注意,通常我们说时域信号是周期性的,用傅里叶级数表示,而这里我们互换了时间和频率的角色)。图15.2.1说明了这一点。
注意,周期(通常表示为T)实际上是.
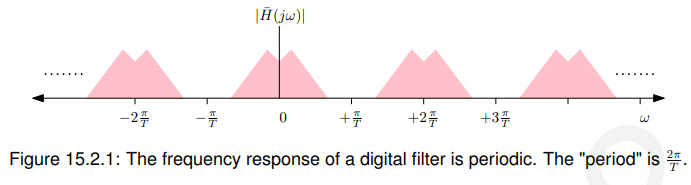
因此,将傅里叶级数应用于H (jw)(时间和频率的作用颠倒’),我们得到:
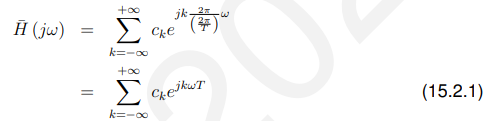
其中:
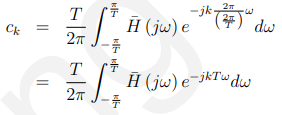
但是一个(无限)长且系数为{bk} 的FIR的频率响应为:
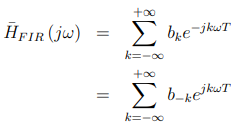
我们可以得出:
![]()
那么得到的FIR将与期望的H (jw)具有相同的频率响应。但是我们有一个傅立叶系数[ck]的方程,因此:
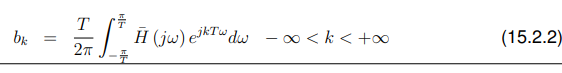
这就是所谓的滤波器合成公式。
现在我们将看一些例子,并了解这种方法的一些局限性。
15.2.1 线性相位LPF
我们需要一个响应如图15.2.2所示的过滤器,并在数学上用描述(记住它在该范围外是周期性的):
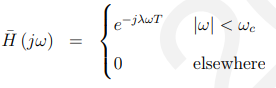
其中与群延迟有关,可以是任意实数>0。
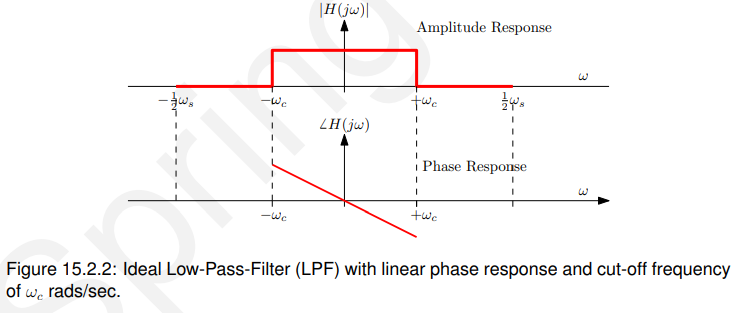
通过式子15.2.2,可得:
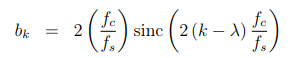
其中![]()
证明过程:

例如:![]() (对应于零相位滤波器),
(对应于零相位滤波器),
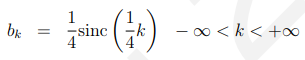
中间的21个值(大约k = 0)如图15.2.3所示。
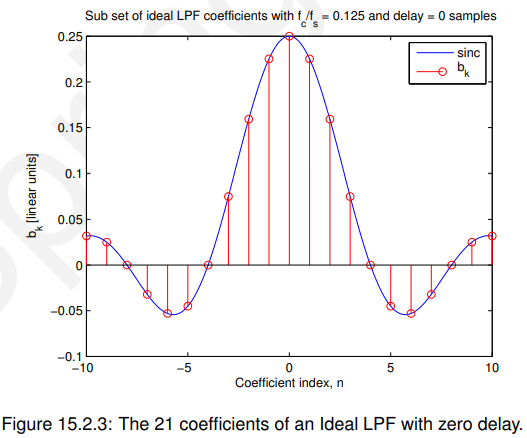
15.2.2 有限长度
filter synthesis formula(15.2.2)的一个问题是,它产生了无限数量的系数[bk],显然不能在有限的机器中实现!
我们可以简单地取其中的一个子集,例如中间的21个系数,如图15.2.3所示。通过这样做,我们将期望过滤器的响应将不再与精确的规范匹配,而是一个近似值—如图15.2.4所示。
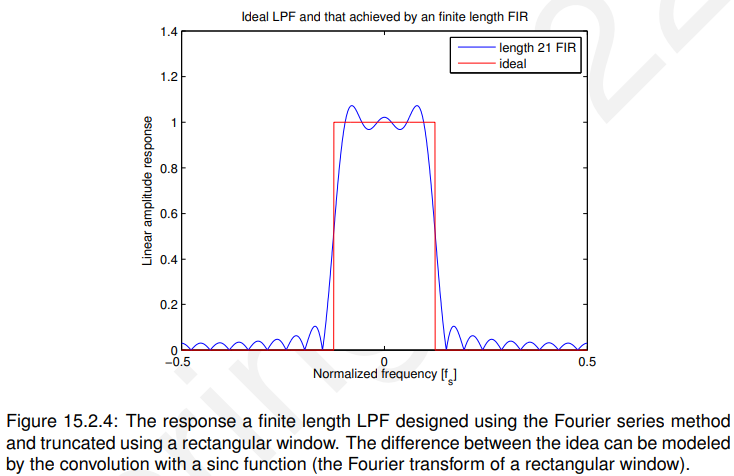
取系数的一个子集的过程可以用数学模型表示为(采样的时域)滤波器系数与矩形窗口(在本例中为21)的乘积。
使用通常的傅里叶对,我们可以说,对频率响应的影响是与矩形窗的傅里叶变换的卷积,即另一个sinc函数。如图15.2.3所示,该卷积具有涂抹理想响应的效果。
和很多傅里叶变换一样,时域矩形窗越宽(即。我们取的样本越多,sinc形状的频域越窄,即卷积的影响越小。
关于窗口的主题需要进一步探讨,我们将在15.3节中讨论。
15.2.3 因果关系
图15.2.3中呈现的系数集合的另一个问题是它们是非因果关系,即它们不会从k = 0开始,所以任何实现都需要时间机器!
然而,这很容易通过简单地引入延迟来解决。
回顾第14节中关于线性相位滤波器的讨论。
所设计的滤波器具有群时延为的线性相位响应:
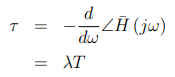
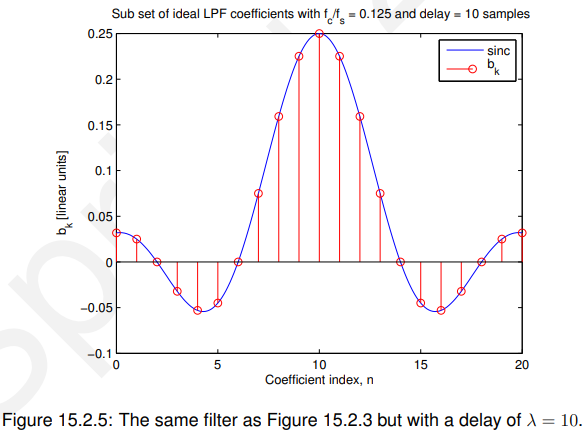
这就是为什么在图15.2.3中设置会产生一组以k = 0为中心的系数。例如,如果我们选择
,我们将得到一组如图15.2.5所示的系数——这是因果关系。
15.3 窗函数法(Windowing)
为了演示加窗的原因,我们首先考虑第15.2.1节的例子,给出了一个21系数的设计——现在我们在图15.3.1中展示了其对数尺度上的振幅响应,以及其他几个长度(按照相同的程序获得)。
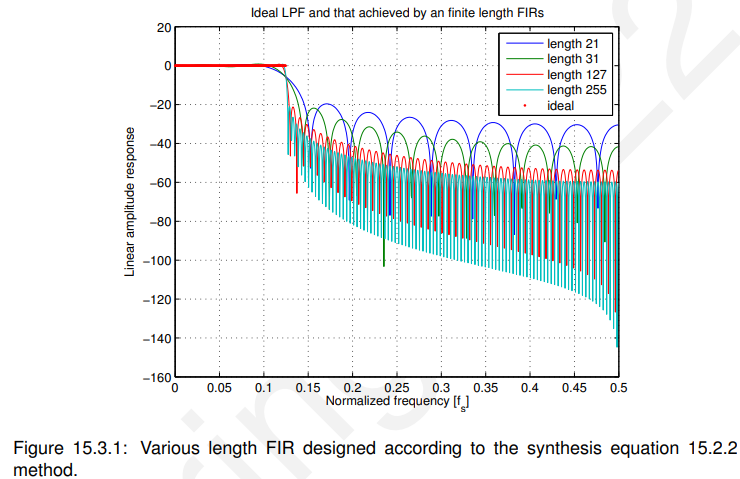
由下表可以看出,随着长度的增加,阻带衰减缓慢增加:
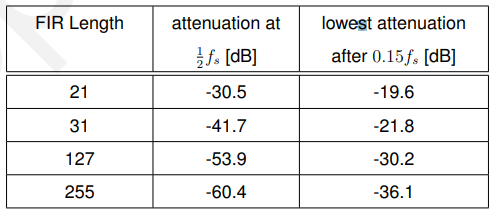
因此,我们得到近20dB的阻带衰减与长度21滤波器,但只有额外的10dB改善,当实现127长度衰减的缓慢增加是主要原因这也是矩形窗不受欢迎的主要原因之一。
要查看在通带内发生了什么,我们需要按图15.3.2放大。在这里,我们看到在通带内的峰值误差仍然很大-特别是接近过渡带的开始。这被称为吉布斯效应-只有当我们取完整的(无限数量)系数集将不会有这个误差。
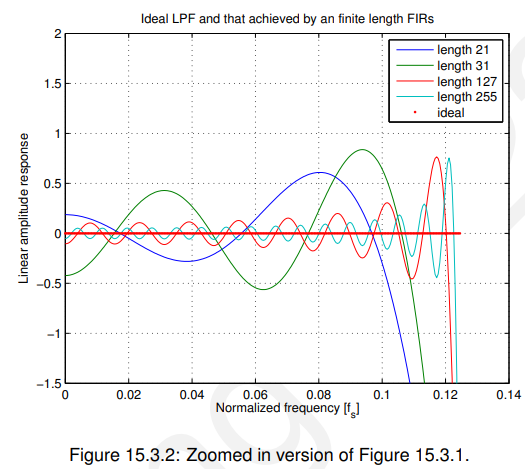
15.3.1 数学模型(Math model)
我们可以模拟从15.2.2滤波器设计公式中取有限数量的样本作为一个矩形时域窗口的乘法。在频域中这样做的结果是通过傅里叶变换进行卷积。图15.3.3说明了这一点。
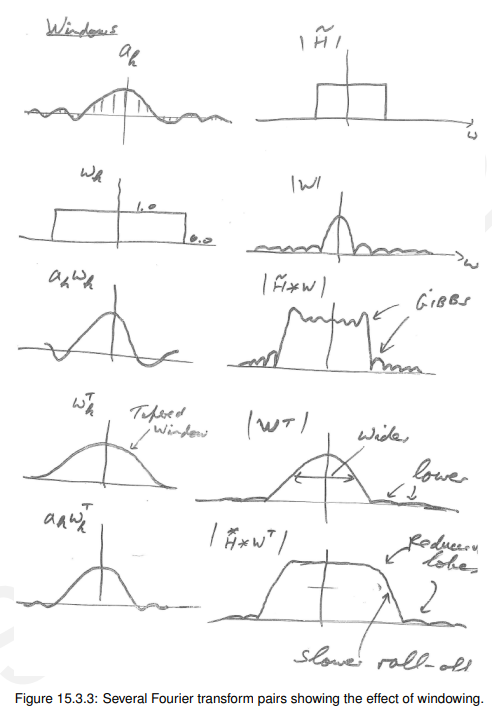
图15.3.3中还显示了使用锥形窗口。在频域上,它的主瓣更宽,但旁瓣更小。因此,它将得到的振幅谱进行了不同的扩展:
过渡带变慢,但是
阻带中的侧叶可以低得多。
15.3.2 窗口类型(Windowing procedure)
当截断无限集[be]时,执行以下操作:
将窗口置于能量最大区域的中心(中间系数).
在这个中心点取等量的样本-这保证了系数的对称性,从而保持了线性相位。
乘以窗函数[wk],它被假设在有限的系数以外为零,也就是说,当k = 0时,滤波系数变为对于k= 0 ,…,M.
一般窗函数:
• Rectangular
• Hamming(*)
• Blackman
• Kaiser(*)
举个例子,我们来看看广受欢迎的汉明窗和凯撒窗。
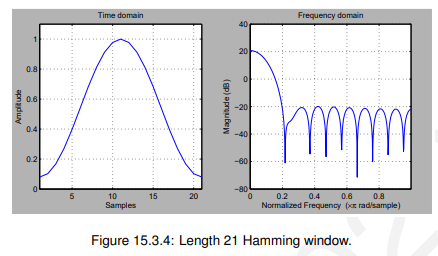
15.3.2.1 汉明窗(Hamming)
汉明窗本质上是一个凸起的余弦形状:
![]()
注意,它的峰值(值= 1.0)出现在中间位置。图15.3.4显示了一个示例:
15.3.2.2 凯撒窗(Kaiser)
Kaiser窗口的定义如下:
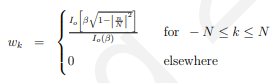
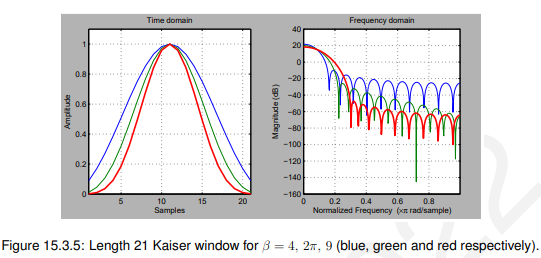
式中,β为控制旁瓣电平的窗口参数,为修改后的第一类零阶贝塞尔函数,计算公式为:
![]()
在实践中,无穷和被一个足够大的和所取代,以产生所需的精度水平。“β的范围是任何正实数,用于控制旁瓣的水平。β的值越大表示旁瓣越小,反之亦然。这可以在图15.3.5中看到。
15.4 极大极小过滤器(minimax filters)
从实值多项式的研究中,我们得到了切比雪夫等振荡定理,现在我们不需要证明就可以说明这个定理:
定理:设是区间[a, b]上的连续实函数。在所有阶
的多项式中,最小化最大误差
![]() (在[a, b]范围内)的多项式g有n+ 2个点
(在[a, b]范围内)的多项式g有n+ 2个点![]() ,使得
,使得![]() 其中
其中![]()
换言之,该定理表明,如果目标实值函数f和某个n次多项式g在某个范围[a, b]上的最大误差为ç。那么误差最小的ç就是那个在![]() 区间[a,b]上振荡的多项式。有计算该多项式的方法。图15.4.1说明了这一点。
区间[a,b]上振荡的多项式。有计算该多项式的方法。图15.4.1说明了这一点。
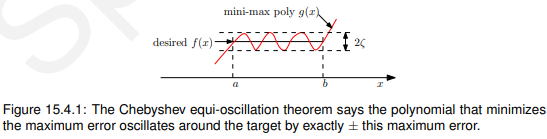
如果我们将目标函数f作为滤波器的期望振幅谱,那么我们可以利用这些方法设计一个n阶多项式g,使期望振幅谱与g之间的最大误差最小化。
此外,我们可以很容易地计算FIR滤波器的系数,以实现任何振幅谱匹配一个有限阶多项式。
结合这些事实,提出了设计FIR滤波器的算法,以使目标规格和某些FIR滤波器响应之间的最大误差最小化。其中最著名的是帕克斯-麦克莱伦算法。
基于这一原理的滤波器被称为极大极小滤波器。
15.4.1 加权区域(Weight regions)
滤波器通常至少有两个区域(在频域),我们对其施加约束,即低通滤波器将有
•允许频率通过的通带
•一个阻止带,我们希望阻止频率成分通过。
承认世界是一个不完美的地方,我们通常会说通带的增益应该“接近于统一”,而阻止带的增益应该“接近于零”。
此外,在通带和阻带之间有一个过渡带,在这个过渡带中我们对滤波器的增益没有任何特殊的限制。
之前概述的minimax FIR滤波器设计过程可以扩展到多个波段,即不仅仅是一个连续的范围[a, b],例如,允许我们指定我们想要同时最小化通带和止带发生的最大误差。
然而,根据应用程序的不同,我们通常更关心某个波段的误差。也就是说,与通带相比,我们可以在阻止带容忍更大的误差。
因此,大多数过滤器设计计算机包允许您为每个感兴趣的波段指定不同的误差权重。
当算法计算期望函数与实际多项式之间的误差时,在进行最小化之前,这些权值用于在不同区域内对误差进行缩放。因此,在程序完成后,权重较大的区域误差较小,即每个区域的加权最大误差在所有区域中应该是相同的。
15.4.2 LPF滤波器示例
考虑一个截止频率为的低通滤波器,并查看来自各种不同权重配置的Matlab@ firpm函数的结果。
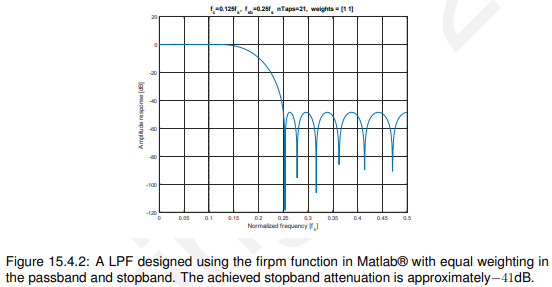
15.4.2.1 相等的权重
将通带和阻带的权重设置为相同,例如[1,1],然后我们对21系数滤波器的响应进行gef,如图15.4.2所示,放大后的版本如图15.4.3所示。

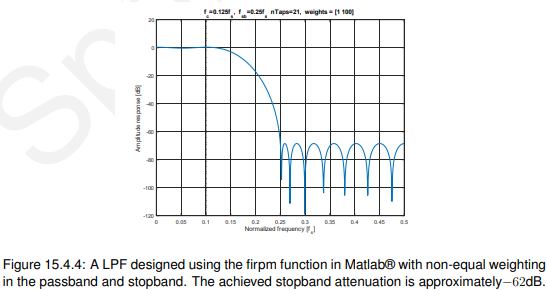
15.4.2.2 不相等的权重
将通带和止带的权值设为[1 100],即止带的最大误差x100应该等于通带的最大误差,也就是说,我们允许的通带误差要比止带大得多。
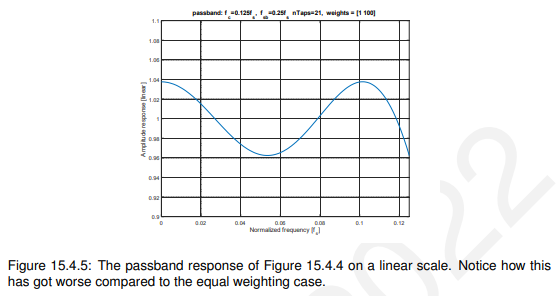
因此,对于相同长度的滤波器,我们期望通带的纹波会增加,阻带的衰减会改善。实际上,如图15.4.4和15.4.5所示。
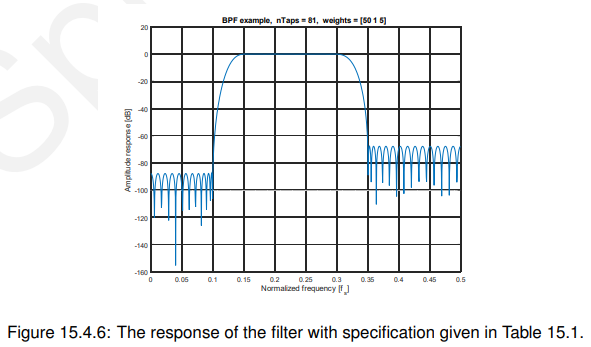
15.4.3 更复杂的示例
考虑一个带通滤波器(BPF),其规格如下:

81系数FIR滤波器得到的振幅谱如图15.4.6所示。


























 1796
1796











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








