LBM（2）——LBM的程序结构

已于 2023-10-30 17:53:49 修改
阅读量1.6k 收藏 28
点赞数 32
文章标签： 算法
于 2023-10-30 12:53:00 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_49472580/article/details/134106585
版权

本文将结合一个验证LBM有效性的最基础算例——poisuille流动，来详细讲解LBM的程序结构。

首先，LBM的程序结构如下：

一.初始化：对于不同的问题，LBM有不同的初始化方法。如定常流动，非定常流动，依赖于时间的周期性流动（如Womersley flow），初始化敏感性流动（如Taylor-Green vortex flow）等，它们具有不同的初始化方法。本文主要介绍最常用的用于定常流动的初始化方法。

定常流动指的是在计算达到稳态时，流体中任何一点的压力，速度和密度等物理量都不随时间变化的流动。LBM在模拟定常流动时进行初始化时，首先将各格子的宏观物理量的值初始化为t=0时的值（通常情况下ρ=1，u=(0,0)），随后令各格子的分布函数等于相应的平衡分布函数的值：

其中，

两式中a与i物理意义相同，均是从0到8的整数，代表D2Q9模型中的9个方向；ω（权重）,e（方向向量）,c均为已知量。由于各格子的速度和密度均初始化为t=0时刻的值，均已知，故格子沿9个方向的平衡分布函数也均可计算得到，所以各格子在初始化阶段分布函数的值均可以确定。

二.LBM主要计算程序

1.计算流体宏观密度和速度：

2.计算平衡分布函数：

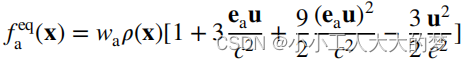
3.执行碰撞步骤：

4.执行迁移步骤：

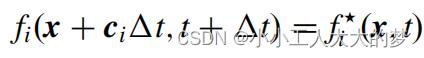
5.边界处理;

6.更新时间步：t=t+Δt，返回第1步。

三.实例分析——平板间的层流流动

首先简要介绍一下poisuille流动的物理背景：

泊肃叶流动（Poiseuille Flow）是一种经典的稳态、不可压缩、层流流体力学现象。这种流动的特点是在一个长直管道内，由于外界施加的压力差，流体在管道内呈现出均匀且平行的流动，流速呈线性分布，流速在横截面上是沿管道半径方向线性变化的。这是一种非常理想化的流动，通常用来解释管道内液体或气体的运动行为。

泊肃叶流动的一般公式如下：

其中：

公式描述了流体速度与距离管道中心的垂直距离之间的关系。泊肃叶流动的速度分布是二次多项式，其最大速度出现在管道中心，速度沿管道半径方向线性减小，最终归于零。这种流动是具有特定几何形状（如圆管）和边界条件的流体的典型行为。

其次，本文选择了江苏大学葛钦钦的硕士毕业论文《基于格子 Boltzmann 理论的流场分析》中基于 LBM 二维管道流型模拟的 MATLAB 代码作为示例进行说明：（文末将附上完整版代码）

clear
close all
clc
tic
% GENERAL FLOW CONSTANTS
lx = 150; % number of cells in x direction
ly = 50; % number of cells in y direction
uMax = 0.1; % maximum velocity of Poiseuille inflow
Re = 100; % Reynolds number
nu = uMax * ly/ Re; % kinematic viscosity
omega = 1. / (3*nu+1./2.); % relaxation parameter
tPlot = 5; % cycles for graphical output
% D2Q9 LATTICE CONSTANTS
% e6 e2 e5
% \ | / 
% e3-e0-e1 
% / | \ 
% e7 e4 e8 
w = [1/9,1/9,1/9,1/9,1/36,1/36,1/36,1/36,4/9];
ex = [ 1, 0, -1, 0, 1, -1, -1, 1, 0];
ey = [ 0, 1, 0, -1, 1, 1, -1, -1, 0];
opp = [ 3, 4, 1, 2, 7, 8, 5, 6, 9];
liq = [2:(ly-1)]; % liquid part
in = 1; % position of inlet
out = lx; % position of outlet
[y,x] = meshgrid(1:ly,1:lx); % get coordinate of matrix indices
obst = ones(lx,ly); 
obst(1:lx,liq) = 0; % top/bottom boundary
bbRegion = find(obst); % boundary is 1 (use bounce back model)

这一部分代码是计算过程中所需参数的定义以及对于参与运算的数组的初始化。最基本的LBM模拟中可以人为控制的参数只有模型尺寸（lx,ly）以及无量纲弛豫时间（τ）。无量纲弛豫时间（τ），雷诺数（Re）以及运动黏度（v）三者之间的关系是“知其一则知其三”，实际参与运算的只有τ，其关系式如下：

其中，Δt=1,格子声速的平方为1/3，运动黏度的量纲也是在格子单位制下的值，而非国际单位制下的值。

整个计算域内的格子被分为两种类型：流体格子以及边界格子。格子类型的信息储存在一个lx*ly的二维矩阵之中，该矩阵是一个其中值非0即1的矩阵，当某一格子的坐标对应边界格子时，该处值为1，否则为0，对应流体格子。这样设置的原因是：在后续计算中，对不同类型的格子需要执行不同的操作，0和1就是用来判断它们类型的“身份证”。

% INITIAL CONDITION
fIn = reshape( w' * ones(1,lx*ly), 9, lx, ly); % reshape all nodes to a new form (9*lx*ly) matrix
fEq=zeros(9,lx,ly); % initial feq is zero
fOut=zeros(9,lx,ly); % initial ftemporary is zero
avu=0; % initial average velocity is zero
prevavu=0; % next node velocity is zero

这一部分代码对所需要用到的分布函数进行了定义和初始化。从本质上来讲，利用LBM进行数值模拟其实就是随着时间步进通过特定的算法更新矩阵：ux(lx*ly),uy(lx*ly),ρ(lx*ly),f(lx*ly*9)的值。这些矩阵包含着计算域内每个格子的所有宏观物理量（速度和密度）和微观物理量（分布函数）的信息。

% MAIN LOOP (TIME CYCLES)
T=0;
while (1e-9<abs((prevavu-avu)/avu)) || T<20000 % give the restriction of circulation
T=T+1 % start to count
% MACROSCOPIC VARIABLES
rho = sum(fIn); % formula of rho
ux = reshape ( (ex * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho; % formula of velocity
uy = reshape ( (ey * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho; % formula of velocity
% MACROSCOPIC (DIRICHLET) BOUNDARY CONDITIONS
ux(:,in,liq) = uMax; % channel inlet x-velocity 
uy(:,in,liq) = 0; % channel inlet y-velocity 
rho(:,in,liq) = 1 ./ (1-ux(:,in,liq)) .*(sum(fIn([9,2,4],in,liq)) + 2*sum(fIn([3,6,7],in,liq)) ); 
% COLLISION STEP
for i=1:9 
cu = 3*(ex(i)*ux+ey(i)*uy); 
fEq(i,:,:) = rho .* w(i) .* ( 1 + cu + 1/2*(cu.*cu) - 3/2*(ux.^2+uy.^2) );
fOut(i,:,:) = fIn(i,:,:) - omega .* (fIn(i,:,:)-fEq(i,:,:));
end
% MICROSCOPIC BOUNDARY CONDITIONS: NO-SLIP WALLS (bounce-back) 
for i=1:9 
fOut(i,bbRegion) = fIn(opp(i),bbRegion); 
end
% STREAMING STEP 
for i=1:9 
fIn(i,:,: ) = circshift(fOut(i,:,: ), [0,ex(i),ey(i)]); 
end
% MICROSCOPIC BOUNDARY CONDITIONS: INLET (Zou/He BC)
fIn(1,in,liq) = fIn(3,in,liq) + 2/3*rho(:,in,liq).*ux(:,in,liq); % formula of rho at D2Q9 model
fIn(5,in,liq) = fIn(7,in,liq) + 1/2*(fIn(4,in,liq)-fIn(2,in,liq)) + 1/2*rho(:,in,liq).*uy(:,in,liq) + 1/6*rho(:,in,liq).*ux(:,in,liq);
fIn(8,in,liq) = fIn(6,in,liq) + 1/2*(fIn(2,in,liq)-fIn(4,in,liq)) -1/2*rho(:,in,liq).*uy(:,in,liq) + 1/6*rho(:,in,liq).*ux(:,in,liq);
% MICROSCOPIC BOUNDARY CONDITIONS: OUTLET (Zou/He Open BC--second order interpolation scheme)
fIn(3,out,liq)=2*fIn(3,out-1,liq)-fIn(3,out-2,liq); 
fIn(6,out,liq)=2*fIn(6,out-1,liq)-fIn(6,out-2,liq); 
fIn(7,out,liq)=2*fIn(7,out-1,liq)-fIn(7,out-2,liq);
u = reshape(sqrt(ux.^2+uy.^2),lx,ly);
u(bbRegion) = nan;
rho(bbRegion) = nan;
rho_2D=reshape(rho,lx,ly);
p = rho_2D/3;

这一部分代码是LBM核心的计算程序，它的主体结构是一个while循环，当计算精度满足要求时推出循环。在LBM模拟中，也可以采用for循环的模式，人为控制循环次数。进入循环中，首先要通过分布函数的值计算宏观物理量的值:

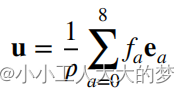
通过公式可以发现，每个格子的宏观物理量仅通过该格子沿9个方向的分布函数即可计算得到，而不需要其周围格子的物理量参与计算。在宏观物理量计算完成后，需要施加宏观边界条件，将边界处的宏观物理量的值指定为应施加的边界条件的值。此处采用的是zou-he进口速度边界条件的形式，详细理论以及推导过程可参阅论文《基于格子 Boltzmann 理论的流场分析》。

至此，该时间步下流场中各格子对应的宏观物理量全部正确。随后，重新根据宏观量计算各格子沿9个方向的平衡分布函数。注意，各格子平衡分布函数的计算也仅涉及到本格子的宏观物理量，其他格子并不参与计算。

随后，对边界格子应用bounce back反弹边界条件。这是一种微观边界条件。微观边界条件是LBM方法中特有的边界条件，其含义是，在对计算域施加边界条件时，不光要对边界上宏观物理量进行处理，还需要对边界上的分布函数也进行特定的操作。该代码中应用的是半步刚性反弹格式，具有二阶精度。具体原理同样可以参考论文《基于格子 Boltzmann 理论的流场分析》。

随后，对分布函数执行迁移操作。使用circshift函数相当于对边界格子上的分布函数执行了周期性边界条件，因此，进口和出口处格子指向流场内部的分布函数是分别从出口和进口处格子的分布函数迁移过来的，是不正确的，因此需要利用zou-he微观边界条件重新计算这些分布函数的值。

至此，该时间步末各格子的分布函数全部正确，继续进入循环参与计算，周而复始，直到流体域达到平衡，计算精度满足要求时停止。

最后，对计算过程进行可视化以及结果的后处理。该部分不作讲解，读者可自行学习。

完整MATLAB代码：

clear
close all
clc
tic
% GENERAL FLOW CONSTANTS
lx = 150; % number of cells in x direction
ly = 50; % number of cells in y direction
uMax = 0.1; % maximum velocity of Poiseuille inflow
Re = 100; % Reynolds number
nu = uMax * ly/ Re; % kinematic viscosity
omega = 1. / (3*nu+1./2.); % relaxation parameter
tPlot = 5; % cycles for graphical output
% D2Q9 LATTICE CONSTANTS
% e6 e2 e5
% \ | / 
% e3-e0-e1 
% / | \ 
% e7 e4 e8 
w = [1/9,1/9,1/9,1/9,1/36,1/36,1/36,1/36,4/9];
ex = [ 1, 0, -1, 0, 1, -1, -1, 1, 0];
ey = [ 0, 1, 0, -1, 1, 1, -1, -1, 0];
opp = [ 3, 4, 1, 2, 7, 8, 5, 6, 9];
liq = [2:(ly-1)]; % liquid part
in = 1; % position of inlet
out = lx; % position of outlet
[y,x] = meshgrid(1:ly,1:lx); % get coordinate of matrix indices
obst = ones(lx,ly); 
obst(1:lx,liq) = 0; % top/bottom boundary
bbRegion = find(obst); % boundary is 1 (use bounce back model)
% INITIAL CONDITION
fIn = reshape( w' * ones(1,lx*ly), 9, lx, ly); % reshape all nodes to a new form (9*lx*ly) matrix
fEq=zeros(9,lx,ly); % initial feq is zero
fOut=zeros(9,lx,ly); % initial ftemporary is zero
avu=0; % initial average velocity is zero
prevavu=0; % next node velocity is zero
% MAIN LOOP (TIME CYCLES)
T=0;
while (1e-9<abs((prevavu-avu)/avu)) || T<20000 % give the restriction of circulation
T=T+1 % start to count
% MACROSCOPIC VARIABLES
rho = sum(fIn); % formula of rho
ux = reshape ( (ex * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho; % formula of velocity
uy = reshape ( (ey * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho; % formula of velocity
% MACROSCOPIC (DIRICHLET) BOUNDARY CONDITIONS
ux(:,in,liq) = uMax; % channel inlet x-velocity 
uy(:,in,liq) = 0; % channel inlet y-velocity 
rho(:,in,liq) = 1 ./ (1-ux(:,in,liq)) .*(sum(fIn([9,2,4],in,liq)) + 2*sum(fIn([3,6,7],in,liq)) ); 
% COLLISION STEP
for i=1:9 
cu = 3*(ex(i)*ux+ey(i)*uy); 
fEq(i,:,:) = rho .* w(i) .* ( 1 + cu + 1/2*(cu.*cu) - 3/2*(ux.^2+uy.^2) );
fOut(i,:,:) = fIn(i,:,:) - omega .* (fIn(i,:,:)-fEq(i,:,:));
end
% MICROSCOPIC BOUNDARY CONDITIONS: NO-SLIP WALLS (bounce-back) 
for i=1:9 
fOut(i,bbRegion) = fIn(opp(i),bbRegion); 
end
% STREAMING STEP 
for i=1:9 
fIn(i,:,: ) = circshift(fOut(i,:,: ), [0,ex(i),ey(i)]); 
end
% MICROSCOPIC BOUNDARY CONDITIONS: INLET (Zou/He BC)
fIn(1,in,liq) = fIn(3,in,liq) + 2/3*rho(:,in,liq).*ux(:,in,liq); % formula of rho at D2Q9 model
fIn(5,in,liq) = fIn(7,in,liq) + 1/2*(fIn(4,in,liq)-fIn(2,in,liq)) + 1/2*rho(:,in,liq).*uy(:,in,liq) + 1/6*rho(:,in,liq).*ux(:,in,liq);
fIn(8,in,liq) = fIn(6,in,liq) + 1/2*(fIn(2,in,liq)-fIn(4,in,liq)) -1/2*rho(:,in,liq).*uy(:,in,liq) + 1/6*rho(:,in,liq).*ux(:,in,liq);
% MICROSCOPIC BOUNDARY CONDITIONS: OUTLET (Zou/He Open BC--second order interpolation scheme)
fIn(3,out,liq)=2*fIn(3,out-1,liq)-fIn(3,out-2,liq); 
fIn(6,out,liq)=2*fIn(6,out-1,liq)-fIn(6,out-2,liq); 
fIn(7,out,liq)=2*fIn(7,out-1,liq)-fIn(7,out-2,liq);
u = reshape(sqrt(ux.^2+uy.^2),lx,ly);
u(bbRegion) = nan;
rho(bbRegion) = nan;
rho_2D=reshape(rho,lx,ly);
p = rho_2D/3;
% VISUALIZATION
if (mod(T,tPlot)==0)
figure(1);
imagesc(rot90(u,1));
colorbar
ti=title('Velocity distribution of the channel','color','k');
set(ti,'fontsize',12);
axis equal off;
drawnow
figure(2);
imagesc(rot90(p,1));
colorbar
ti=title('Pressure distribution of the channel','color','k');
set(ti,'fontsize',12);
axis equal off;
drawnow
end
end
total_T=T
figure(3) 
surf(x,y,u)
ux=reshape(ux,lx,ly);
uy=reshape(uy,lx,ly);
L=(ly-2)/2;
x=-(L-0.5):(L-0.5); 
SIMULATION20=ux(20,2:ly-1)/uMax;
SIMULATION35=ux(35,2:ly-1)/uMax;
SIMULATION55=ux(55,2:ly-1)/uMax;
SIMULATION75=ux(75,2:ly-1)/uMax;
figure(4);
plot(x,SIMULATION20,'ob',x,SIMULATION35,'--dc',x,SIMULATION55,':vm',x,SIMULATION75,'r');
title('Comparison of analytical with LBM results');
xlabel('different location in channel width');
ylabel('u/u_inlet')
legend('Speed at x=20','Speed at x=35','Speed at x=55','Speed at x=75');
toc

小小工人大大的梦
关注
  • 32
    点赞
  • 踩
  • 28
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
深度解析LBM多相流模拟及其Matlab实现：原理与C++代码示例
m0_57781768的博客
06-02 244
格子玻尔兹曼方法（LBM）是一种基于离散速度模型的流体动力学数值方法。与传统的Navier-Stokes方程不同，LBM通过模拟流体微观粒子的运动和碰撞来描述流体的宏观行为。LBM的基本思想源于玻尔兹曼方程，通过离散化和简化，得到适用于计算机模拟的离散速度模型。多相流是指在同一流场中存在两种或两种以上不同相态的流体，这些相态可以是液-液、液-气、液-固或气-固等。多相流的复杂性主要体现在相界面和相间相互作用上。
LBM学习记录1 Introduction
qq_35408950的博客
04-25 957
Lattice Boltzmann Modeling An Introduction for Geoscientists and Engineers学习记录
OpenFOAM——具有压差的平行平板间流动（泊肃叶流动）
asd165654的博客
08-15 1690
本算例翻译整理自：http://the-foam-house5.webnode.es/products/chapter-1-plane-parallel-plates-case/ 这个算例中两平板间没有相对运动，但是沿x方向存在压力梯度（）。针对这个计算，轴线位于两板中间。 连续性方程： 简化x方向的动量方程： 动量方程与艾库特流有些细微的不同，因为在这个算...
LBM程序.rar
05-26
歌字玻尔兹曼方法的程序和书籍和对应的算例和对应的cfd的程序
Python-LBM(格子玻尔兹曼)程序源码实例分析—圆柱绕流篇
热门推荐
weixin_58913471的博客
06-12 1万+
初次学习LBM计算方法，找到一个比较优秀的用python语言编写的圆柱绕流的实例，对每段代码详细添加了注释，帮助自己总结，也为初学者提供一点帮助。 先放一张结果图像：
LBM的源代码
07-01
基于格子Boltzmann方法开源可视化软件的源代码，具有很高的使用价值
关于lbm编程的lbgk
04-18
一个关于lbm的小程序，希望能帮助到到家。也希望大家能多分享~
LBM入门小例子
04-13
一个很好的LBM入门例子，两相流，很容易上手，代码亲试没任何问题
xtnu.zip_LBM_LBM d2q9_数据结构
09-15
标题中的"xtnu.zip_LBM_LBM d2q9_数据结构"暗示了这是一个与Lattice Boltzmann Method（LBM）相关的压缩包，特别是针对二维九速度模型（d2Q9）。LBM是一种数值计算方法，常用于流体力学问题的模拟，包括流体流动、...
LBM-D2Q9-多相流
02-20
D2Q9模型由一个二维的2×2格点构成，每个节点有9个可能的速度方向（上、下、左、右及四个对角线方向），这9种速度对应于Boltzmann方程的9个动量分布函数。 描述中提到的“格子Boltzmann多相流模拟”是指利用LBM来...
泊肃叶流LBM模拟
01-24
LBM方法，基于D2Q9模拟泊肃叶流。模拟结果符合较好。
用LBM模拟泊肃叶流的流动特性，用的fortran
04-18
运用了LBM法模拟泊肃叶流，用的是fortran，详尽，正确，可自行修改参数
lbm_LBM三维_三维LBM_lbm三维_LBM_
09-28
LBM程序设计适合初学者，三维程序不可多得
LBM模拟圆柱绕流
01-25
利用格子Boltzmann方法模拟圆柱绕流的程序，可以供入门者参考。
LBM模拟二维平板流matlab代码
08-07
LBM模拟二维平板发展流的matlab代码，采用D2Q9模型，适合初学者
matlab.zip_LBM_LBM matlab_LBM学习_LBM小程序
09-24
描述中的“学习LBM的小程序,比别的开源软件简单得多”暗示了这个压缩包包含的两个Matlab文件（lbm2.m、lbm1.m）可能是简化版的LBM算法实现，易于理解和使用，适合初学者进行学习和实验。 标签进一步明确了内容的...
2dlbm.rar_2dlbm_LBM
07-14
2dlbm is suitable for learning lbm
LBM（1）——格子玻尔兹曼方法基本介绍
最新发布
weixin_49472580的博客
10-29 3351
在LBM中，流体被建模为由不同速度分量构成的分布函数。通过在每个时间步骤中对这些分布函数进行碰撞和传播操作，LBM模拟了流体的宏观行为，包括速度、密度和压力等。LBM方法的主要优势一方面表现在因其计算尺度而带来的优势——用于计算宏观物理量（密度，速度）的微观物理量（分布函数）是在介观尺度上存在的，因此可以很好地描述一些由于小尺度作用力而产生的现象，如：固液界面接触问题（液滴的表面张力），两相流动问题等。：LBM可模拟流体在多孔介质中的流动，有助于研究地下水流、油藏中的流体行为以及过滤介质中的流体传输。
lbm的d2q9的c语言程序
05-14
LBM (Lattice Boltzmann Method，晶格Boltzmann方法)是计算流体力学(CFD)中的一种数值模拟方法，而d2q9是LBM中使用的晶格类型（二维、速度数为九的晶格）。在实现LBM的过程中，需要用到编程语言来实现算法。 LBM的d2q9的C语言程序，首先需要定义晶格上的各个节点的速度和速度权重。然后，需要定义确定LBM中使用的时间步长和格点大小等参数，以便后续的计算。接着，需要定义求解流体速度、压力和密度的函数，即LBM的核心计算部分。在此基础上，可以定义碰撞和逐步输运的过程，并通过循环进行模拟。最后，输出结果并进行后续的分析和处理。 LBM的d2q9的C语言程序需要考虑多个因素，例如计算效率、精度、稳定性、可读性等方面。因此，在编写程序时需要注意对变量的命名、注释的添加、代码结构的清晰等方面，以便后续的调试和维护。 总之，LBM的d2q9的C语言程序需要综合考虑多方面的因素，才能使得模拟结果更加准确和有意义。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值