本文详细介绍了回归的概念，重点阐述了线性回归的原理，包括线性关系的数学表达、特征向量的扩展、误差处理和似然函数构建。文章还讨论了线性回归的解析解法及其在实际应用中的局限性，对比了解析解与梯度下降法的适用场景。
在正文开始之前，我们先来了解：什么是回归？
非官方版本：各个样本点现在的位置与原始位置相比，发生不同程度的偏离，但最终会回归到原始位置；
官方版本：一般来说，回归是一种研究方法，即先获得一些观测数据，然后根据这些观测数据找到它们背后的规律 ；
这些规律抽象成数学关系，即为：回归方程
如果找到的回归方程是非线性的，则称这个回归过程为非线性回归
这里我们展示一张示例图，让大家更直观感受什么是回归：
一. 情景引入
1.1 示例1
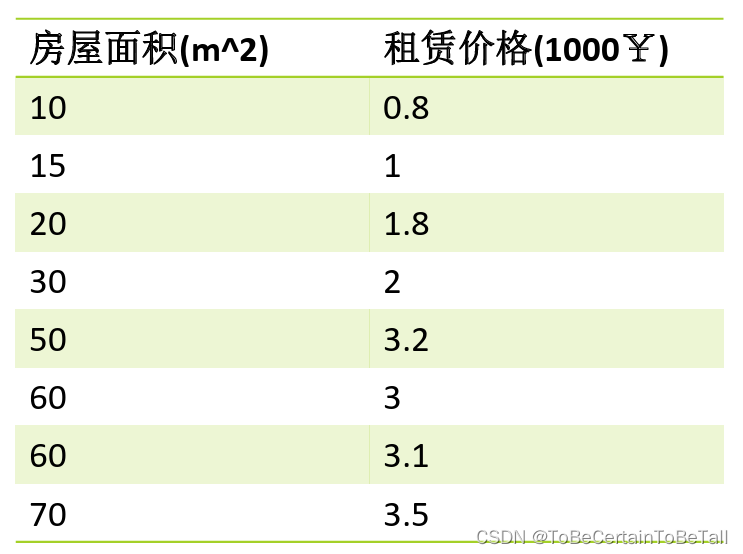
假设我们采集到一个如上的数据集，通过对数据进行分析后得出样本属性值与标签值呈线性增长
那么我们就可以用一条直线来拟合所有的样本点，即
y = a x + b y = ax+b y=ax+b
1.2 示例2
当数据集维度增加时，通过对数据进行分析后，依然可以得出样本属性值与标签值呈线性增长
那么我们就可以用一个平面来拟合所有的样本点，即
h
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
h(x) = \theta _{0} + \theta _{1}x_{1}+\theta _{2}x_{2}
h(x)=θ0+θ1x1+θ2x2
1.3 示例3
当数据集维度再次增加时，通过对数据进行分析后，仍然可以得出样本属性值与标签值呈线性增长
那么我们就可以用一个超平面来拟合所有的样本点，即
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 h(x) = \theta _{0} + \theta _{1}x_{1}+\theta _{2}x_{2}+\theta _{3}x_{3} h(x)=θ0+θ1x1+θ2x2+θ3x3
小节
线性回归是一种监督学习算法，上面所展示的3个示例均属于线性回归问题，其中：每个样本有n个特征，如 x 1 x_{1} x1， x 2 x_{2} x2， x 3 x_{3} x3…
我们将采集到的每个样本的n个特征及其结果记为：
x
1
(
i
)
,
x
2
(
i
)
,
x
3
(
i
)
,
x
4
(
i
)
.
.
.
,
x
N
(
i
)
,
y
(
i
)
x_{1}^{(i)} ,x_{2}^{(i)},x_{3}^{(i)},x_{4}^{(i)}...,x_{N}^{(i)},y_{}^{(i)}
x1(i),x2(i),x3(i),x4(i)...,xN(i),y(i)
基于这样的写法，推广到N维，即M个样本，N个特征的数据集，我们可以记为：
x
1
(
i
)
,
x
2
(
i
)
,
x
3
(
i
)
,
x
4
(
i
)
.
.
.
,
x
N
(
i
)
,
y
(
i
)
（
1
≤
i
≤
M
）
x_{1}^{(i)} ,x_{2}^{(i)},x_{3}^{(i)},x_{4}^{(i)}...,x_{N}^{(i)},y_{}^{(i)} （1\le i \le M）
x1(i),x2(i),x3(i),x4(i)...,xN(i),y(i)（1≤i≤M）
非官方：
i 表示第几个样本
N 表示第几个特征，比如：示例2的第一个特征为房屋面积，第二个特征为房间数量
二. 线性回归 解析解法
结合上面的小节，我们将特征扩展至N维度，就得到：
y = h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ N x N y = h_{\theta } (x) = \theta _{0} + \theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{N}x_{N} y=hθ(x)=θ0+θ1x1+θ2x2+...+θNxN
公式解释1： θ 0 \theta _{0} θ0
这里我们对 θ 0 \theta _{0} θ0这一项进行解释，实际上，我们人为规定了：
x 0 = 1 x_{0}=1 x0=1
首先来聊为什么这样操作：公式写至这一步仅仅是公式推导的开始，我们需要对数据进行更复杂的后续操作；因此， θ 0 \theta _{0} θ0 这个特征格式在数学上应与后面的特征格式保持形式一致
下面我们来解释这样操作后，数据集发生了什么变化：
一般情况下，在数据集原有特征矩阵前加一列全为1的数据
那么我们现在举一反三：只要在原有数据集前加一列相同的数字，公式就可以写为求和公式；因此 x 0 x_{0} x0可以等于任何数，只是一般情况下都为1
= ∑ i = 0 N θ i x i = \sum_{i=0}^{N}\theta _{i}x_{i} =∑i=0Nθixi
= θ T X = \theta^{T}X =θTX
公式解释2： θ T X \theta^{T}X θTX
这里的 θ T \theta^{T} θT为 θ \theta θ列向量进行转置，即变为行向量
[ θ 0 , θ 1 , θ 2 , . . . ] \begin{bmatrix}\theta _{0} ,&\theta _{1},& \theta _{2},& ... \end{bmatrix} [θ0,θ1,θ2,...]
这里的X为 X列向量
[ x 0 x 1 x 2 . . . x N ] \begin{bmatrix} x_{0} \\ x_{1}\\ x_{2}\\ ...\\ x_{N} \end{bmatrix} x0x1x2...xN
根据上述公式，对于每个样本点，都有：
y
(
i
)
=
θ
T
x
(
i
)
+
ϵ
(
i
)
y^{(i)}=\theta ^{T}x^{(i)}+\epsilon ^{(i)}
y(i)=θTx(i)+ϵ(i)
公式解释3： ϵ ( i ) \epsilon ^{(i)} ϵ(i)
公式中 θ T x ( i ) \theta ^{T}x^{(i)} θTx(i) 的结果为预测值，即 y ^ \hat{y} y^
实际上，当我们想要得到标签值y值时，需要再加上一个误差值 ，即 ϵ \epsilon ϵ假定误差 ϵ \epsilon ϵ是独立同分布
服从均值为0，方差为 σ 2 \sigma ^{2} σ2的高斯分布
根据高斯分布的概率密度函数：
p
(
ϵ
(
i
)
)
=
1
2
π
σ
exp
(
−
(
ϵ
(
i
)
)
2
2
σ
2
)
p(\epsilon ^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(\epsilon ^{(i)}) ^{2} }{2\sigma ^{2} })
p(ϵ(i))=2πσ1exp(−2σ2(ϵ(i))2)
将函数
y
(
i
)
y^{(i)}
y(i)带入得到：
p
(
y
(
i
)
∣
x
(
i
)
;
θ
)
=
1
2
π
σ
exp
(
−
(
y
(
i
)
−
θ
T
x
(
i
)
)
2
2
σ
2
)
p(y^{(i)}| x^{(i)};\theta )=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\theta^{T}x^{(i)})^{2} }{2\sigma ^{2} })
p(y(i)∣x(i);θ)=2πσ1exp(−2σ2(y(i)−θTx(i))2)
这样我们就得到了关于
θ
\theta
θ的似然函数：
L
(
θ
)
=
∏
i
=
1
m
1
2
π
σ
exp
(
−
(
y
(
i
)
−
θ
T
x
(
i
)
)
2
2
σ
2
)
L(\theta )=\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\theta^{T}x^{(i)})^{2} }{2\sigma ^{2} })
L(θ)=i=1∏m2πσ1exp(−2σ2(y(i)−θTx(i))2)
对似然函数取对数，并整理：
L ( θ ) = l n L ( θ ) L(\theta )=lnL(\theta) L(θ)=lnL(θ)
= l n ∏ i = 1 m 1 2 π σ exp ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 =ln\prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\theta^{T}x^{(i)})^{2} }{2\sigma ^{2} } =ln∏i=1m2πσ1exp(−2σ2(y(i)−θTx(i))2
= ∑ i = 1 m l n 1 2 π σ exp ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 ) =\sum_{i=1}^{m} ln \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\theta^{T}x^{(i)})^{2} }{2\sigma ^{2} }) =∑i=1mln2πσ1exp(−2σ2(y(i)−θTx(i))2)
= m ∗ l n 1 2 π σ − 1 σ 2 ∗ 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 =m\ast ln\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma ^{2} } \ast \frac{1}{2}\sum_{i=1}^{m}{(y^{(i)}-\theta^{T}x^{(i)})^{2} } =m∗ln2πσ1−σ21∗21∑i=1m(y(i)−θTx(i))2
似然估计的本质可以理解为：求当前某事件出现概率最大时，模型的参数；即 L ( θ ) L(\theta ) L(θ)值最大时， θ \theta θ的取值：
J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 J(\theta)=\frac{1}{2}\sum_{i=1}^{m}{(y^{(i)}-\theta^{T}x^{(i)})^{2} } J(θ)=21∑i=1m(y(i)−θTx(i))2
= 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 =\frac{1}{2}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)} )- y^{(i)})^{2} } =21∑i=1m(hθ(x(i))−y(i))2
= 1 2 ( X θ − y ) T ( X θ − y ) =\frac{1}{2}(X\theta -y)^{T}(X\theta -y) =21(Xθ−y)T(Xθ−y)
= 1 2 ( θ T X T − y T ) ( X θ − y ) =\frac{1}{2}(\theta ^{T} X^{T}-y^{T} )(X\theta -y) =21(θTXT−yT)(Xθ−y)
= 1 2 ( θ T X T X θ − θ T X T y − y T X θ + y T y ) =\frac{1}{2}(\theta ^{T} X^{T}X\theta-\theta ^{T} X^{T}y-y^{T}X\theta +y^{T}y ) =21(θTXTXθ−θTXTy−yTXθ+yTy)
公式解释4： J ( θ ) J(\theta ) J(θ)
这里求 L ( θ ) L(\theta ) L(θ)的最大值等价于求 J ( θ ) J(\theta ) J(θ)的最小值公式第二行换位置： y ^ − y \hat{y} - y y^−y
J ( θ ) J(\theta ) J(θ)是求解线性回归问题的损失函数
对于 J ( θ ) J(\theta ) J(θ)要求其最小值，即
∂ J ( θ ) ∂ θ = 0 \frac{\partial J(\theta )}{\partial \theta } =0 ∂θ∂J(θ)=0
下面就是求导数为0时， θ \theta θ的值：
∂ J ( θ ) ∂ θ = 1 2 ( θ T X T X θ − θ T X T y − y T X θ + y T y ) \frac{\partial J(\theta )}{\partial \theta } =\frac{1}{2}(\theta ^{T} X^{T}X\theta-\theta ^{T} X^{T}y-y^{T}X\theta +y^{T}y ) ∂θ∂J(θ)=21(θTXTXθ−θTXTy−yTXθ+yTy)
= 1 2 ( 2 X T X θ − X T y − ( y T X ) T ) =\frac{1}{2}(2X^{T}X\theta-X^{T}y-(y^{T}X)^{T} ) =21(2XTXθ−XTy−(yTX)T)
= 1 2 ( 2 X T X θ − X T y − X T y ) =\frac{1}{2}(2X^{T}X\theta-X^{T}y-X^{T}y) =21(2XTXθ−XTy−XTy)
= X T X θ − X T y =X^{T}X\theta -X^{T}y =XTXθ−XTy
即：
X
T
X
θ
=
X
T
y
X^{T}X\theta=X^{T}y
XTXθ=XTy
θ
=
(
X
T
X
)
−
1
X
T
y
\theta =(X^{T}X)^{-1}X^{T}y
θ=(XTX)−1XTy
至此，我们算出来
θ
\theta
θ值，即模型的解析解
通过式子可以得出，对于线性回归问题来说，模型的参数只与特征值和标签值有关
非官方的几句话：
解析解评价
1. 对于上面最终可以求得解析解的情况，其实在工业中并不常见
换句话讲，在实际工作中，能解出解析解的情况少之又少
2. 当数据集X非常大时，内存装不下，不通用；
反观梯度下降，可以小批量送入模型，不存在内存放不下的情况；
3. 精度最高：当数据集较小时，可以直接使用
最后，对于解析解，需要补充一点：
存在
X
T
X
X^{T}X
XTX不一定可逆的情况，因此我们需要加入
λ
\lambda
λ扰动，即
θ
=
(
X
T
X
+
λ
I
)
−
1
X
T
y
\theta =(X^{T}X+\lambda I )^{-1}X^{T}y
θ=(XTX+λI)−1XTy
5875
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
